基于NMF的社团及属性标签发现方法
李 真,胡谷雨,潘志松,张艳艳
(陆军工程大学 指挥控制工程学院,南京 210007)
1 引 言
在线社交媒体近年来得到了飞速发展,微博、微信、推特等社交媒体上有大量的用户进行在线交互,从而形成了社交网络.社交网络的一个主要特征是具有社团结构.社团是指一些用户的集合,其中(1)集合内部用户交互紧密而集合之间用户交互稀疏,(2)集合内部用户之间具有较高的相似性而集合之间用户相似性较低[1].社团发现是社交网络分析的重要研究内容,有助于我们理解社交网络的组织结构和功能模块.
目前,研究人员已经提出了多种基于网络拓扑的社团发现方法[2-4].但是,网络拓扑只包含了网络结构方面的信息,并且常常包含噪音[1,5],当网络比较复杂时,仅仅根据拓扑信息无法准确地挖掘出社团.在社交媒体中,除了网络拓扑,还存在许多节点内容信息,如节点属性信息[5-7].例如,在社交网络中可以获得用户的年龄、性别、职业、爱好、购物习惯等信息,这些信息通常称为节点的内容信息[8].节点内容信息描述了节点的一些特性,从而可以度量节点之间的相似性.研究表明,在同一个社团中的节点不仅联系紧密,并且具有相似的特性[8].网络拓扑结构和节点内容信息从不同角度为社团发现提供依据,互为补充,并且这两种信息隐含的社团结构是一致的[5-8].因此,将网络拓扑和节点内容信息结合起来进行分析,可以提高社团发现的准确率[9-12].另一方面,目前的社团发现算法只能挖掘社团结构,但是不能对社团进行语义分析,例如社团的形成原因、社团的功能属性等.对社团进行语义分析使我们不仅能够从结构上理解社团,还能够从行为特性上理解社团,有助于更好地分析、管理社团.节点的内容信息隐含了社团的语义信息,可以利用社团中节点共同的一些属性来对社团进行描述.因此,从节点内容信息中挖掘社团的属性标签具有重要的研究意义.
如何有效地融合两种信息进行社团发现并且对发现的社团进行语义分析是一个具有挑战性的问题.首先,如何将两种信息有效地融合是一个难题.虽然拓扑结构和节点内容隐含了相同的社团结构,但是两种信息都是不全面的、包含噪音的信息,如何融合两种信息来消除噪音的影响而不是叠加噪音是一个难题.其次,如何从节点的内容信息中挖掘社团的语义信息是一个有待解决的问题.用于描述社团的语义信息可以有多种,比如社团的形成原因、社团的功能、社团成员都有的特性等.因此,一个社团可以用多个属性标签来描述,如何挖掘出多个比较准确的属性标签来描述社团是个难题.第三,不同的社团之间存在联系,并且不同社团可能有部分相同的属性标签,即联系紧密的社团应该相应地具有较高的相似度.如何约束通过拓扑挖掘出来的社团关系与通过内容挖掘出来的社团关系的一致性,目前的文献中还没有讨论.
为了解决上述问题,我们提出基于非负矩阵分解(Nonnegative Matrix Factorization,NMF)的社团及属性标签发现方法(Community and Attribute Label Detection,CALD).本文的主要贡献如下:
1)我们提出了一种基于NMF的社团及属性标签发现方法CALD,该方法能够综合利用网络拓扑和节点内容信息同时挖掘社团以及社团的属性标签,有助于更好地理解和分析社团;
2)该方法能够约束从两种信息中挖掘出来的社团结构以及社团间关系的一致性,从而降低噪音的影响,提高社团及其属性标签发现的准确率.
3)在多个真实数据集上的实验结果表明,我们提出的算法可以有效地挖掘社团及其属性标签.
2 相关工作
近年来,通过融合网络拓扑和内容信息进行社团发现得到了比较广泛的关注和研究,该类方法一般被称为多视角聚类[10,11],目前已经有多种算法被提出来.文献[1]提出基于NMF的聚类方法,根据内容信息计算用户相似度、留言相似度和用户交互程度,用于辅助社团发现来提高准确率.文献[9]提出基于semi-NMF的协同聚类方法,根据内容信息计算所有用户之间的相似度,从而得到相似关系图,与拓扑一起用于社团发现.文献[10,11]在基于NMF的聚类框架中,提出了多种正则化项如节点对约束、中心约束、L1范数等约束从不同信息中发现的社团的一致性,提高了社团发现的准确率.文献[12]提出的多视角聚类方法能够在学习过程中自动设置参数的数值,避免了繁复的参数调节问题.在实际情况中,由于用户之间关系的复杂性,不同视角的信息隐含的社团结构和社团数量可能不完全相同,文献[13,14]讨论了这种复杂场景下的多视角聚类问题,允许不同视角的信息隐含不完全相同的社团,提出了更加鲁棒、可扩展性更高的社团发现方法,适应于更加贴近于实际的复杂场景.文献[15]提出首先根据内容信息计算节点之间的相似性,然后将相似性关系与拓扑关系相融合得到新的节点关系图,然后进行社团发现.文献[16,17]通过矩阵分解获得低秩矩阵和稀疏矩阵,其中低秩矩阵表示多个视角共有的数据,稀疏矩阵表示每个视角存在的噪音,最后根据低秩矩阵进行社团发现,从而降低了噪音的影响.文献[18]根据马尔可夫过程对每个视角建立转移矩阵,并求出所有视角公共的低秩转移矩阵,然后对转移矩阵采用谱聚类的方法进行社团发现.文献[19]提出不仅要考虑所有视角共有的信息,还要通过每个视角独有的信息来解决信息缺失的问题.文献中首先对多个视角的数据进行拼接,然后将矩阵分解为低秩的共享信息、稀疏的独有信息和噪音三部分,最后综合利用共享信息和独有信息进行社团发现,提高了社团发现的准确率.但是,上述这些算法主要研究了如何更加有效地综合利用拓扑结构和节点内容信息提高社团发现的准确率,无法对所发现的社团在语义上进行描述.
针对社团进行语义分析的研究目前相对较少.文献[20]研究了如何同时挖掘网络的社团结构和社团的语义描述,提出一个基于NMF的方法,能够利用节点内容信息辅助拓扑信息提高社团发现的准确率,并同时从内容信息中挖掘社团的语义描述信息.文献[21]针对社交媒体上一个用户的所有联系人构成的网络进行研究,提出了一种可以对联系人自动分组的算法.算法综合利用联系人之间的网络拓扑和联系人内容信息进行分组,同时对各个分组中联系人的相似性进行度量,挖掘出联系人共有的一些属性作为分组的属性.

3 基于NMF的社团及属性标签发现方法
在本节中,我们主要介绍基于NMF的社团及属性标签发现算法,其中3.1节给出了模型所需的定义,3.2节描述如何构建优化模型来同时挖掘社团和社团的属性标签,3.3节给出了优化目标的迭代求解方法.
3.1 基本定义
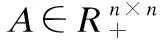
3.2 模型构建
针对网络拓扑结构和节点内容信息,我们采用联合NMF模型,同时挖掘社团指示矩阵U、社团关系指示矩阵S和社团属性矩阵H,实现两种信息的协同学习和有效融合.

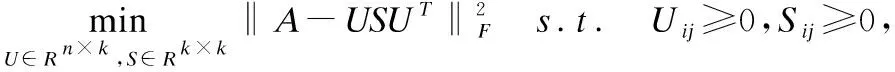
(1)
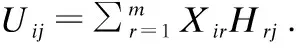
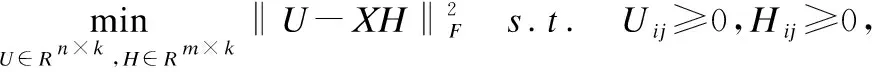
(2)

(3)
综合可得最终的目标函数如下:
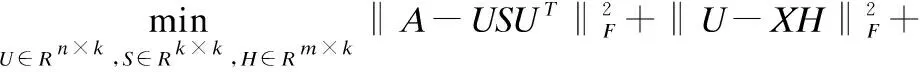
(4)
3.3 优化求解
我们采用梯度下降获得最优解.设γ,λ,ω为拉格朗日乘子来分别约束U≥0,S≥0,H≥0,则拉格朗日函数为:
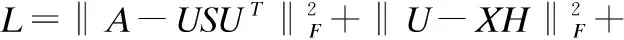
(5)
则可以得到U、S、H的梯度为
(6)
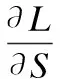
(7)

(8)
由KKT条件可知γijUij=0,λijSij=0,ωijHij=0,则可以得到如下等式:
[-2AUST-2AUS+2USUT(US+UST)+2U-2XH)ijUij-γijUij=0
(9)
[-2UTAU+2UTUSUTU+2(S-HTH)]ijSij-λijSij=0
(10)
[-2XTU+2XTXH-2(HS+HST)+4HHTH]ijHij-ωijHij=0
(11)
则可以得到如下的更新规则:
更新U:固定其他变量,根据式(12)更新U.
(12)
更新S:固定其他变量,根据式(13)更新S.
(13)
更新H:固定其他变量,根据式(14)更新H.
(14)
重复迭代上述矩阵分解过程,并不断更新U、S、H,直至目标函数趋于收敛或达到最大迭代次数.算法流程如下.
算法1.CALD算法
输入:邻接矩阵A和属性矩阵X,社团个数k;
输出:社团指示矩阵U和社团属性矩阵H;
① 初始化U≥0,S≥0,H≥0;
②Whilenot convergentdo
③ 分别根据式(12)、(13)、(14)更新U、S、H;
④Endwhile
3.4 收敛性分析
首先采用辅助函数[22]来证明式(14)的收敛性,辅助函数的定义如下:
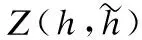
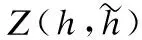
根据上述定义,可以得到目标函数(4)关于H的辅助函数.设J(H)为目标函数(4)中所有包含H的项的和,则J(H)的辅助函数为:
(15)
1http://mlg.ucd.ie/networks
2http://linqs.cs.umd.edu/projects/projects/lbc/
其中Xpq表示矩阵X中第p行和第q列的元素.式(15)是关于H的凸函数,其全局最小值为:
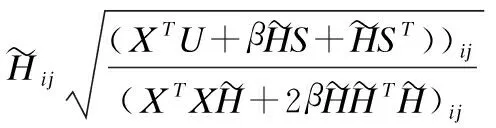
(16)
下面证明当其他变量固定不变时,根据式(14)更新H时,目标函数(4)将单调递减直到收敛.
证明:根据定义1、引理1和J(H)的辅助函数,H的任意k(k≥0)次更新都有:
J(H(k))=Z(H(k),H(k))≥Z(H(k+1),H(k))≥J(H(k+1))
(17)
其中H(k)表示H的第k次迭代.因此可知J(H)是单调递减的.因为目标函数(4)的下界为0,因此H将收敛,由此可证更新式(14)的收敛性.同理可证更新式(12)、(13)的收敛性.
3.5 复杂度分析
4 实验与结果
在本节中,我们在真实网络数据集上进行实验,通过与现有方法进行比较来验证CALD算法的有效性.
4.1 数据集
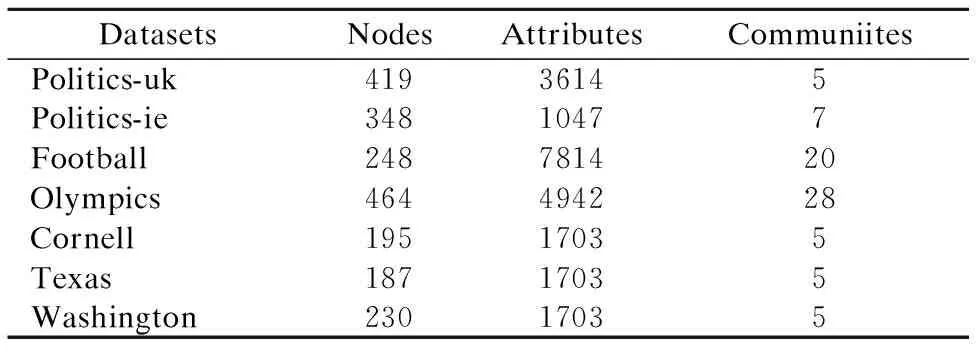
表1 数据集统计数据Table 1 Details of datasets
各个数据集的统计数据如表1所示.其中,前四个数据集1是从Twitter上收集的数据,Politics-uk数据集包含了英国419名政治人员在Twitter上的信息,他们被分为5个社团,分别对应5个政治党派.Politics-ie数据集包含了爱尔兰的348名政治人员的信息,他们被划分为7个社团.Football数据集包含了248名足球运动员的信息,他们分别属于20个足球俱乐部.Olympics数据集包含了2012年伦敦奥运会中28个项目的464名运动员的信息.这些数据集中包含了用户之间的多种交互信息以及多种内容属性信息,我们选用follows和listtext两种信息,其中follows描述了用户之间相互关注的情况,从中可以获得网络拓扑,listtext抽取了用户发布的Tweets的关键词,从中可以获得用户的属性信息.后面3个数据集2分别收集了3个大学的网页信息,共包含了612个网页,每个网页有1703维属性.
4.2 实验和结果
本文中采用的社团发现度量标准为正确率Accuracy[26]和规范化互信息NMI[27](Normalized Mutual Information),这两种度量标准均以真实的社团划分结果为参考,取值范围为0到1,并且取值越高表示发现的社团结构与真实结果越接近,算法性能越好.
本文采用的对比算法有如下5种:PCoSpec (Pairwise Co-regularized Spectral clustering)[28]、CCoSpec(Center-wise Co-regularized Spectral clustering)[28]、PCoNMF (Pairwise Co-regularized NMF clustering)[10]、CCoNMF(Cluster-wise Co-regularized NMF clustering)[10]和SCI(Semantic Community Identification method)[20].其中,PCoSpec和CCoSpec是在谱聚类算法基础上设计的协同聚类算法,分别采用基于节点对和基于中心的正则化项来约束网络拓扑和节点内容隐含的社团指示矩阵的相似性.PCoNMF和CCoNMF利用NMF实现两种数据信息的集成,分别采用节点对和基于中心的约束实现两种社团指示矩阵之间的逼近.SCI基于NMF算法,不仅能够挖掘社团结构,还能够挖掘社团的属性信息.
在本节中,我们在7个真实数据集上进行实验,采用Accuracy和NMI作为社团发现的评价指标,通过与上述5种算法进行对比来验证CALD算法的性能.各个算法在7个数据集上的Accuracy和NMI结果如表2和表3所示.
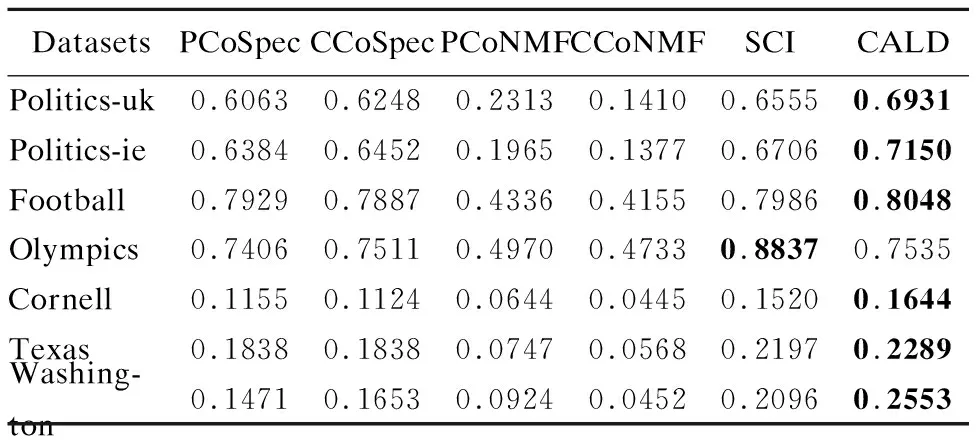
表3 各算法在7个数据集上的NMI结果Table 3 NMI for different methods on seven datasets
从表中可以看到,CALD算法在大部分数据集上具有较高的Accuracy和NMI.例如,在Politics-uk数据集上,CALD算法的Accuracy性能比SCI提高了12%,比CCoNMF算法提高了超过100%.这是由于CALD算法不仅约束两种信息隐含的社团结构的一致性,而且约束社团间关系的一致性,降低了噪音的影响,充分利用了拓扑信息和内容信息,从而有效地提高了社团发现的准确率.另外可以看到在Cornell、Texas、Washington数据集上,各个算法的Accuracy、NMI值都比较低,这是因为这三个数据集所隐含的社团结构比较模糊,导致算法无法比较准确的挖掘出各个社团.
4.3 社团属性标签
在本节中,我们分析通过CALD算法发现的社团属性标签,以Politics-uk数据集为例进行说明.Politics-uk数据集收集了2012年英国419名政治人员在Twitter上的信息,其中listtext中包含了出现频率超过500次的用户Tweets关键词,每个用户都有3614维属性.从数据集的真实社团划分结果可知,所有的用户被划分为五个社团,分别对应保守党、工党、自由民主党、苏格兰民族党及其他党派.

图1 社团属性标签云Fig.1 Word clouds for different communities
图1显示了通过CALD算法挖掘出的保守党、工党和自由民主党的属性标签.其中,单词的大小与社团属性值大小有关,即在社团属性矩阵H中,值越大表示该属性与该社团相关性越高,则在图中的单词也越大.我们去除没有实际意义的单词如“bb”等,每个社团选取最相关的10个属性作为其标签.在没有先验信息的条件下,通过社团发现算法划分完社团之后,并不能确定各个社团对应哪个党派.而CALD算法不仅能够划分出社团,还能够挖掘出各社团的属性标签,从而可以分析社团的语义,有助于判断社团所对应的实际党派.例如,在图1(a)中,可发现“sporting”、“head”、“lead”、“christian”字体较大,因为2012年伦敦举办了奥运会,这体现了当时执政的保守党的工作.图1(b)中的“labour2”′、 “labour3”、“workfare”等清晰地表明该社团是工党,而图1(c)中的“libdemmery”、“libdems2”、“democratic”等则与自由民主党相关.从图中还可以看到不同社团有部分属性相同的标签,例如“candidate2012”同时出现在图1(b)和(c)中,原因可能是这两个党派都参与了2012年的地方议会竞选.不同社团间相同的属性标签越多,表明社团间联系也越多,其关系也越紧密.
5 总 结
社交网络中包含的拓扑信息和内容信息都可以用于挖掘其中隐藏的社团结构.本文针对如何更加有效地利用两种信息来发现社团并分析社团的语义属性展开研究,提出了一种基于NMF的CALD社团及其属性标签挖掘方法.该方法的核心思想是构建一个矩阵联合分解模型,并通过正则化项约束两种信息所隐含的指示矩阵的相似性,从而有效地综合应用拓扑信息和内容信息,提高社团发现的准确率,并挖掘社团的属性标签对社团进行语义描述.实验结果表明,CALD算法能够比较准确地发现网络中的社团,并挖掘出各社团的代表性语义标签,从而加深对社团的属性、功能等的理解.目前,CALD算法的计算复杂度比较高,如何优化算法,提高算法的运行效率是下一步的研究内容.
:
[1] Pei Yu-long,Chakraborty N,Sycara K.Nonnegative Matrix tri-factorization with graph regularization for community detection in social networks[C].International Joint Conference on Artificial Intelligence,2015:2083-2089.
[2] Kuang D,Park H,Ding C H.Symmetric nonnegative matrix factorization for graph clustering[C].SIAM International Conference on Data Mining,2012.
[3] Van Dongen S.A cluster algorithm for graphs[C].Centrum Voor Wiskunde en Informatica,2000.
[4] Shi J,Malik J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):888-905.
[5] Tang L,Liu H.Community detection and mining in social media[M].Morgan and Claypool Publishers,2010.
[6] Tang L,Wang X,Liu H.Uncovering groups via heterogeneous interaction analysis[C].Proceedings of IEEE International Conference on Data Mining,2009:503-512.
[7] Wang N,Chen P,Li X.Community detection in heterogeneous multi-mode social network via Co-training[J].Foundations of Intelligent Systems,2014,277(2014):531-538.
[8] Yang Tian-bao,Rong Jin,Yun Chi,et al.Combining link and content for community detection:a discriminative approach[M].Springer,New York,2014.
[9] Gu Q,Zhou J.Co-clustering on manifolds[C].ACM Knowledge Discovery and Data Mining,2009:359-368.
[10] He X,Kan M Y,Xie P,et al.Comment-based multi-view clustering of web 2.0 items[C].Tthe 23rd International Conference on World Wide Web,2014:771-782.
[11] Tang J,Wang X,Liu H.Integrating social media data for community detection[C].Proceedings of the 2011 International Conference on Modeling and Mining Ubiquitous Social Media,Springer-Verlag,2011:1-20.
[12] Hidru D,Goldenberg A.EquiNMF:graph regularized multiview nonnegative matrix factorization[J].Eprint Arxiv,2014,1409(4018):1-9.
[13] Cheng W,Zhang X,Guo Z,et al.Flexible and robust co-regularized multi-domain graph clustering[C].ACM Knowledge Discovery and Data Mining,2013.
[14] Ni J,Tong H,Fan W,et al.Flexible and robust multi-network clustering[C].ACM Knowledge Discovery and Data Mining,2015.
[15] Ruan Y,Fuhry D,Parthasarathy S.Efficient community detection in large networks using content and links[C].Proceedings of the 22nd International Conference on World Wide Web,2012:1089-1098.
[16] Cheng B,Liu G,Wang J,et al.Multi-task low-rank affinity pursuit for image segmentation[C].IEEE International Conference on Computer Vision,2011.
[17] Guo X,Liu D,Jou B,et al.Robust object co-detection[C].IEEE Conference on Computer Vision and Pattern Recognition,2013.
[18] Xia R,Pan Y,Du L,et al.Robust multi-view spectral clustering via low-rank and sparse decomposition[C].The Association for the Advancement of Artificial Intelligence,2014.
[19] Deng C,Lv Z,Liu W,et al.Multi-view matrix decomposition:a new scheme for exploring discriminative information[C].Proceedings of the 24th International Conference on Artificial Intelligence,AAAI Press,2015.
[20] Xiao W,Di J,Xiaochun C,et al.Semantic community identification in large attribute networks[C].The Association for the Advancement of Artificial Intelligence,2016.
[21] Mcauley J,Leskovec J.Learning to discover social circles in ego networks[C].Advances in Neural Information Processing Systems,2012:539-547.
[22] Daniel D Lee,H Sebastian Seung.Algorithms for non-negative matrix factorization[C].In Advances in Neural Information Processing Systems,2001:556-562.
[23] Fei Wang,Tao Li,et al.Community discovery using nonnegative matrix factorization[J].Data Mining and Knowledge Discovery,2011,22(3):493-521.
[24] Nguyen H T,Dinh T N,Vu T.Community detection in multiplex social networks[C].IEEE Conference on Computer Communications Workshops,IEEE,2015:654-659.
[25] Chris Ding,Tao Li,Wei Peng,et al.Orthogonal nonnegative matrix tri-factorizations for clustering[C].ACM Knowledge Discovery and Data Mining,2006:126-135.
[26] Cheng J,Leng M,Li L,et al.Active semi-supervised community detection based on must-link and cannot-link constraints[J].Plos One,2014,9(10):e110088.
[27] Strehl A,Ghosh J.Cluster ensemble—a knowledge reuse framework for combining multiple partitions[J].J.Mach.Learn,2003,3(3):583-617.
[28] Kumar A,Rai P,Daumé H.Co-regularized multi-view spectral clustering[C].International Conference on Neural Information Processing Systems,2011:1413-1421.

