立即可解网络编码应用于无线网络重传中的时延分析

王 练,彭代渊,陈 巧

(1.西南交通大学 信息科学与技术学院，成都 611756；2.重庆邮电大学 计算机科学与技术学院，重庆 400065)

0 引 言

2000年，Ahlswede等[1]提出了网络编码技术(network coding，NC)，其核心思想是允许网络中间节点对信息进行编码组合并转发，信宿节点可对编码包进行解码。NC的技术特点为无线网络重传提供了新思路，不同信宿节点可根据相同编码包解码出各自丢失数据包，进而提高数据包恢复效率，改善重传性能。基于网络编码思想，Ho等[2]提出了随机线性网络编码(random linear network coding，RLNC)，RLNC编码方式是将数据包进行随机线性组合生成多个线性无关的编码包，当信宿节点收到所有编码包后可进行解码进而得到原始信息，RLNC已被证明是一种能实现最优吞吐量的网络编码机制[3]，但RLNC要求每个信宿节点必须收到足够多编码包后才能恢复原始数据包，导致信宿节点等待解码的时延较大，对于时延敏感的应用场景RLNC并不适用。Katti等[4]则利用异或(exclusive OR,XOR)运算的特点，提出了机会式网络编码(opportunistic network coding，ONC)，与RLNC不同的是，ONC是将多个不同的数据包进行XOR运算从而生成编码包，如果某个信宿节点只丢失该编码包集合中的某一数据包，则该信宿节点能对编码包解码并恢复丢包，信宿节点不需等待所有编码包到达就能恢复丢失数据包，因而等待解码所需的时延相比RLNC少。

随着无线网络的发展，基于无线网络的实时应用被广泛使用，例如实时多播服务、车联网中道路单元与汽车之间的实时安全信息、传感网络中节点之间的实时信息传输等。针对实时应用，文献[5-6]首先考虑了基于网络编码重传中的时延问题，并提出了立即可解网络编码(instantly decodable network coding，IDNC)思想，IDNC已作为网络编码的一个子类问题被广泛研究。按照编码条件不同，IDNC思想分为2类，第1类是狭义立即可解网络编码(strict instantly decodable network coding， S-IDNC)[5-6]，S-IDNC编码条件苛刻，要求生成的编码包在其所有目标信宿节点都能立即解码。第2类是广义立即可解网络编码(generalized instantly decodable network coding，G-IDNC)[7]，不同于 S-IDNC的是，G-IDNC的编码条件不限制编码包的即时可解性，信宿节点可将不可解编码包直接丢 弃，G-IDNC对数据包的编码机会利用率更高，满足编码条件的编码包更多，但编码包生成过程的复杂度也更大。 S-IDNC和G-IDNC都利用机会式网络编码思想，使用XOR运算进行编解码操作，编解码简单。文献[8-11]具体研究了IDNC问题中最小化完成时延问题，文献[12-13]研究了IDNC问题中最小化解码时延问题，文献[14-15]则分析了完成时间和解码时延折中的问题。

为比较S-IDNC和G-IDNC的时延性能差异。本文针对无线单跳网络广播场景，在考虑信宿节点丢包率情况下，分别提出2种IDNC加权算法，并以所提算法为支撑,间接比较S-IDNC和G-IDNC在信宿节点的平均解码时延、信宿节点平均完成时延、系统完成时延和信宿节点完成时延大小分布上的差异。以期所得结论为基于IDNC在无线网络重传中应用选择提供参考。

1 系统模型和参数

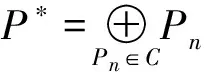
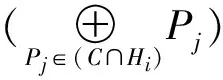
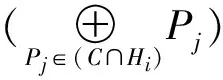
3)无效编码包。集合C不包含Ri丢失的数据包，即C∩Wi=∅，则P*在Ri处无效。

(1)

(2)

在IDNC问题研究中，数据包之间的编码关系用IDNC图刻画，图1给出了S-IDNC和G-IDNC图。对于S-IDNC编码思想，要求生成的编码包P*在Ri(i∈{1,2,…,M})处是立即可解或无效，其IDNC图用GS-IDNC(v,ε)表示，顶点vi表示一个丢包Pi∈L，L表示丢失包集合，满足L=W1∪W2∪…∪WM，边εi,j表示满足S-IDNC编码条件的一个二元编码包，图1a中任意一个团则表示一个多元S-IDNC编码包。顶点vi和vj之间存在边εi,j∈ε必须满足条件1。

条件1在任何信宿节点，vi和vj所对应数据包Pi和Pj都不同时丢失，称Pi和Pj满足结合关系，否则为互斥关系。

例1：图1a中状态矩阵对应的GS-IDNC(v,ε)如表1所示。

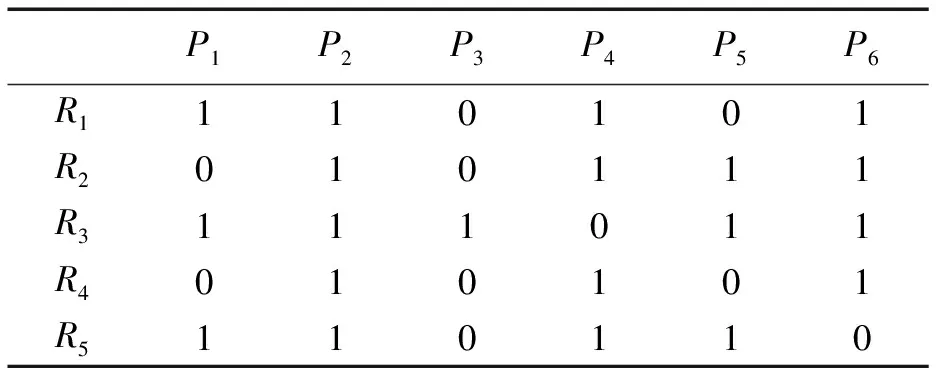
表1 状态矩阵Tab.1 System matrix

0表示丢包，1表示接收

图1a中顶点v1和v4之间存在一条边，表明P*=P1⊕P4满足S-IDNC编码条件的二元编码包，P*在P1目标信宿节点R2，R4和P4目标信宿节点R3处都立即可解，R2和R4由P4⊕(P1⊕P4)解码出P1，R3由P1⊕(P1⊕P4)解码出P4。v4，v5和v6以及之间的边组成一个团，则表明P*=P4⊕P5⊕P6满足S-IDNC编码条件的多元编码包。

G-IDNC允许编码包在某些信宿节点不可解，对应IDNC图用GG-IDNC(v,ε)表示，顶点vi,j表示数据包Pj∈Wi，顶点vi,j和vk,l之间存在一条边εi,j;k,l∈ε则必须满足条件2或条件3。

条件2j=l，Ri和Rk丢失相同的数据包Pj=Pl。

条件3当Pj∈Wi且Pl∈Wk时，有Pj∈Hk且Pl∈Hi。

GG-IDNC(v,ε)中的任意一条边εi,j;k,l表示编码包Pj⊕Pl在Ri和Rk处是立即可解的。表1所示的状态矩阵所对应的GG-IDNC(v,ε)如图1b所示，顶点v1,5和v2,1之间存在一条边，即编码包P1⊕P5在R1和R2处可以立即解码，尽管P1⊕P5在R4处不可解，但G-IDNC允许这种情况，这也是G-IDNC区别于S-IDNC的地方。由图1a和图1b对比可知,GG-IDNC(v,ε)的复杂度高于GS-IDNC(v,ε)，G-IDNC刻画的编码关系更为详细。

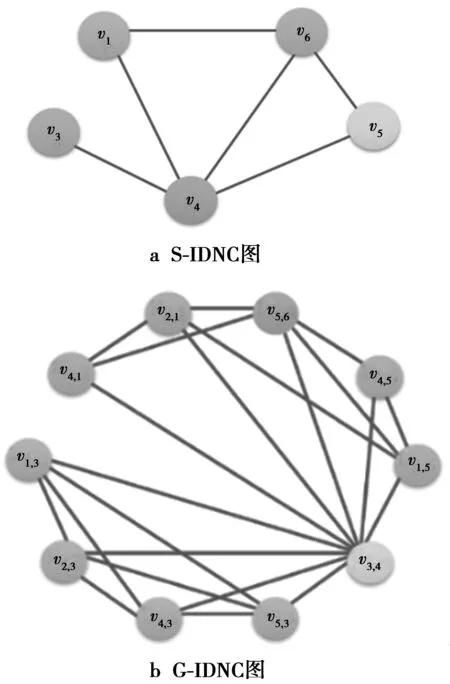
图1 S-IDNC图和G-IDNC图Fig.1 S-IDNC graph and G-IDNC graph

2 基于IDNC的最大权重团算法

2.1 时延问题描述

基于立即可解网络编码的重传思想对时延要求较高，时延分为完成时延和解码时延，完成时延指恢复所有丢包系统所经历的重传次数[8]，文献[7]给出了解码时延定义，是指编码包P*在某个丢包信宿节点Ri处是不可解或无效的，则Ri会产生一个单位的解码时延，该定义没考虑编码包丢失的情况，忽略了链路丢包率对时延的影响，本文在该定义基础上，对解码时延定义进行扩展。

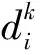
(3)

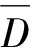
(4)

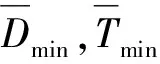
(5)

(6)

(7)

以上分析可知，信宿节点完成时延由其解码时延和丢失数据包集合大小|Wi|决定，初始传输后|Wi|已确定，因而本文从解码时延角度分析时延问题。

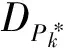
(8)

(8)式中，pi表示信宿节点Ri的丢包率。由(2)式、(8)式可得

(9)

用LR表示有丢包的信宿节点集合，则(9)式满足

(10)

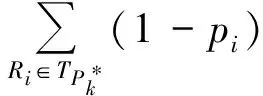
(11)

2.2 相关定理

(12)

定理1得证。

(13)

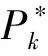
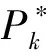
综合1)，2)可知定理2得证。

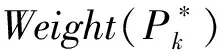
(14)

2.3 算法设计

利用启发式算法把寻找最大权重编码包问题转化为IDNC权重图中寻找最大权重团问题，S-IDNC权重图和G-IDNC权重图定义分别如下。

S-IDNC权重图GS-IDNC(ν,ε,ω) 在GS-IDNC(ν,ε)中增加顶点权重值ω，顶点vi的权重ωi计算方式如下。

1)用ai,j表示S-IDNC图中2个顶点vi和vj的连接关系，若vi和vj相连，有ai,j=1，否则ai,j=0；

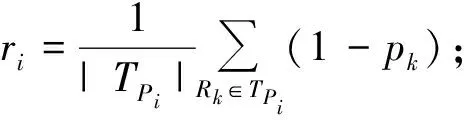
4)顶点权重定义为ωi=rici。

G-IDNC权重图GG-IDNC(ν,ε,ω) 在GG-IDNC(ν,ε)中增加顶点权重值ω，顶点vi,j的权重ωi,j的计算方式如下：

1)定义ai,j;k,l表示顶点vi,j和vk,l的连接关系，若vi,j和vk,l之间存在一条边，有ai,j;k,l=1，否则ai,j;k,l=0；

2)定义接收权重ri,j表示数据包Pj在信宿节点Ri被成功接收的概率期望值，有ri,j=1-pi；

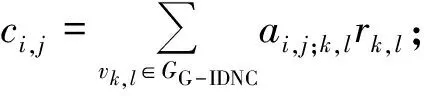
4)顶点权重定义为ωi,j=ri,jci,j。

基于以上分析以及IDNC权重图定义，提出2种数据包选择算法生成S-IDNC编码包和G-IDNC编码包，分别为S-IDNC带权重顶点搜索算法(weighted search algorithm for S-IDNC，WSAS)和G-IDNC带权重顶点搜索算法(weighted search algorithm for G-IDNC，WSAG)。2种算法在执行的过程中都会更新权重图，更新方式是删除与当前权重最大顶点不相连的顶点以及边。算法伪代码如下。

WSAS算法生成S-IDNC编码包。

输入：Ω//状态矩阵

1：初始化：CS-IDNC=∅ //编码数据包集合

2：if |TPk|=|LR|

3：P*=Pk

4：else

5： GenerateGS-IDNC(v,ε,ω)

6： while (ε≠∅)

8：CS-IDNC=CS-IDNC∪Pmax//Pmax→CS-IDNC

9： updatesGS-IDNC(v,ε,ω)

10：end while

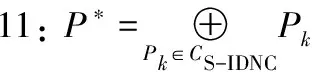
12：end if

13：transmitP*

14：all receivers decodeP*

15：SupdatesΩ

16：Repeat the above steps until all lost packets recovered.

WSAG算法生成G-IDNC编码包。

输入：Ω//状态矩阵

1：初始化：CG-IDNC=∅ //编码数据包集合

2：if |TPk|=|LR|

3：P*=Pk

4：else

5： GenerateGG-IDNC(v,ε,ω)

6： while (ε≠∅)

8：CG-IDNC=CG-IDNC∪Pmax//Pmax→CG-IDNC

9： updatesGG-IDNC(v,ε,ω)

10：end while

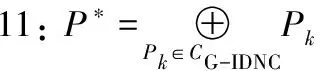
12：end if

13：transmitP*

14：all receivers decodeP*

15：SupdatesΩ

16：Repeat the above steps until all lost packets recovered.

2.4 计算复杂度

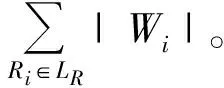
综上，2种算法的计算复杂度都由IDNC权重图构建情况决定，2种算法的计算复杂度对比如表2所示。

表2 计算复杂度Tab.2 Computation complexity

3 仿真实验与分析

本节对所提WSAS和WSAG算法进行时延性能仿真，并同文献[6]中的算法Algorithm_1，ARQ重传算法，以及理想情况下性能值进行比较。理想情况下的性能值用Lower表示，其对应的信宿节点平均解码时延、信宿节点平均完成时延和系统完成时延理想性能值大小已在(5)式、(6)式和(7)式中给出。仿真平台为MATLAB 2014a，比较的时延性能有信宿节点平均解码时延，信宿节点平均完成时延和系统完成时延，同时也比较了WSAS和WSAG在信宿节点处的时延大小分布。通过比较WSAS和WSAG的重传性能，间接比较S-IDNC和G-IDNC 2种编码思想的区别。本文进行以下2个实验。

实验1测试信宿节点数对时延性能影响。数据包数N=40，信宿节点丢包率pi(0≤pi≤0.4)，信宿节点数M从10增加到100，每次递增10，图2给出了实验结果，其中，图2d和图2e分别表示信宿节点在不同情况下的完成时延大小分布。

由图2a和图2b对比可以看出，信宿节点平均完成时延和平均解码时延的变化趋势相同，这间接证明了信宿节点完成时延大小由其解码时延以及丢失数据包数决定，完成时延大小的变化由解码时延大小的变化决定。随着信宿节点数增加，WSAS，WSAG和Algorithm_1的时延性能都逐渐变差，因为随着M增加，相同数据包在更多信宿节点丢失，数据包丢失分布更密集，编码机会减少，最后导致基于网络编码重传机制的重传性能下降。WSAG在平均解码时延和平均完成时延上都要优于对比算法，系统完成时延却高于Algorithm_1和WSAS。进一步，由图2d和图2e可看出，WSAS的信宿节点完成时延大小分布相对较集中，且时延值较大，但信宿节点的完成时延最大值小于WSAG的完成时延最大值，与图2c所反映结果相同；WSAG的信宿节点完成时延大小分布更为分散，完成时延均值优于WSAS的，与图2b所反映结果相同。

实验2测试数据包数对时延性能的影响。信宿节点M=40，数据包数N从10变化到100，每次递增10，图3给出了实验结果。

由图3可以看出，随着数据包数增加，算法时延性能值都逐渐增大，因为在信宿节点数和丢包率不变情况下，数据包数N增加必然导致每个信宿节点丢失数据包更多，最后导致解码时延均值、完成时延均值和系统完成时延都增加。WSAS和WSAG时延性能都比较好，因为数据包数增加，数据包丢失分布越分散，数据包之间结合性越好，编码机会更多。

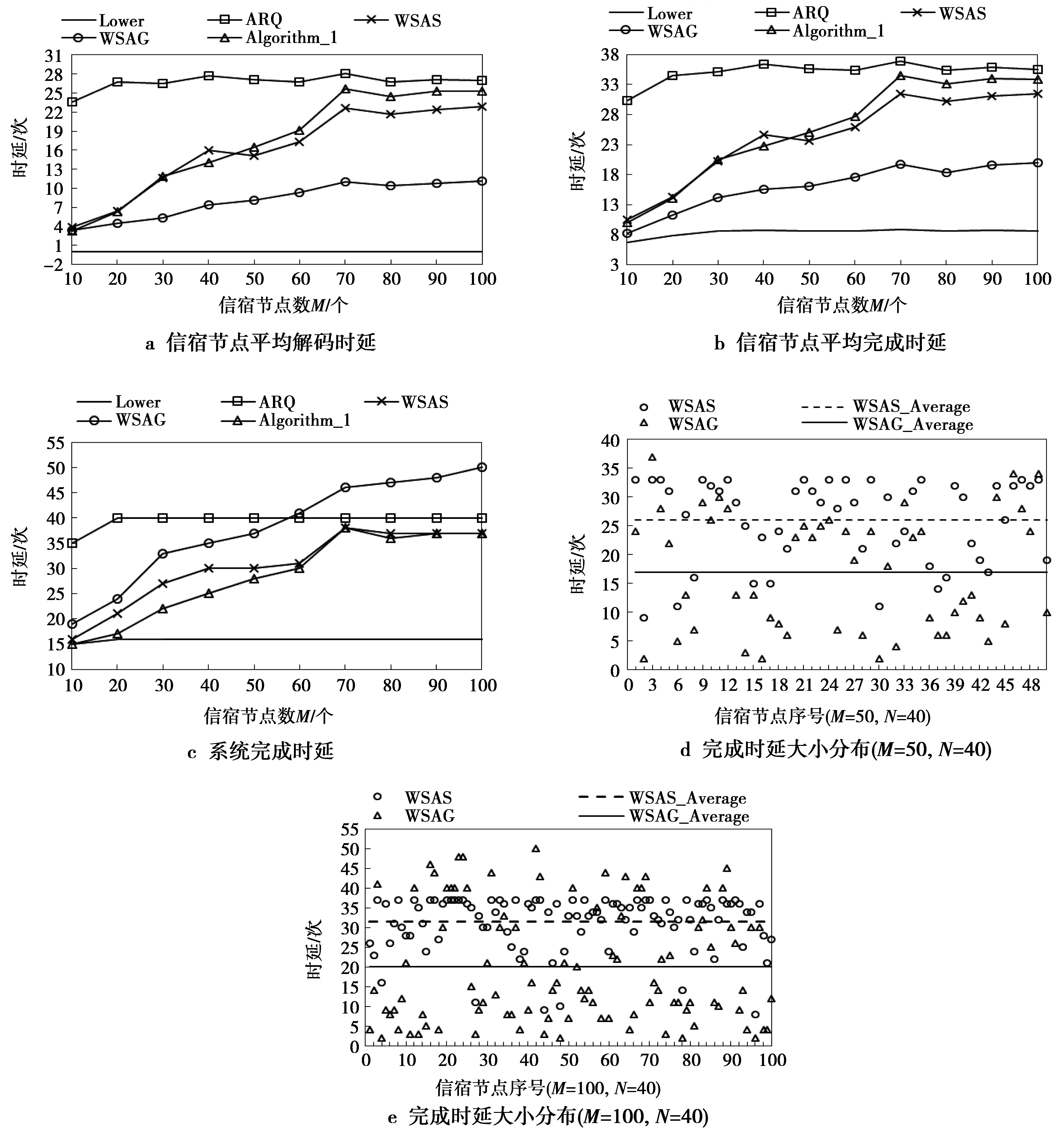
图2 信宿节点数对时延性能的影响 (N=40)Fig.2 Transmission performance versus the number of receivers(N=40)

WSAS和WSAG分别是S-IDNC和G-IDNC编码思想体现，以上分析间接比较了S-IDNC和G-IDNC在重传时延性能上的区别，综合以上分析结果可得以下结论。

1)G-IDNC编码方案在信宿节点平均解码时延和平均完成时延上要优于S-IDNC编码方案。

2)G-IDNC编码方案的系统完成时延要高于S-IDNC编码方案。

3)G-IDNC编码方案使得信宿节点的时延(解码时延和完成时延)大小分布比较分散，S-IDNC的时延大小分布较为集中。

4)平均完成时延、平均解码时延和系统完成时延都受信宿节点丢包分布情况影响，丢包分布越分散，数据包之间的可结合性越好，基于IDNC重传方案在重传性能上表现越好。

4 结束语

本文分析了S-IDNC和G-IDNC这2种典型的IDNC编码思想，并针对这2种思想分别提出了2种IDNC重传算法WSAS和WSAG，为使每次重传的编码包在信宿节点处产生解码时延最小，2种算法都将数据包选择问题转换为IDNC权重图中选择最大权重团问题。通过实验对比了WSAS和WSAG的重传时延性能，结果表明WSAS和WSAG都能有效改善重传性能。同时，以实验结果间接分析了S-IDNC和G-IDNC的差异，基于G-IDNC重传方案在信宿节点完成时延均值和解码时延均值上要优于基于S-IDNC的重传方案，但前者在系统完成时延上要弱于后者；基于S-IDNC和G-IDNC的重传方案都不能在信宿节点时延均值和系统完成时延上同时达到最优。

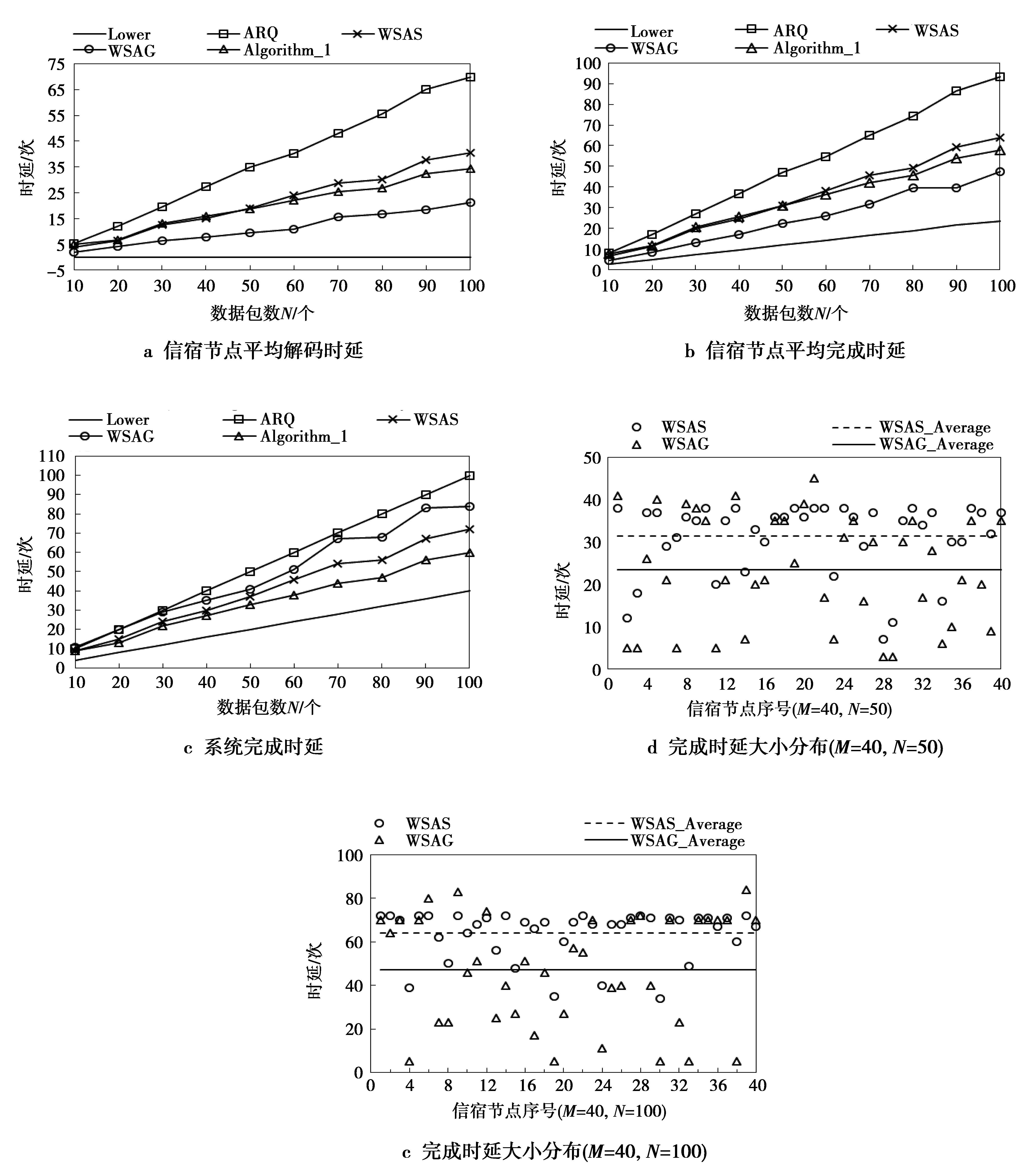
图3 数据包数对时延性能的影响(M=40)Fig.3 Transmission performance versus the number of packets(M=40)

参考文献：

[1] AHLSWEDE R, CAI N, LI S Y R, et al. Network information flow[J]. Information Theory, IEEE Transactions on, 2000, 46(4): 1204-1216.

[2] HO T, MÉDARD M, KOETTER R, et al. A random linear network coding approach to multicast[J]. IEEE Transactions on Information Theory, 2006, 52(10): 4413-4430.

[3] ERYILMAZ A, OZDAGLAR A, MÉDARD M, et al. On the delay and throughput gains of coding in unreliable networks[J]. IEEE Transactions on Information Theory, 2008, 54(12): 5511-5524.

[4] KATTI S, RAHUL H, HU W, et al. XORs in the air: practical wireless network coding[J]. ACM SIGCOMM Computer Communication Review, 2006, 36(4): 243-254.

[5] SADEGHI P, TRASKOV D, KOETTER R. Adaptive network coding for broadcast channels[C]//Proc. 5th Workshop on Network Coding, Theory and Applications. New York: IEEE Press, 2009: 80-86.

[6] SADEGHI P, SHAMS R, TRASKOV D. An optimal adaptive network coding scheme for minimizing decoding delay in broadcast erasure channels[J]. EURASIP Journal on Wireless Communications and Networking, 2010(1): 1.

[7] SOROUR S, VALAEE S. Minimum Broadcast Decoding Delay for Generalized Instantly Decodable Network Coding[C]//IEEE Global Telecommunications Conference. New Youk: IEEE Press, 2010:1-5.

[8] SOROUR S, VALAEE S. On Minimizing Broadcast Completion Delay for Instantly Decodable Network Coding[C]//IEEE International Conference on Communications. New York: IEEE Press, 2010:1-5.

[9] SOROUR S, DOUIK A, VALAEE S, et al. Partially blind instantly decodable network codes for lossy feedback environment[J]. IEEE Transactions on Wireless Communications, 2014, 13(9): 4871-4883.

[10] LE A, TEHRANI A S, DIMAKIS A G, et al. Instantly decodable network codes for real-time applications[C]//2013 international symposium on network coding (NetCod). New York: IEEE Press, 2013: 1-6.

[11] SOROUR S, VALAEE S. Completion delay minimization for instantly decodable network codes[J]. IEEE/ACM Transactions on Networking (TON), 2015, 23(5): 1553-1567.

[12] DOUIK A, SOROUR S, Al-NAFFOURI T Y, et al. A lossy graph model for delay reduction in generalized instantly decodable network coding[J]. IEEE Wireless Communications Letters, 2014, 3(3): 281-284.

[13] ZHAN C, XIAO F. Coding based wireless broadcast scheduling in real time applications[J]. Journal of Network and Computer Applications, 2016, 64: 194-203.

[14] YU M, ABOUTORAB N, SADEGHI P. From instantly decodable to random linear network coded broadcast[J]. IEEE Transactions on Communications, 2014, 62(11): 3943-3955.

[15] ABOUTORAB N, SADEGHI P, SOROUR S. Enabling a tradeoff between completion time and decoding delay in instantly decodable network coded systems[J]. IEEE Transactions on Communications, 2014, 62(4): 1296-1309.