基于实数遗传算法与神经网络的农机总动力预测及分析

任永泰，张 达，许东阳，乔金友

(东北农业大学 a.理学院；b.工程学院，哈尔滨 150030)

0 引言

农业机械化的发展有利于减少农村劳动力需求，提高农业生产率，而农机总动力是衡量农业机械化水平的主要指标，也是制定农业发展规划的有力依据。因此，精确预测农机总动力的发展趋势，对指导产业结构调整与农业机械化协调发展具有深远意义。农业机械总动力是指用于农、林、副、渔的机械总动力之和,具体包括拖拉机及配套农具、农业排灌动力机械、联合收割机、机动脱粒机，以及渔用机动船等机械动力之和[1-4]。目前,对农机总动力进行预测的方法主要有移动平均、灰色GM(1,1)模型、指数平滑、线性回归、曲线拟合、线性组合预测及标准BP神经网络等预测模型。这些方法各有其优点和不足,所得的结果也存在差异[5-14]。选取较好的阈值可以提高神经网络效率[15-16]，本文采用实数遗传算法来优化神经网络的阈值，从而提高神经网络对农机总动力预测的速度和精度。为此，依据黑龙江省1983-2014年农机总动力数据[17]，运用实数遗传算法训练神经网络对黑龙江省农机总动力进行拟合和预测。

1 基本理论

1.1 遗传算法简介

1.1.1 初始种群的产生

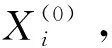
(1)

令rij为与第i个初始个体的第j个分量对应的在[0,1]区间内服从均匀分布的随机数[18]，初始种群按下式产生，即

(2)

其中，

1.1.2 个体适应度的计算

本文在基于序的基础上构造适应度函数，先将种群中的所有个体按照目标函数值的好坏进行依次排列，设参数β∈(0,1)，定义基于序的适应度函数为eval(Xi),则

eval(Xi)=β(1-β)i-1，i=1,2,…,m

(3)

其中，Xi为种群个体按优劣排序后i个个体，β∈(0,1)，一般在0.01～0.3之间。

1.1.3 选择配对

由链式法则，如初始种群的规模m为偶数，则先将其分为两组，第1组包括前m/2个个体，第2组包括后m/2个个体。首先选取第1组第1个个体，然后再与第2组中采用轮盘赌选择法随机选取的1个个体进行配对，再选取第1组第2个个体，然后再与第2组中剩下的(m/2)-1个个体中采用轮盘赌选择法随机选取的1个个体进行配对，按照这样的方法可以得到m/2对个体。

如初始种群的规模m为奇数，在分组时让第1组比第2组少1个个体，按照偶数时的配对方法产生(m-1)/2对个体，然后再将第2组剩下的1个个体与第1组的第1个个体配对。

1.1.4 子代个体的产生

(4)

(5)

其中，λ为映射系数，一般取大于1的数[19]。

1.1.5 变异

步长的选择一般视具体情况而定，较小的步长成功的可能性较大，但有时较大的步长会有较快的效率，一般采用如下变异算子，即

x'=x±0.5LΔ

(6)

该变异操作方法步长的选择应根据具体问题所要达到的优化效果来确定[20]，在优化过程中步长既可以固定不变有时又可以改变。

1.1.6 进化的终止条件

每进化一次计算一下每个个体的目标值，当相邻的两次进化平均目标值之差小于等于某个给定的精度ε时，即满足下式条件即可终止进化[21]，有

|F(X(t+1))-F(X(t))|≤ε

(7)

其中，F(X(t+1))为第t+1次进化后种群的平均目标值；F(X(t))为第t次进化后种群的平均目标值。

1.2 BP神经网络

BP神经网络(Back Propagation Neural Network)是一种多层前馈型神经网络[22]，第一层为输入层，神经元的个数等于输入数据的维数；最后一层是输出层，对输入信号作出响应；中间各层是隐含层，可以是1层也可以是多层。BP神经网络的训练过程一般分为两个部分：一个是输入信号的正向传递；另一个是误差信号的反向传递。

在信号的正向传播阶段，由输入层神经元接收输入信号，经各隐含层神经元传递和处理后，传向输出层神经元，输出层神经元进行最后的处理得到实际输出，并计算实际输出与期望输出之间的误差[23]。

正向信号的计算过程大致描述如下：输入层各个神经元的线性加权加上阈值作为下一个神经元的输入，经过激励函数的转化后输出，作为输出层的输入。假设输入层有n个神经元，隐层有h个神经元，输出层m个神经元，假设某一个输入信号为X=[x1,x2,…,xn]T，输入层第i个神经元与第j个隐层神经元的连接权值为wij，那么第j个隐层神经元的输入为uj，它的阈值为bj，激励函数为f(·)，第j个隐层神经元输出yj的计算方法为[24]

(8)

(9)

第j个隐层神经元的输出又作为输出层的输入信号，输出层的作用原理与隐含层相同，在依照上述步骤计算出输出信号的值。在误差的反向传递阶段，误差由输出层传向隐含层，计算误差对隐含层与输出层之间的连接权值和阈值的偏导数，修正权值和阈值，接着误差由隐含层传向输入层，计算误差对输入层与隐含层之间的连接权值和阈值；修正权值和阈值，并进行下一次的信号正向传播。完成一次输入信号正向传播和一次误差信号反向传递也就完成了一次网络迭代，迭代过程周而复始的进行也就是权值不断调整的过程。该过程一直进行下去，直到误差达到精度要求为止，或者网络满足预先设定的其他停止条件。

2 实例分析

分别运用标准BP训练算法和实数遗传算法训练神经网络来预测黑龙江省农机总动力的发展变化，表1数据是1983-2014年黑龙江省农机总动力，来自国家统计局官方网站。

首先对表1中原始数据(观测值)进行归一化处理，其表达式为

(10)

预测结果如表1所示。从算法上来看，采用标准BP算法来训练神经网络，BP神经网络的结构为标准3层结构，网络输出结点的个数为4，隐含层神经元的个数为6，输出神经元的个数为1。当训练次数为266 308次时，耗时6 352.4s，均方误差为0.018%。采用实数遗传算法训练BP神经网络，结构同为标准3层结构，网络输出结点的个数为4，隐含层神经元的个数为6，输出神经元的个数为1，均方误差仅为0.001 2%。由此可知，在算法的总体进程中用实属遗传算法训练神经网络在运算速度上有更大的优势。

表1 原始数据及预测结果

续表1 万kW

从农机总动力预测整体效果可以得出：在离农机总动力需要预测年份越近的时期(2005-2014年)，用实数遗传算法训练的神经网络预测的农机总动力越来越准确。所以，2017年和2018年的农机总动力预测结果将会更准确。该预测结果可以为黑龙江省制定政策提供如下的理论参考。

1)预测结果可为黑龙江省的农业机械化发展趋势和农机产品市场分析等方面提供理论指导，也可以从“供给侧”对农机总动力进行调节，使其既能在不浪费资源配置的同时满足实际需求，将剩余的资源合理配置到其他领域，提高社会资源的有效利用。

2)黑龙江省是我国的农业大省，制定农业机械化发展规划和预测近阶段农业机械化发展水平是当前政府部门必须提前进行的工作[25]，而预测结果可以为政府相关部门提供农业结构变化和农业发展水平的参考依据。

3)预测结果使政府能够观察到农业机械化的发展趋势，提前做好资源的有效配置，尤其随着农业机械化和现代化的不断深化。农村人口中剩余劳动力在不断的增加[26]，解决好这些剩余资源不仅可以提升社会整体发展水平，也能够增加农村的经济的快速发展。

4)预测结果能够给政府工作报告提供参考，使财政预算分配更为合理[27]，科学的制定农机补贴率、补贴范围、补贴标准等指标[28-30]。

5)预测结果可以作为构建新型农村和政府加快土地流转和农村合作社的建设提供参考依据，可为农业产出量、农民收入水平的状况[31]提供参考对照。

3 结论

从提高黑龙江省农机总动力预测精度出发，为能够更好地确定黑龙江省农机总动力带来的影响，依据黑龙江省1983-2014年农机总动力数据，用实数遗传算法训练神经网络对黑龙江省2014-2018年农机总动力进行预测。预测结果表明：实数遗传算法训练的神经网络与标准BP神经网络的预测相比，具有较好的预测性能。同时，以此结果为黑龙江省的农业机械化发展趋势、农机产品市场需求、农村剩余劳动力资源有效配置等方面给出了发展建议。

参考文献：

[1] 杨敏丽. 我国农业机械化发展的阶段性[J].中国农业大学学报,1998(4):11-15.

[2] 易金根, 沈广树.江苏省农业机械化现状及发展对策[J].南京农业大学学报,1998, 21(3):116-120.

[3] 杨敏丽,白人朴.农业机械总动力与影响因素关系分析[J].农机化研究,2004(6):45-47.

[4] 鞠金艳,赵林,王金峰.农机总动力增长波动影响因素分析[J].农业工程学报,2016(2):84-91.

[5] 宋珲,董欣,王兵.基于BP神经网络的农机总动力预测模型研究[J].东北农业大学学报,2009(4):116-120.

[6] 王黎明, 赵清华.黑龙江省农机总动力灰色预测与分析[J].农机化研究,2003(2):48-49.

[7] 谢红梅, 周清, 黄大明,等.2001年-2010年广西农机总动力人工神经网络预测[J].广西科技大学学报,2001, 12(4):26-28.

[8] 朱荣胜, 王福林.黑龙江省农机总动力趋势包络预测与分析[J].东北农业大学学报,2006, 37(4):512-515.

[9] 鞠金艳,王金武,王金峰.基于BP神经网络的农机总动力组合预测方法[J].农业机械学报,2010(6):87-92.

[10] 赖庆辉, 米伯林, 杨志坚.基于人工神经网络的黑龙江省农机总动力预测[J].农机化研究, 2005(4):272-274.

[11] 关凯书, 张丽, 张美华,等.我国农机总动力需求的模糊神经网络预测模型[J].农业机械学报,1999, 30(5):86-88.

[12] 朱瑞祥, 黄玉祥, 杨晓辉.用灰色神经网络组合模型预测农机总动力发展[J].农业工程学报,2006, 22(2):107-110.

[13] 张淑娟, 赵飞.基于Shapley值的农机总动力组合预测方法[J].农业机械学报,2008, 39(5):60-64.

[14] 邱立春, 崔国才, 王铁和.逐步回归分析方法在农机化系统分析中的应用[J].农业机械学报,1997(1):98-101.

[15] Yen G G, Lu H. Hierarchical genetic algorithm based neural network design[C]//IEEE Xplore, 2000:168-175.

[16] Rezaeian J, Javadian N, Tavakkoli-Moghaddam R, et al. A hybrid approach based on the genetic algorithm and neural network to design an incremental cellular manufacturing system[J].Applied Soft Computing, 2011, 11(6):4195-4202.

[17] 中华人民共和国国家统计局.中国统计年鉴2015 [M].北京:中国统计出版社，2015.

[18] Herrera F, Lozano M, Verdegay J L.Tackling Real-Coded Genetic Algorithms: Operators and Tools for Behavioural Analysis[J].Artificial Intelligence Review, 1998, 12(4):265-319.

[19] Tang P H, Tseng M H. Adaptive directed mutation for real-coded genetic algorithms[J].Applied Soft Computing, 2013, 13(1):600-614.

[20] Abdulrahman O, Munetomo M, Akama K. An Adaptive Parameters Binary-Real Coded Genetic Algorithm for Real Parameter Optimization: Performance Analysis and Estimation of Optimal Control Parameters[J].International Journal of Computer Science Issues, 2012, 9(2):37-53.

[21] Yoon Y, Kim Y H. Geometricity of genetic operators for real-coded representation[J].Applied Mathematics & Computation, 2013, 219(23):10915-10927.

[22] Wang L, Zeng Y, Chen T.Back propagation neural network with adaptive differential evolution algorithm for time series forecasting[J].Expert Systems with Applications, 2015, 42(2):855-863.

[23] Gaxiola F, Melin P, Valdez F, et al.Generalized type-2 fuzzy weight adjustment for backpropagation neural networks in time series prediction[J].Information Sciences, 2015, 325(C):159-174.

[24] Faller W E, Schreck S J, Luttges M W. Neural network prediction and control of three-dimensional unsteady separated flowfields[J].Nihon Hinyōkika Gakkai Zasshi the Japanese Journal of Urology, 2015, 32(6):649-659.

[25] 刘玉静，李成华，杨升明辽宁省农机总动力组合预测与分析[J].农机化研究，2007(5)：31-33．

[26] 周振,马庆超,孔祥智.农业机械化对农村劳动力转移贡献的量化研究[J].农业技术经济,2016(2):52-62.

[27] 杨敏丽,白人朴.中国农业机械化财政投入分析[J].农业机械学报,2004(5):94-97.

[28] 李红.农机购置补贴政策效应实证分析[J].经济纵横,2008(10):67-69.

[29] 王雨濛,岳振飞,吕丹,等.农机补贴政策实施的现状问题与完善措施—来自湖北的调查[J].湖北社会科学,2015(6):69-75.

[30] 周振,张琛,彭超,等.农业机械化与农民收入:来自农机具购置补贴政策的证据[J].中国农村经济,2016(2):68-82.

[31] 杨印生,刘子玉.农业机械消费与农村居民收入的关系研究[J].统计与决策,2008(6):93-94.