X75海底管线管应变极限的数值模拟

（湖北理工学院 机电学院，湖北 黄石435003）

0 前言

随着对能源需求的日益增加，加大了对海洋石油、天然气的开发，使得海底管线在世界范围内得到广泛应用，管线建设已扩展到极地冻土带、地震区和海洋等区域，这些区域的管线可能会发生较大的塑性变形。传统的海底管道设计是基于应力的设计，即用单一的安全系数将钢管应力限制在一定的屈服强度或抗拉强度范围内[1-4]。这些安全系数实际上都是基于经验的，使得压力虽然安全但偏于保守，不能真实反映钢管性能的客观变化规律，容易造成材料浪费。而在管线钢的各项性能指标中，拉伸性能是最重要、最基本的性能，也是管道设计和安全评价最重要的依据。国外对大变形钢管进行过全尺寸实物试验，得出关于拉伸的应变极限研究成果。但目前我国不具备大口径钢管全尺寸拉伸的试验条件，因此采用数值模拟方式计算应变极限。本研究采用ANSYS软件对X75海底管线管在不同的变形条件及规格等情况下进行拉伸变形的计算模拟，分析在拉伸变形条件下应变速率、内部压强、屈强比及刚度对X75海底管线管应力应变极限的影响规律[5]，从而为分析钢管能否承受住深海环境的变形要求及管道的设计和选材提供依据。

1 X75海底管线管的拉伸极限有限元模型的建立

对于薄壁结构，如果选用实体单元，薄壁结构厚度方向的单元层数太少，计算结果误差较大，没有shell单元计算准确，但是DEFORM有限元软件中没有shell单元。ANSYS可以提供更丰富的单元用于不同结构计算，因此采用ANSYS对大变形钢管进行拉伸极限模拟计算。本研究采用shell-181单元建立了3D有限元模型[6-8]，对φ1 016 mm×21.8 m、φ1 016 mm×18.3 mm、φ813 mm×15.2 mm 三个规格钢管在拉伸变形条件下的变形极限进行模拟，分析变形速率和管内压强对钢管变形极限的影响。模拟计算参数见表1，建立的有限元模型和海底管线管的应力-应变曲线如图1、图2所示。

图1 拉伸模拟模型

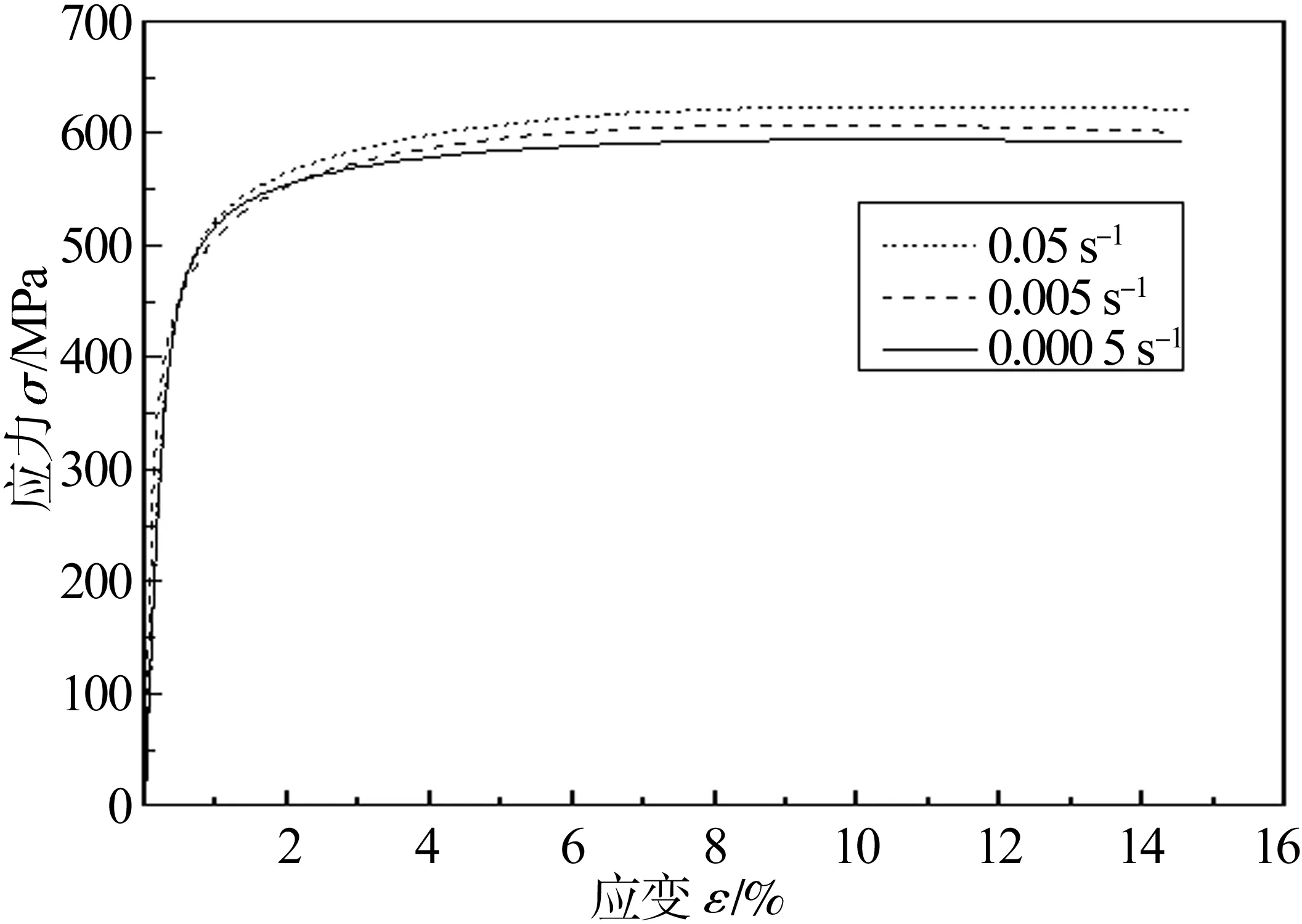
图2 应力应变曲线

表1 模拟计算参数

2 拉伸应变模拟结果分析

2.1 φ1 016×21.8钢管拉伸极限模拟结果

φ1 016×21.8钢管在不同应变速率0.000 5 s-1、0.005 s-1、0.05 s-1和内压 0 MPa、8.6 MPa、10.2 MPa、12.5 MPa、14.0 MPa下的应力-应变曲线如图3所示，不同变形速率、不同内压下的拉伸极限应力和应变见表2。

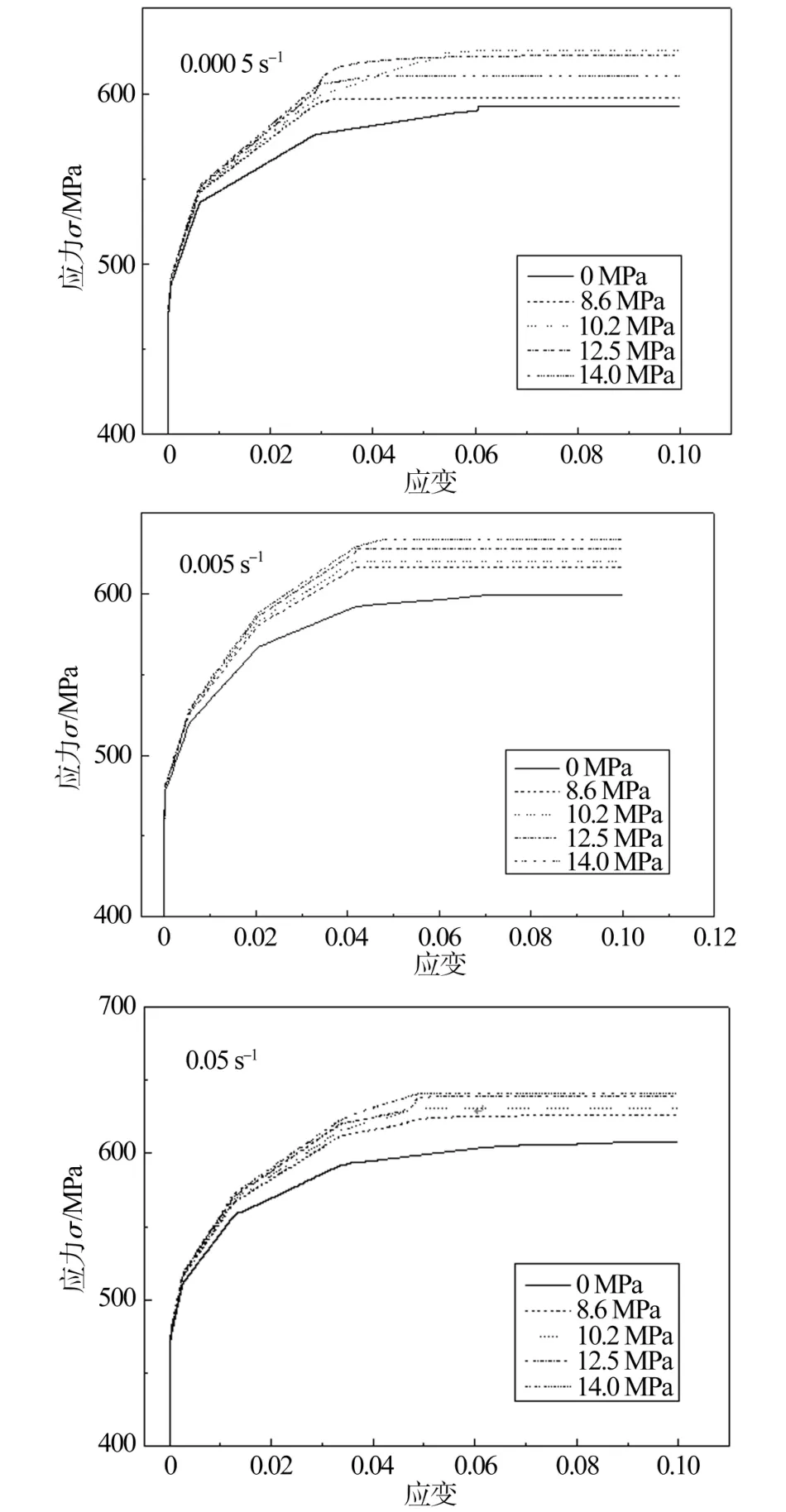
图3 φ1 016×21.8钢管不同应变速率、不同内压下的应力应变曲线

表2 φ1 016×21.8钢管不同应变速率、不同内压下的极限应力和极限应变

φ1 016×21.8钢管极限应力、极限应变的变化规律曲线如图4所示。由图3、表2和图4可以得知，当应变速率一定时，随着钢管内部压强的增大，在0.000 5 s-1的应变速率下，极限应力先增大后减小，极限应变逐渐减小；在0.005 s-1、0.05 s-1应变速率下，极限应力逐渐增大，极限应变先减小后增大[9]；当内部压强一定时，随着应变速率的增大，极限应力和极限应变在10.2 MPa内压下均呈先减小后增大的趋势，而在其他内压下均呈逐渐增大的趋势[10-11]。其原因是缺陷的存在使得原始可动位错密度随变形率变化有所波动，随着变形的进行缺陷消除，位错密度达到最大值时变形速率也达到最大值。

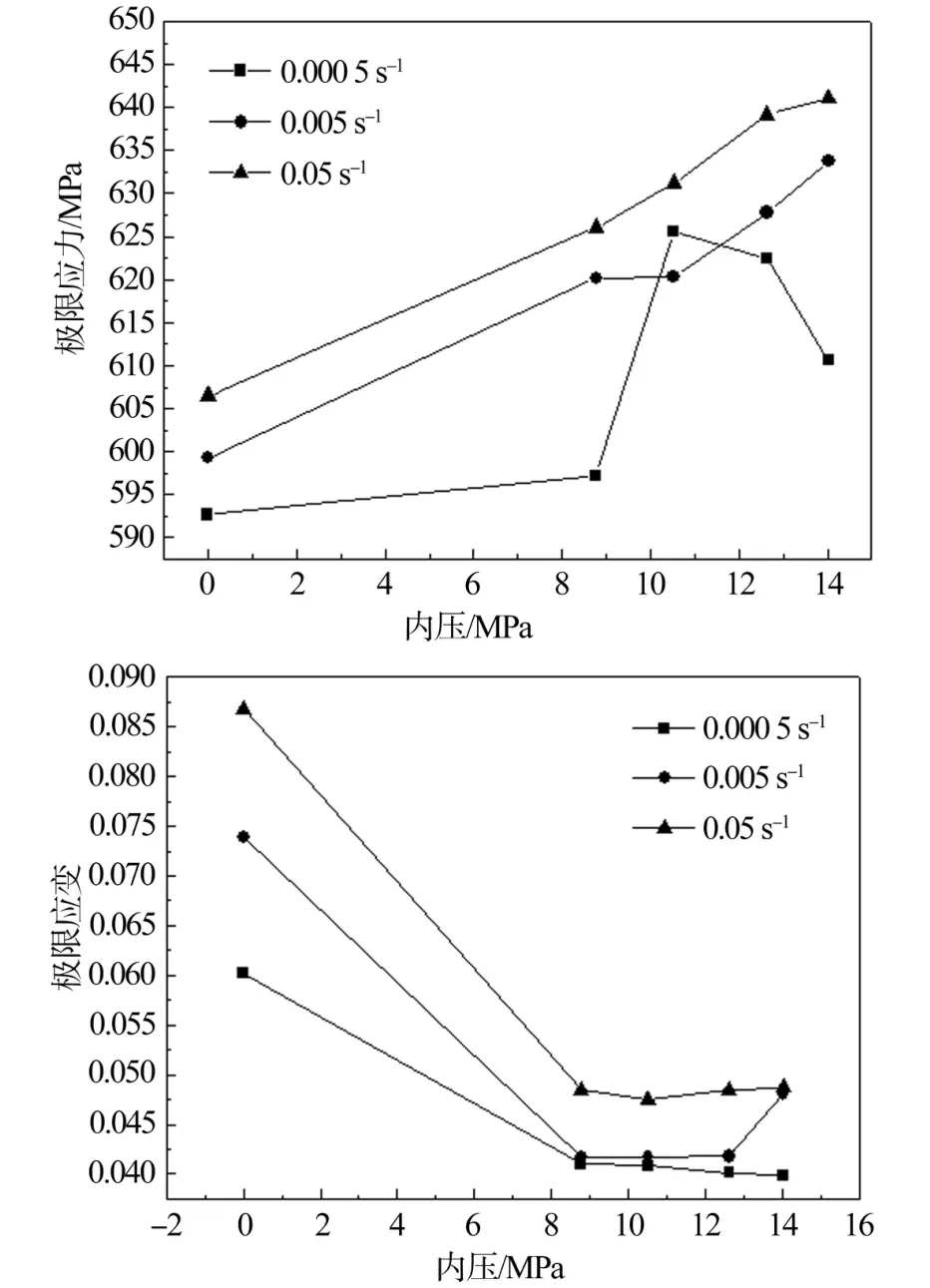
图4 φ1 016×21.8钢管极限应力、极限应变的变化规律曲线

2.2 φ1 016×21.8规格钢管屈强比对抗拉极限应力应变的影响

钢管拉伸应变速率为 0.05s-1、0.005s-1、0.0005s-1时，屈强比分别为0.77、0.79和0.78。在钢管内施加不同压强时，屈强比对抗拉极限应力应变的影响如图5、图6所示。

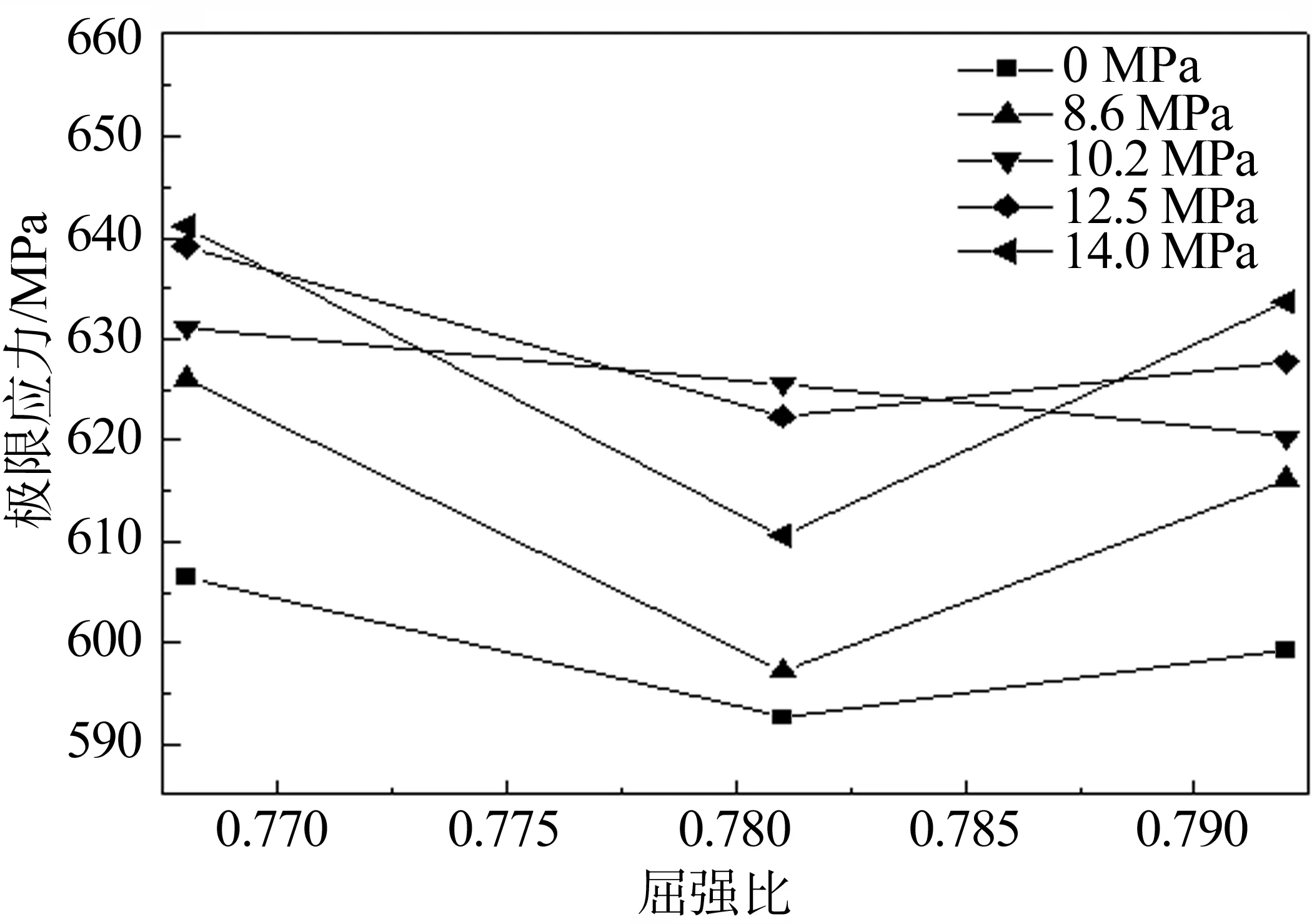
图5 屈强比对抗拉极限应力的影响

图6 屈强比对抗拉极限应变的影响

由图5、图6可知，随着屈强比的增大，抗拉极限应力在10.2 MPa内压下逐渐减小，在其他内压下呈先减小后增大；抗拉极限应变在10.2 MPa内压下先增大后减小，其他内压下先减小后增大。可见，屈强比对极限应力、极限应变的影响趋势一致，应力是引起应变的原因，管线钢在实验受力条件下，应力与应变的变化趋势一致，极限应力达到最大值，加工硬化现象达到最大程度，极限应变随即达到最大值。

2.3 刚度（D/t）对抗拉极限应力应变的影响

φ1 016×21.8、φ1 016×18.3 和 φ813×15.2 三种规格海底管线管对应的刚度分别为46.606、55.519和53.487，选择0.005 s-1应变速率，钢管内部分别施加 0 MPa、8.6 MPa、10.2 MPa、12.5 MPa、14.0 MPa 五种不同的标准压强，刚度对抗拉应力应变极限的影响规律如图7、图8所示；选择8.6 MPa内部压强，采用 0.000 5 s-1、0.005 s-1、0.05 s-1三种不同的应变速率进行整管拉伸，刚度对抗拉应力应变极限的影响规律如图9、图10所示。

图7 不同内压下刚度对抗拉极限应力的影响

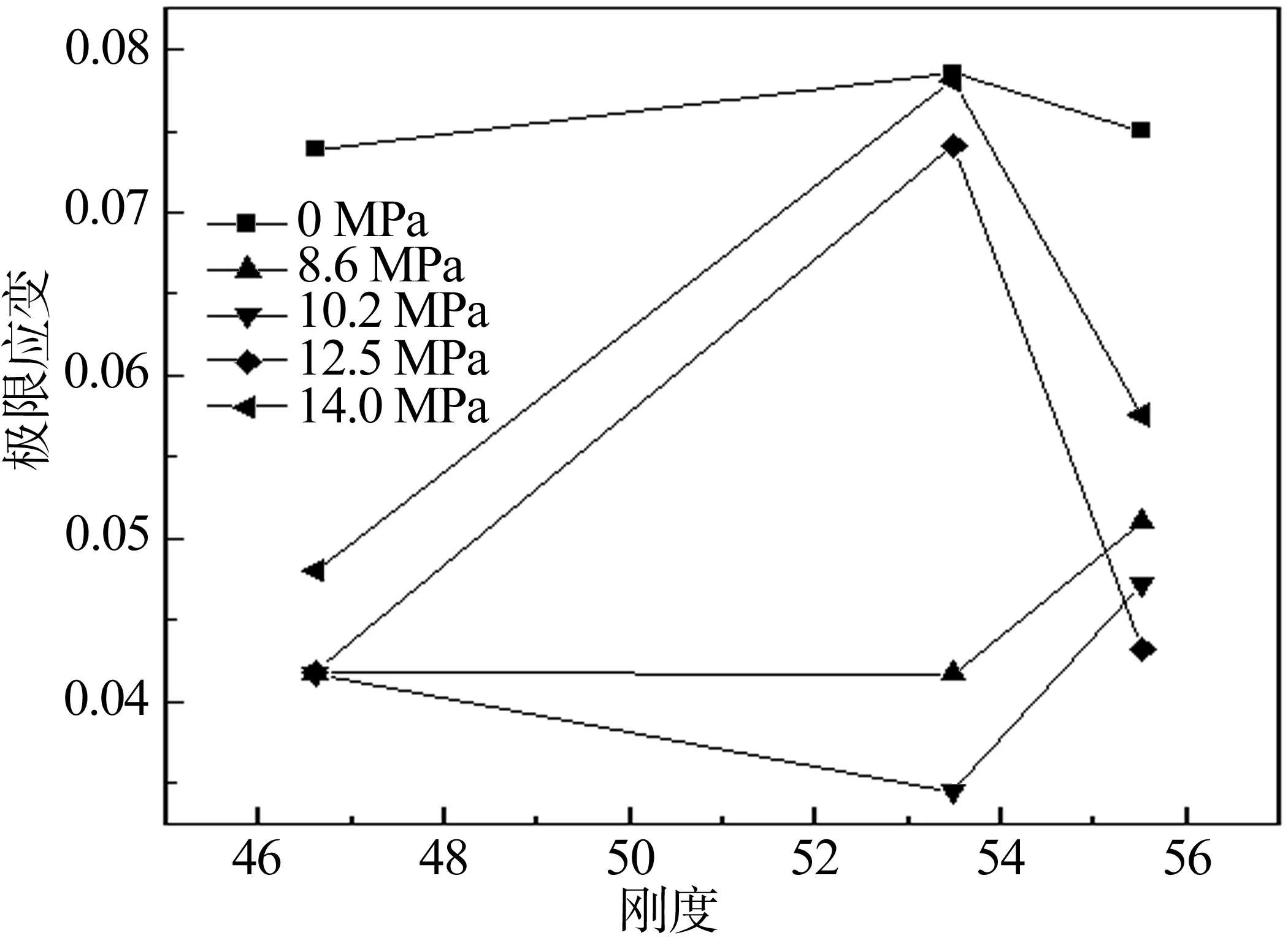
图8 不同内压下刚度对抗拉极限应变的影响

图9 不同应变速率下刚度对抗拉极限应力的影响

由图7、图8可知，随着刚度的增大，抗拉极限应力和抗拉极限应变在0 MPa内压下变化不大，在12.5 MPa、14.0 MPa内压下先增大后减小，其他内压下先减小后增大。

图10 不同应变速率下刚度对抗拉极限应变的影响

由图9、图10可知，随着刚度的增加，抗拉极限应力在0.000 5 s-1的应变速率下先增大后减小，在0.005 s-1、0.05 s-1的应变速率下逐渐增大；抗拉极限应变在0.000 5 s-1的应变速率下先减小后增大，在0.005 s-1、0.05 s-1的应变速率下先增大后减小。可见，刚度对应力与应变的影响较为复杂，用两者的综合参量即应变能来分析更为直观，刚度越大，变形能梯度趋于平缓，抗拉极限应力增大，使得应变极限总体呈减小趋势。

3 结论

（1）当应变速率一定时，随着管内压强的增大，在0.0005s-1应变速率下，极限应力先增大后减小，极限应变逐渐减小；在0.005 s-1、0.05 s-1应变速率下，极限应力逐渐增大，极限应变先减小后增大。

（2）当内部压强一定时，随着应变速率的增大，极限应力和极限应变整体上呈逐渐增大趋势。

（3）随着屈强比的增大，抗拉极限应力和抗拉极限应变整体上呈先减小后增大趋势。

（4）当应变速率一定时，随着刚度的增大，抗拉极限应力及抗拉极限应变在0 MPa内压下变化不大，12.5 MPa、14.0 MPa内压下先增大后减小，其他内压下呈先减小后增大趋势。当内压一定时，随着刚度的增加，在0.000 5 s-1应变速率下，抗拉极限应力先增大后减小，抗拉极限应变先减小后增大；在0.005 s-1、0.05 s-1应变速率下，抗拉极限应变逐渐增大，抗拉极限应变先增大后减小。

[1]郑磊，傅俊岩.高等级管线钢的发展现状[J].钢铁，2006，41（10）：1-10.

[2]李鹤林，李霄，吉玲康，等.油气管道基于应变的设计及抗大变形管线钢的开发与应用[J].焊管，2007，30（5）：19-25.

[3]樊学华，李向阳，董磊，等.国内抗大变形管线钢研究及应用进展[J].油气储运，2015（3）：237-243.

[4]张振宇，冯垚，杨继忠，等.我国大变形输送管技术现状[J].化工管理，2015（3）：144-144.

[5]王名洋，刘冰，张宏.管道拉伸应变极限确定方法[J].管道技术与设备，2011（2）：4-6.

[6]张蓉.304不锈钢拉深成形的物理模拟与数值模拟研究[D].湖南：中南大学，2007：47-75.

[7]倪栋.通用有限元分析ANSYS 7.0实例精解[M].北京：电子工业出版社，2003.

[8]García-Garino C，Gabaldón F，Goicolea J M.Finite element simulation of the simple tension test in metals[J].Finite Elements in Analysis&Design，2006，42（13）：1187-1197.

[9]郑茂盛，周根树，赵新伟，等.现役油气管道安全性评价研究现状[J].石油工程建设，2004，30（1）：1-6.

[10]孙宏.拉伸试验速率对X80级管线钢拉伸试验结果的影响[J].焊管，2009，32（1）：53-55.

[11]Baek J H，Kim Y P，Kim C M，et al.Effects of pre-strain on the mechanical properties of API 5L X65 pipe[J].Materials Science&Engineering A，2010，527（6）：1473-1479.