先进出行信息下事故对行程时间可靠性的影响

刘永红，李进龙，陈 欣，罗 霞

(西南交通大学交通运输与物流学院，成都611756)

0 引言

路网可靠性是在指定服务水平、规定条件下完成预定功能的能力.导致路网不可靠的随机因素有很多，比如日常的道路拥挤和日变的交通需求称为可重复性因素，自然灾害、偶发的交通事故等称为不可重复性因素.路网可靠性的研究主要集中在3个方面：路网连通度的研究、行程时间可靠性的研究、容量可靠性的研究.在上述路网可靠性评价指标体系中，行程时间可靠性是一个衡量路网可靠性非常重要的指标，Askura[1]和Bell[2]等将行程时间可靠性定义为给定的OD对能够在给定的服务水平下在一定时间内到达目的地的概率，它与道路交通网络的状态直接相关，是一个更能为出行者所接受的效用测度.

近年来，国内外针对路网的行程时间可靠性做了大量研究.Chen等[3-4]定义了行程时间可靠性为交通出行能够在某一时间范围内完成的概率，对风险敏感型出行者的出行时间可靠性进行了研究；Du等[5]在交通供给变动的情况下，讨论了路段通行能力下降对路网可靠度的影响；Stephen等[6]考虑了日常交通需求的随机变动，利用统计方法确定总行程时间概率密度函数族，实现了路网可靠度的估计.陈玲娟等[7]通过路段传输模型，提出了交通事故发生后基于Monte-Carlo法的路网行程时间算法；冷军强等[8]从路段角度层面定义行程时间可靠性，研究出行者对待风险的态度对行程时间可靠性的影响；Xu等[9]研究了需求弹性变化时出行者的出行行为，从而对可靠度进行估计.先进的出行者信息系统(ATIS)是智能运输系统(ITS)的重要组成部分，相关研究引起了越来越多研究者的兴趣.文献[10]研究了在出行信息为出行者提供实时的路况信息时，驾驶员根据这些信息调整其路径的决策行为；文献[11]研究了有ATIS下出行者基于平均出行时间和无ATIS下出行者基于有效时间进行混合均衡分配问题；文献[12]在交通网络实现用户均衡态的过程中，引入决策出行费用的概念，提出了在ATIS环境下的交通配流动态演化模型；文献[13]基于元胞传输模型，提出新的出行时间计算方法，针对重复性拥堵和非重复性拥堵，分析交通信息对交通流的影响；文献[14]将出行者划分为有ATIS和无ATIS接受装置，以随机方式选择路网，构建了随机用户均衡模型，以此来讨论信息环境对出行时间可靠度的影响；文献[15]利用随机过程的数字特征确定路段行驶时间，以Logit模型为基础考虑出行对出行线路信息储备的异质性，建立了出行时间可靠性的完整模型.上述文献虽然给出了行程时间可靠性的定义和方法，但是大都是基于静态路网计算路段出行时间或者考虑了信息质量单一方面对路网可靠性的影响，将重复性因素中的通行能力、交通需求作为随机变量研究路网中的可靠性，对信息环境下突发交通事故的路网可靠性研究较少.

本文考虑非重复性因素，交通事故对行程时间可靠性的影响.以事故持续时间作为随机变量，从路径行程时间可靠性出发，考虑在ATIS环境下，利用元胞传输模型对路网流量进行拟动态加载，研究了事故持续时间对路网行程时间可靠性的影响，并分析了在事故持续时间一定时，交通需求的变化及事故严重程度对行程时间可靠性的影响.

1 路网行程时间可靠性

假定事故持续时间T，T∼N(μ,σ)，事故持续时间的随机性导致路径走行时间的随机性；考虑交通网路G=(N ,A)，其中N为节点集，A为路段集；用W表示起讫点OD的集合，R表示起点集合，S表示讫点集合，m表示OD对rs的路径集合；将时域[0 , T]划分为K个相等的时段Δt=T K，时段编号k=1,2,3,…,K.通过元胞传输模型拟动态加载路网流量，可获得k时段出发OD对rs间选择路径p的出行流量fprs(k)的出行时间，从而该路径在T内的平均走行时间Tprs为

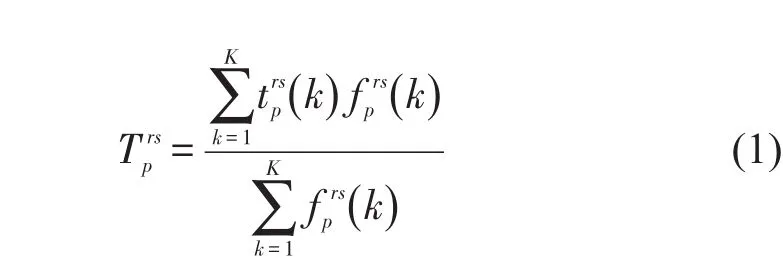
式中：fprs(k)为第k时段OD对rs间沿路径p出发的流量；trps(k)为fprs(k)达到终点的出行时间.通过元胞传输模型可以得到每一个时段内各路段上流出和流入的流量，进而求出各个时段内路径的行程时间，在ATIS环境下，通过信息的实时传输，出行者在出发点k时段开始可以知道上一时段k-1结束时各条路径的出行时间，出行者进行决策时以此为依据进行路径决策.假设：不考虑信息传播的延时性，在ATIS环境下出行信息可以在每一个时段结束时实时更新，包括事故发生时间、持续时间、上一时段各条路径的出行时间，并且所有出行者在起始点均已知该时段的路径走行时间.

出行者对路径走行时间的理解存在随机误差，假设该误差服从Gumbel分布，可以用Logit来对出行者路径选择行为进行描述，路径选择概率为

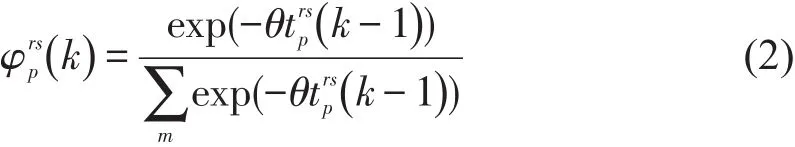
式中：φrps(k)为时段k开始出发在OD 对rs之间选择路径p的概率.

1.1 元胞传输模型动态加载流量

元胞传输模型(CTM)将路段划分为长度相等的多个元胞，且研究时域离散成相等的时段后，使得元胞的长度等于单个时段内自由流走行的距离，车辆在路段上的位置变化为车辆从一个元胞进入另一个元胞.Daganzo[16]提出，如果交通量q和交通密度ρ满足

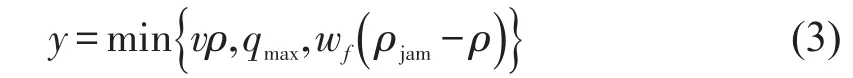
则连续交通流有式(4)和式(5)的关系.

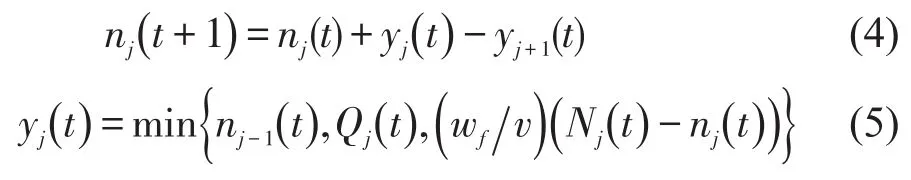
式中：v 、qmax、wf、ρjam分别是元胞内自由流速度、最大交通量、激波的速度和堵塞密度；nj(t)、yj(t)、Nj(t)、Qj(t)分别代表t时刻元胞j内的车辆数、车辆实际流入率、1个元胞最多能够承载的车辆数、元胞所能接受的最大流入率；下标j+1、j-1分别代表元胞j的下游和上游元胞

路网节点处交通流的演化一般有以下3种输入输出类型：①简单连接的相邻元胞，②处于合流点的元胞，③处于分流点的元胞.令(Nj(t)-nj(t) ) }分别表示t时刻元胞j-1能够驶入下游元胞j的流量和t时刻元胞j能够容纳的上游元胞流量；βj-1(t)、βj-2(t) 分别表示t时刻从元胞 j-1、j-2流入元胞j的流量比例；βj+1(t)、βj+2(t) 分别表示t时刻从元胞j流入元胞j+1、j+2的流量比例.

普通元胞演变关系为

合流元胞演变关系为

当 Rj(t)≥Sj-1(t)+Sj-2(t) 时，

当Rj(t)＜Sj-1(t)+Sj-2(t) 时，

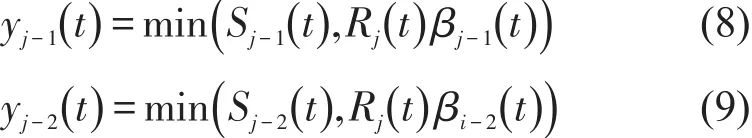
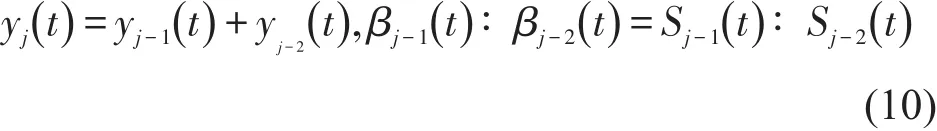
分流元胞演变关系为

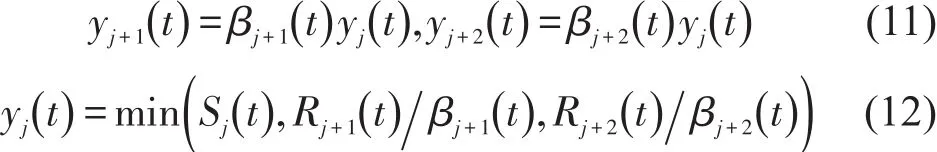
1.2 路径出行时间

令分别表示到时段t为止选择路径p离开起始元胞O的流量和时段k为止选择路径p达到终点元胞D的流量；表示时段选择路径p达到元胞D的流量[17]，则：

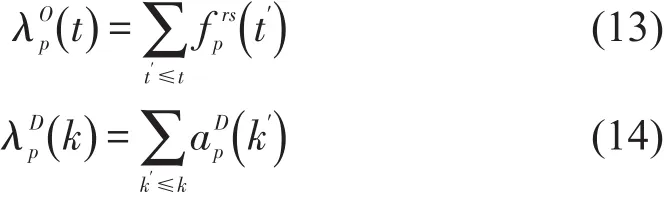
k时段选择路径p出发的流量fprs(k)在k+m时段为止全部达到终点元胞，即，ft代表fprs(k)中第k+t时段达到终点元胞的流量.考虑到车流从起点到终点需要一定时间的步长，将时域划分后，采用元胞传输拟动态加载车流方法，计算ft的时候采用迭代思想.从第1时段出发的车流开始计算.

如果，则

如果，则

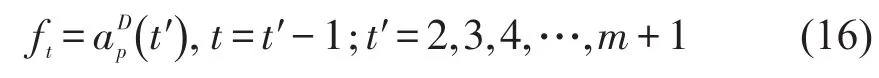
第k时段出发流量的ft可以通过式(17)和式(18)计算

如 果，则

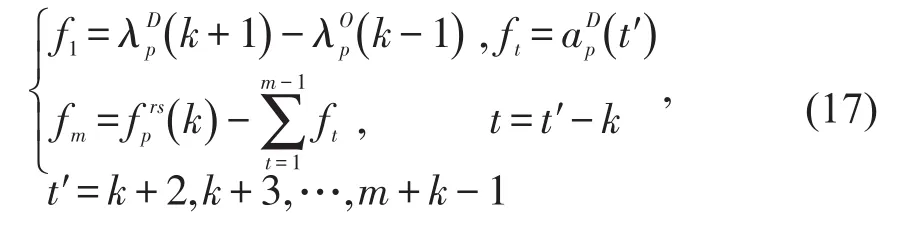
如果，则

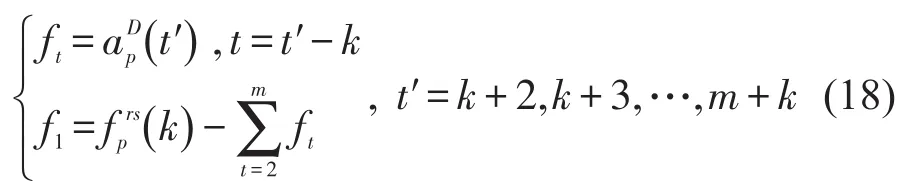
其他时段以此类推.因此流量fprs(k)的出行时间可以通过平均出行时间进行计算.

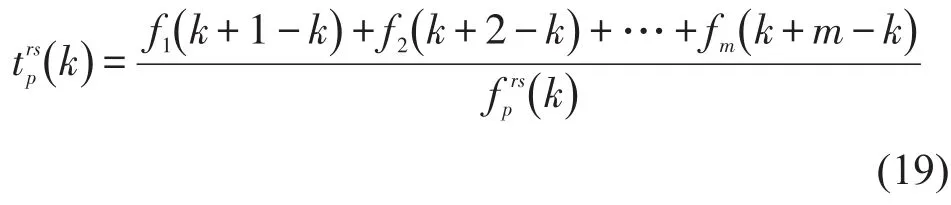
1.3 行程时间可靠性

假定交通事故的持续时间服从给定的分布，根据元胞传输模型，在路网中拟动态加载流量.根据流量得到每一时段各条路径的出行时间，出行者在下一时刻根据ATIS提供的路径出行时间进行路径决策，最后可以得到各个时段的路径出行时间和网络加载流量，据此计算整个路网的出行时间可靠性.本文采用基于Monte-Carlo的模拟方法近似计算可靠性步骤如下：

(1)初始化，用Monte-Carrlo方法抽取1组满足事故持续时间概率分布的Nmax个数值.

(2)将产生的第i个随机数带入路网，根据路径选择原则和元胞传输模型，求解出该随机数下路网的各路径走行时间Tprs(i)，定义该随机数下事故持续时间内路径出行时间的可靠性Rrps(i)为

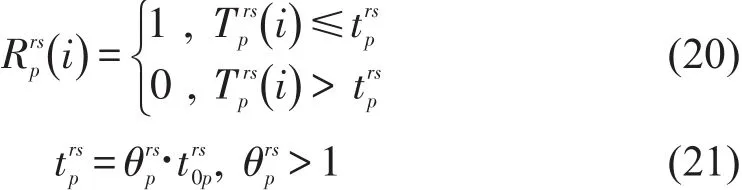
式中：tr0s p为事故发生前路径的平均走行时间；θrps为事故发生后的拥堵系数，反映出行者可接受的拥堵水平.

(3)将所有随机数全部带入路网进行求解之后，令

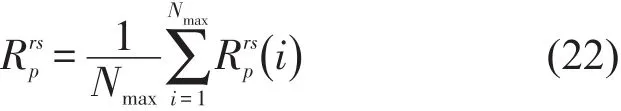
(4)通常在路网中同一OD 对之间有多条路径，按照并联系统可靠性分析理论对OD 对rs之间的出行时间可靠性Rrs计算.

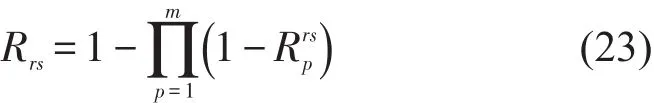
实际的路网通常具有多个起讫点，在求得每一OD出行时间可靠性的基础上，经过线性加权的方式求得整个路网出行时间可靠性R为

式中：qrs为OD 对rs之间的流量.

2 实例分析

算例路网如图1所示.假设路段a1的通行能力为1.5 veh/s，a2、a3的通行能力为1.0 veh/s，路段a4、a7的通行能力为0.3 veh/s，路段a5、a6的通行能力为0.4 veh/s，假定路段上的流量—密度关系式满足式(3)，堵塞密度ρjam为125 veh/km，自由流速度为25 m/s，交通激波向后的传播的速度wf为15 m/s.

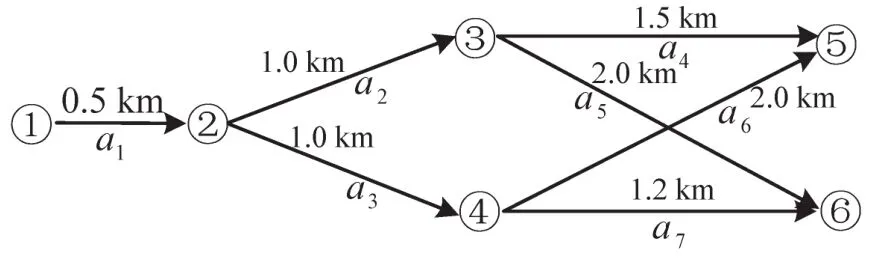
图1 算例网路图Fig.1 Numerical network diagram

离散化后每个时段间隔Δt=5 s，假设节点①的输出能力无限大，即N1(t)=∞；节点⑤和节点⑥具有无限大的承载能力，即Q5(t)=∞，Q6(t)=∞.在第501 s时，路段a4在距离节点③750 m处发生交通事故，路段的通行能力下降值α=3 4，事故的持续时间服从均值为μ，方差为σ的正态分布.Logit设定的参数θ=0.1，θrps取值分别为2.8，3.0，Nmax=100.DK为交通需求，DK(1),DK(2)分别表示OD对①⑤和①⑥间的交通需求.

得到不同事故持续时间均值与路网可靠性的关系如图2所示，DK(1)=DK(2)；不同事故持续时间方差与路网可靠性的关系如图3所示，DK(1)=DK(2).图2比较了不同事故持续时间均值和不同交通需求下可靠性的变化趋势，可以得出事故持续时间越长，可靠性越低；图3给出了不同事故持续时间方差和不同出行需求的可靠性对比，可以看出事故持续时间方差越大，可靠性越低.

图2 可靠性与持续时间均值的关系Fig.2 The relationship between travel time reliability and mean of incident duration

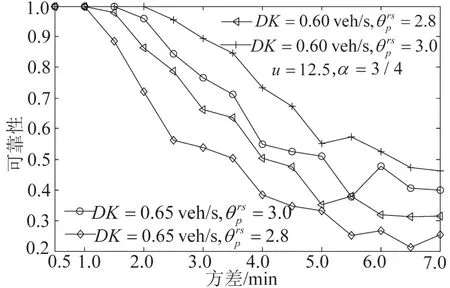
图3 事故持续时间方差与可靠性的关系Fig.3 The relationship between travel time reliability and variance of the duration

图4比较了不同交通需求和不同事故严重程度(事故越严重，发生事故后，该路段通行能力与原通行能力比值越小)下的可靠性对比，DK(1)=DK(2).可以看出在给定的可接受拥堵水平下，当事故发生后，通行能力大于等于事故前的0.65时，此时即使发生事故，路网的能力也能大致满足需求，可靠性不会发生显著变化；随着事故严重程度的加重，事故路段通行能力逐渐小于事故前的0.65，事故的发生使路网的能力愈发不能满足需求，可靠性逐渐变小.当事故严重程度导致路网从非拥堵变成拥堵时，路网可靠性发生显著变化，事故越严重，路网的可靠性越低.

得到不同出行需求与可靠性的关系如图5所示.DK(1)，DK(2)不同时，(DK(2)+DK(1))2的变化区间为[0.40,0.85]veh/s；可以得出需求越大，可靠性越低.事故发生在OD对①⑤间路段a4上，当交通需求不是很大时，路网处于非拥堵状态，此时事故发生，OD对①⑤间选择路径a1→a2→a4的部分车流会选择其他道路，导致OD对①⑥间道路流量增加，因此，此时OD对①⑥间流量越大时，路网可靠性越低；随着需求的增加，可靠性降低，需求超过路网能力的一定范围时，OD对间流量均衡时，路网可靠性最高；随着需求的持续增加，路网处于拥堵状态，此时包含事故路段的OD对需求越大，路网可靠性越低.

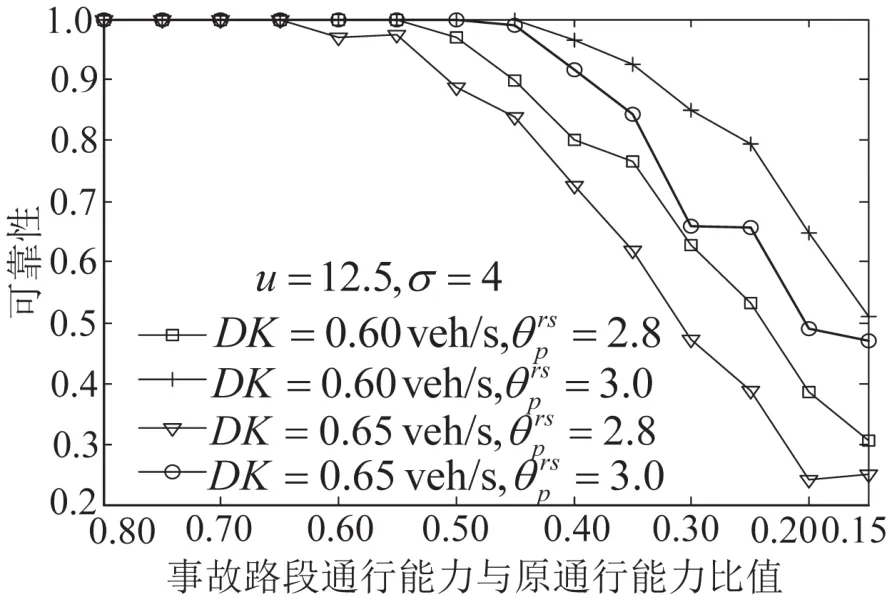
图4 可靠性与事故路段通行能力变化量的关系Fig.4 The relationship between travel time reliability and the ratio of the capacity of the incident road to original capacity

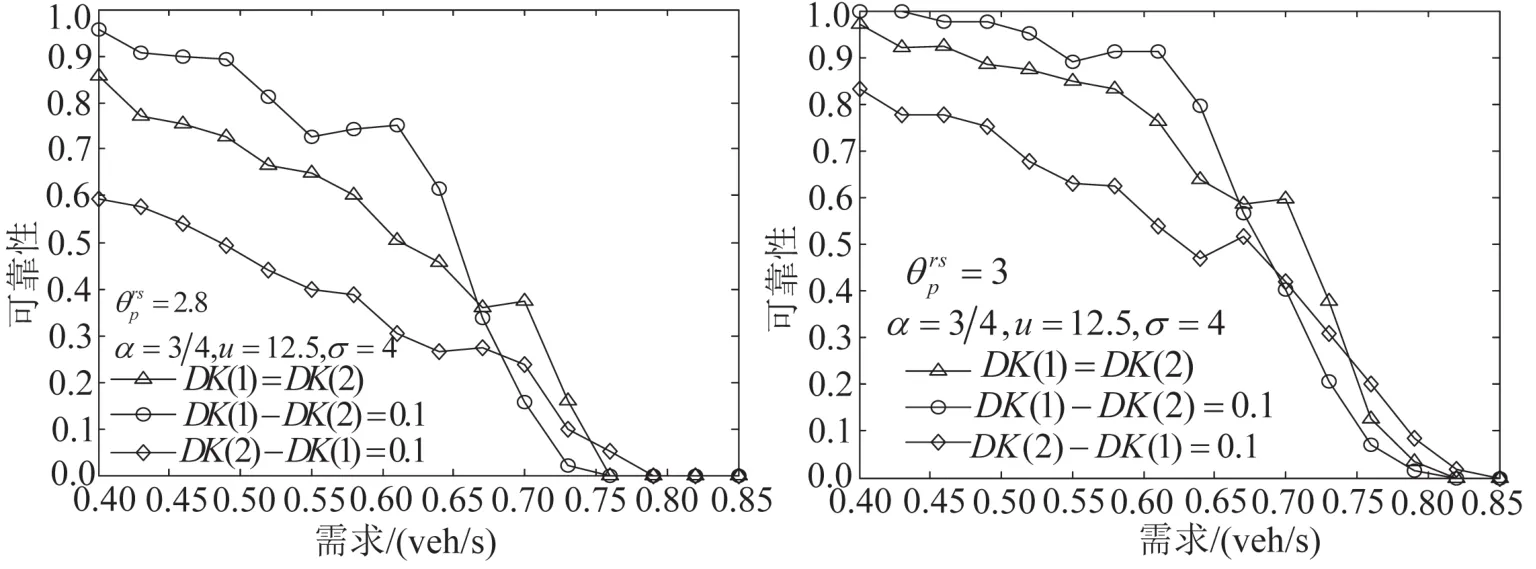
图5 交通需求的变化与可靠性的关系Fig.5 The relationship between travel time relationship and the change of travel demand

结合图2～图5可以看出，出行者可接受的拥堵水平越高，即θrps越大，可靠性越高.

3 结论

本文考虑在ATIS环境下，建立了以元胞传输模型和Logit模型为基础的拟动态模型，加载了动态网络流量，得出了各时间间隔内各个元胞的流入、流出车辆数和路径走行时间，研究了事故持续时间、方差和事故持续时间一定时，事故的严重程度，以及包含事故路段OD需求不同时对路网可靠性的影响.定义了交通事故发生后路径行程时间可靠性为在整个事故持续期间内平均路径走行时间小于一定阈值的概率，并按照并联系统求出OD间行程时间可靠性，进而根据OD对不同需求得到路网行程时间可靠性，给出了不同条件下的路网行程时间可靠性.算例结果表明：

(1)事故持续时间越长，可靠性越低；事故持续时间方差越大，路网可靠性越低.

(2)交通需求越大，可靠性越低；事故对局部通行能力影响越严重，可靠性越低；出行者可接受拥堵水平越高，可靠性越高.

(3)路网交通需求不大时，即路网处于非拥堵状态，此时包含事故路段的OD对需求越高，路网可靠性越高；随着需求不断增大，达到路网能力时，发生事故，OD对间需求越均衡时，路网可靠性越高；需求持续增大，路网处于拥堵状态，包含事故路段的OD对需求越高，路网可靠性越低.

交通事故的发生具有随机性，本文只研究了在路网某一路段发生交通事故时对路网行程时间可靠性的影响，下一步的研究方向是在ATIS环境下路网中不同路段同时发生交通事故对可靠性的影响.

[1]ASAKURA Y.Reliability measures of an origin and destination pair in a deteriorated road network with variable flows[C]//Proceeding of the Fourth Meeting of the EURO Working Group in Transportation,New York：Amsterdam,1999：273-287.

[2]BELL M,CASSIR C IIDA Y,et al.A sensitivity-based approach to network reliability assentment[J].Proceedings of the 14th International Symposium on Transportation and Traffic Theory,Jerusalem,1999：283-300.

[3]CHEN A,YANG H,LO HK,et al.A capacity related reliability fortransportation network[J].Journalof Advanced Transportation Network,1999,33(2)：183-200.

[4]CHEN A,JI Z,RECKER W.Travel time reliability with risk-sensitive travelers[J]. Transportation Research Record Journal of the Transportation Research Board,2001,1783(1)：27-33.

[5]DU Z P,NICHOSLON A J.Degradable transportation systems：Sensitivity and reliability analysis[J].Transportation Research Part B,1997,31(3)：225-237.

[6]STEPHEN C,DAVID W.Modeling network travel time reliability under stochastic demand[J].Transportation Research Part B,2005,39(3)：119-140.

[7]陈玲娟，刘海旭，蒲云.交通事故持续期内行程时间的可靠性研究[J].西南交通大学学报,2013,48(2)：377-382.[CHEN L J,Liu H X,PU Y.Travel time reliability during incident duration time[J].Journal of Southwest Jiaotong University,2013,48(2)：377-382.]

[8]冷军强,张亚军,赵兴奎,等.基于广义出行费用的城市路网行程时间可靠性[J].公路交通科技,2010,27(7)：133-137.[LENG J Q,ZHANG Y J,ZHAO X K,et al.Time reliability of urban road network based on generalized travel cost[J].Journal of Highway and Transportation Research and Development,2010,27(7)：133-137.]

[9]XU M,GAO Z Y.Behaviors in a dynamic model of traffic assignmentwith elasticdemand[J].Chinese Physic,2007,16(6)：1608-1614.

[10]FIRESZ T L,BERSEIN D H,MEHTA N J,et al.Dayto-day dynamic network disequilibrium and idealized traveler information systems[J].Operation Research,1994,42(6)：1120-1136.

[11]SHAO H,TIAN Q,YUANG X M,et al.Risk-taking path choice behaviors under ATIS in transportation networks with demand uncertainty[J].Journal of Southeast University,2008,24(sup)：43-48.

[12]郭仁拥,黄海军.ATIS环境下交通配流的动态演化模型[J].管理科学学报,2008,11(2)：12-19.[GUO R Y,HUANG H J.The dynamic evolution model of traffic distribution in the ATIS environment[J].Journal of Management Sciences in China,2008,11(2)：12-19.]

[13]尚华艳,黄海军,高自友.基于元胞传输模型的实时交通信息设计[J].北京航空航天大学学报,2008,34(2)：234-238.[SHANG H Y,HUANG H J,GAO Z Y,et al.Design real-time traffic information by cell transmission model[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(2)：234-238.]

[14]黄忠祥,况爱武,范文婷,等.出行信息对道路网络出行时间可靠性的影响[J].交通运输系统工程与信息,2012,12(6)：93-99.[HUANG Z X,KUANG A W,FAN W T,et al.Impact of travel information on road network traveltime reliability[J].JournalofTransportation Systems Engineering and Information Technology,2012,12(6)：93-99.]

[15]侯立文,谭家美.信息条件下路段出行时间可靠性的计算[J].上海交通大学学报,2006,40(6)：968-972.[HOU L W,TAN J M.Computing the link travel time reliabilitywith information provision[J].Journalof Shanghai Jiaotong University,2006,40(6)：968-972.]

[16]HONG K,LO W,SZETO Y.A cell-based variational inequality formulation of the dynamic user optimal assignment Problem[J]. Journal of Transportation Research Part B,2006,36(5)：421-443.

[17]CARLOS F,DAGANZO.The cell transmission model PartⅡ：Network traffic[J].Transportation Research Part B,1995,29(2)：79-93.