无设备定位的射频层析成像求逆算法研究

钱 慧，刘焕林

（福州大学 物理与信息工程学院，福建 福州 350116）

0 引 言

随着物联网技术的不断进步，未来传感器节点的数量将呈现爆炸式增长，这种趋势下，物联网为人类提供的业务种类会越来越多[1-3]。无线传感网络（Wireless Sensor Network，WSN）是物联网的重要组成部分，利用其实现对网络区域内目标的定位已成为研究热点之一。射频层析成像（Radio Tomographic Imaging， RTI）以无线通信传输的衰减模型为基础，是一种新兴的用于对WSN中物体造成的衰减进行成像的技术。自2009年美国犹他大学学者Joey Wilson和Neal Patwari提出该技术以来，本领域的研究重心主要集中在室内外定位、目标追踪和模式识别方面[4-6]。为提升系统性能，研究人员针对重构算法、物理模型进行了深入的研究[7-10]。目前该技术主要应用于室内定位，在不同的应用场景下如何选取重构算法对RTI系统的推广至关重要[11]。

一般情况下，时间开销和空间开销是评价算法好坏的主要评价指标。时间开销越小，算法的计算速度越快，越有利于实现数据的实时处理；空间开销越小，算法对计算机内存的占用率越小，不会过多地影响其并行处理。结合RTI系统的自身情况，实现数据地的实时处理有利于对目标的准确追踪，因此时间开销是首要考虑的因素。相比之下，由于算法的输入数据量不是很大，因此空间开销并非十分重要。除此之外，RTI重构算法还需兼顾算法的性能和重构信号质量。与常规室内定位不同的是，RTI系统输出的是二维图像信号，具有可视化功能，噪声的形式和大小对人的主观判断至关重要。就RTI系统而言，可采用定位稳定性和定位误差评价系统性能。

本文采用ZigBee节点搭建无线传感网络，采集实地接收信号强度值（Received Signal Strength，RSS）。利用计算机仿真的优势，对典型的三种重构算法（Tikhonov正则化、k-SVD和TV正则化）从计算时间、图像质量、系统性能和重构图像尺寸四个方面进行了系统性分析，在分析图像质量部分引入了全参考图质量评价方法。

1 系统设计

RTI系统网络部署如图1所示。考虑该WSN中的某条通信链路i，链路上接收节点的RSS值yi（t）有五种主要因素的影响：发送节点的功率（Pi）；由收发节点之间的距离、天线模式等造成的静态损耗（Li）；物体阻挡造成的阴影损耗（Si（t））；多径效应的影响（Fi（t））；RSS测量噪声与模型不理想造成的影响（vi（t））。

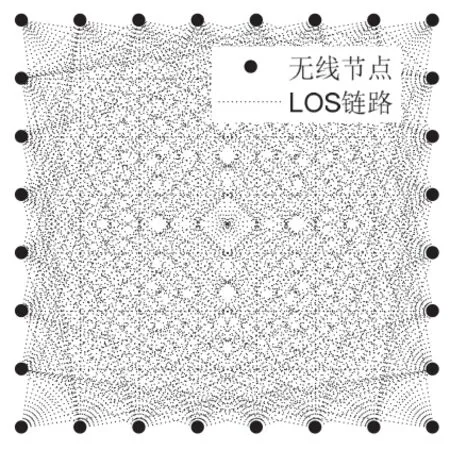
图1 RTI系统网络布置示意图

其中，Pi和Li可近似地认为不随时间变化；为了简化问题，本文只考虑视距链路（Line of Sight， LoS）上的衰减，所以Fi（t）和vi（t）可被看成是RTI系统的噪声项。接收节点的RSS值可被描述成如下形式：

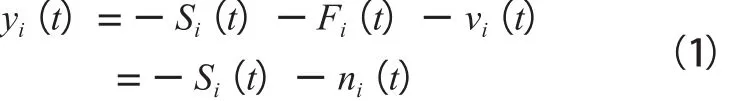
进一步考虑阴影损耗Si（t）：

其中：xj（t）表示在t时刻发生在像素j上的衰减；wij表示像素j上发生的衰减对链路i上RSS值大小的影响。一般情况下，RTI系统工作时，WSN工作在两种状态，即空状态和工作状态。空状态是WSN区域在系统工作前所处的一种状态。基于衰减模型的RTI系统的工作原理是：利用区域内工作状态和空状态下电磁场的变化实现对人们行为的感知：

至此仅考虑了WSN中的一条通信链路，为了说明整个系统，下文将采用矩阵的形式：

其中，

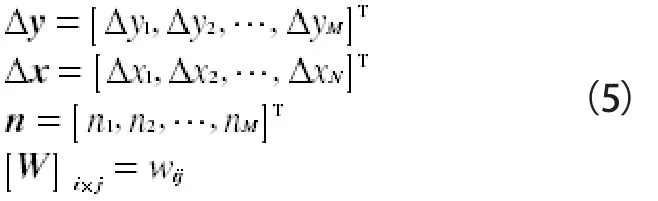
式（4）中W的维数为M×N，M代表无向链路的条数，N为重构图的像素个数，i代表链路标号，j为像素的标号。W是RTI系统的关键部分，称作系统模型，本文引用文献[3]中提出的归一化椭圆模型计算。该模型认为：以收发节点为焦点的椭圆区域内存在权重，权重大小与收发节点有关，此区域外的权重均为零。该模型被定义如下：

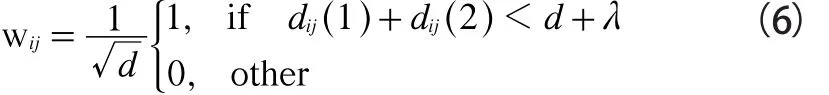
其中：d是第i条链路收发节点之间的距离，dij（1）和dij（2）分别为第j个像素的中心点到第i条链路收发节点之间的距离，λ是一个调节椭圆宽度的可控变量。

2 重构算法

许多物理线性模型都可以进行如下描述：

其中：y∈RM是测量数据，W∈RM+N是变换矩阵，n∈RM是测量噪声向量，x∈RN是待求解信号，这里M＜N。由于M＜N，式（7）存在着无穷解，即已知y和W时，无法求x的唯一解。本文将RSS的变化值表示为y，像素区域电磁场相对于空状态的变化值表示为x，这样式（4）和（7）等价。正则化方法是求解病态反问题的主要工具。

正则化的思想是：通过添加正则化项，达到约束解的范围的目的。正则化方法需要已知x的先验知识g（x）。通常利用正则化方法求解问题（7），即求解式（8）：

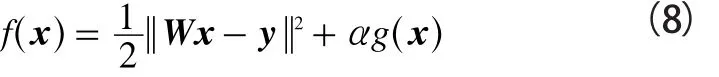
式（9）和式（10）分别为Tikhonov和TV正则化的约束项：

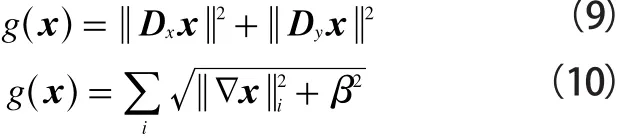
在RTI系统中，Dx和Dy分别为重构图的横向和竖向差分运算符。从式（9）和（10）中不难发现，Tikhonov正则化方法通过化简可转化成线性问题（11），TV正则化是一个非线性求解过程：

RTI成像问题是一个病态问题。在病态系统中，输入数据y的微小变化都有可能使重构信号x发生巨大变化，导致整个系统变得非常不稳定。这一点可通过对W做奇异值分解（Singular Value Decomposition，SVD）直观地看出来：

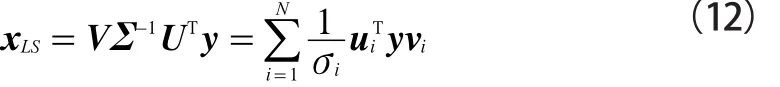
其中：U和V是酉矩阵，Σ是奇异值矩阵。k-SVD算法通过剔除模型矩阵W中较小的奇异值，保留其中前k个主要成分实现求解：

奇异值向量取决于系统本身（像是系统模型），使得该算法的求解往往与期望解偏差较大，这是因为它没有用到x的先验知识。

图2 RTI重构图与参考图

利用正则化方法求解病态反问题十分有效，在不少领域已得到成功应用，如热传导、地质勘探等。图2中给出了采用奇异值分解方法（图（c），（d））和正则化方法得到的重构图 （图（b）），其中图（a）为参考图。不难发现，不同的约束直接影响着重构图的质量。与SVD方法相比，通过正则化方法得到的图更接近参考图。

3 仿真分析

RSS值测量平台搭建：20个由TI公司制造的ZigBee无线节点部署在20.25 m2的平地上，每个节点沿着4.5 m的边长间隔0.9 m分开放置在距离地面1 m的位置上。无线节点工作在2.4 GHz频段上，并使用IEEE 802.15.4标准通信。系统中的节点采用轮询广播方式收发信息，扫描速率为3圈/秒。实验中采用木质立杆搭载无线节点，可以有效减小立杆对测量数据质量的影响。该平台的实景如图3所示。

图3 RTI系统网络布置实景图

RSS值测量获取：搭建上述平台后，在保证平台稳定工作的前提下，先让其处于空状态下工作30 min，并将所有接收到的RSS值保存在文件中，求其平均值yNULL。此后测试人员在一些固定的测试点上分别站立10 min，共得到650个可用数据 y（i）。Δy（i）=y（i）-yNULL便是后续实验所需的 RSS 值。在后续重构过程中用到的参数值见表1所列。RH为构造参考图时选用的人体半径。

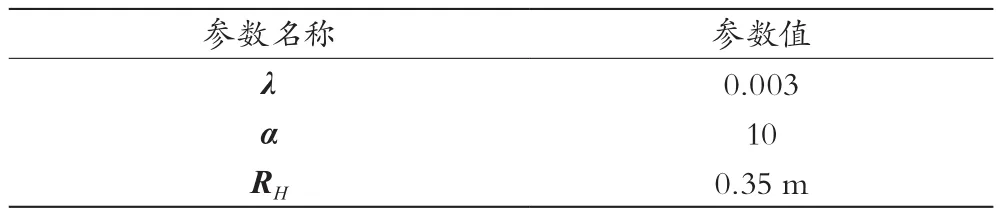
表1 图像重构参数

通过分析算法运行时间可得到图4。相比于非线性算子对应的TV正则化方法，在计算时间上Tikhonov正则化占据着绝对优势，且随着重构图尺寸的增大，后者完全可满足实时性要求，TV正则化方法的计算时间会随着图像尺寸的增加呈指数增长。

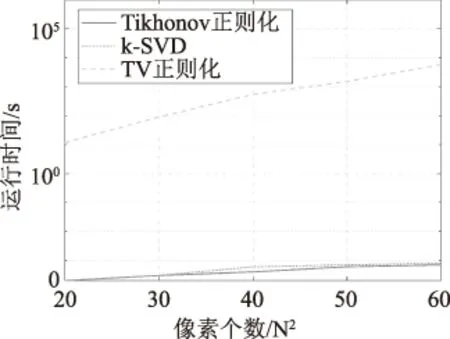
图4 三种算法运行时间比较

图像质量与RTI系统性能紧密关联，它的好坏直接影响着人的主观视觉。在RTI定位系统中，图像中位置亮斑与噪声亮斑之间的相对大小及位置即图像质量好坏的直接体现。一般地，信号质量评估指标均方误差（Mean Square Error，MSE）此时将失效，所以本文采用结构相似性度量（Structural Similarity Index， SSIM）作为图像质量评价指标[11-13]。三种算法下图像质量随像素尺寸变化的趋势如图5所示。

在RTI定位系统中，依据最大值定位准则（将图像中亮度值最大的位置作为目标位置）可不依赖人眼得到目标位置。在这种客观的定位方法中，明显处于劣势。三种算法定位精度与可靠性比较分别如图6、图7所示。从图6和图7中可以看出，奇异值分解法在定位精度和系统可靠性方面都不及正则化方法。此时，TV正则化方法在定位精度和系统可靠性方面都优于剩余两种方法。

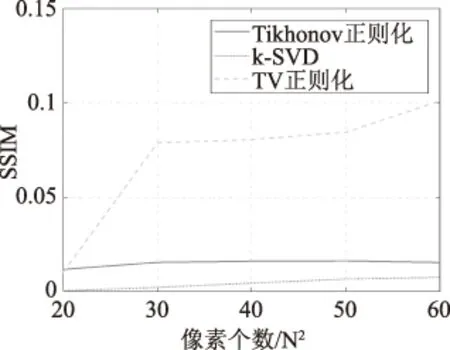
图5 三种算法所得重构图质量比较

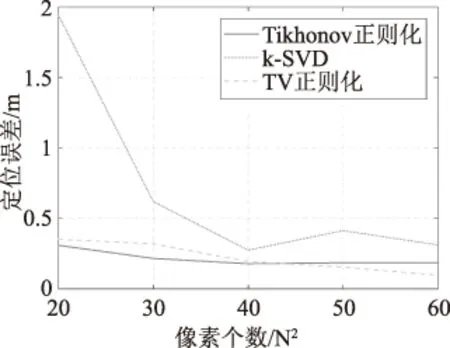
图6 三种算法定位精度比较

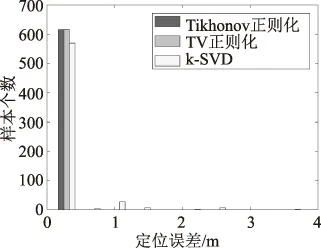
图7 三种算法定位可靠性比较

4 结 语

物联网技术的发展促进了RTI技术的深入研究，选取适当的重构算法有利于该技术的推广。本文对三种典型重构算法进行了仿真实验，仿真结果表明：不存在绝对完美的RTI重构算法，线性算子有利于降低计算时间，非线性算子有利于提高图像质量和系统性能。实际应用中可根据特定应用场景选取恰当的RTI重构算法，以利于节省资源。

[1]汪苑，林锦国.几种常用室内定位技术的探讨[J].中国仪器仪表，2011（2）：54-57.

[2]李同松.基于ZigBee技术的室内定位系统研究与实现[D].大连：大连理工大学， 2008.

[3]顾晶晶，陈松灿，庄毅.基于无线传感器网络拓扑结构的物联网定位模型[J].计算机学报，2010，33（9）：1548-1556.

[4] WILSON J， PATWARI N. Radio tomographic imaging with wireless networks[J].IEEE transactions on mobile computing， 2010，9（5）：621-632.

[5] WILSON J， PATWARI N， VASQUEZ F G. Regularization methods for radio tomographic imaging[Z]. Virginia tech symposium on wireless personal communications， 2009.

[6]王满意.基于无线传感器网络的无线层析成像定位技术的研究[D].北京：中国矿业大学， 2015.

[7] KANSO M A， RABBAT M G. COMPRESSED RF Tomography for wireless sensor networks：centralized and decentralized approaches[C]// IEEE international conference on distributed computing in sensor systems. springer-verlag， 2009：173-186.

[8] YANG L， HUANG K， WANG G， et al. An enhanced multiscale model for shadow fading in radio tomographic imaging[C]//Intelligent control and automation. IEEE， 2015：5925-5930.

[9] KE W， WANG T， SHAO J. CS-based device-free localization in the presence of model errors[C]// IEEE International conference on acoustics， speech and signal processing. IEEE， 2016：4443-4447.

[10] HAMILTON B R， MA X， BAXLEY R J， et al. Propagation modeling for radio frequency tomography in wireless networks[J].IEEE journal of selected topics in signal processing， 2014，8（1）：55-65.

[11] SAVAZZI S， SIGG S， NICOLI M， et al. Device-Free radio vision for assisted living： leveraging wireless channel quality information for human sensing[J]. IEEE signal processing magazine， 2016， 33（2）：45-58.

[12] WANG Z， BOVIK A C， LU L. Why is image quality assessment so difficult？[C]// IEEE international conference on acoustics，speech， and signal processing. IEEE， 2002：IV-3313-IV-3316.[13] WANG Z， BOVIK A C. Mean squared error： Love it or leave it？A new look at signal fidelity measures[J]. IEEE signal processing magazine， 2009，26（1）：98-117.