航空发动机公差分析及分配方法研究

李 敏

（中国航发商用航空发动机有限责任公司，上海201108）

0 引言

目前国内航空发动机的公差设计与分析依然基于传统的方法，以一/二维尺寸链为主，分析对象仅限于尺寸和位置公差，且各零件的公差类型与公差值的确定和装配公差分析仍然采用手工方式，主要取决于设计人员的相关知识和经验，装配质量难以得到保证，也难以满足航空发动机的发展要求。

随着形位公差的日益推广和应用，以及产品功能要求的不断提升和扩展，公差分析技术，尤其是三维偏差分析技术，在过去20年间已得到了极大的发展。公差表达模型的发展，从无到有，从简单到复杂。矢量化和几何化的特征变动描述，准确地体现了公差本身的意义。为提高航空发动机产品设计与制造质量、缩短研发周期和降低开发成本，GE、西门子、阿尔斯通、罗罗

等公司高度重视几何尺寸公差设计和装配精度控制，相关专业部门均成立尺寸工程师团队协调负责，投入大量人力财力建设其试验数据库[1]。且各大OEM自行编制了大量航空发动机产品型号的几何形位公差技术规范标准，已成为各公司独自占有或专利垄断的商业秘密。

近些年来，各种各样的计算机辅助偏差分析软件已经广泛应用于航空、汽车和电子等各个行业，也推动了各个行业设计和制造技术的快速发展。目前来说，应用较为广泛的软件主要包括VSA、CETOL和3DCS，其计算原理均为基于蒙特卡罗方法仿真[2]，可以区分和量化以往被忽略的形位公差，如方向和形状公差，在得到精确结果的同时，也方便了公差优化分配。本文主要介绍使用西门子公司的偏差分析软件VSA对发动机结构开展公差分析和分配[3]。

1 航空发动机典型连接结构

航空发动机结构特征明显，刚性大，且多为回转体结构。转子/静子间采用止口定心，螺栓连接，常见结构方案如图1所示。

航空发动机中典型零件为机匣、盘和鼓，装配过程就是机匣、盘和鼓的堆叠，如图2所示。

对于典型零件A，通常情况下，主基准一般设置为前安装边上面积最大的平面，即图中的基准面A，并设置A面的平面度；第二基准通常为前安装边上面积较小的圆柱面，即图中的基准面B，并设置B面相对于A面的垂直度。对于后安装边，通常设置平面相对于主基准面和第二基准的跳动或平行度；同时，设置圆柱面相对于主基准和第二基准的跳动，典型零件B则采取相同原则。

图1 常见的航空发动机转静子连接方案

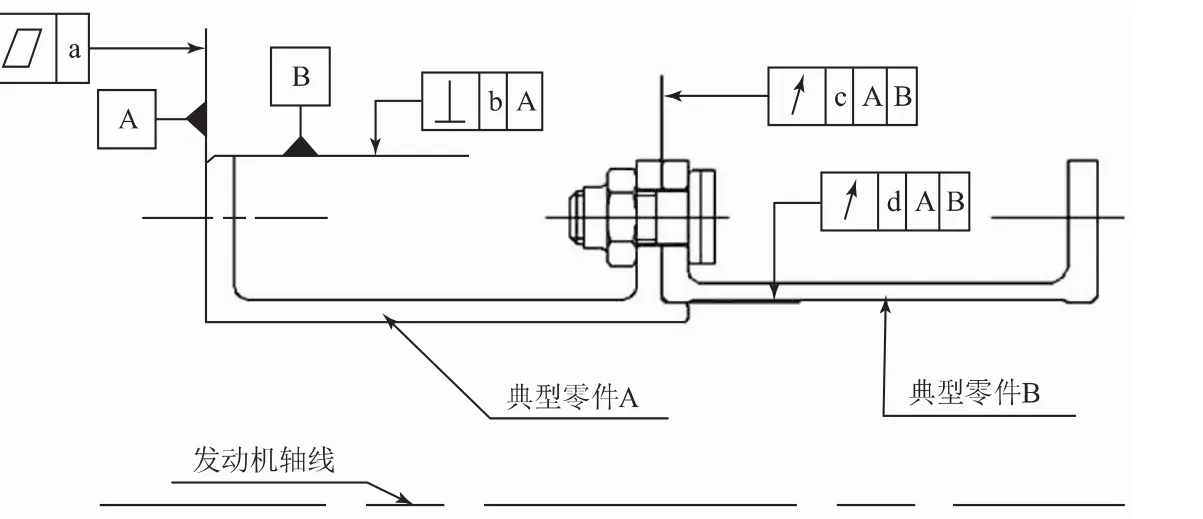
图2 回转结构公差设置

2 公差分析及分配

航空发动机公差分析及分配研究，使得在概念设计阶段就能综合考虑后续加工制造及装配质量问题，为发动机零组件公差设计提供输入，避免人为凭经验判断。

通过尺寸分析软件VSA开展装配偏差仿真，分析各部件接口尺寸和形位公差对最终产品几何精度的敏感度及贡献率，结合加工、装配、测量工艺分析，对发动机的设计公差、定位基准等进行优化，建立尺寸和形位公差分析及分配优化方案，最终提炼出航空发动机公差分析及分配流程，如图3所示。

2.1 关键尺寸控制要求及要素确定

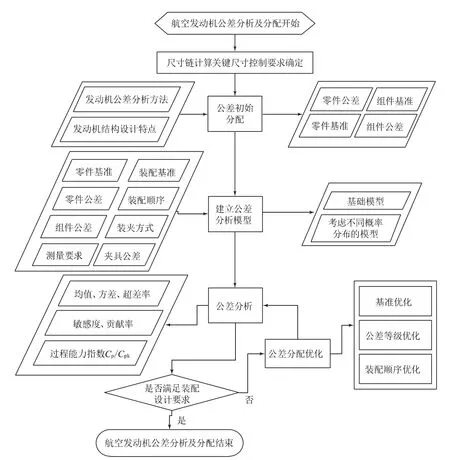
图3 航空发动机公差分析及分配流程

确定关键尺寸控制要素及要求，以明确公差分析对象，为计算设定分析目标。通过翻阅OEM维修手册及调研目前在研发动机尺寸控制需求，整机级尺寸控制主要包括：

（1）转静子间隙测量要求；

（2）封严间隙测量要求；

（3）轴向间隙测量要求；

（4）同轴度测量要求；

（5）轴承装配参数测量要求；

（6）安装检测要求。

以安装检测要求为例，高压转子同轴度检测，CFM56-3测量篦齿盘盘心跳动量，要求跳动量不大于0.038mm（0.0015inch）；GE90跳动值不大于0.05 mm，如果超差，需将高压涡轮转子重新装配到高压压气机上。

2.2 公差初始分配

航空发动机公差初始分配通常可采用极值法、统计法、蒙特卡洛法等。与传统的极值法和统计法相比，蒙特卡洛法在解决三维尺寸设计方面具有一定的优越性。该法在进行公差分析时，把求解封闭环尺寸及其公差的问题，当作求一个随机变量的统计量的问题来处理。

由于尺寸链中各组成环的尺寸是在产品零件加工过程中得到的，其数值是在其公差范围内并符合一定分布规律的随机变量。尺寸链方程决定的封闭环尺寸，则是一组组成环尺寸的随机变量的函数，所以它也是一个随机变量。

因此，封闭环尺寸及其公差的确定，完全可以采用随机模拟和统计试验的方法，在一定条件下，用这种方法得到的结果比较符合实际情况[3]。

2.3 建立公差分析模型

使用VSA软件建立整机公差分析模型。首先使用CAD软件进行实体建模，将零件实体模型转换成*.jt格式文件，其包含了与公差分析有关的全部GD&T信息，然后将*.jt文件导入VSA软件，在VSA软件中设置的参数包括图纸参数输入及装配工艺输入[4]。

前者主要包括零件基准、零件公差、组件公差及测量要求，即可参考图2的公差设置方法定义初始公差分配结果。后者主要包括装配基准、装配顺序、装夹方式及夹具公差，以图4的高压涡轮转子部件为例，输入要素包括测量基准A1、左边测量端、装配顺序（从右往左）、虚拟夹具以及引入的夹具公差。

依据航空发动机整机结构特点及装配性要求，输入相应参数，建立整机三维公差分析模型，模型示意图如图5所示。

2.4 公差分析

VSA软件可采用多种形式的表格和图形来输出公差分析的结果，例如均值、方差、合格率、敏感度和贡献度等信息，图6所示分别为软件计算后得到的统计直方图和各组成环的贡献率、敏感度列表。

图4 装配工艺输入

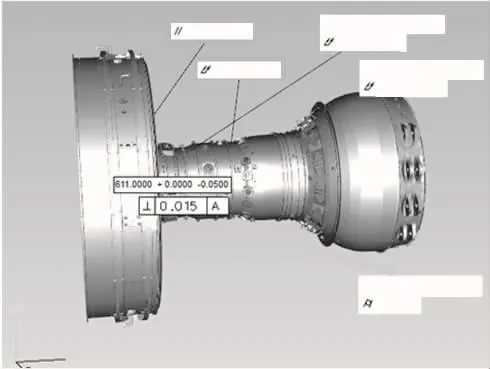
图5 整机公差分析模型示意图

直方图用于判断合格率是否满足要求，因VSA软件采用随机抽样的蒙特卡洛原理，存在所有公差都为极值的恶劣情况且软件中未有考虑形位公差的周向分布和相位信息等，通常航空发动机产品要求合格率≥70%。

图6 VSA软件输出的公差分析结果

根据敏感度和贡献率信息可完善公差分配，优化敏感度/贡献率较高的零件公差。通常重要件的公差等级选取5～6级，其他可选取7～8级；对于盘/轴类的几何形位公差加工精度要求较高，通常取端面平面度为0.02～0.04 mm，柱面相对于端面垂直度为0.01～0.03 mm，后端面相对于前基准的跳动要求为0.02～0.05 mm。

通过逐步调整各组成环的零组件公差及相应的VSA仿真，反复迭代，在满足合格率基础上可实现公差的优化分配[5]。

2.5 公差分配优化

因公差分析及分配结果受装配基准、测量基准、零组件精度等级、装配顺序等影响，以下对上述因素的优化原则加以细述：

（1）装配基准优化：整机装配基准应与设计基准相一致，以利于在装配过程中保证转静子轴向、径向间隙；整机装配基准应具有足够的刚性且为转、静子轴向尺寸控制的基准点。针对双转子航空发动机，为便于整机装配，装配基准通常设置在发动机主承力框架上。同时，整机装配基准也应遵循零件基准设计原则，选择端面作为装配的第一基准，装配过程中首先保证止口端面间的接触，保证止口端面的刚度，避免因为定位基准变形而造成定位失效。

（2）测量基准优化：调整测量基准的目标是达到基准一致性，测量基准应当同设计基准、装配基准尽量保持一致，防止基准变换引入不必要的误差。

（3）精度等级优化：应综合考虑零件加工成本与产品合格率，其设计过程可以采用以上步骤作为零件公差等级初始设计与验证的方法，该方法对零件公差初始设计具有一定的指导意义[6]。

（4）零组件精度等级优化：对于零组件公差精度等级设计，应综合考虑零件加工成本与产品合格率，以VSA软件输出的敏感度和贡献率为参考来确保某些关键位置的公差要求和功能需求。

（5）装配顺序优化：装配顺序也是影响装配质量的重要因素之一，在航空发动机的实际装配过程中，一般是零件先组装成组/部件，部件合格后再组装成整个单元体直至整机。因此，在进行VSA仿真计算时需要结合实际的装配过程，将公差分析模型分解成组/部件级来进行分析。

3 结语

通过三维偏差分析技术，建立航空发动机尺寸与形位公差分析模型，可为公差设计及分配提供可量化的输入，避免人为凭经验判断、设计/加工/装配的反复迭代，可在概念设计阶段综合考虑尺寸/形位公差、设计基准、装配基准、装配顺序、装配精度等对最终装配结果的影响，使得在概念设计阶段就能考虑和解决后续的制造质量问题，对设计和工艺进行优化。

[1]LIN E E,ZHANG H C.Theoretical Tolerance Stackup Analysis Based on Tolerance Zone Analysis[J].International Journal of Advanced Manufacturing Technology,2001,17(4):257-262.

[2]王晶，石宏，黄笑飞，等.基于蒙特卡罗模拟法的航空发动机装配公差分析[J].沈阳航空工业学院学报，2010，27（4）：8-11.

[3]张博，霍枫，张清，等.一种基于Vis Mockup的尺寸偏差分析方法[C]//第十五届中国科学技术协会学会第13分会场：航空发动机设计、制造与应用技术研讨会论文集，2013.

[4]单福平.航空发动机转子结构的装配偏差建模分析与工艺优化[D].上海：上海交通大学，2015.

[5]朱彬，于乃江，孟祥海，等.航空发动机装配尺寸链公差设计方法研究[J].测试技术学报，2015，29（2）：177-184.

[6]杨颖，汪劲松，郁鼎文，等.制造系统中的公差与成本[J].制造技术与机床，1999（5）：13-14.