基于电压闭环的异步电机弱磁控制研究
李长兵
(广州数控设备有限公司,广东广州510006)
0 引言
感应电机具有转子结构坚固、成本低、调速范围宽等优点,其传统的控制算法容易产生过大磁链,且无法提供最大转矩输出[1]。实际运用较多的查表法,通过查表对磁链进行控制,该方法对电机参数敏感,不具有通用性。电压闭环弱磁方案为近年来较为流行的算法,具有对电机参数敏感度低及鲁棒性强的优点,但仍存在如何最大限度利用直流母线电压的问题。
本文通过建立感应电机稳态数学模型,研究分析了电机全速度范围电流、电压约束条件,在电压闭环弱磁方案的基础上,提出了一种考虑转矩电流分量的弱磁控制策略,通过减小励磁电流提高系统的动态特性,使系统具有更好的跟踪特性。
1 感应电机数学模型
在理想条件下,当电机运行在高速状态,且忽略暂态量及定子电阻分量,电机模型可简化为:

式中,usd、usq为定子电压的d、q轴分量;isd、isq为定子电流的d、q轴分量;ωe为同步角速度;Ls为定子电感;σ为漏感系数,σ=1-Lm2/(LsLr),Lr为转子电感,Lm为互感。
电磁转矩为:
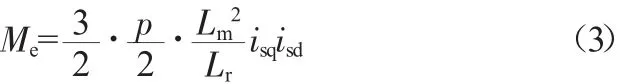
式中,p/2为极对数。
2 感应电机的弱磁控制算法
感应电机高速运行时,能提供给电机的最大电压受逆变器容量的限制,同时还受到电机允许输出最大电流的限制,因此电压、电流约束条件如下:

式中,usmax与直流母线电压和PWM调制策略有关,本文采用SVPWM调制,取usmax=udc/;ismax为电机长时间运行定子所能承受最大电流,一般取1.5~2倍额定电流。
将式(1)、(2)代入(4)、(5)中得:
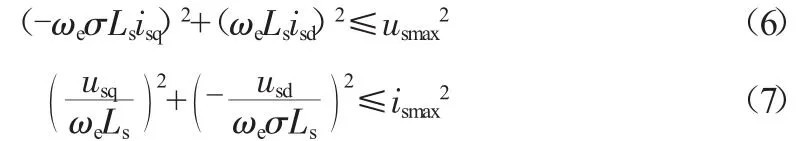
由式(6)、(7)可得到在直角坐标系构成的电流限制圆和电流限制椭圆,如图1所示。电机运行时电流轨迹始终在电流限制圆与电流限制椭圆的重合面积之内。此外,随着转速的增加,椭圆面积不断减小。
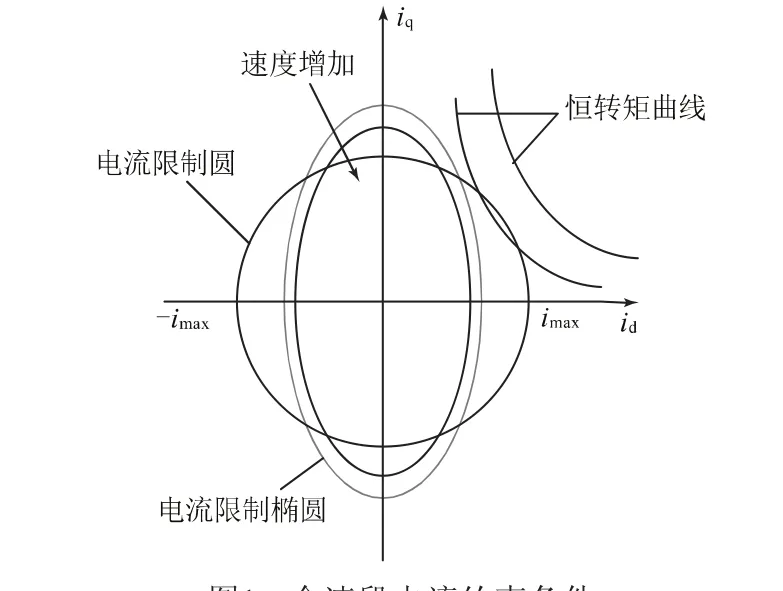
图1 全速段电流约束条件
由式(4)、(7)可得到在直角坐标系构成的电压限制圆和电压限制椭圆,如图2所示。电机运行时电压轨迹始终限制在二者重合的面积内。此外,随着转速的增加,椭圆面积不断增大。

图2 全速段电压约束条件
由式(6)可知,随着转速升高,电机升速需要的电压将超过umax,由于受最大电压的约束,可以通过降低励磁电流isd来使电机继续升速。
3 基于电压闭环的异步电机弱磁策略
弱磁算法的核心是如何控制励磁电流的给定。传统的电压闭环弱磁算法的思想是将电机升速所需的参考电压uref与umax相比,当uref>umax时说明系统已无法提供更大电压,需降低励磁电流,反之则应加大励磁电流,这可以通过一个PI调节器实现。考虑到电机正常运行的磁链给定,需对励磁电流进行限幅处理[2]。图3为传统电压闭环弱磁算法的控制框图,采用传统电压闭环弱磁算法时,随着转速的上升,q轴电压迅速增加,导致转矩电流反馈值减小,从而降低了q轴电流的动态特性;同时,d轴电压裕量的不足,使得d轴电流的动态性能较差,恶化了整个系统的动态性能。本文采用的方法是在传统电压闭环弱磁算法的基础上,通过改变励磁电流的给定使励磁电流和转矩电流的分配更加合理。励磁电流由弱磁PI控制器的输出与q轴电流跟踪误差函数fΔisq同时给定,使得q轴电压usq达到饱和状态时q轴电流仍能快速跟踪给定,原理如图4所示。
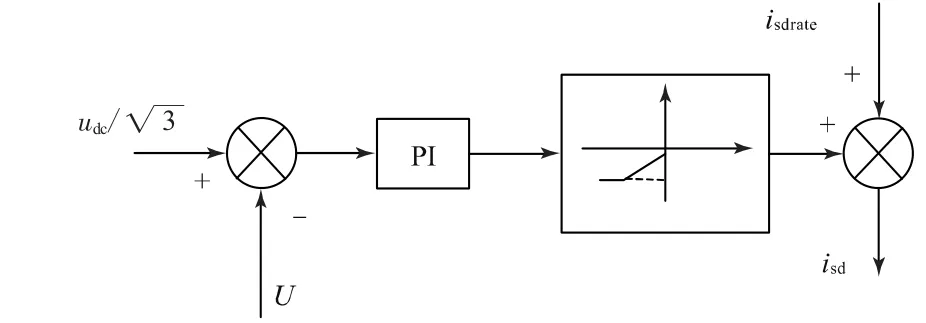
图3 传统电压闭环弱磁控制方法
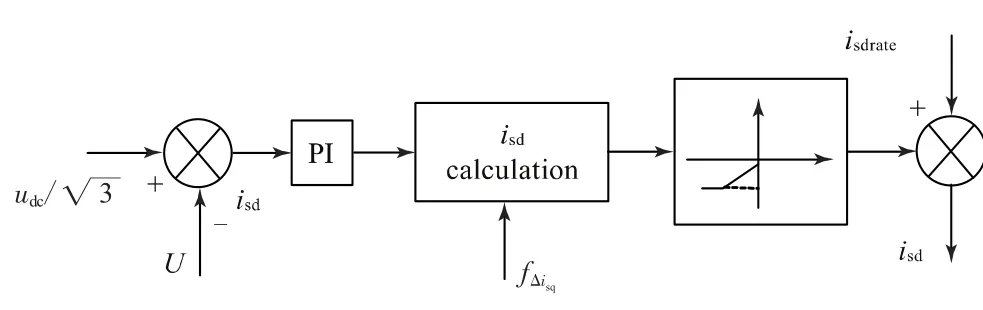
图4 本文采用方法
参考励磁电流的计算如式(8)所示:

式中,isd_ref为参考励磁电流;fΔisq为q轴电流跟踪误差函数;fΔisq为q轴电流跟踪误差;isq*为参考q轴电流。
异步电机弱磁控制系统框图如图5所示。
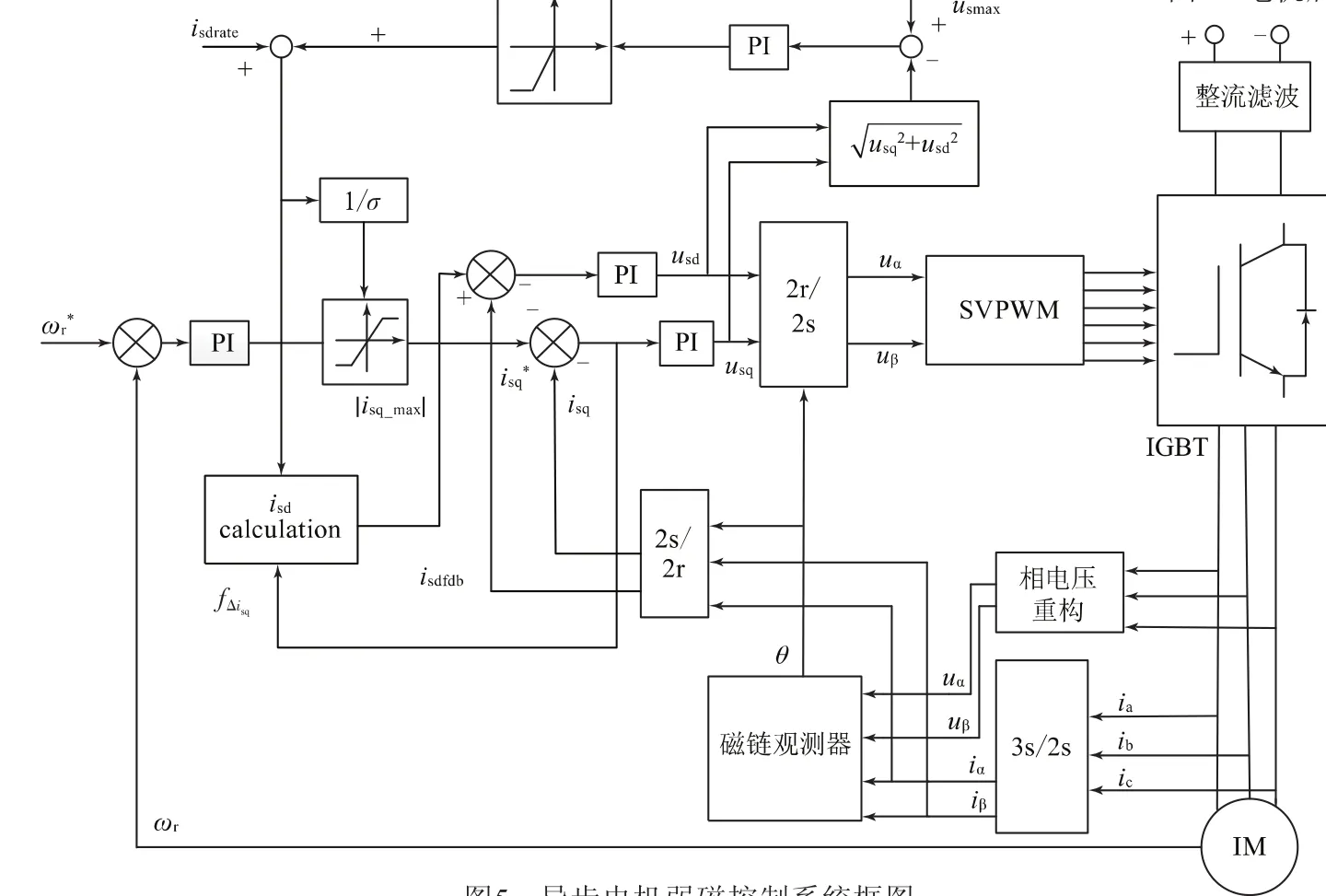
图5 异步电机弱磁控制系统框图
4 仿真结果及分析
仿真所采用的感应电机参数如下:额定电压UN=340 V,额定电流IN=13 A,额定功率PN=5.5 kW,额定频率fN=50 Hz,额定转速nN=1 000 r/min,最高转速nmax=7 000 r/min,极对数p/2=2,额定转矩TN=30 N·m,转动惯量为0.002 kg·m2。
图6为采用传统电压闭环方法和本文改进算法进行弱磁控制时速度波形的对比,给定速度为500 r/s,其中下方为改进算法得到的速度波形,通过比较可知,改进算法速度响应更快,动态性能更佳。
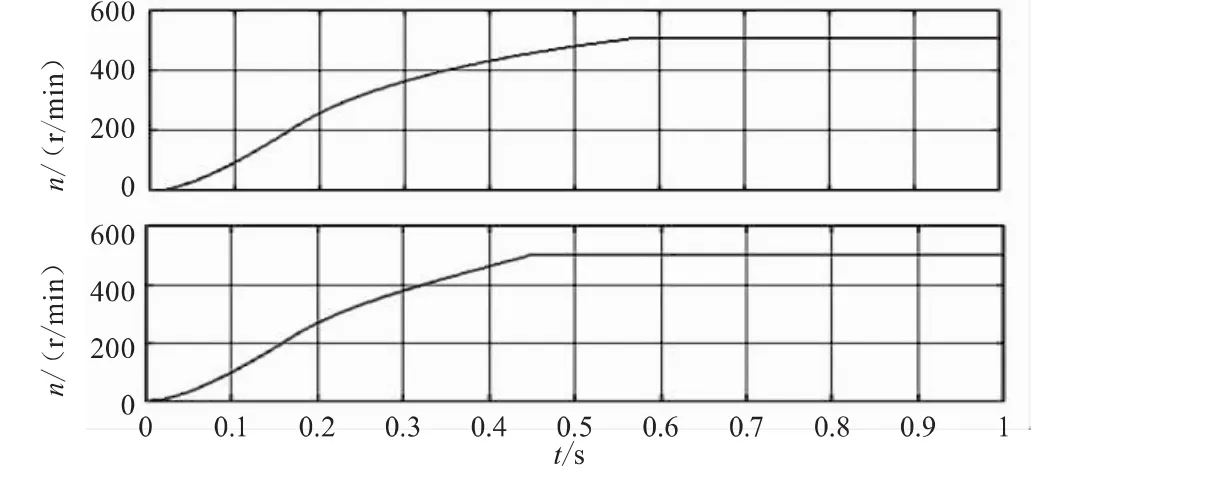
图6 速度波形对比
图7 为采用传统电压闭环方法和本文改进算法进行弱磁控制时的d轴励磁电流波形对比,其中下方为本文采用的改进算法,可以看出,本文采用的改进算法得到的励磁电流波形相对平滑,使电流的动态响应性能得到了改善。

图7 电机启动过程相电流和励磁电流给定曲线
5 结语
本文提出的改进算法,相比传统的电压闭环方法,能有效改善传统电压闭环弱磁方法在弱磁区动态性能下降的问题,响应速度更快。该算法结构简单,易于工程实现。
[1]XU X Y,NOVOTNY D W.Selecting the flux refence for induction machine drives in the field weakening region[C]//Conference Record of the 1991 IEEE Industry Application Society Annual Meeting,1991:361-367.
[2]万山明,陈骁.感应电动机转子磁场定向下的弱磁控制算法[J].中国电机工程 学报,2011,31(30):93-99.

