数值模拟分析灌浆缺陷对灌浆套筒连接力学性能的影响①
,
(同济大学土木工程学院,上海 200092)
0 引 言
在建筑工程领域,钢筋灌浆套筒连接主要应用于装配式混凝土结构中预制柱、剪力墙的竖向钢筋对接以及预制梁的水平钢筋连接。灌浆套筒常预埋在竖向预制混凝土构件底部,连接时在灌浆套筒中插入带肋钢筋后注入灌浆料拌合物,通常认为当灌浆料从溢浆孔溢出时则灌浆完全。但在实际工程中,出于某些原因,可能出现灌浆料未完全填充套筒就从溢浆孔溢出的情况,此时若停止灌浆,已注入的灌浆料在本身的流动性和重力作用下成形、凝结、硬化,从而套筒内部出现脱空。水平连接和竖向连接成形方式不同,灌浆料的成形也不同:对于水平连接,将出现水平套筒全长范围内的顶部脱空;对于竖向连接,套筒底部灌浆料密实,套筒顶部完全脱空,即上侧连接钢筋的锚固长度将减小。
根据标准[1],套筒形成接头的抗拉强度和变形性能应符合[2]中Ⅰ级接头的规定,即抗拉强度等于被连接钢筋的实际拉断强度或不小于1.10倍钢筋抗拉强度标准值。套筒内壁设置了多道环肋构造,大大加强了灌浆料与套筒间的机械咬合性能。从文献[3]中试验亦可观察到,滑移主要发生在钢筋与灌浆料之间,且在发生破坏前,滑移量较小,试件最终发生钢筋与灌浆料间的粘结破坏。故假定灌浆料与套筒之间粘结完好,无滑移产生,仅建立考虑钢筋与灌浆料之间粘结滑移关系的模型进行分析,并比较模型结果与试验结果。基于上述模型,采用有限元软件ABAQUS对单调拉伸加载试验[3]进行模拟,进行模型的试验验证,在此基础上进行连接的优化分析。
1 模型处理
1.1 材料模型
(1) 灌浆料
关于灌浆料的应力应变关系尚无成熟的理论模型。灌浆料与水泥砂浆有一定的相似性,以水泥砂浆的本构模型为基础,通过修改其中的某些系数来建立灌浆料的本构模型。
文献[4]中提到,砂浆强度越大,应力应变上升段曲线越陡,即弹性模量越大。但灌浆料的强度远大于一般砂浆的强度,其弹性模量相对强度增加地慢。所以将上述文献中曲线上升段的方程式修改为:
(1)
式中:σ为应变为ε时砂浆的应力;fc为峰值应力,取实测砂浆抗压强度;ε0为相应于峰值应力时的应变,取实测值;εu为极限压应变,取峰值应变的1.5倍。
抗拉应力应变关系采用双线性模型,开裂前采用线弹性模型,强度采用抗拉与抗压弹性模量相等;开裂后单轴本构关系采用线性软化模型,软化模量根据断裂能准则计算。由于灌浆料粒径相对较小,将欧洲模式规范MC90[6]中灌浆料断裂能计算公式的α取0.02。
(2)钢筋
钢筋采用具有明显流幅的软钢,本构关系采用理想化的三折线模型。弹性模量、屈服强度、屈服平台长度及极限强度根据对照试验确定,泊松比ν取0.3。
(3)套筒
套筒材料模型采用理想弹塑性模型,根据规范[6],屈服强度不小于370MPa,取对照试验实测值483MPa,弹性模量取2.1×105MPa。
1.2 粘结滑移模型
灌浆套筒连接中,钢筋、灌浆料和套筒三者之能协同工作,在于它们之间较好的粘结作用。考虑到灌浆料和混凝土同属水泥基质材料,力学性能相近,可近似地认为钢筋与灌浆料之间的粘结破坏机理和钢筋与混凝土之间的破坏机理大致相同。
对灌浆不充足的连接,竖向连接的套筒尚能充分发挥其约束作用,水平连接由于纵向脱空部分的存在,钢筋与灌浆料之间的粘结强度因灌浆料的含量不同而不同层次地被削弱,在对照试验中,连接均发生钢筋与灌浆料之间的粘结破坏。所不同的是,竖向连接的粘结应力达到峰值时,均发生钢筋的刮犁式拔出破坏,周围灌浆料表现完好,并未破碎;水平连接的粘结应力达到峰值时,均发生灌浆料的劈裂破坏。因此,分别选取了适用于竖向连接和水平连接的粘结滑移本构模型。
(1)竖向连接的粘结滑移模型
文献[8~9]研究表明,当相对粘结长度增大时,粘结应力沿粘结段的分布趋向于不均匀,平均粘结强度降低。釆用徐有邻的公式[8]以及对照试验数据对Steuck[10]粘结滑移模型中的峰值应力进行修正。由于对照试验中仅在上侧钢筋的埋长发生变化,因此,根据徐有邻的钢筋埋长修正系数Kbl,提出了仅考虑钢筋埋长影响的粘结强度公式,如下:
(2)
式中,la为连接试件上侧钢筋的粘结长度;d为钢筋直径d=20mm。
(2)水平连接的粘结滑移模型
对于水平成形的钢筋套筒灌浆连接,在套筒顶部存在纵向条状脱空部分,此时钢筋上表面的灌浆料覆盖层可近似为保护层。在没有约束的情况下,钢筋与灌浆料之间的粘结强度会随着灌浆料覆盖厚度的增大而增大[8]。但由于套筒的存在,灌浆料含量增大的同时,与套筒的接触面积也增大,约束作用越明显,钢筋与灌浆料之间的粘结强度进一步增强。因此,钢筋与灌浆料之间的粘结强度是随着灌浆料含量的增大而增大的,灌浆料的含量通过钢筋上表面覆盖厚度c来反映,其中0 ≤c≤ 10mm。
文献[11]提出了一个改进的粘结滑移本构关系。模型中水平连接的钢筋埋长和灌浆料强度都是确定的,灌浆料含量是唯一的变量,因此对其公式进行修正。参照试验中的水平连接含两类,可通过图1看出粘结强度随灌浆料覆没厚度的变化趋势。

图1 粘结强度随灌浆料覆没厚度的变化
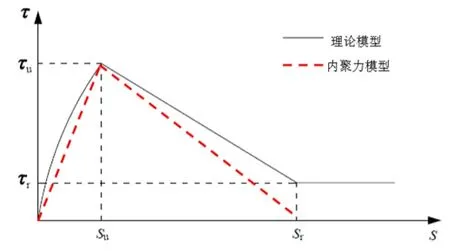
图2 水平连接内聚力单元模型参数确定
由图1可以看出,水平连接中,钢筋与灌浆料之间的粘结强度并非随着灌浆料覆没厚度的变大呈线性增长,而是先增长慢、后增长快,大致呈指数函数增长。因此,提出适用于水平连接中钢筋与灌浆料之间的粘结强度关于灌浆料覆盖厚度的关系式,如下:
(3)
式中,c为灌浆料覆盖厚度,取值0 ≤c≤ 10mm;d为受拉钢筋直径,取d=20mm;τ0为灌浆料覆盖厚度为0mm时的粘结强度;K为套筒增强系数;a为灌浆料增强系数。
将图1中的散点坐标代入到公式(3),得到公式如下: (单位:MPa):
τ=7.865+6.485×1.110
(4)
对于残余粘结滑移rs,参照CEB-FIP的建议,将0.5Cclear定义为残余粘结强度对应的滑移量,其中Cclear为钢筋助间距,为10mm,故sr为5mm。对于极限滑移值us和残余粘结强度r,文献[11]并未对提出确定方法。对于极限滑移值us,本文沿用Steuck模型对应参数。
(3)粘结滑移在有限元中的实现
采用ABAQUS中的内聚力单元模拟接触面的粘结滑移性能[12],最大名义应力准则作为初始损伤准则,并选择基于位移的损伤演化定义损伤演化规律,刚度退化方式为线性。对于竖向连接,内聚力单元的牵引分离本构模型参数根据Steuck模型确定。对于水平连接,内聚力单元的牵引分离本构模型参数根据文献[11]提出的公式确定,如图2所示。
1.3 模型简化处理
根据单调拉伸对照试验中套筒连接的破坏形式,套筒与灌浆料之间粘结完好,发生钢筋与灌浆料之间的“刮犁式”剪切型破坏或者灌浆料劈裂破坏,本质上都是钢筋与灌浆料之间的粘结强度不够而破坏。中文的有限元分析,套筒和灌浆料之间绑定在一起,钢筋与灌浆料之间的粘结滑移用内聚力单元模型模拟。内聚力单元与钢筋和灌浆料部件之间的界面也采用绑定。
2 数值模拟结果与分析
2.1 连接的模型结果
(1)破坏模式
将有限元分析所得的结果与试验结果做对比,如表1和表2所示。破坏模式的判定准则为:达到峰值荷载时,若钢筋应力达到极限强度并发生明显颈缩变形,则判断为钢筋拉断破坏;若钢筋应力小于极限强度,且钢筋相对灌浆料发生很大的滑移变形,则为连接的粘结破坏。
由表1可知,除了竖直方向第二组以外,其余所有的模型破坏模式和对照试验结果一样均为钢筋的拔出。竖直方向第二组模型破坏模式为钢筋的拉断,这和单调拉伸试验中的拔出破坏不一致。分析认为,该连接在标准养护条件下养护28d后,在单调拉伸试验中的粘结承载力平均值为189.33kN,钢筋材性试验的抗拉承载力平均值为193.32kN,后者比前者仅提高了0.21%,由ABAQUS模拟出连接的两种破坏形态,钢筋拉断破坏如图.3所示,钢筋拔出破坏如图4所示。
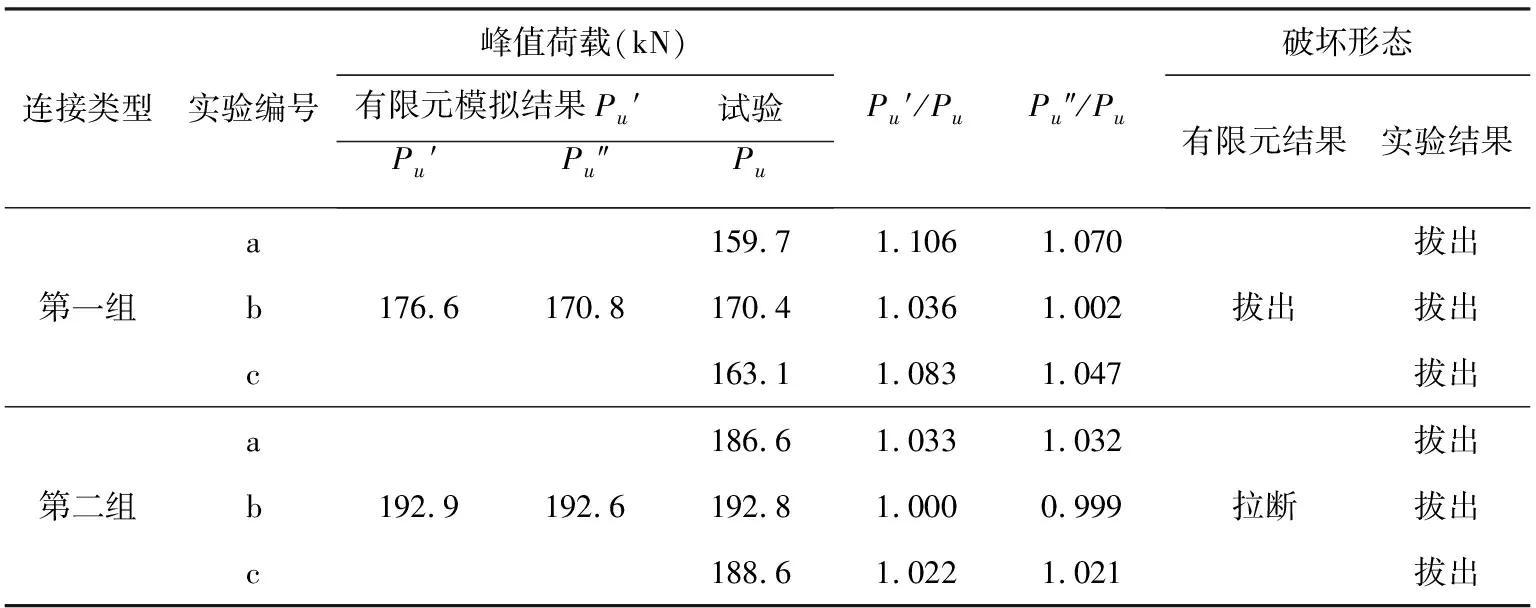
表1 竖直连接的有限元分析结果与试验结果对比
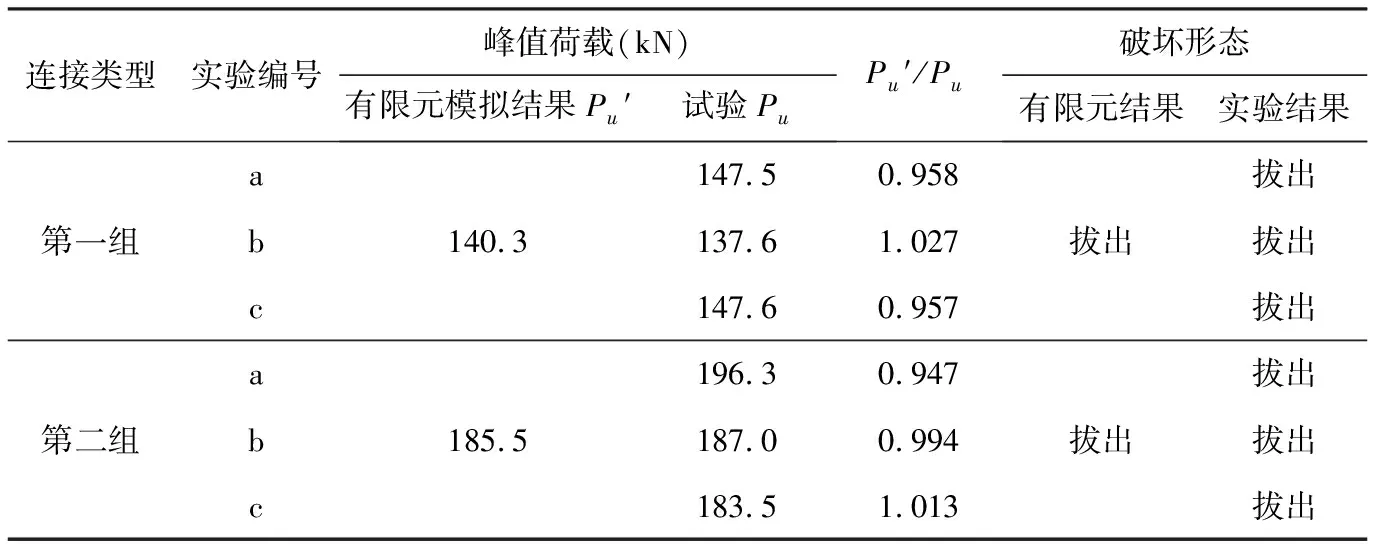
表2 水平连接的有限元分析结果与试验结果对比
(2)承载力
将有限元分析所得的结果与试验结果对比,对于竖向连接(表1),Pu′表示采用Steuck模型的有限元分析得到的极限荷载,Pu′表示采用修正后的Steuck模型的有限元分析得到的极限荷载;对于水平连接(表2),以Pu′表示有限元分析得到的极限荷载。Pu为试验得到的极限荷载结果,P为按钢筋拉断时的强度计算的理论承载力。由表可知,对于竖向连接,采用修正后的Steuck模型计算出的极限荷载比修正前的Steuck模型计算出的极限荷载更接近试验结果;对于水平连接,考虑灌浆料的塑性损伤,有限元分析得到的峰值荷载与试验劈裂破坏时的荷载接近。因此则按文中的分析方法能够提供符合精度要求的承载力结果。

图3 模型钢筋拉断破坏

图4 模型钢筋拔出破坏
(3)荷载位移曲线
图5和图6分别为各试件荷载变形曲线有限元结果与试验结果的对比。由图可知,各试件受拉荷载-变形曲线形状模拟结果与试验曲线基本相同。在钢筋屈服之前,有限元曲线与试验曲线基本重合;钢筋屈服之后,由于钢筋本构关系采用的是理想化的三折线模型,强化段为一条直线,而实际钢材的强化段为一条上凸的曲线,因此,在钢筋进入强化阶段后,有限元荷载变形曲线与试验曲线稍有差异,不过仍基本相符。
(4)套筒受力情况
典型的套筒应力分布如图7和图8所示。对于竖向连接,同一截面应力相同,且最大应力出现在钢筋端部位置的套筒截面;对于水平连接,同一截面应力不相同,最大应力出现在钢筋端部位置套筒上表面。无论竖向连接还是水平连接,在整个受力阶段,套筒应力最大值未超过 483MPa,处于弹性状态。故满足标准[13]规定的套筒在连接受力时是安全的。

图5 第二组水平连接套筒有限元模拟的荷载-位移曲线
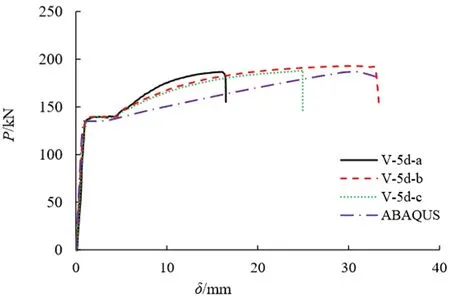
图6 第二组竖直连接套筒有限元模拟的荷载-位移曲线
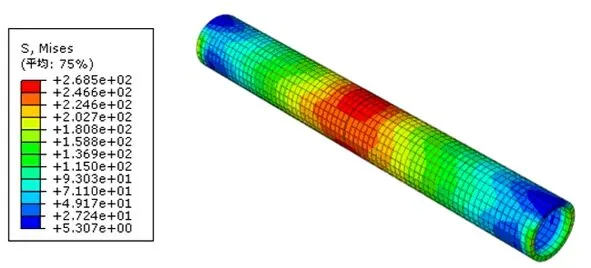
图7 第一组水平连接套筒应力分布
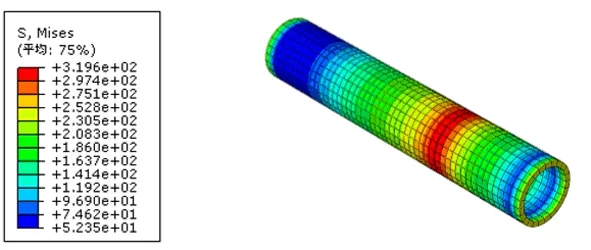
图8 第一组竖直连接套筒应力分布
2.3 安全控制指标分析
假定破坏模式必须为钢筋拉断破坏,基于对照试验结果,对常温下养护达到28d龄期的HRB400、d=20mm钢筋灌浆套筒连接进行安全控制指标分析。分析原则为:连接发生钢筋拉断破坏时,取灌浆料含量最少的情况。分析的方法为:钢筋、套筒和灌浆料材性保持不变,对竖向连接,以0.5d(即10mm)为步长,改变溢浆侧(上侧)钢筋在灌浆料中的埋长;对水平连接,以1mm为步长,逐步增加钢筋上表面灌浆料的覆盖厚度。
(1)竖向连接的安全控制指标分析
当灌浆料含量发生变化,溢浆侧钢筋在灌浆料中的埋也会发生相应变化,当溢浆侧钢筋在灌浆料中的埋长不足以使钢筋被拉断时,发生钢筋拔出破坏,随着溢浆侧钢筋埋长的增加,连接极限强度增加;当溢浆侧钢筋埋长增加到一定值时,破坏模式转变为钢筋拉断破坏,极限强度保持不变。本文规定,竖向连接的破坏模式恰好由钢筋拔出转变为钢筋拉断时的溢浆侧钢筋埋长为临界长度。部分结果如表3所示
表3不同上侧钢筋埋长的垂直连接破坏模式

编号L/d承载力F/kN破坏模式V-14170.84钢筋拔出V-25192.63钢筋拔出V-35.5192.91钢筋拉断V-46192.91钢筋拉断
当上侧钢筋在灌浆料中的埋长介于5d~5.5d之间时,竖向连接发生钢筋拉断破坏,此时承载力最大。因此,取5.5d为竖向连接发生钢筋拉断破坏的允许的最小上侧钢筋埋长。
(2)水平连接的安全控制指标分析
对于水平连接,灌浆料分布于套筒全长范围内,当灌浆料覆盖厚度不足时,发生钢筋拔出破坏,随着灌浆料覆盖厚度的增加,连接极限强度增加;当灌浆料覆盖厚度增加到一定值时,破坏模式转变为钢筋拉断破坏,极限强度保持不变。文中规定,水平连接的破坏模式恰好由钢筋拔出转变为钢筋拉断时的灌浆料覆盖厚度为临界厚度。模拟部分结果如表4所示。
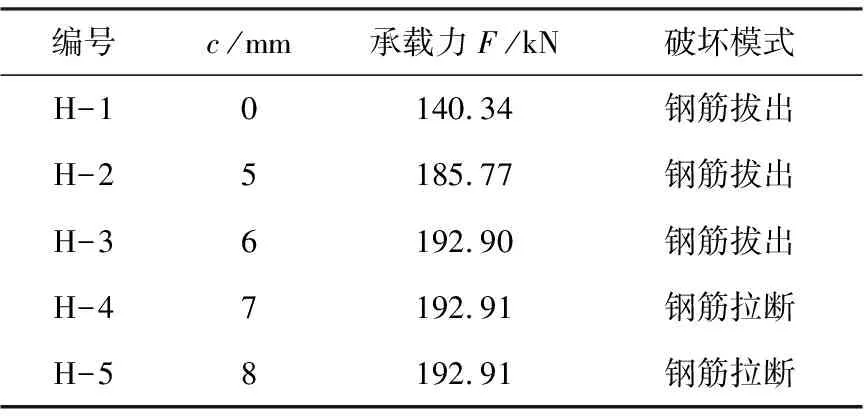
表4 不同上侧钢筋埋长的水平连接破坏模式
当灌浆料覆盖厚度介于6mm~7mm之间时,水平连接发生钢筋拉断破坏,此时承载力最大。因此,取7mm为水平连接发生钢筋拉断破坏的允许的最小灌浆料覆盖厚度。
5 结 论
基于通用有限元分析软件ABAQUS,对钢筋灌浆套筒连接的单调拉伸试验进行了数值模拟,得到以下结论:
1)在水平连接的数值模拟中,钢筋与灌浆料之间的粘结滑移模型考虑了灌浆料覆没厚度对粘结强度的增强作用,并提出了粘结强度修正公式,能较好地模拟出水平连接的承载力情况;
2)利用 ABAQUS 的内聚力单元模型模拟钢筋与灌浆料的粘结滑移作用,得到的承载力及变形结果与实际基本相符,能较准确判断其破坏模式和极限承载力,精度可满足工程要求;
3)套筒在连接受力过程中,始终处于弹性阶段,满足安全要求;
4)数值模拟结果与参照试验吻合良好,可用于进一步分析和研究;
5)初步得到使承载力达到最大(发生钢筋拉断破坏)的最少灌浆料含量,竖向连接中上侧钢筋锚固长度取5.5d;水平连接中钢筋上表面覆盖厚度为7mm。
参考文献:
[1] 中华人民共和国建筑工业行业标准.JG/T398-2012 钢筋连接用灌浆套筒[S].北京:中国标准出版社出版发行,2012.
[2] 中华人民共和国行业标准.JGJ107-2010 钢筋机械连接通用技术规程[S].北京: 中国建筑工业出版社, 2010.
[3] 王鑫.灌浆料含量对钢筋套筒灌浆连接力学性能的影响[D].上海:同济大学.2016.
[4] 朱伯龙.砌体结构设计原理[M].上海:同济大学出版社.1991.
[5] 中国建筑科学研究院.装配式框架梁柱节点力学性能试验研究报告[R].2012.
[6] 中华人民共和国国家标准.GB/T1348-2009 球墨铸铁件[S].北京: 中国标准出版社,2009.
[7] 张海顺.预制混凝土结构插入式预留孔灌浆钢筋锚固搭接试验研究[D].哈尔滨: 哈尔滨工业大学,2009.
[8] 徐有邻.变形钢筋—混凝土粘结锚固性能的试验研究[D].清华大学,1990.
[9] 徐有邻,邵卓民,沈文都.钢筋与混凝土的粘结锚固强度[J].建筑科学.1988.
[10] Steuck KP, Eberhard MO, Stanton JF.Anchorage of Large-diameter Reinforcing Bars in Ducts[J].ACI Structural Journals, 2009,106(S48):506-513.
[11] 孙铭.钢筋混凝土粘结滑移本构试验研究及有限元分析[D].杭州:浙江大学.2015.

