基于Petri网可行迹的系统变化定位方法研究

，

(安徽理工大学，安徽 淮南 232001)

0 引 言

目前，业务流程模型管理在各个业务领域中发挥着重要作用，将流程模型转化为工作流Petri网，能够将流程运行直观化，流程的变化也可以进一步被研究。文献[1]提出了一种从事件日志中挖掘可变的片段的方法，提出从事件日志中提取形态学片段的新算法以实现其组合性和灵活性。文献[3]提出了一组变更模式和变更支持特性，以促进系统对现有流程管理技术相对于变更支持的比较。文献[6]探究了流程模型之间的变化传播，并提出在一个模型中给定一个变化，之后利用对应活动的行为轮廓决定另一个模型的变化，指出引起异常行为的变化都能通过目标模型与源模型相比对的途径查找得出。文献[8]从变化分类角度来动态评估变化对整个流程系统的影响。使用 Petri 网对系统变化的研究大都集中在变化的检测与诊断上，本文从工作流Petri网出发，利用可行迹及变迁间的最小后继关系找出网系统中的变化，给出变化后的网系统。

1 基础知识

定义1[2](工作流Petri网) 一个网N=S,T;F,i,o称为工作流Petri网，当且仅当：

(1)该Petri网有唯一的源库所i:·i=φ；

(2)该Petri网有唯一的终止库所o:o·=φ；

(3)该Petri网上的每一个节点都属于i到o的一条路径上,即Petri网是强连通的。

定义2[5](标记工作流网)N=S,T;F,i,o为一个工作流网，∑为事件集合，标记函数λ:T→∑,M0为初始标识，则LWN=N,∑,λ,M0为一个标记工作流网。

定义3[7](行为轮廓) 设是一个网N,M0，初始标识为M0,对任给的变迁对t1,t2∈T×T满足下面关系;

(1)若t1≻t2且t2≯t1，则称严格序关系，记作t1→t2；

(2)若t1≯t2且t2≯t1，则称排他关系，记作t1+t2；

(3)若t1≻t2且t2≻t1，则称交叉序关系，记作t1||t2；

将所有关系的集合叫做网系统的行为轮廓，记作BP=→,+,||

定义4(可行迹) 一个过程模型所有活动的集合记为A，α∈A，活动α的执行为一个事件记为ε(ε∈εi)；一个可行迹是指一个能够发生的序列τ=ε1,…,εn，每个可行迹对应于一个过程的执行。

2 业务系统中的变化检测与诊断

2.1 模型假设

假设：1、假设所有变迁都有不为空的标记；2、业务系统N,Mi是合理的工作流网。

下面给出两种变化的定义：DELETE和MOVE。

存在网系统Σ，网系统Σ′由网系统Σ经过一系列的变化产生。

DELETE：在网系统Σ中，存在t∈T，在Σ′中活动t不存在，称这种变化为删除。

MOVE：在网系统Σ中存在t1→t2，在网系统Σ′中，有t2→t1；称这种变化为移动；此定义针对本文示例提出，因此具有单一性。

2.2 算法分析

下面以工作流网为研究背景，给出了基于可行迹及最小后继关系的系统变化定位算法。

算法1：工作流网中系统变化的定位算法(Changes Identification Algorithm for Workflow-Net system，简记为CIA算法)

输入：源模型Σ=S,T;F,M,一组行为事件迹，源模型最小后继关系矩阵；

输出：变化后的网系统Σ′。

步骤：

Step1：根据网Σ=S,T;F,M，计算最小后继关系；

Step2：通过给出的一组可行迹集合STrace，利用行为轮廓关系，即BP=→,+,||,计算minimalk-successorrelations，简称为R。

Step3R1：图1网系统对应的最小后继关系，表1所示；R2：可行迹的最小后继关系。

3.1比较R1，R2寻找后继关系不一致的变迁对ti,tj

(1)If∀t∈STrace，Rti,tj∈R1,Rti,tj∉R2,并且

R1ti,tj=R2ti,tj+1,ThenT′=T′-tjΣ=S′,T′;F′；

(2)IfR2ti,tj=R1tj,ti并且R2=tj,tmm≠j=R1ti,tmm≠i

ThenT′=∀t∈STrace|t=ti,tj=tΣ=S′,T′;F′。

2.3 举例说明

下面举例分析上述算法的实施步骤：首先给出一个过程模型和其对应的网系统。对系统变化进行定位分析，检测变化变迁，计算出存在变化的工作流网，画出对应的网系统，下面列举DELETE和MOVE两种变化检测来验证方法的可行性。

以BPMN语言对业务流程建模，A-H代表活动，X-Y代表事件。如图1所示：

图1 过程模型及其对应的网系统

针对图1所给出的网系统，列出变迁对之间的后继关系，不存在后继关系的变迁对用小黑点表示；若变迁对行为轮廓关系为||的后继关系为1，处于+的不存在后继关系。具体如表1所示：

表1 图1网系统对应的最小后继矩阵

接下来给出网系统的几组迹利用可行迹及变迁之间的最小后继关系定位变化变迁位置。下面给出网系统中的所有可行迹：[X,A,B,H],[X,A,C,D,H],[X,A,C,D,F,D,H],[X,A,C,G,H],[Y,A,B,H],[Y,A,C,D,H],[Y,A,C,D,F,D,H],Y,A,C,G,H此类变迁可以出现在同一条迹中，所以任何变迁对之间不存在排他序关系，又已知网系统中变迁对X,Y为排他序关系，因为其不同时出现在一条执行迹中；又有X,A,B,C,D,G,H,X,A,B,C,D,F,D,G,H,Y,A,B,C,D,G,H,Y,A,B,C,D,F,D,G,H,以变迁B,C为例，可以同时发生但又不出现在单独的可行迹中，这类变迁对之间的行为轮廓关系为||，相互之间最小后继关系为1。

利用这组迹计算变迁之间的最小后继关系，首先以变迁X为例，变迁X在前四条迹中都有发生权,并且变迁H的发生是在变迁B,D,G发生之后发生的，因此变迁B,D,G是变迁H发生的必要条件；而变迁X,A,C发生是变迁G发生的必要条件，同时X,A,C发生是变迁D发生的必要条件，变迁B的发生需要变迁X,A同时发生，因此存在σ0=X∧σ0+6=H因此其最小后继关系为6；同理，可以计算σ0=A∧σ0+4=H。分析给出的所有迹，变迁A,B,C,D,F,G相对于变迁X的最小后继关系分别为1，2，2，4，3；变迁B,C,D,F,G,H相对于变迁A的最小后继关系分别为1，1，2，3，2，5；依次类推，得出存在变化变迁网系统的后继关系矩阵如表2：

表2 存在变化的最小后继关系矩阵1

与表1给出的最小后继关系表比较得变迁H相对于其它变迁活动后继关系发生了明显的变化，联合网系统1变迁E未在任意一条执行迹中出现，变迁E的缺失导致了网系统的变化，由后继关系表可得出E为变化产生的位置，给出相应的网系统如图2所示，用虚线框来标注此类变迁。

图2 变化网系统1

图3 变化网系统2

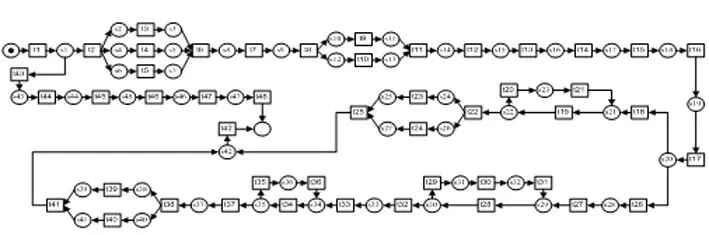
图4 某自动售票机Petri网模型

在网系统1中σ0=X,σ4=E,变迁E相对于X的后继关系为4，而在表2中，可以清晰的看到变迁E无发生权；所以变迁E的诊断最多可经过4个变迁的发生，即K=4。

同样地，已知一组迹：[X,A,B,H],[X,A,G,D,E,H],[X,A,G,D,F,D,E,H],[X,A,G,C,H],[Y,A,B,H],[Y,A,G,D,E,H],[Y,A,G,D,F,D,E,H],以变迁活动Y为例进行分析，类似于上述分析由存在变迁Y的后四条迹可得：Y→H存在7后继关系，变迁A,B,C,D,E,F,G,相对于变迁Y的最小后继关系分别为1，2，3，3，4，4，2；B,C,D,E,F,G,H相对于A的最小后继关系分别为1，2，2，3，3，1，6；又已知迹:[X,A,B,G,D,C,E,H], [X,A,B,G,D,F,D,C,E,H],[Y,A,B,G,D,C,E,H],[Y,A,G,D,F,D,C,E,H]；C,D,E,F,G,H相对于B的最小后继关系为1，1，1，1，1，1；依次类推，得出变迁之间的后继关系如表3。

表3 存在变化的最小后继关系矩阵2

与表1最小后继关系表作对比，可知变迁C参与的后继关系与变迁G参与的后继关系进行了交换，同时由可行迹变迁之间的行为轮廓关系可知C，G之间的执行顺序发生了交换，由C→G变为G→C,由此可以推断出存在变化的网系统。

在变化网系统中，σ0=X∧σ0+2=G,σ0=X∧σ0+3=C，所以最多分别经过2个3个变迁的发生能够诊断出执行关系发生变化的变迁G，C，即KG=2,KC=3。如图3：

3 实例分析

在实际生活中，把业务流程转化为Petri网模型，基于Petri网可行迹对网系统中的变化进行检测和诊断，能够有效地找出问题所在，为了验证所提方法的有效性，下面以一个自助售票系统为例，现某游客欲通过自助售票系统进行购票且为第一次购买，图4描述了某火车自助售票机的Petri网系统，其中每个变迁的含义如表4所示：

表4 图4变迁含义

某游客在购买火车票时可采取现金支付或银行卡支付两种支付方式，现某游客选择银行卡支付，在支付期间假设活动t38“支付完成”无法正常执行，系统显示为“支付失败”，我们利用可行迹的方法对问题进行检测，已知原网系统的可行迹为[t26,t27,t28,t29,t30,t31,t32,t33,t34,t35,t36,t37,t38,t39]给出一组迹[t26,t27,t28,t29,t30,t31,t32,t33,t34,t35,t34,t35,t38]，可以看出活动t34,t35,t34,t35发生了循环，在第一次密码错误，再次输入密码后，系统仍然提示错误；t34,t35重复执行了两次，所以导致了变迁t38无法正常执行，虚线框s37,t37表示的的库所和变迁不可见，t34,t35,t34,t35用红色虚线框进行标注。如图5所示：

图5 某自动售票机Petri网检测模型

4 结 语

基于工作流网系统中可行迹的执行，根据变迁对之间的minimalk-successorrelations，对比源过程模型网系统，检测并诊断变化变迁的位置，通过比对，给出存在变化变迁的网系统。未来关于系统变化的检测和诊断仍有很多问题需要研究，例如如何高效地对系统变化进行定位并改进，如何降低变化所带来的影响等。

参考文献:

[1] Pourmasoumi A, Kahani M, Bagheri E. Mining Variable Fragments From Process Event logs[J]. Information Systems Frontiers, 2016:1-21.

[2] Weidlich M, Mendling J, Weske M. Efficient Consistency Measurement Based on Behavioral Profiles of Process Models[J]. Software Engineering IEEE Transactions on, 2010, 37(3):410-429.

[3] Weber B, Rinderle S, Reichert M. Change Patterns and Change Support Features in Process-Aware Information Systems[J]. Data & Knowledge Engineering, 2008, 66(3):438-466.

[4] Weidlich M, Polyvyanyy A, Desai N, et al. Process Compliance Measurement Based on Behavioural Profiles[J]. Information Systems, 2011, 36(7):1009-1025.

[5] WEN LIJIE.Study on Process Mining Algorithm Based on WF Net[D].BeiJing: Tsinghua University.2007.

[6] Georg Grossmann, Shamila Mafazi, Wolfgang Mayer, et al. Change Propagation and Conflict Resolution for the Co-Evolution of Business Processes[J]. International Journal of Cooperative Information Systems, 2015, 24(01):33-40.

[7] Jensen M T. Improving Robustness and Flexibility of Tardiness and Total Flow-time job shops using robustness measures[J]. Applied Soft Computing, 2001, 1(1):35-52.

[8] Gupta C, Singh Y, Chauhan D S. A Dynamic Approach to Estimate Change Impact using Type of Change Propagation[J]. Journal of Information Processing Systems, 2010, 6(4):597-608.

[9] Kunze M, Weidlich M, Weske M. Querying process models by behavior inclusion[M]. Springer-Verlag New York, Inc. 2015.

[10] Küster J M,Gerth C,Forster A,et al.Detecting and Resolving Process Model Differences in the Absence of a Change log[C].Proceedings of the 6th International Conference on Business Process Management,Springer - Verlag,2008: 244 -260.