计算机科学中的算法设计与数据结构的离散性解析

高塔



计算机科学中的算法设计与数据结构的离散性解析

高塔

河北农业大学信息科学与技术学院，河北 保定 071000

主要探讨了计算机科学中算法设计与数据结构的离散性，用以对计算机问题的抽象解决进行具体化的解释，从而建立一种“连续性—离散性”的思维模式。

计算机科学；算法设计；数据结构；离散性；二进制

引言

计算机科学是一门包含多种与计算、信息处理相关的主题的系统科学，其由理论计算机科学、实验计算机科学组成[1]。在计算机科学中，计算机算法设计与数据结构是重要的基础知识，是计算机科学计算与模拟实验得以实现的工具，因此深入研究计算机算法设计与数据结构对计算机科学的发展具有重要意义。本文主要解析计算机科学中算法设计与数据结构的离散性问题。

1 算法设计的离散性

算法是对问题的解决的具体性完整性的方案描述，其代表了运用系统的方法对解决问题加以描述的策略机制。算法设计体现了计算机科学的离散性，其常用方法包括递推法和递归法。笔者主要探讨算法设计方法的离散性。

1.1 递推法

递推法是一种常用于序列计算机中的算法，其核心内容是重复复杂计算过程到简单计算过程的转化。

按照递推法的定义，计算机采用了一种笨办法来实现复杂的运算，比如求最大值的算法。根据求最大值的算法，计算机会反复比较最大的已知数字和数组中的下一数字，直至结束。与此相比，人类采用了完全不同的方式进行数值大小的比较，即当数字较多时，先确定数字的位数，再选定位数最高的数字；若该类数字的个数较多，则需逐一比较。这种思维模式是人类惯用的连续性思维。对此，计算机很难运用这种连续性思维，而需设计复杂的算法来“模拟”这一连续性思维。另外，可能存在下列可能性：人类的大脑较为高级及其算法非常复杂，因此具备连续性的思维[2]。

1.2 递归法

递归法是指一个函数或过程在说明或定义中间接或直接调用自身编程技巧的方法，其一般会层层转化复杂的大型问题，使其变成小型问题，然后再求解问题[3]。

在一些情况下，递归法能够简化算法，比如求最大公约数的算法。递归法求最大公约数可描述为“自己调用自己”，其离散性的表现有下列两种：一种与求最大值的算法类似；另一种则是指程序运行的离散性，即计算机在栈中实现程序的运行，而栈具有“后进先出”的特点。

该种递归算法在运行中，通过返回“自己”可获得相应的返回值，直至返回获得确定值后，再逐层返回。综上，在递归算法中，计算机每完成一次递归计算，便向内存Push一次，直至计算结束，然后再逐一Pop出。对此，其体现出了计算的离散性，而不是连续性思维模式[4]。

1.3 算法设计的原则

为了保证计算机的运行处理效果，要求算法设计遵循下列几点原则：首先，算法的正确性，算法必须正确无误，要求按需选择科学的算法编写程序，注意算法的结果应具有唯一性；其次，算法的可读性，即保证程序的运算更快、更好；再次，算法的稳定性，即避免计算机的输出曲线出现波动异常；最后，算法的高效低耗性能，即在“节能环保”理念的指导下，实现计算机运行的快速性、低噪声和低能耗。

2 数据结构的离散性

数据结构是对数据元素与数据元素的结构关系进行研究。数据结构一般按元素关系的特性分为网状、树形、线性和集合四种基本结构（见图1），表明数据结构中的数据元素具有离散性[5]。

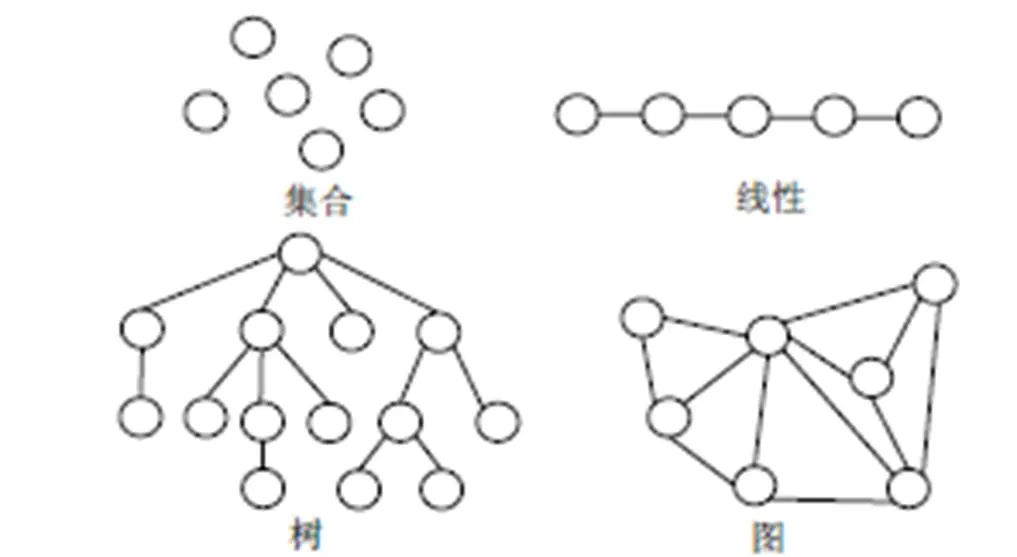
图1 数据结构基本类型

从图1可知，集合结构是由一些离散的数据元素组成的；线性结构具有非常明显的离散性；树形、图形结构均由一些独立存在的数据元素组成，表明数据元素与数据元素的关系具有离散性和不连续性。离散数学是一种未涉及连续变化量的数学，主要用于研究以离散空间为基础的数学结构。对于数据结构，离散数学与其存在非常紧密的关系，比如图论，其研究了数据元素与数据元素的复杂关系。

另外，在计算机中，通过应用离散数学的一些理论知识，解决了一些高难度的问题或实现了解决方法的优化，比如Huffman树，其常用来实现压缩解码。

数字电子是与计算机学科交叉的一门学科，其离散性可采用数字信号进行解释。其中，数字信号是一组数值与时间皆为离散的信号，其对应于模拟信号而且是一组数值与时间皆为连续的信号。数学上认为“连续性”意味着该类信号具有微积分意义，说明离散的信号没有意义[6]。

3 计算机中的离散性问题

在计算机中，二进制的运用赋予了计算机处理问题的离散性特征，而且计算机科学中的算法设计与数据结构两者均可以用二进制阐述其离散性特征。据此，对于计算机中的离散性问题，笔者主要从二进制的角度展开论述。

3.1 二进制

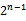
3.2 二进制的离散性

对于音频、视频及图片等信息，人类非常容易理解，但计算机却因只认识“0”和“1”，而无法直接理解该类信息，因此计算机需利用离散的数据认识整个世界。其中，离散的数据可从本质上理解为仅包含“0”和“1”的二进制数据。据此，计算机的处理对象皆为离散的数据。例如，在处理音频时，只有先对连续改变的声音进行二进制处理，才能实现计算机对该类数据的处理。计算机离散化处理音频信息的方法如图2所示。

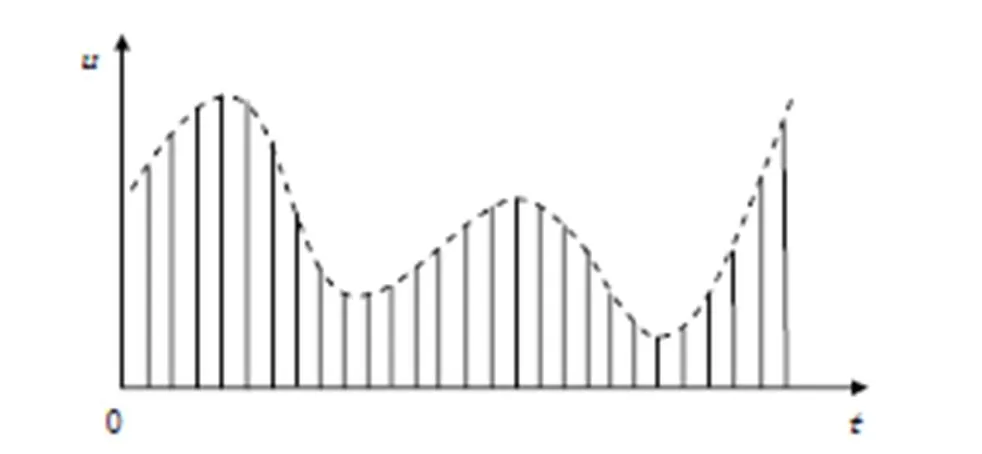
图2 计算机离散化处理音频信息

如图2所示，计算机对音频信息的离散化处理越“细”，则声音更能还原其原貌。

总之，在计算机中，计算机处理问题因二进制的运用而表现出离散性特征，且前文谈及的算法设计、数据结构皆可利用二进制来进行离散性解释。

4 结语

自人类进入21世纪以来，计算机科学实现了飞速发展，且其实际需求量与日俱增，从而激发了相关领域对计算机离散性的重视。在本文，笔者主要探讨了如何利用离散数学来解决计算机的离散性问题。首先，介绍了计算机科学中算法设计的常用方法，即递推法和递归法，并举例探讨了两种方法的离散性体现；其次，介绍了计算机科学中的数据结构与其离散性体现；最后，提出了计算机离散性问题以二进制的运用最为关键。

总之，为了适应计算机科学深入发展的需要，要求深化对计算机科学中算法设计与数据结构的离散性问题的研究。

[1]孔娟华，郑江滨. 一种三维离散点数据生成非结构四面体算法[J]. 计算机工程与科学，2009（1）：35-37.

[2]向裕良，彭佳红. 关于计算机科学中数据结构算法探究[J]. 计算机光盘软件与应用，2013（19）：154-155.

[3]朱雅莉，李肯立. DNA计算机中堆栈数据结构的设计[J]. 计算机工程与科学，2008（4）：121-123，127.

[4]张海燕，张立毅，孙云山. 基于离散剪切波正则化的低剂量CT图像统计重建算法[J]. 计算机工程与科学，2018（1）：86-92.

[5]肖文磊，刘亚醉，Oleksandr Zavalnyi，等.T-SPLINE开源内核的三层数据结构及算法原理[J]. 计算机辅助设计与图形学学报，2017（11）：2023-2036.

[6]赵景昌，高菲，刘光伟，等. 基于散列函数与半边数据结构的TIN拓扑重构算法[J]. 计算机应用研究，2017（12）：3689-3692，3700.

Algorithm Design and Discrete Analysis of Data Structure in Computer Science

Gao Ta

College of Information Science and Technology, Hebei Agricultural University, Hebei Baoding 071000

The paper mainly discusses the discreteness of algorithm design and data structure in computer science. It is used to interpret the abstract solution of computer problems and establish a “continuity→discreteness” thinking mode.

computer science; algorithm design; data structure; discreteness; binary

TP301.6；TP311.1

A