小学数学应用题解题思路分析

徐美贤

摘要：应用题是数学中的重点和难点，特别是一些较复杂的应用题，由于数量关系较隐蔽，题型广博，变化多端以及沿袭传统教学方法和应付考试等原因，学生在解题时很难找出正确的解题思路，会出现这样和那样的问题。如，就题论题，多例一法，对号入座，僵化地套题型套解法等。这有碍于思维训练，不利于智力开发，影响学生分析和解决问题能力的培养。因此，我通过力求多解，数形结合，注意思维创新，讲究技巧几方面介绍，让学生运用已有数学知识，大胆地想象，力求通过不同方法，从不同角度进行探索，培养发散性思维能力，为此应重视各种解题 思路的训练，以拓宽思路，强化思维训练，发展思维能力，提高解题能力。

关键词：审题；思路；思维；语言；创新

一、不拘题型，力求多解

审题是解题的关键，细致深入的审题是顺利解题的必要前提。应用题教学中要防止并纠正审题定题型，解题套方法的定势模式，在达到基本教学要求或学过相关的新知识之后，应当示范并鼓励学生拓宽思路，灵活转移思考角度，优化思维，巧妙解题。

例1.要加工810个零件，单独做甲要15天完工，乙要10天完工。现由甲乙两人合做，需几天完成任务？

分析：按常规解法，由于题目给出了总的工作量，甲、乙分别的工作时间，可以先分别求出甲、乙的工作效率，即甲、乙分别每天加工的零件数，再求出甲乙合做时每天加工的零件数。

解：根据题意，列式计算为

810÷15=54（个）810÷10=81（个）

810÷（54+81）=6（天）

答：甲乙合做完成任务需6天。

注：在学过工程问题后，可启发学生用工程问题的解答思路解答：设要加工的零件总数为“1”，可求出甲、乙的工作效率分别1/15和1/10，列式计算为：

1÷（1/15+1/10）=6（天）………甲乙合做完成任务需6天。

平时训练有素的学生还会这样想：根据题意，这批零件甲用15天做完，乙用10天做完，这就是说，乙做1天相当于甲做1.5天。因此甲乙合做1天，相当于甲单独做（1+1.5）天。甲单独做15天完成的工作，由甲乙合做时，只要15÷（1+1.5）=6（天）

摆脱题型束缚，思路广阔，解法灵活简捷，思维优化会得到充分体现。

二、语言表达，数形结合

语言是思维的工具，也是思维的载体和结果，从想到说，这是理解过程的一个飞跃。所以我们在教学数学应用题时，可以利用教具、图表直观演示，训练学生运用数学语言叙述题目中的已知条件和问题，认识了各个已知条件后，再利用数形结合画出图形，更直观了然，思路更清晰。

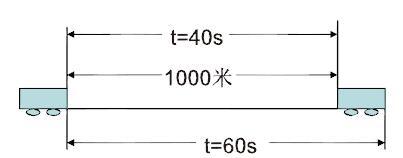
例2、已知一铁路桥长1000米，现有一列火车从桥上通过，测得火车从开始上桥到车身过完桥共用1分钟，整列火车完全在桥上的时间为40秒，求火车的速度及火车的长度？

分析：先画图

求：V车=？L车=？

通过画图，把题目的已知条件和问题都体现出来，问“从图中可以获得什么信息？”（桥长1000米以及走完1000米所用的时间），问“那么用我们所学过的知识可以求出什么量？”（利用路程公式已知S=1000米，t=40s，可以求出：V车），学生经过思考很容易找到各个量之间的关系，然后再根据关系列式计算。进一步已知V车，t=60s，可以得到S1=1000米+ L车，从而得到L车

解：根据题意，可得

V车 =S/t=1000/40=25米/S

S1 = V车×t=25×60=1500米

L车=1500-1000=500米

答：火车的速度为25米/S，火车的长度为500米。

通过画图，数形结合，让学生看图口头叙述解题思路，口头叙述数量关系式，这样既培养了学生的思维能力和语言表达能力，又提高了解题能力，发展了思维的灵活性。

三、不囿常规 思维创新

思维的创新属于思维的高级形式。这种思维不循常规，不拘常法，开拓创新。“可逆性思维是智力发展的重要标志，也是创造能力发展的基矗”可是学生对顺向思维比较敏捷，而对逆向思维则是比较迟钝的，因此，这种思维在当前应用题教学改革中也应力图有所体现。

例3、某蓄水池装有大小两个进水管和一个出水管。如单开大进水管，6小时将空池注满；单开小进水管 则8小时注满空池。要是单开出水管，4小时就可将满池水放完（水的压力略而不计）。在同时打开两个进水管和一个出水管时，多少时间可注满空池？

分析：按常规思路求解，由于已知大进水管的效率是1/6，小进水管的效率是1/8，出水管的效率是1/4，這道题多数学生的做法是：

解：1÷（1/6+1/8-1/4）=24（小时）

思维敏捷的学生对数字比较敏感，可以观察到：24是8、6、4的最小公倍数。设想让三个水管连续开24小时，那么大进水管可注满24÷6=4（池水），小进水管可注满24÷8=3（池水），一共7池水；同时出水管又放走24÷4=6（池水），这样正好还剩1满池水，所以进水管、出水管同时打开，24小时可注满水池。

另解：依题目，得：

24÷[（24÷6+24÷8）-24÷4]

=24÷（4+3-6）=24（小时）

答：24时间可注满空池。

这样解答体现了广阔的思路，活跃的思维，丰富合理的现象和刻意求新的创新意识。如果平时注重提倡和培养学生的创新意识，将会有力促进学生思维能力的发展和提高。

四、不专强攻 讲究智取

有些应用题如按原定思路解，会出现此路（包括知识局限）不通或解答过繁等，遇到此情况时，就要引导学生放弃原来想法，思谋它法处理。

例4.有批枕木，每根长1.8米，枕木的两个相对的侧面是面积都等于5平方分米的正方形。现要把它们加工成体积最大的圆木段，求每根圆木的体积？

分析：此题解答过程很不顺利，正确率极低。教师指点，对“加工成体积最大的圆木段”一语，正确理解为，要使圆木底面直径与枕木的侧面正方形边长相等，但求解中不少学生是按着求底面半径→ 底面圆面积→圆柱体积的思路，苦苦地寻求圆半径，却没有结果，使解题断路搁浅。因为他们无法从正方形的面积等于 5平方分米中求出边长，自然也无法求出圆的直径。

强攻失败，吸取教训，采用智取。想圆面积公式S=πr2，如果知道圆的半径，固然可求出圆的面积。可是很少学生想到要是知道了圆的半径的平方，能求得圆的面积吗？“对啊，不是只要在r2前面再乘上π就是圆的面积了吗。”为此，不少学生心头一亮，精神大振。如果把正方形的边长就记作2r，那么，从边长×边长=5平方分米，就可得2r×2r=5平方分米，即 4r2=5平方分米，所以r2=5/4平方分米，进而可求出圆木底面积：π×5/4= 5/4π，这时再求圆木体积已不难：

解：记正方形的边长就作2r

2r×2r=5（平方分米）

4r2=5（平方分米），即r2=5/4平方分米，

V圆木=πr2×h=π×5/4×18=70.65（立方分米）

答：每根圆木的体积为70.56立方分米。

在深受困惑和付出辛劳之后的成功分外令人愉悦。这样美妙而全新的思路在教学中相机运用，对促进学生的思维发展和能力提高无疑是极为有益的。

总之，应用题解题分为情节过程和数学过程两个部分，是一个严谨的思维活动过程，要求学生具有塌实的知识基础和良好的思维品质，需要学生点滴积累从实践中获取经验，达到质的飞跃。在解题时，要仔细审题，理清条件与问题，数形结合，力求多解，注意思维创新，讲究技巧，以致解题能力不断提高。

参考文献：

[1]李济元 新课标题库 陕西人民教育出版社2006.8

[2]许芬英等主编 新课标教案 人民教育出版社2006.6