基于贪婪选择的半朴素贝叶斯分类器研究

王 辉，张 帆，李玉杰

(中央民族大学信息工程学院，北京 100081)

0 引言

数据挖掘的深入发展，赋予数据新的意义，通过数据的不断积累和挖掘，可以从数据中获得更多有价值和有意义的信息，因此数据挖掘(Data mining，DM)[1]的重要性尤其突出.朴素贝叶斯分类器(Naive Bayes Classifiers，NBC)[2]作为经典的数据挖掘算法，在科研领域快速发展，但NBC假设属性间条件独立，忽略它们之间应用的联系.

对NBC的改进相对比较发散，不同应用场景下对NBC的改进方式也是千差万别的，但归结起来，主要有以下几种思路：(1)基于贝叶斯网络结构扩展技术放宽属性独立性假设方面的改进，典型代表为树依赖扩展的著名TAN分类器[3]；(2)基于属性选择技术，改进模型分类方法，此种方法可以借助聚类、互信息[4]、属性贪婪搜索算法等对属性空间进行子集化分，剔除无关噪声属性，对属性进行分组保留，这类分类器称为选择性贝叶斯分类器[5](Selective Bayesian Classifier，SBC)；(3)基于概率调整技术改进NBC的算法，如采用了充分加权算子作为概率乘积的权重来扩展NBC[6]；(4)王双成等[7]基于TAN分类器进行无向网络依赖扩展，把属性之间的树结构扩展成可分解马尔科夫网络，使经过依赖扩展得到的分类器能够更有效地利用属性间的依赖信息，提高分类能力，并能够通过调节阈值大小避免过度拟合.

各种对NBC独立性假设方面的改进，在不同数据集上不同程度地提高了数据分类准确性，说明从独立性假设方面改进NBC是有效可行的.

本文将贪婪选择算法思想运用于半朴素贝叶斯分类器的属性分组，通过对属性的循环扫描获取到最优属性分组，直至所有属性划分结束，获得最终分组结果，最后利用所获取的分组进行分类预测，较好地改进了朴素贝叶斯分类器的不足.

1 半朴素贝叶斯分类器

半朴素贝叶斯分类器[8](Semi-Naive Bayesian Classifier，SNBC)是通过寻找并利用NBC的属性依赖关系进行依赖扩展的分类器.用πi作为变量集合X的一个划分(组的划分方法将在下文中给出介绍)，假设待分类数据各组之间条件相互独立，组内数据各属性相互依赖，通过合理选取依赖性强的几个属性作为属性组来达到改进分类器的目的，依赖性强弱模型可以表示为

(1)

推知SNBC模型为

(2)

通过(2)式可知分母的值对于选定的数据集是一个定值，使用中以常数对待，重点解决求解分子问题，取其最大值表示属性组π属于类C的可能性.SNBC表示为

(3)

2 模型建立与评价体系

本文将贪婪选择算法思想融入到朴素贝叶斯分类器的改进过程中，结合分类器判别标准进行相应的实验.

2.1 贪婪选择算法

贪婪选择算法(Greedy Selection Algorithm，GSA)又称为贪心算法[9]，在寻找最优解或最佳路径问题中有着广泛的应用.实际应用中将待求解问题分拆成多个步骤进行，分步求得局部最优解，以最优解为所需结果.在求解过程中，通过一次次的局部最优解的求解，获得一系列局部最优选择，从而找出所求问题的全局最优解.

2.2 数据来源及模型建立

(1) 数据来源.实验所用数据来自国际标准数据集仓库UCI，选取21个数据集用于实验，进行贝叶斯分类的学习.

(2) 模型建立.分组模型采用贪婪选择算法顺序求解，按照寻求最优的原则进行，在实验过程中通过相关参数的调整，获取最优的分类效果，实验步骤如下：

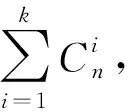
步骤2：利用3种判别标准(概率最大原则、属性出现次数最少原则、属性出现次数最少原则基础上的概率最大化原则)，分别获取最佳属性分组.

步骤3：重新组合数据，获取分类结果.

步骤4：利用步骤1获取到的结果，重复步骤2、步骤3，设定不同的权值和参数，获取最佳分类效果.

步骤5：利用实验所选取的数据集，与主流分类器做对比实验.

2.3 评价标准

本文以分类器的分类准确率作为判断分类器性能的标准，准确率是目录最为常用的分类器判断标准，特点是计算简单，能体现出分类器的实际分类效果.计算公式为

在分类器分类性能验证过程中，采用国际通用的十折交叉验证(10-fold cross-validation)方法[9]，即在实验过程中，将每一个数据集D均分为10份(D1，D2，…，D10)，对每一份实验数据单独训练分类模型，对训练好的模型应用于其他兄弟集进行分类准确性验证，保证了在小数据集情况下也可以得到很好的分类效果.十折交叉法表达式为

(4)

为了获得更好的测试效果，D1，D2，…，D10利用随机算法随机产生，保证分类器选用训练集的普适性.当k=|D|时，使用leave-one-out法(每次测试仅用一个测试数据，其他数据用于训练)进行估计，对不同分类器分类准确性进行比较.本文采用Everitt提出的比较方法McNemar测试[10]，该方法要求把数据集D分成训练集Dh和测试集Dt2个部分，在训练集上利用不同的学习算法A和B，得到对应的分类器FA和FB，之后通过测试集对训练出的分类器进行测试，并构造出列联表(见表1).

表1 列联表

表中分类数据总和为n00+n01+n10+n11.

3 实验与分析

利用贪婪搜索算法构建分类模型，进行反复对比实验并调整参数，获得最佳实验结果.在实验过程中，采用朴素贝叶斯(NB)分类器、朴素贝叶斯的链扩展(CENB)分类器、朴素贝叶斯的树扩展(TENB)分类器、朴素贝叶斯的图扩展(GENB)分类器、C4.5分类器(C4.5)、分类与回归树(CARET)分类器和BP神经网络(BPNN)分类器、贪婪选择算法改进的NBC(GSA-NB)进行分类实验[11]，其中GSA-NB1、 GSA-NB2 、GSA-NB3代表3种分组原则获取的分类准确率(见表2).

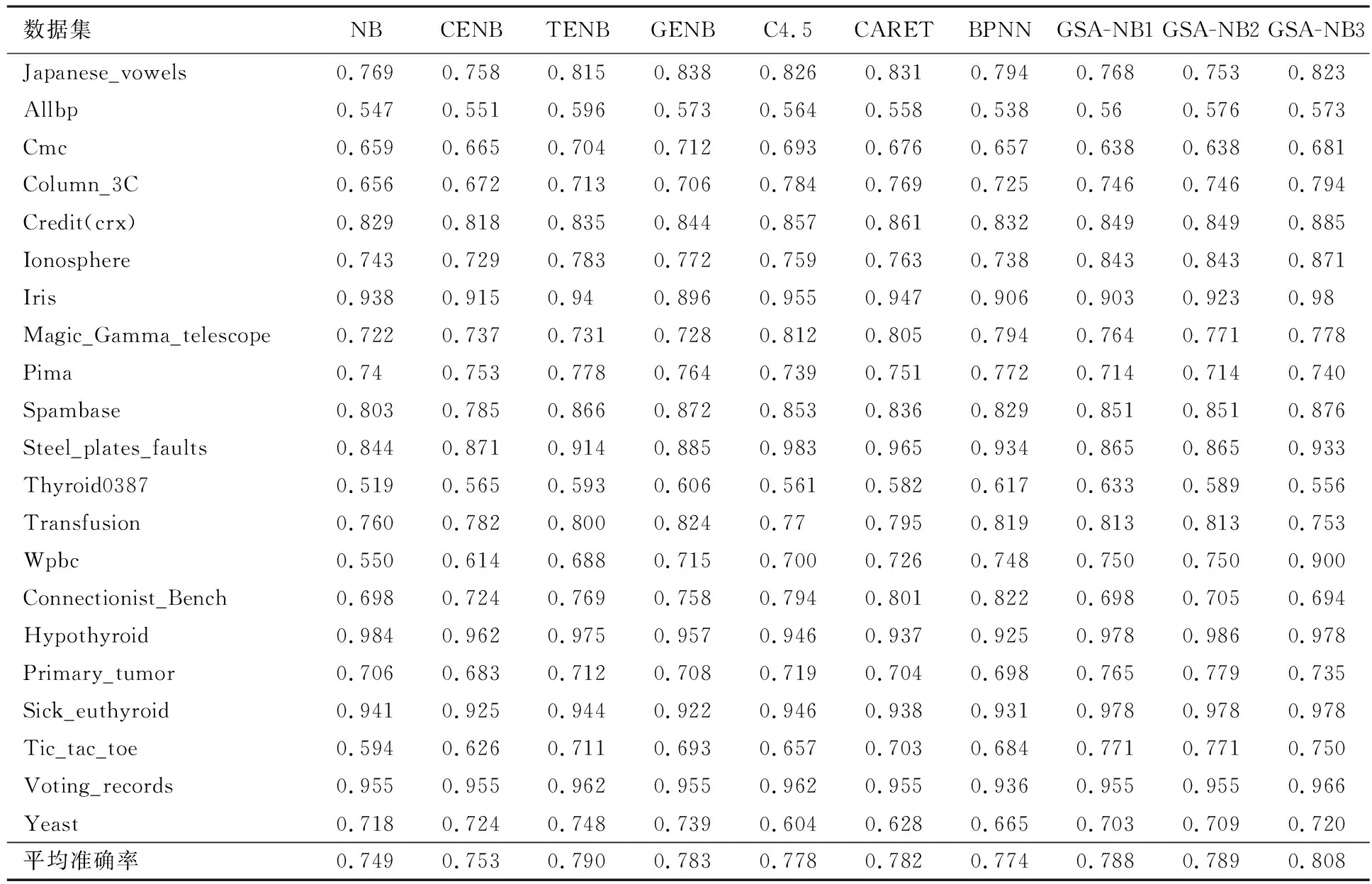
表2 实验结果与其他分类器分类结果对比

由表2可知：对不同的数据集，改进方式体现出了差异性.3种分类原则在数据集上平均分类效果优于对比分类器，大部分数据集分类准确率有了不同程度的提升，个别数据集改进效果不明显.

GSA-NB3与其他分类器在21个数据集上进行了对比，分类准确率的散点对比情况见图1.图1中的点代表对应分类器的准确率，对角线上方的点代表在相同数据集下的纵坐标对应分类器的分类准确率高于横坐标分类器，反之则代表小于横坐标分类器.

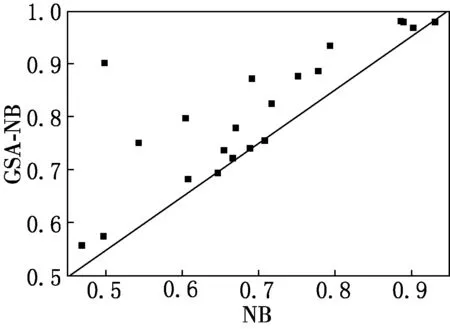
(a)NB与GSA-NB

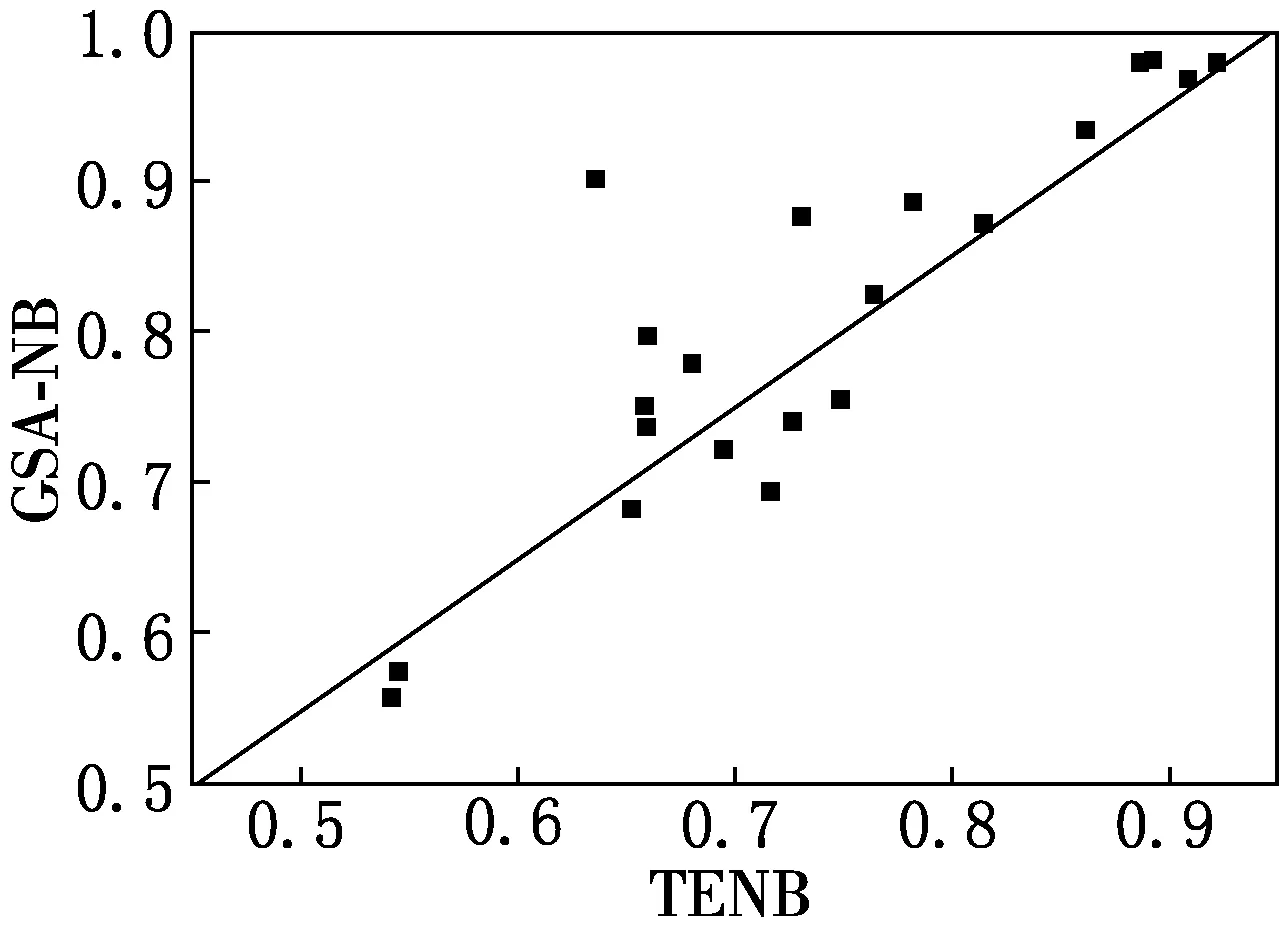
(c)TENB与GSA-NB

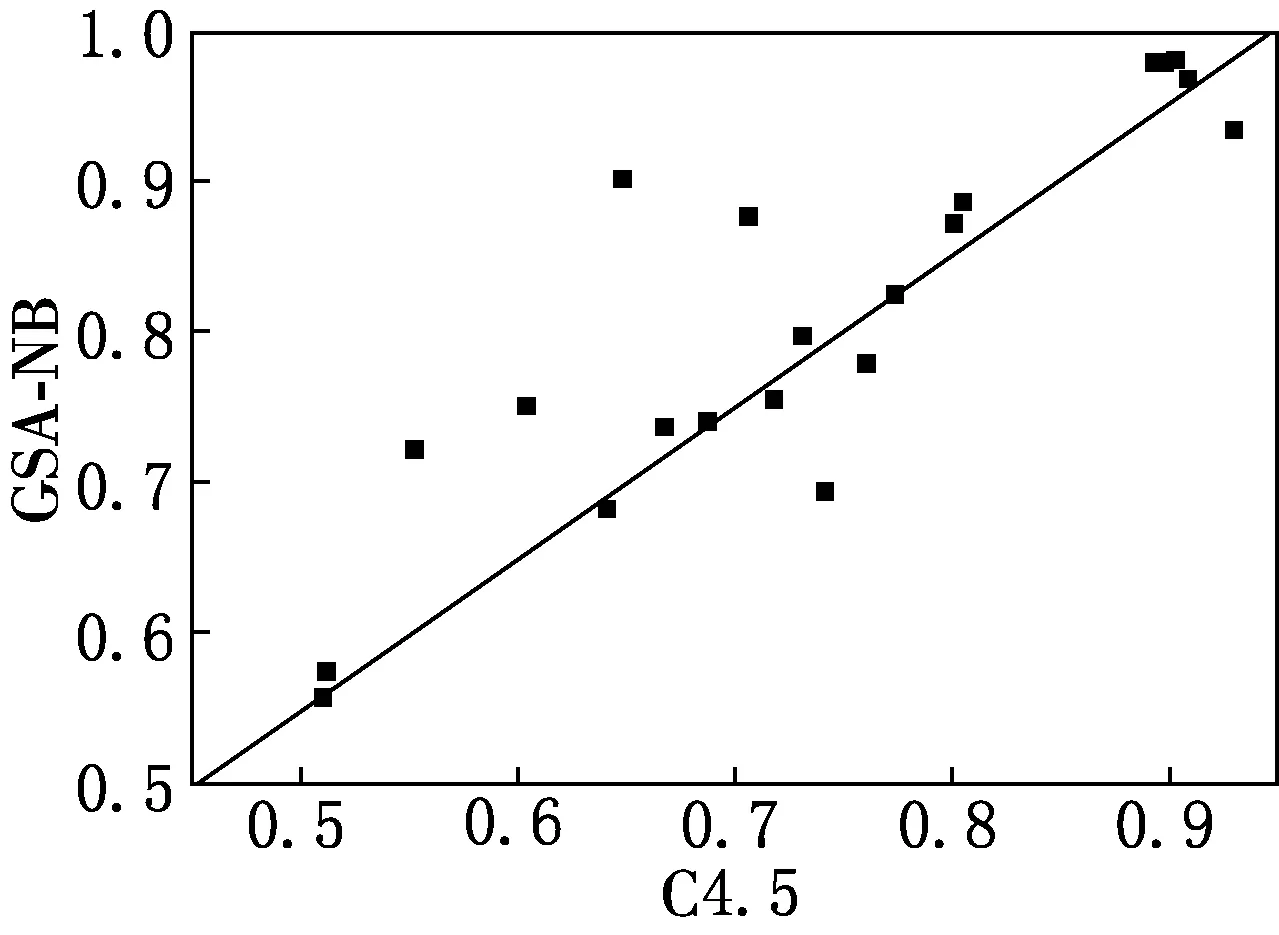
(e)C4.5与GSA-NB

从图1可以看出，GSA-NB3分类准确率除个别数据集略逊于对比分类器外，分类效果有明显提升，在21个数据集中，以GSA-NB3与对比分类器在分类准确率方面做差异统计，以区段([0.5%，∞)、(-0.5%，0.5%)、(-∞，-0.5%])作为对比分类器计数依据获得百分比统计结果如表3所示.

表3 GSA-NB3与其他分类器分类结果对比 %

在所选取的21个相同数据集下各分类器分类准确率的差异统计中，GSA-NB3的平均分类准确率明显优于对比分类器，说明改进的分类器GSA-NB在分类准确率方面优于其他分类器.

4 小结

本文在NBC和SNBC理论基础上，建立了基于贪婪选择算法的GSA-NB分类器.GSA-NB在属性组合方面选用合理的分组规则，在实验过程中进行参数调整，充分利用了属性间的依赖关系.实验过程从UCI数据库中选取21个数据集进行分类和对比实验，分别从理论和实验验证了对NBC进行扩展的必要性和扩展方法的合理有效性.

[参 考 文 献]

[1] 黄春华，陈忠伟，李石君.贝叶斯决策树方法在招生数据挖掘中的应用[J].计算机技术与发展，2016(4)：114-118.

[2] 王辉，王双成，周颜军，等.基于广义朴素贝叶斯分类器的空值处理方法[J].东北师大学报(自然科学版)，2004，36(1)：34-38.

[3] PERNKOPF F，BILMES J A.Efficient heuristics for discrimi-naive structure learning of Bayesian network classifiers[J].Journal of Machine Learning Research，2010，11：2323-2360.

[4] 赵亮，刘建辉，崔彩峰.互信息匹配的半朴素贝叶斯分类器[J].计算机工程与应用，2015(18)：84-87.

[5] 王辉，韩旭，王双成，等.连续属性朴素贝叶斯分类器的依赖扩展研究[J].东北师大学报(自然科学版)，2012，44(2)：41-45.

[6] YAGER-R R.An extension of the Naïve Bayesian classifier[J].Information Science，2006，176：577-588.

[7] 王双成，高瑞，杜瑞杰.具有超文结点时间序列贝叶斯网络集成回归模型[J].计算机学报，2017，40(12)：2748-2761.

[8] JULIA M，FLORES J A，GAMEZ J M，et al.Domains of competence of the semi-naive Bayesian network classifiers[J].Information Sciences，2014，260(1)：120-148.

[9] CHICKERING D M.Learning equivalence classes of Bayesian network structures[J].Journal of Machine Learning Research，2002，2(3)：445-498.

[10] ADEDOKUN OA，BURGESS WD.Analysis of paired dichotomous data：a gentle introduction to the McNemar test in SPSS[J].Journal of Multidisciplinary Evaluation，2012，8(17)：125-131.

[11] 王双成，高瑞，杜瑞杰.基于高斯Copula的约束贝叶斯网络分类器研究[J].计算机学报，2016，39(8)：1612-1625.