关于δ-Jordan李三系的交换扩张

李 强，马丽丽，田 巍

(齐齐哈尔大学理学院，黑龙江 齐齐哈尔 161006)

1 预备知识

李代数的二元运算与李三系的三元运算密切相关.若定义李代数中运算[x，y，z]=[[x，y]，z]，则李代数即为李三系.作为李三系的推广，Okubo和Kamiya[1]介绍了δ-Jordan李三系的概念.当δ=1时，δ-Jordan李三系即为李三系.2002年，他们又运用δ-Jordan李三系构造了一类单Jordan超代数[2].

Yamaguti[3]提出了李三系的表示和上同调理论.2004年，Kubo和Taniguchi[4]给出了上同调在李三系的形变和扩张理论中起到的重要作用.近年来，运用上同调理论讨论了一些代数的结构和表示.[5-9]文献[5]中构造了δ-Jordan李三系的表示和低阶上同调，本文在此基础上，利用δ-Jordan李三系的3-上圈构造δ-Jordan李三系，并且研究交换扩张的等价.若不特殊声明，本文基本符号均与文献[5]中一致.

定义1[1]δ-Jordan李三系(T，[·，·，·]，δ)由域F上向量空间T，一个三元运算[·，·，·]：T×T×T→T构成，并满足∀x，y，z，u，v∈T，下列等式成立：

[x，y，z]=-δ[y，x，z]，

(1)

[x，y，z]+[y，z，x]+[z，x，y]=0，

(2)

[x，y，[z，u，v]]=[[x，y，z]，u，v]+[z，[x，y，u]，v]+δ[z，u，[x，y，v]].

(3)

定义2[5]设(T，[·，·，·]，δ)是δ-Jordan李三系，V是域F上的向量空间.A∈End(V)，(V，θ)称为关于A的T-模，若存在双线性映射θ：T×T→End(V)，(x，y)ax，y)，使得∀x，y，z，u∈T，满足：

θ(z，u)θ(x，y)-δθ(y，u)θ(x，z)-θ(x，[y，z，u])+D(y，z)θ(x，u)=0，

(4)

δθ(z，u)D(x，y)-δD(x，y)θ(z，u)+θ([x，y，z]，u)+δθ(z，[x，y，u])=0，

(5)

δD(z，u)D(x，y)-D(x，y)D(z，u)+δD([x，y，z]，u)+δD(z，[x，y，u])=0，

(6)

其中D(x，y)=θ(y，x)-δθ(x，y).则称θ为(T，[·，·，·]，δ)关于A在V上的表示.当θ=0时，称V为关于A的平凡T-模.

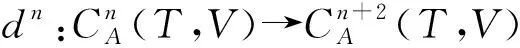
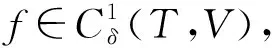
d1f(x1，x2，x3)=(x2，x3)f(x1)-δθ(x1，x3)f(x2)+δD(x1，x2)f(x3)-f([x1，x2，x3])；

d2f(y，x1，x2，x3)=θ(x2，x3)f(y，x1)-δθ(x1，x3)f(y，x2)+
δD(x1，x2)f(y，x3)-f(y，[x1，x2，x3])；

d3f(y1，y2，x1，x2，x3)=θ(x2，x3)f(y1，y2，x1)-δθ(x1，x3)f(y1，y2，x2)-

δD(y1，y2)f(x1，x2，x3)+D(x1，x2)f(y1，y2，x3)+
f([y1，y2，x1]，x2，x3)+f(x1，[y1，y2，x2]，x3)+
δf(x1，x2，[y1，y2，x3])-f(y1，y2，[x1，x2，x3]).

2 主要结果

为了方便，把3-上圈的概念改写为：

定义4设(T，[·，·，·]，δ)是δ-Jordan李三系，(V，θ)为T-模，则线性映射ω：⊗3→V称为3-上圈，如果其满足：

ω(x1，x2，x3)=-δω(x2，x1，x3)，
ω(x1，x2，x3)+ω(x2，x3，x1)+ω(x3，x1，x2)=0，
ω(x1，x2，[y1，y2，y3])+δD(x1，x2)ω(y1，y2，y3)=
ω([x1，x2，y1]，y2，y3)+ω(y1，[x1，x2，y2]，y3)+δω(y1，y2，[x1，x2，y3])+
θ(y2，y3)ω(x1，x2，y1)-δθ(y1，y3)ω(x1，x2，y2)+D(y1，y2)ω(x1，x2，y3).

δ-Jordan李三系T的理想是子空间I，使得[I，T，T]⊆I.理想I称为交换理想，若满足[T，I，I]=0.由于[T，I，I]=0，易知[I，T，I]=0和[I，I，T]=0成立.

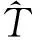
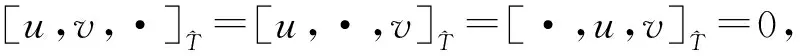
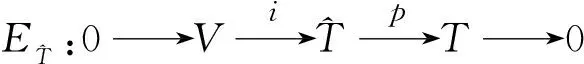
定理1设θ是δ-Jordan李三系(T，[·，·，·]，δ)关于A在V上的表示，ω为3-上圈，定义运算如下：

[x1+u1，x2+u2，x3+u3]ω=
[x1，x2，x3]+ω(x1，x2，x3)+δD(x1，x2)(u3)-δθ(x1，x3)(u2)+θ(x2，x3)(u1)，

这里x1，x2，x3∈T，u1，u2，u3∈V.则T⨁V关于定义的运算构成δ-Jordan李三系.

证明首先证明(1)式成立.

[x1+u1，x2+u2，x3+u3]ω=
[x1，x2，x3]+ω(x1，x2，x3)+δD(x1，x2)(u3)-δθ(x1，x3)(u2)+θ(x2，x3)(u1)=
-δ([x2，x1，x3]+ω(x2，x1，x3)+δD(x2，x1)(u3)+θ(x1，x3)(u2)-δθ(x2，x3)(u1))=
-δ[x2+u2，x1+u1，x3+u3]ω.

其次，由于ω是3-上圈，且D(x，y)=θ(y，x)-δθ(x，y)，可得

[x1+u1，x2+u2，x3+u3]ω+[x2+u2，x3+u3，x1+u1]ω+[x3+u3，x1+u1，x2+u2]ω=
[x1，x2，x3]+ω(x1，x2，x3)+δD(x1，x2)(u3)-δθ(x1，x3)(u2)+θ(x2，x3)(u1)+
[x2，x3，x1]+ω(x2，x3，x1)+δD(x2，x3)(u1)-δθ(x2，x1)(u3)+θ(x3，x1)(u2)+
[x3，x1，x2]+ω(x3，x1，x2)+δD(x3，x1)(u2)-δθ(x3，x2)(u1)+θ(x1，x2)(u3)=0.

表明(2)式成立.

下面只需证明(3)式成立即可.

[x1+u1，x2+u2，[y1+v1，y2+v2，y3+v3]ω]ω=
[x1+u1，x2+u2，[y1，y2，y3]+ω(y1，y2，y3)+δD(y1，y2)(v3)-
δθ(y1，y3)(v2)+θ(y2，y3)(v1)]=
[x1，x2，[y1，y2，y3]]+ω(x1，x2，[y1，y2，y3])-δθ(x1，[y1，y2，y3])(u2)+
θ(x2，[y1，y2，y3])(u1)+δD(x1，x2)(ω(y1，y2，y3)+δD(y1，y2)(v3)-
δθ(y1，y3)(v2)+θ(y2，y3)(v1))，

[[x1+u1，x2+u2，y1+v1]ω，y2+v2，y3+v3]ω=
[[x1，x2，y1]+ω(x1，x2，y1)+δD(x1，x2)(v1)-
δθ(x1，y1)(u2)+θ(x2，y1)(u1)，y2+v2，y3+v3]ω=
[[x1，x2，y1]，y2，y3]+ω([x1，x2，y1]，y2，y3)+
δD([x1，x2，y1]，y2)(v3)-δθ([x1，x2，y1]，y3)(v2)+
θ(y2，y3)(ω(x1，x2，y1)+δD(x1，x2)(v1)-
δθ(x1，y1)(u2)+θ(x2，y1)(u1))，

[y1+v1，[x1+u1，x2+u2，y2+v2]ω，y3+v3]ω=
[y1+v1，[x1，x2，y2]+ω(x1，x2，y2)+δD(x1，x2)(v2)-
δθ(x1，y2)(u2)+θ(x2，y2)(u1)，y3+v3]ω=[y1，[x1，x2，y2]，y3]+
ω(y1，[x1，x2，y2]，y3)+δD(y1，[x1，x2，y2])(v3)+
θ([x1，x2，y2]，y3)(v1)-δθ(y1，y3)(ω(x1，x2，y2)+δD(x1，x2)(v2)-
δθ(x1，y2)(u2)+θ(x2，y2)(u1))，

δ[y1+v1，y2+v2，[x1+u1，x2+u2，y3+y3]ω]ω=
δ([y1+v1，y2+v2，[x1，x2，y3]+ω(x1，x2，y3)+δD(x1，x2)(v3)-
δθ(x1，y3)(u2)+θ(x2，y3)(u1)]ω)=δ([y1，y2，[x1，x2，y3]]+
ω([y1，y2，[x1，x2，y3]])-δθ(y1，[x1，x2，y3])(v2)+
θ(y2，[x1，x2，y3])(v1)+δD(y1，y2)(ω(x1，x2，y3)+δD(x1，x2)(v3)-
δθ(x1，y3)(u2)+θ(x2，y3)(u1))).

由(4)—(6)式与ω为3-上圈可得

[x1+u1，x2+u2，[y1+v1，y2+v2，y3+v3]ω]ω=[[x1+u1，x2+u2，y1+v1]ω，y2+v2，y3+v3]ω+
[y1+v1，[x1+u1，x2+u2，y2+v2]ω，y3+v3]ω+δ[y1+v1，y2+v2，[x1+u1，x2+u2，y3+v3]ω]ω.

于是T⨁V关于定理定义的运算是δ-Jordan李三系.

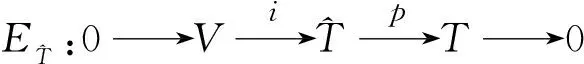
证明必要性.令F：T⨁ωV→T⨁ω′V为同态，则有

F[x1，x2，x3]ω=[F(x1)，F(x2)，F(x3)]ω′.

(7)

由已知两个交换扩张等价，则存在ρ：T→V使得

F(xi+ui)=xi+ρ(xi)+ui，i=1，2，3.

(8)

(7)式左端为

F([x1，x2，x3]+ω(x1，x2，x3))=[x1，x2，x3]+ω(x1，x2，x3)+ρ([x1，x2，x3])，

(7)式右端为

[x1+ρ(x1)，x2+ρ(x2)，x3+ρ(x3)]ω′=
[x1，x2，x3]+ω′(x1，x2，x3)+δD(x1，x2)ρ(x3)-δθ(x1，x3)ρ(x2)+θ(x2，x3)ρ(x1).

比较等式(7)的两端，可知

(ω-ω′)(x1，x2，x3)=
δD(x1，x2)ρ(x3)-δθ(x1，x3)ρ(x2)+θ(x2，x3)ρ(x1)-ρ([x1，x2，x3]).

于是ω-ω′=d1ρ，即ω与ω′属于相同的同调类.

充分性.若ω与ω′属于相同的同调类，则可设ω-ω′=d1ρ，再如(8)式定义F，类似必要性的证明可得结论.

[参 考 文 献]

[1] OKUBO S，KAMIYA N.Jordan-Lie superalgebra and Jordan-Lie triple system[J].J Algebra，1997，198(2)：388-411.

[2] KAMIYA N，OKUBO S.A construction of simple Jordan superalgebra ofFtype from a Jordan-Lie triple system[J].Ann Mat Pura Appl，2002，181(3)：339-348.

[3] YAMAGUTI K.On the cohomology space of Lie triple system[J].Kumamoto J Sci Ser A，1960，5：44-52.

[4] KUBO F，TANIGUCHI Y.A controlling cohomology of the deformation theory of Lie triple systems[J].J Algebra，2004，278(1)：242-250.

[5] MA L L，CHEN L Y.Onδ-Jordan Lie triple systems[J].Linear Multilinear Algebra，2017，65(4)：731-751.

[6] LIN J，CHEN L Y，MA Y.On the deformation of Lie-Yamaguti algebras[J].Acta Math Sin，2015，31(6)：938-946.

[7] LIN J，WANG Y，DENG S Q.T*-extension of Lie triple systems[J].Linear Algebra Appl，2009，431(11)：2071-2083.

[8] ZHAO J，CHEN L Y，MA L L.Representations andT*-extensions of hom-Jordan-Lie algebras[J].Comm Algebra，2016，44(7)：2786-2812.

[9] ZHANG T.Notes on cohomologies of Lie triple systems[J].J Lie Theory，2014，24(4)：909-929.