中低速磁浮列车不同工况下的牵引仿真计算
陈祎格
(北京磁浮交通发展有限公司,100124,北京//工程师)
磁浮列车牵引计算不同于其他城市轨道交通车辆及干线电力机车的牵引计算。由于列车与地面轨道间无机械接触,并且采用了直线电机电磁力驱动方式,故其线路适应性强、转弯半径小(最小转弯半径可达50 m)、爬坡能力强(最大坡度可达70‰)。
此外,城市轨道交通一般运行区间较短,运行中要频繁转换于牵引工况及制动工况之间。这对列车运行的平稳性及舒适性提出了更高的要求,牵引仿真计算可为运营管理提供参考。
1 磁浮列车受力分析
1.1 列车运行动态分析
根据受力分析,磁浮列车的合力为
C=ma=F-B-W
(1)
式中:
C——列车所受的合力;
m——列车的总质量;
a——列车的加速度;
F——列车所受的牵引力;
W——列车所受的阻力;
B——列车所受的制动力。
故,当列车处于牵引工况时,B=0,C=F-W;当列车处于惰行工况时,F=0,B=0,C=-W;当列车处于制动工况时,F=0,C=-W-B。
设计算步长时间为t0,则列车在第n+1个t0后完成的运行距离S0(n+1)及运行速度v0(n+1)为:
v0(n+1)=v0(n)+at0
(2)
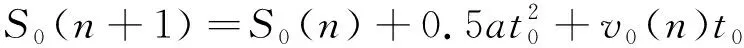
(3)
由于线路情况不同,且运行工况不断变化,故加速度a也不断变化。如t0足够小,则在每个t0内作用在列车上的合力近似为1个常数,a也可视为不变,即视列车作匀变速运动。
1.2 运行阻力分析
列车总阻力为基本阻力与附加阻力之和。
1.2.1 基本阻力
当磁浮列车运行时,其车体与轨道间无机械接触,故其基本阻力的组成与轮轨列车有所不同。磁浮列车的基本阻力包括空气阻力、电磁阻力和受流器阻力[1]。
根据经验公式,有:
式中:
Wm——列车所受的电磁阻力,N;
m——列车质量,t;
v——列车速度,m/s。
且有:
Wc=41.67N
式中:
Wc——列车所受的受流器阻力,N;
N——列车编组数。
空气动力学阻力Wa与阻力系数、空气密度、相对速度的平方及列车最大截面积成正比。采用日本磁浮列车HSST-100L的经验公式,有:
Wa=(1.652+0.572N)v2
(4)
式中:
Wa——空气动力学阻力,N。
1.2.2 附加阻力
磁浮列车的附加阻力主要与线路参数有关[2]。附加阻力包括坡道阻力、曲线阻力及隧道阻力。其中,隧道阻力与前两个阻力相比要小很多,故计算中可忽略不计。
坡道阻力公式为:
Wi=mgi
(5)
式中:
Wi——列车所受坡道阻力,N;
g——重力加速度,m/s2;
i——坡道坡度,‰。
曲线阻力的经验公式为:
Wr=mg600/R
(6)
式中:
Wr——列车所受曲线阻力,N;
R——曲线半径,m。
1.3 牵引力与制动力
磁浮列车采用6辆编组全动车直线电机牵引方式,由直线电机产生的电磁力驱动。直线电机的牵引力不仅与列车运行速度、载荷工况,以及电机供电电压、电流有关,还与电机的气隙高度有关[3]。
在牵引仿真计算中,牵引力是根据电机牵引特性曲线(见图1)来确定的,可采用Matlab软件以曲线拟合的方法得到牵引力与速度的函数关系,从而确定不同速度对应的牵引力[4]。
磁浮列车制动有电制动、电空混合制动和纯空气制动等方式。空气制动系统具有常用制动、快速制动及紧急制动功能。常用制动与快速制动采用电空混合制动方式,并以电制动方式优先;电制动不能满足要求时,以空气制动作为补充。紧急制动为纯空气制动,产生最大的制动力和制动减速度。快速制动采用和紧急制动相同的制动减速度。图2为空气制动与电制动的制动力变化图。

图1 牵引特性曲线
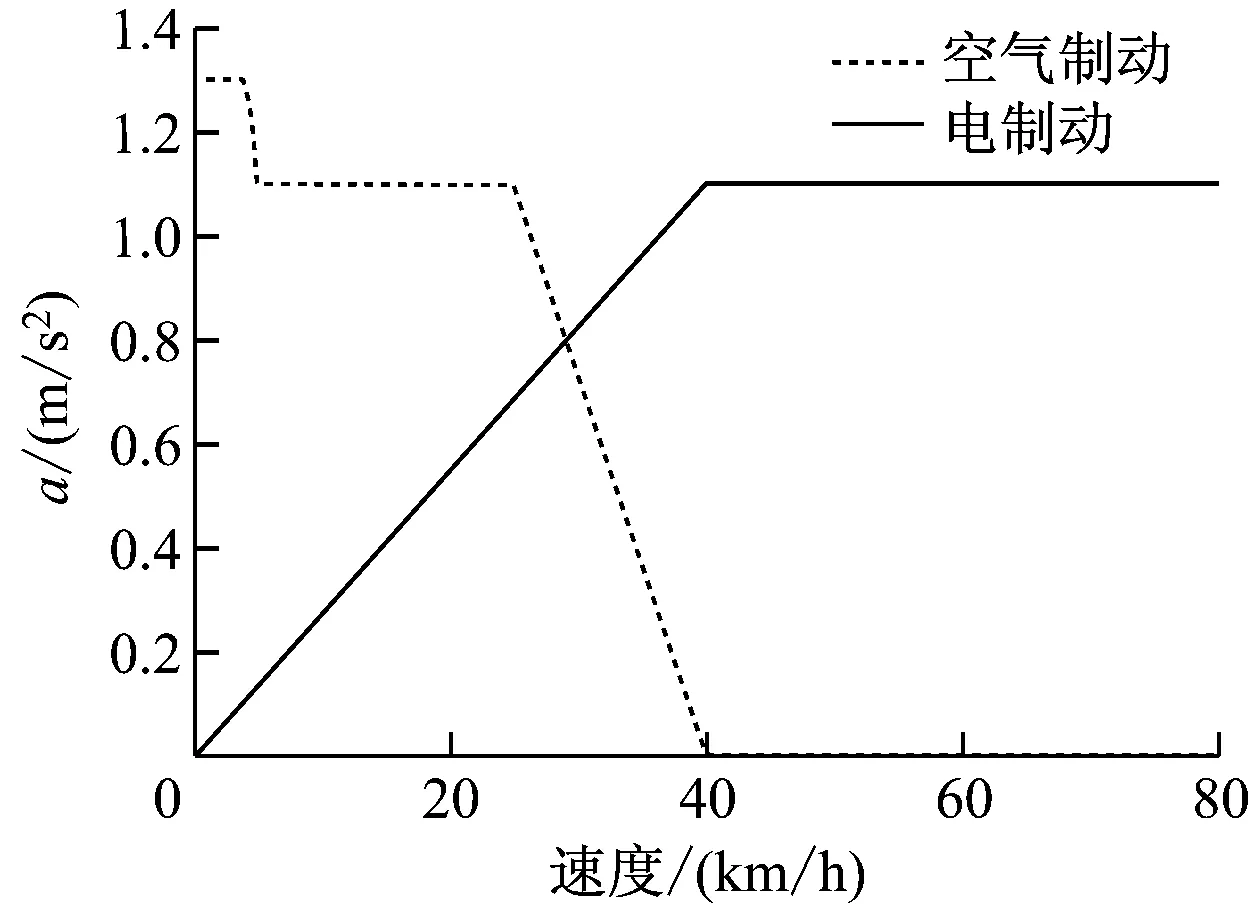
图2 制动力变化图
制动工况仿真可实时计算出列车所需总制动力,及当前速度下的列车电制动力。当电制动力不足时,每辆动车按平均分配原则同时施加空气制动力。在实际情况中,只要电制动正常,除列车低速运行工况外,一般不需要补充空气制动。
2 牵引计算策略
列车的运行工况有牵引、惰行及制动3种。牵引仿真计算的控制策略即对不同工况进行选择。当列车进入1个新区段时,可根据坡道、曲线等线路信息获得前方路段限速信息,及早调整运行工况,以避免发生紧急制动情况,避免牵引工况与制动工况的直接转化,从而提高乘客乘车的舒适性。选择列车运行工况可遵循以下原则:
(1) 牵引工况:当列车起动时,当列车运行速度小于设定的本区段最低运行速度时,以及列车运行至上坡路段时,均应选择牵引工况。
(2) 惰行工况:当列车在牵引工况下,如在平直路段运行速度达到该路段最大限速值,则应选择惰行工况。列车即将进入下坡段时,也应选择惰行工况。
(3) 制动工况:列车运行在下坡路段时,如运行速度达到本路段最大限速,则应选择制动工况。当列车即将进站或遇紧急情况需要停车时,当列车当前运行速度大于即将进入的前方区段最大限速时,均应选择制动工况。
列车切换至制动工况前,应先确定其制动的起点。以列车至限速路段或区间终点的距离s及v为主要变量,以列车制动起点至限速路段或区间终点的距离s0、限制的速度v0作为计算的初值,根据制动力计算出列车加速度(a>0),即可得到反向制动v-s(速度-距离)曲线[5]。以反向制动v-s曲线与当前列车运行v-s曲线的交点作为列车运行转为制动工况的起点,以反向制动v-s曲线与本区段最高限速线的交点作为制动反算点[6]。
除了考虑上述原则外,为提高运行效率、减少能耗,在各区段还设置了最低运行速度(比该区间最大限速值小10 km/h)作为各工况之间转换的条件,使列车运行速度始终在此范围内波动。
根据上述原则,得到了牵引、惰行及制动工况下的控制算法。控制流程图如图3~6所示。
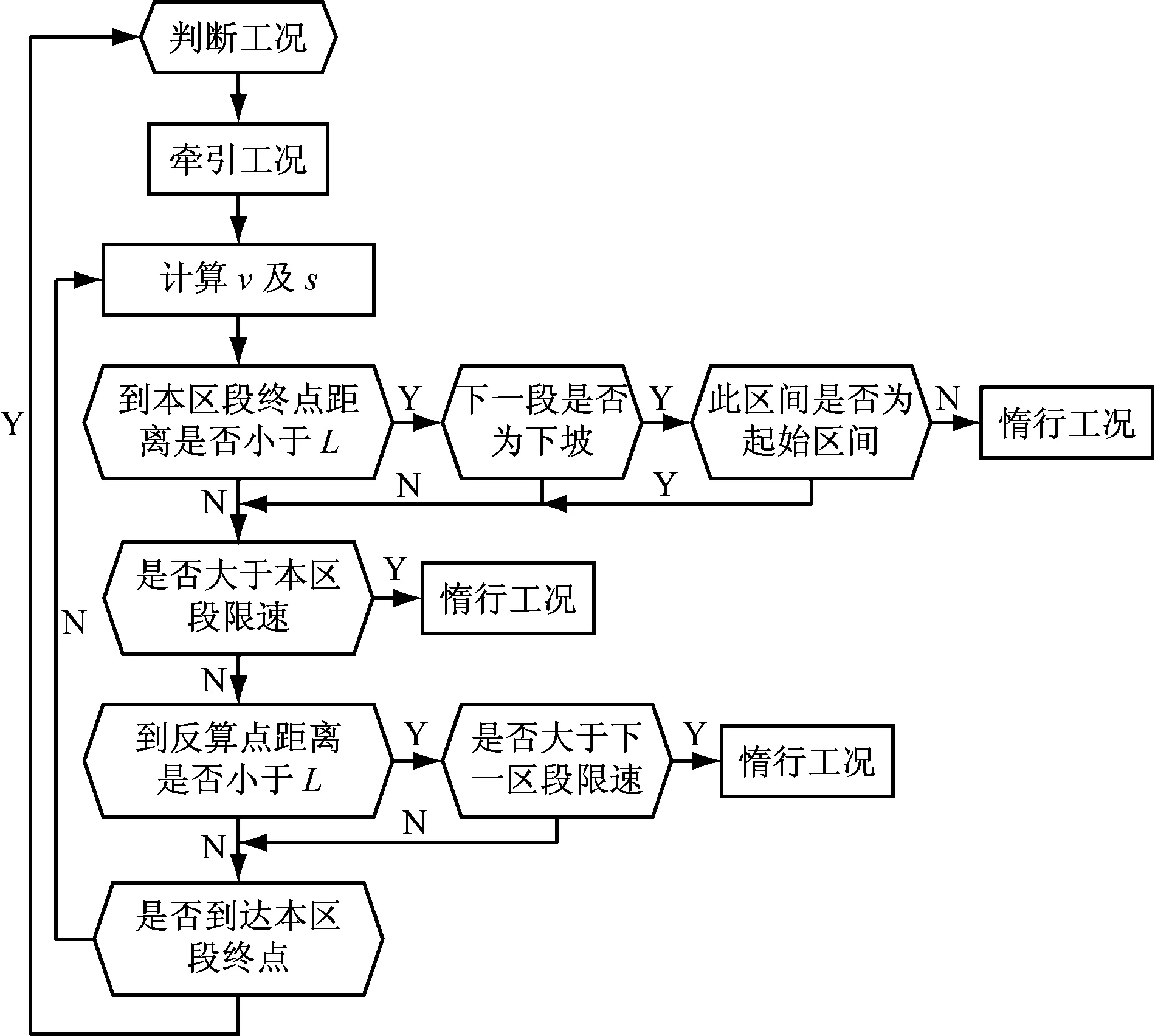
图3 牵引工况控制流程图
3 牵引计算仿真模型验证
牵引仿真计算程序是基于Maltab gui的编程实现及界面设计[7]。程序导入牵引/制动特性曲线,输入列车的质量、编组数、电机数量、最大运行速度,以及线路各区段长度、坡度、曲线半径。经仿真计算,得到列车区间运行时的牵引能耗[8]、平均旅行速度和运行时间。计算结果输出界面如图6所示。

图4 惰行工况控制流程图
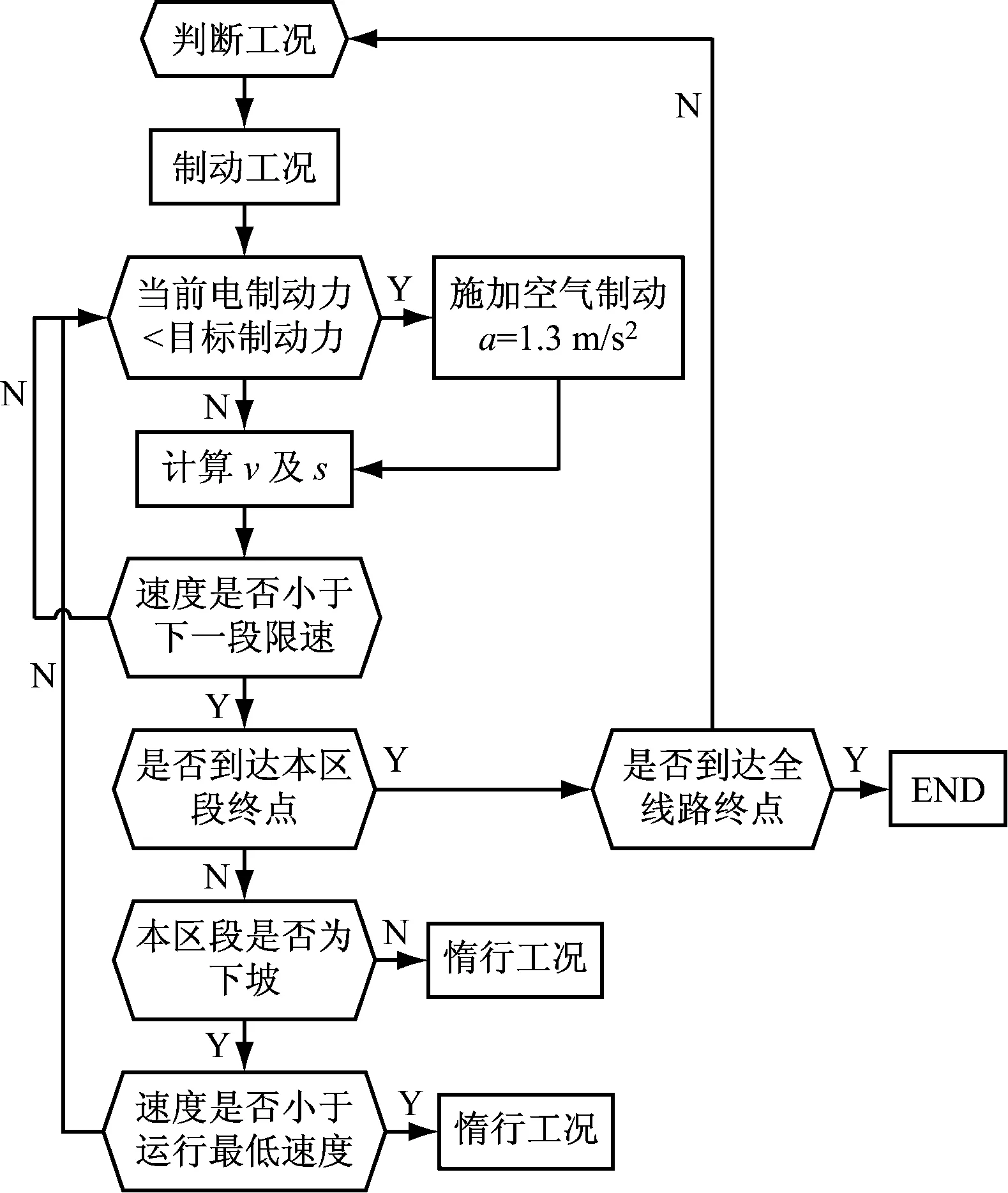
图5 制动工况控制流程图
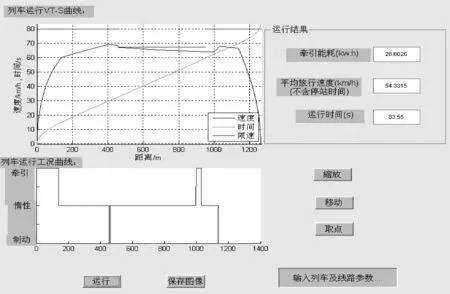
图6 速度-距离曲线及工况曲线输出结果实景图
导入北京S1磁浮线的列车车辆基本参数及线路参数,可得计算结果如表1所示。此计算结果验证了仿真计算模型的适用性。

表1 北京S1磁浮线的牵引仿真计算结果
4 中低速磁浮列车故障工况仿真
北京S1磁浮线列车为6节全动车编组。为验证列车的故障救援能力,对不同故障工况进行牵引计算。计算结果如表2所示。
工况1:载荷为AW3(超载),列车损失1/6动力。
工况2:载荷为AW3,列车损失1/3动力。
工况3:1列6节编组载荷为AW0(空载)、完全动力的列车牵引1列6节编组载荷为AW3、损失完全动力的列车,列车牵引限速为40 km/h。
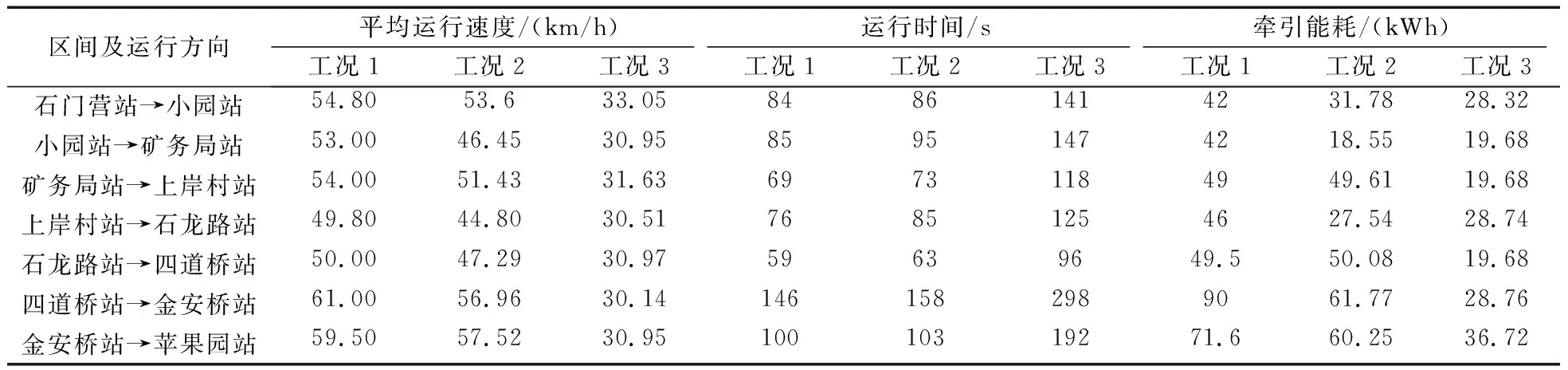
表2 故障工况下的牵引计算结果
仿真结果表明,该模型能满足中低速磁浮列车在故障工况下的牵引仿真计算。
5 结论
分析了磁浮列车的受力情况及运行策略。以北京S1磁浮线为例,仿真计算了磁浮列车在正常运行工况及3种故障工况下的运行情况。计算结果证明,仿真模型能适用于磁浮列车在不同工况下的牵引仿真计算,其仿真结果对运营组织有指导意义。
[1] 罗京, 胡伟, 刘豫湘. 中低速磁浮列车牵引特性分析和计算[J]. 电力机车与城轨车辆, 2010, 33(6): 21.
[2] 张中央, 孙中央. 列车牵引计算[M]. 北京: 中国铁道出版社, 2011.
[3] 郑琼林, 赵佳, 樊嘉峰. 直线电机轮轨交通牵引传动系统[M]. 北京: 中国科学技术出版社, 2010.
[4] 吕喜明, 李明远. 最小二乘曲线拟合的MATLAB实现[J]. 内蒙古民族大学学报(自然科学版), 2009, 24(2): 125.
[5] 饶攀, 刘少克. 低速磁浮列车牵引计算算法研究[J]. 机车电传动, 2012(5): 66.
[6] 胥红敏, 郭湛, 李晓宇. 地铁列车牵引计算算法及程序实现[J]. 现代城市轨道交通, 2011(5): 80.
[7] 罗华飞. MATLAB GUI设计学习手记[M]. 2版. 北京: 北京航空航天大学出版社, 2011.
[8] 桂翔. 城市轨道交通牵引计算仿真系统的开发[J]. 甘肃科技, 2011, 27(13): 124.

