Investigation of SPECT/CT cardiac imaging using Geant4

A.Alfuraih•O.Kadri,2•K.Alzimami

1 Introduction

It is evident that radiation and radioisotopes are routinely used for medical diagnosis,treatment,and management of a wide variety of ailments all over the world.They play a pivotal role in improving the quality of human life.Moreover,the cardiac function,perfusion,and contractibility can be assessed non-invasively by using various techniques such as ultrasound,X-ray computed tomography(CT),single photon emission computed tomography(SPECT),Positron Emission Tomography(PET),etc.All these imaging techniques provide information with diagnostic and prognostic value,and their strengths and limitations have been widely reviewed[1].The combination of both modalities of SPECT and CT during exams,namely SPECT/CT imaging multimodality,has recently emerged as a brilliant diagnostic tool in medical imaging,where anatomical details may delineate functional and metabolic information[2].Consequently,the scientific research community (physicist,doctor,technologist,...)started investigating such fields.Nonetheless,having a complete chain(framework)of tools which are easily accessible,free of charge to be downloaded from the web,expandable and continuously maintained,describing the overall medical imaging procedure is of prime interest to advance our knowledge on the topic.

Furthermore,the accurate medical imaging procedures of the human body are quite challenging for several reasons,especially the existing large number of tissues and organs forming the body.This point reveals the importance of anatomical models in medical imaging procedures.Thus,one must use computational or physical anatomical models to optimize and use a more in-depth study of the different medical imaging scenarios for diagnosis and therapy purposes.

The modelization of computational human phantoms started from primitive shapes(spheres,cylinders,boxes,etc.)to describe different tissues and organs of the body to the more complicated model,called mathematical phantom,based on functional representations and developed since 1967,through the more realistic voxel-based representations starting in 1984[3,4].Actually,there is a more complicated alternative consisting of the so called mesh/polygon based phantoms on grouping voxels for the same region with one polygon[5],which is not yet ready to be included within Monte Carlo simulation programs.

To study the emission and the transmission of photons through the human heart organ,the simulation technique has been proved to be a powerful complement.It has helped to investigate the problem through simple and complex geometry models.From the existing many modern codes(e.g.,MCNP[6],FLUKA[7]),Geant4[8]and its derivative GATE[9,10]engines are commonly applied for those purposes.Such code was used for many medical physics circumstances,such as dosimetry computation during a mammography exam[11],PET,SPECT,and CT[12]scanners,external-beam design.

Another parameter to be taken into account for the simulation of the CT imaging was the X-ray tube output.Nowadays,there exist many X-ray spectra generators providing realistic spectrum for a given set of parameters(kVp, filtration,anode).Also,after accomplishing the simulation of the projected data of the heart phantom submitted to multimodality SPECT/CT imaging procedure,we are intended to perform the reconstruction of such image.From the many existing image reconstruction software,we chosen ImageJ[13]with a specific plugin to accomplish the Filtered Back Projection (FBP)[14]method usually used for this kind of imaging.We chose ImageJ for that purpose due to its Java programming language,allowing it to run on any operating system(Linux,Windows,32 and 64-bits),its free availability on the web,and the continuously maintenance by a large community.

In this work,a sophisticated computational framework,easily accessible for the scientific research community,was proposed to model the overall SPECT/CT cardiac imaging procedures involving the particles tracking histories from their generation source through a voxelized human phantom to the detection zone and the reconstruction of the projected image on the detector.The objective of the present study is to design the full computational framework based on the Monte Carlo simulation technique.Therefore,we first investigated the photon beam generation comprising the internal(for SPECT modality)and the external(for CT modality)exposures.Secondly,we incorporated the High De finition Reference Korean Man(HDRK-Man)[15]voxel data into a developed Geant4-based program using its valuable feature of nested parameterization.Then,we applied the FBP method to the projected simulated images.Thirdly,we studied a more realistic case consisting of the modeling of the GE In finia II 3/8′′Gamma Camera,submitted to a99mTc photon beam(for SPECT imaging)and cone-shaped X-ray beam(for CT imaging)and having different hexagonal hole collimators(low energy high resolution (LEHR),medium energy general purpose(MEGP),and high energy general purpose(HEGP)).

Finally,the application of the proposed framework can be extended to study other imaging modalities and other organs.Also,the possible optimization of different parameters of the imaging procedure,such as the photon source characteristics,the voxelized phantom,and the detection block geometry,can be of great interest for radiation physics researchers,technologists,and doctors.Moreover,such work can be treated for radiation protection and radiotherapy,other than imaging purposes.

2 Materials and methods

In this section,we will first present the usage of the virtually grouped computational framework for an idealized geometry setup that can be useful for academic/teaching purposes.Secondly,we will describe a realistic application that can be useful for the researcher community.

2.1 HDRK-Man geometry simulation

The Monte Carlo simulation toolkit Geant4 version 10.3,written in C++programming language,was used to mimic the particles transport through different compartments of the setup including the detector,the target,and the photon source.The toolkit served a wide variety of user communities for multidisciplinary research fields,such as high-energy physics,space dosimetry,medical imaging,radiation therapy,and radiation protection[8].Regarding the many features of particle tracking models providing detailed information about interactions at any location in the user-defined geometry,large scale of covered energy(from 100 eV to 100 TeV),extendible data base of particle categories(Lepton,Meson,Baryon,Ions,...),handling realistic complicated geometries,different choices of visualization systems(OpenGL,QT,HepRapp,...)[16],and the multithreading opportunity allowing the bene fit of using the multicore computers[17],the Geant4 toolkit seems to be a good candidate for our purpose.

For the current work,we used the voxelized computational phantom of an adult Korean male(HDRK-Man)as a more realistic example other than MIRD[18]or Zubal[19]which are widely used for medical dosimetry purposes.It was constructed from high-resolution photographic anatomical images to represent the Reference Korean Man.The voxelized model is 171 cm in height and 68 kg in weight.The voxelresolution is1.981×1.981×2.0854 mm3,and the model has an array size of 247,141,and 850 in the x,y,and z directions,respectively.For our case,we are limited to about 250 slices,from 850,including the heart organ and the surrounding tissues.The definition of the elemental composition and density obtained from ICRU 46[20]was taken into account,as given in Table 1.Such huge number of voxels was tailored within a Geant4-based program thanks to its nested parameterization feature by the use of the G4VNestedParameterisation class.

2.2 Primary particles generation

2.2.1 Computed tomography

As we intended,to generate the photon beam describing the CT modality,we first generated a clinical X-ray tube output having the specific parameters of 120 kVp and 4.3 mm Al as total filtration(inherent+added).Such X-ray beam spectrum was generated using the Spektr software[21].Moreover,any other X-ray tube beam specifications can be straightforwardly conducted.Then,we applied the inverse transform method[22],based on the computation of the cumulative distribution function,to generate random numbers according to the previously described spectrum.Such results were included within the Primary Generator Action specific class of Geant4.For simplicity purposes,we do not include the full modeling of the CT modality,including the detector dead time,timing,spatial resolution,which in turn can be easily conducted by convolving simulation outputswith specific dedicated functions describing each parameter.Finally,in order to accomplish the CT imaging procedure,we rotated the phantom many times around the Z axis with a regular rotation angle.

2.2.2 SPECT

Starting with the HDRK-Man computational phantom,we extracted the voxel positions,forming the heart wall and its contents.Then,we generated γ-rays having a Gaussian energy distribution of 140.5 keV as the mean and 11.85 keV as the standard deviation,mimicking the99mTc radioisotope energy spectrum.As for the SPECT imaging modality,the incoming beam to the detector(having an energy resolution of about 8.4%at the photopeak of99mTc)was collimated,we simplify our geometry setup by generating parallel photon beams and discarding the collimation.Also,we rotated the phantom around the Z axis with a regular rotation angle.Here also,we did not fully model the imaging chain including the electronic background,spatial resolution,etc.

2.2.3 SPECT/CT

For the multimodality of SPECT/CT,we combined both simulation conditions of SPECT and CT as described separately in the previous subsections.Thus,we randomly shoot the photon energy,isotropically with equal probability,internally from the heart area or externally from outside the phantom.We rotated the phantom 180 times with one degree as a rotation rate and collect the number of particles reaching the detector space.Here,an arrived particle to the detector was considered as primary when its energy becomes within the energy window of primary energy and its standard deviation of 10%(E±10%),or simply using the Geant4 feature of keeping particle tracks along its history allowing us to test the track identification(ID)to see if it is equal to one indicating a primary particle.Notice that the integral uniformity and the differential uniformity values of a field of view of a gamma camera were uniquely impacted by the energy window width[23].

For the current work and for simplicity purposes,we considered that X-ray and γ-Ray photons are generated with equal probability.Thus,after generating a random number(rndm),we generate an X-ray photon if rndm＜0.5 and a γ-Ray if rndm ≥ 0.5.For more realistic cases,and assuming that the X-ray tube emits a certain number of photons(nX-Ray)and the heart zone emits a certain number of photons(nγ-Ray),we should proceed as follows(1):

where

As an application,we compared projected images of the HDRK-Man,at various rotation angles,with combined images resulting from CT and SPECT separately,to those simulated simultaneously(CT and SPECT at the same time).

Table 1 Density and elemental composition of the used organ/tissue materials

2.3 Physical interactions

We used the physical processes describing the photoelectric effect,the Compton and the Rayleigh scattering for photon particles,the Bremsstrahlung and the ionization and the multiple scattering model for electron particles.The energy threshold was set to 1 keV for photons and to 10 keV for electrons,corresponding to about 2μm as production cuts in range.The atomic deexcitation process( fluorescence,Auger electron emission,and PIXE)was activated during the simulation.We selected to use the‘‘Phys List Em Standard’’from the existing suite of physical packages as it is adequate for this kind of Monte Carlo simulation applications.

2.4 Output data analysis

For each case(projection),we collected the number of primary particles reaching the detector zone and the corresponding coordinates on a voxelized detector of 512×512 pixels.Thus,for each run we have a projected image of the HDRK-Man.Then,we used the ImageJ software[13]with the specific plugin ‘‘Radon,’’which is able to perform a radon transform(by using a Filtered Back Projection(FBP)algorithm)on it[24].The analytical method FBP is still the most widely used in clinical applications because of its simplicity,speed,and computational efficiency.The provided filters by such plugin are given by the following equations[25,26]:

Hann/Hamming(x)

where N is the number of samples in the function and α=0.5 and 0.54 are for Hann and Hamming filters,respectively.

where kxand kyare the spatial frequencies.

where f and fmare the spatial frequencies of the image and the cut-off frequency.

2.5 Computational framework components

As shown in Fig.1,the computational framework includes the Geant4-based program,the voxelized phantom database (HDRK-Man),the X-Ray beam generator(Spektr),and the image reconstruction program(ImageJ+Radon plugin).All the carried out simulations were performed using a Dell Precision T7610 Workstation with 40 cores and equipped with an Intel Xeon E5-2680v2 CPU at 2.80 GHz and 256 GB RAM and working on Linux operating system(Ubuntu 14.04).This framework can be run on other operating systems such as Window.The statistical errors related to the photon detections were less than 3%for all calculations carried out.

Fig.1 Proposed computational framework components for this study

2.6 Application for GE In finia II 3/8′′gamma camera

Toward the study of realistic cases,we estimated the scattered energy spectra reaching the head of the GE In finia II 3/8′′gamma camera and quantitatively compared this simultaneously,against combined SPECT/CT imaging of the HDRK-Man phantom using the proposed computational framework.More than 42 runs were carried out for those purposes,including the modeling of the collimator(No collimation,LEHR(low energy high resolution),MEGP(medium energy general purpose),and HEGP(high energy general purpose)),the detector crystal(NaI(Tl)and CZT(cadmium zinc telluride))and different heart organ uptakes to background(1:1,5:1,and 50:1).

2.6.1 Gamma camera geometry and collimators

In order to model a realistic gamma camera,we are referred to the dimensions and the materials used by Garcia et al.[27,28]for simulating the GE In finia II 3/8′′gamma camera.As shown in Table 2,the head shielding,made with 10-mm-thick lead(with an open face in front of the primary beam direction),handles the collimator,the detector crystal,and others.Two variants of crystal material were used:9.5-mm-thick NaI(Tl)with an elemental composition of 0.152(Na),0.838(I),0.01(Tl)and a density of 3.7g/cm3and 5.0-mm-thick CZT with an elemental composition of 0.368(Cd),0.214(Zn),0.418(Te),and a density of 5.78g/cm3[29].Also,we used three different collimators to be compared with each other and without collimation for the current situations.Having regular hexagonal hole distribution,the LEHR,MEGP,and HEGP collimator types differ in the length and the diameter of holes and the septal thickness with values,in mm,of(35,1.5,and 0.2),(58,3.0,and 1.05)and(66,4.0,and 1.8),respectively.An illustrative simulated view of the experimental setup is shown in Fig.2.Moreover,we keep the gamma camera head close to the imaged phantom as interpreted from previous works that the detected energy spectra greatly in fluenced with the phantom/gamma camera head distance[30].On the other hand,as previously,we used a primary beam of 120 kVp and 4.3 mm HVL1to model the CT beam.

2.6.2 Data analysis procedure

In order to ful fill our goal for this part of work,we intend to carry out some statistical quantification of thedifference between simulated simultaneous(here denoted with X)and combined SPECT/CT(here denote with Y)images.Each image has a 512×512 number of pixels(N).Thus,we conducted the calculation of signal-to-noise ratio(SNR),peak signal-to-noise ratio(PSNR),root mean square difference(RMSD),and mean absolute difference(MAD)between X and Y images for different conditions of collimation,uptake,and detector crystal combinations.We bene fit from the ImageJ plugin provided by the Biomedical Imaging Group[31,32].Also,we carried out the calculation of the Structural SIMilarity(SSIM)index using a specific Imagej plugin[33].

Table 2 Characteristics of the simulated gamma camera

Fig.2 Visualization of the simulated setup including a cone beam X-Ray source,a phantom and the GE In finia II 3/8′′gamma camera head(a);rotated gamma camera(b)and zooming on the hexagonal holes collimator(c)

where,σxand,σyare the mean value and the standard deviation of X and Y,respectively,and the parameters are c1=(0.01L)2and c2=(0.03L)2with L=2bitsperpixel-1.

3 Results and discussion

3.1 Ideal case study

Figure 3 shows the overall spectrum of the primary generated particles during the multimodality imaging,including both contributions of the X-Ray beam,for CT modality,and γ-Ray beam,for SPECT modality.For the first part of the curve,we observe the characteristic tungsten element forming the anode of the X-Ray tube.For the second part,we observe the specific spectrum of the99mTc radioisotope fitted with a Gaussian function.The number of particles generated for such curve was 108events.Calculating the area under curves(AUC)for each part gives us a proportion of 4.4%overlap between X-Ray and γ-Ray photons.

Fig.3 Primary generated particles spectrum during SPECT/CT imaging including both contributions of X-Ray and γ-Ray spectra( fitted with a Gaussian curve)for CT and SPECT modalities,respectively.We used Root software for plotting[34]

The overall simulation setup was shown in Fig.4,describing the interaction of some generated photons from outside(CT)and inside(SPECT)the phantom.We observe the source plan from where we generate the parallel beam simulating the CT source.Also,the second more densebeam,located at the middle of the phantom,corresponds to the internal exposure mimicking the injected heart with the99mTc labeled radiopharmaceutical.A three-dimensional view of the phantom was added to Fig.4.We added a realistic view of the phantom into the figure for better setup understanding.The supposed ideal detector,having an energy resolution of 1 keV and 0 s as dead time,was seen behind the phantom.Visualization was carried out using the HepRapp viewer.Each projected image originates from an ascii file consisting of 512×512 integers generated with the Geant4-based developed program.For the attempt to choose an adequate filter for the FBP procedure,we compared the gray intensity characteristics of mean,standard deviation,and minimum and maximum values for the region of interest formed by the heart.We applied such comparison for all the filtered back projected images,and for clarity we show some images of them in Fig.5.All results were summarized in Table 3.It is shown that the application of the Hann filter was better than the others due to its highest values of maximum gray value and the fraction of standard deviation to mean value.

The application of the proposed framework was carried out to quantify the difference,in terms of image data,between simultaneous and combined coregistration.Some difference images are shown in Fig.6.Such differences may be due to the overlapping contribution of X-Ray and γ-Ray photons for simultaneous imaging,causing its double counting during the simulation procedure.Also,not taking into account the full modeling of both imaging modalities(CT and SPECT)can quantitatively contribute to such difference.Table 4 illustrates the gray valuemeasurements of the heart zone taken as the region of interest.It was shown that the highest mean value and the narrowest intensity interval belongs to the rotation angle of 90°,which is logical due to the presences of scattered particles by both lung organs.For tuning purposes,image reconstruction specialists can use iterative methods as an alternative such as MLEM[36],OSEM[37],or ART[38].

Fig.5 FBP image reconstruction with different filtration methods for a given simulated projection

Table 3 Gray value measurements(mean,standard deviation,minimum,and maximum)for a given region of interest including the heart organ(area in pixels)of an image reconstructed with different filtration applied to the FBP technique

Fig.6 Difference image between combined and simultaneous SPECT/CT coregistration for some rotation angles(from the left to the right:0°,45°,and 90°)

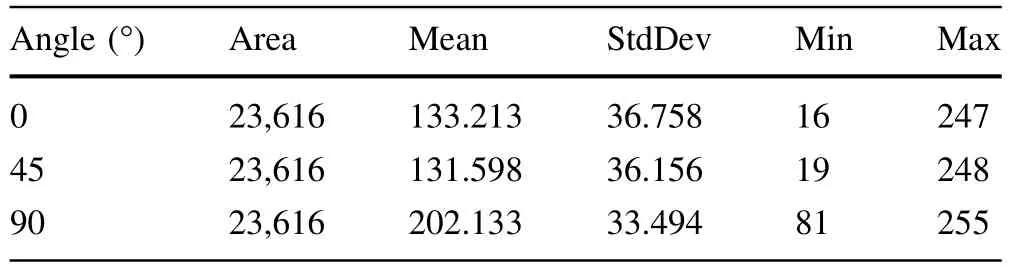
Table 4 Gray value measurements(mean,standard deviation,minimum,and maximum)for a given region of interest(area in pixels)of the difference image between combined and simultaneous SPECT/CT coregistration for some rotation angles

3.2 Realistic case study

For the SPECT/CT imaging of the voxelized phantom,the simulated energy spectra of primary(unscattered),scattered,and total particles reaching the detector crystal of the GE In finia II 3/8′′gamma camera head are shown in Fig.7.They summarize the effect of modifying the type of collimator from LEHR to MEGP and the crystal detector from NaI(Tl)to CZT on the energy response of the gamma camera.The energy spectra result from the interaction of the generated primary particles,namely X-Ray(120 kVp and 4.3 mm HVL1)and Gamma-Ray(99mTc),with the HDRK-Man phantom and the collimator of the gamma camera.We found that MEGP and HEGP behave in a same manner;thus,we plotted only the energy spectra belonging to MEGP other than those for the LEHR collimator.For this case study,we can extract three useful comments:(i)the dedicated collimators for medium and high energy,MEGP and HEGP,are equivalent for the studied energy range(from some keV to 150 keV)(ii)CZT has a lower sensitivity than NaI(Tl)crystal,due to the effective atomic number effect,as previously concluded by Pretorius et al.[39]and Chen et al.[40](iii)the Gaussian fit,using Minuit2 package[41],of the99mTc photopeak demonstrate the higher energy resolution(FWHM=2.355×σ)of the CZT compared to NaI(Tl),with σ values of 14.02 and 14.91,respectively,as also concluded by other works[39,40].

Moreover,Table 5 illustrates the quantification of the statistical difference between simulated simultaneous and combined SPECT/CT images for different combinations of collimator type(LEHR and MEGP),crystal detector(NaI(Tl)and CZT),and99mTc uptake ratio of the heart organ(1:1,5:1,and 50:1).We observed that the combination of the LEHR collimator with NaI(Tl)crystal,generally gives better results.Also,we can see great variation when passing from an LEHR collimator to an MEGP collimator,which in turn was dedicated for the mean energy range(＞120 keV).

For each studied case,the corresponding simulation run time for 1×109generated events was about 3 h 15 minand 15 h 50 min for a 40 CPU Workstation and a 8 CPU Laptop,respectively.

Fig.7 Simulated energy spectra of total(left),primary(middle)and scattered(right)particles reaching the Gamma camera head for simultaneous SPECT/CT imaging of the voxelized phantom.The almost same curves correspond to MEGP(continuous line)and LEHR

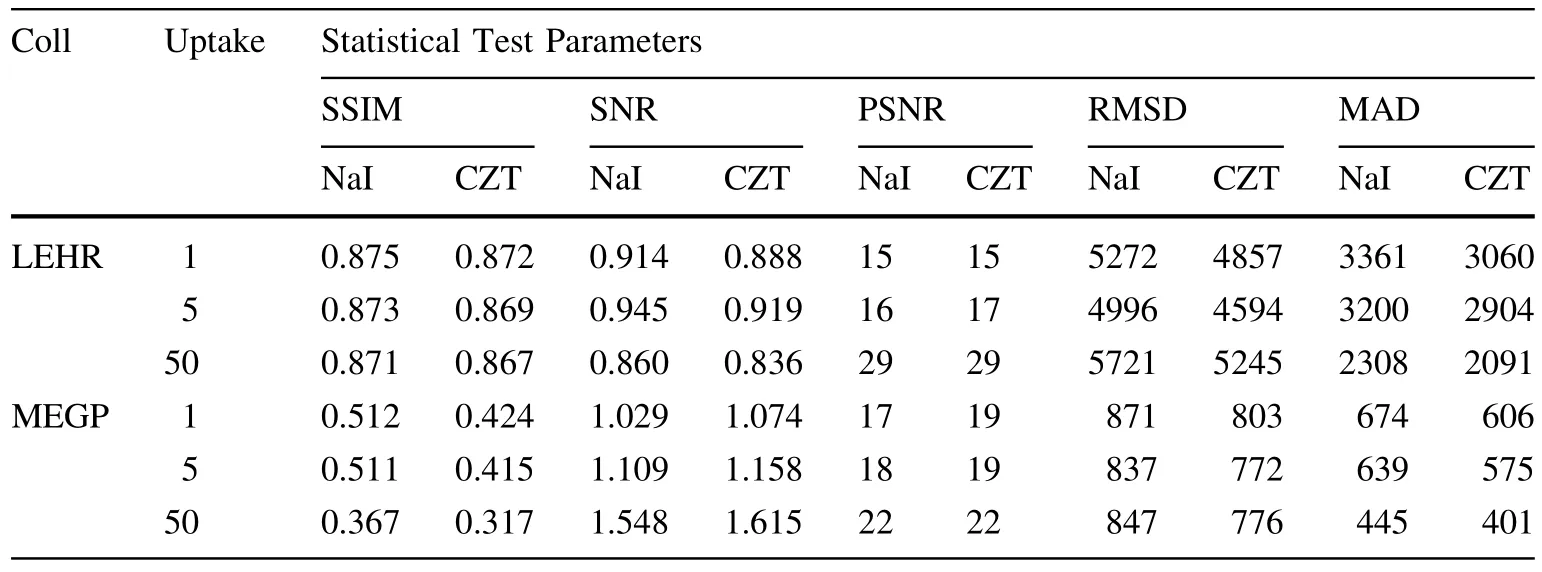
Table 5 Statistical comparison of simulated simultaneous and combined SPECT/CT images for different combinations of collimator type,crystal detector and99mTc uptake ratio of the heart organ,according to equations(6)and(10)

4 Conclusion

We introduced a virtual computational framework for modeling the entire cardiac imaging procedure during SPECT/CT multimodality from the internal exposure due to the injection of99mTc radioisotope,external exposure governed by the X-Ray tube generator,and image acquisition to the final image reconstruction.Also,we incorporated the HDRK-Man voxelized human phantom into a Geant4-based program running in a multithreaded mode.The acceptable reconstructed image,using the ImageJ software,allowed us to conclude that the proposed framework can be applied by physicist researchers,as their components are free and daily-maintained,for other situations and purposes,such as dosimetry,4D(space+time)simulation,PET/CT multimodality,and machine design study and optimization.Furthermore,the usage of such a framework for realistic cases,describing the GE In finia II 3/8′′gamma camera,allowed us to conclude that using the couple of NaI(Tl)as a crystal detector and the LEHR collimator,was the optimal choice for SPECT/CT cardiac imaging.

1.A.H.Gershlick et al.,Role of non-invasive imaging in the management of coronary artery disease:an assessment of likely change over the next 10 years.A report from the British Cardiovascular Society Working Group.Heart 93,423–431(2007).https://doi.org/10.1136/hrt.2006.108779

2.H.Seo et al.,Feasibility study on hybrid medical imaging device based on Compton imaging and magnetic resonance imaging.Appl.Radiat.Isot.67,1412–1415(2009).https://doi.org/10.1016/j.apradiso.2009.02.082

3.W.P.Segars,B.M.Tsui,Study of the efficacy of respiratory gating in myocardial SPECT using the new 4D NCAT phantom.IEEE Trans.Nucl.Sci.49(3),675–679(2002).https://doi.org/10.1109/tns.2002.1039548

4.L.S.Boia et al.,Application of digital image processing for the generation of voxels phantoms for Monte Carlo simulation.Appl.Radiat.Isot.70(1),144–148(2012).https://doi.org/10.1016/j.apradiso.2011.08.017

5.C.H.Kim et al.,The reference phantoms:voxel vs polygon.Ann.ICRP 45(1 Suppl),188–201(2016).https://doi.org/10.1177/0146645315626036

6.D.B.Pelowitz et al.,MCNPX Users Manual Version 2.6.0.LACP-07-1473(Los Alamos National Laboratory,Los Alamos,2007)

7.A.Ferrari et al.,FLUKA:a multi-particle transport code.CERN 2005-10,INFN/TC_05/11,SLAC-R-773(2005)

8.S.Agostinelli et al.,GEANT4-a simulation toolkit Nucl.Instrum.Methods A 506,250–303(2003).https://doi.org/10.1016/S0168-9002(03)01368-8

9.S.Jan et al.,GATE-Geant4 application for tomographic emission:a simulation toolkit for PET and SPECT.Phys.Med.Biol.49(19),4543–4561(2004)

10.F.Zagni et al.,Accurate modeling of a DOI capable small animal PET scanner using GATE.Appl.Radiat.Isot.75,105–114(2013).https://doi.org/10.1016/j.apradiso.2013.02.003

11.O.Kadri et al.,Computation and parameterization of normalized glandular dose using Geant4.Nucl.Sci.Technol.26(030303),1–6(2015).https://doi.org/10.13538/j.1001-8042/nst.26.030303

12.L.Archambaul et al.,Overview of Geant4 Applications in Medical Physics,in Conference:Nuclear Science Symposium Conference Record,2003 IEEE,vol.3.https://doi.org/10.1109/nssmic.2003.1352215

13.C.A.Schneider,W.S.Rasband,K.W.Eliceiri,NIH Image to ImageJ:25 years of image analysis.Nat.Methods 9,671–675(2012).https://doi.org/10.1038/nmeth.2089

14.J.B.Udo et al.,Improved reconstructions and generalized filtered back projection for optical projection tomography.Appl.Opt.50(4),392–398(2011).https://doi.org/10.1364/ao.50.000392

15.C.H.Kim et al.,HDRK-Man:a whole-body voxel model based on high-resolution color slice images of a Korean adult male cadaver.Phys.Med.Biol.53,4093–4106(2008).https://doi.org/10.1088/0031-9155/53/15/006

16.A.John et al.,The Geant4 visualization system—a multi-driver graphics system.Int.J.Model.Simul.Sci.Comput.04,1340001(2013).https://doi.org/10.1142/s1793962313400011

17.J.Allison et al.,Recent developments in GEANT4.Nucl.Instrum.Methods Phys.Res.A 835,186–225(2016).https://doi.org/10.1016/j.nima.2016.06.125

18.A.Ma et al.,Absorbed fractions in the revised MIRD head phantom calculated using MCNPX.J Nucl.Med.54(2),1032(2013)

19.I.G.Zubal et al.,Computerized three-dimensional segmented human anatomy.Med.Phys.21,299–302(1994).https://doi.org/10.1118/1.597290

20.ICRU,Photon,Electron,Proton and Neutron Interaction Data for Body Tissues ICRU Report No 46(International Commission on Radiation Units and Measurement,Bethesda,MD,1992)

21.J.Punnoose et al.,Technical note:spektr3.0—a computational tool for x-ray spectrum modeling and analysis.Med.Phys.43(8),4711–4717(2016).https://doi.org/10.1118/1.4955438

22.O.Kadri et al.,Incorporation of the Goudsmit–Saunderson electron transport theory in the Geant4 Monte Carlo code.Nucl.Instrum.Methods Phys.Res.B 267,3624–3632(2009).https://doi.org/10.1016/j.nimb.2009.09.015

23.H.C.Kim et al.,Comparison of image uniformity with photon counting and conventional scintillation single-photon emission computed tomography system:a Monte Carlo simulation study.Nucl.Eng.Technol.49(4),776–780(2017).https://doi.org/10.1016/j.net.2016.12.002

24.P.A.Toft,J.A.Srensen,The Radon Transform—Theory and Implementation(Kgs.Lyngby,Denmark:Technical University of Denmark (DTU),1996).http://orbit.dtu.dk/ files/5529668/Bin der1.pdf

25.M.Lyra,A.Ploussi,Filtering in SPECT image reconstruction.Int.J.Biomed.Imaging,vol.2011,Article ID 693795(2011).https://doi.org/10.1155/2011/693795

26.F.J.Harris,On the use of windows for harmonic analysis with the discrete Fourier transform.Proc.IEEE 66,51(1978).https://doi.org/10.1109/proc.1978.10837

27.M.-P.Garcia et al.,TestDose:a nuclear medicine software based on Monte Carlo modeling for generating gamma camera acquisitions and dosimetry.Med.Phys.42(12),6885–6894(2015).https://doi.org/10.1118/1.4934828

28.M.-P.Garcia et al.,Accelerated GPU based SPECT Monte Carlo simulations.Phys.Med.Biol.61(11),4001–4018(2016).https://doi.org/10.1088/0031-9155/61/11/4001

29.http://www.webqc.org/molecular-weight-of-CdZnTe.html.Accessed 20 May 2017

30.M.Ashoor et al.,Evaluation of Compton attenuation and photoelectric absorption coefficients by convolution of scattering and primary functions and counts ratio on energy spectra.Indian J.Nucl.Med.30(3),239–247(2009).https://doi.org/10.4103/0972-3919.158532

31.http://bigwww.ep fl.ch/sage/soft/snr.Accessed 25 May 2017

32.R.C.Gonzalez,R.E.Woods,Digital Image Processing,3rd edn.(Prentice Hall,Englewood Cliffs,2008).ISBN:013168728

33.Z.Wang et al.,Image quality assessment:from error visibility to structural similarity.IEEE Trans.Image Process.13(4),600–612(2004).https://doi.org/10.1109/tip.2003.819861

34.R.Brun,F.Rademakers,ROOT—An Object Oriented Data Analysis Framework,in Proceedings AIHENP’96 Workshop,Lausanne,Sep.1996,Nucl.Inst.&Meth.in Phys.Res.A,vol.389, p. 81–86 (1997). https://doi.org/10.1016/S0168-9002(97)00048-X

35.J.Allison et al.,The GEANT4 visualisation system.Comput.Phys.Commun.178,331–365(2008).https://doi.org/10.1016/j.cpc.2007.09.010

36.P.P.Bruyant,Analytic and iterative reconstruction algorithms in SPECT.J.Nucl.Med.43(10),1343–1358(2002)

37.S.M.Kim et al.,Fully three-dimensional OSEM-based image reconstruction for Compton imaging using optimized ordering schemes.Phys.Med.Biol.55(17),5007–5027(2010).https://doi.org/10.1088/0031-9155/55/17/009

38.R.Gordon,R.Bender,G.T.Herman,Algebraic reconstruction techniques(ART)for three-dimensional electron microscopy and x-ray photography.J.Theor.Biol.29(3),471–81(1970).https://doi.org/10.1016/0022-5193(70)90109-8

39.P.H.Pretorius et al.,Monte Carlo simulations of the GE discovery alcyone CZT SPECT systems.IEEE Trans.Nucl.Sci.62(3), 832–839 (2015). https://doi.org/10.1109/TNS.2015.2433533

40.L.Chen,Y.-X.Wei,Monte Carlo simulations of the SNM spectra for CZT and NaI spectrometers.App.Radiat.Isot.66,1146–1150(2008).https://doi.org/10.1016/j.apradiso.2008.01.008

41.F.James,M.Roos,Minuit:a system for function minimization and analysis of the parameter errors and correlations.Comput.Phys.Commun.10,343–367(1975).https://doi.org/10.1016/0010-4655(75)90039-9