(001)面双轴应变锗材料的能带调控
,, ,,,(., 508; .工程学院软件学院, 508; ., 6005)
1 前 言
随着半导体行业的快速发展,半导体器件特征尺寸将不断减小,逐渐达到物理和技术上的双重极限,集成电路的集成度将很难再按照摩尔定律的规律向前发展。因此,我们需要研究开发新的材料、新的器件结构、新的生产工艺以满足高速处理信息能力的需求[1]。一方面,由于Ge材料的电子和空穴的迁移率均比Si高,科学家们提出利用Ge材料作为MOSFET(Metal-Oxide-Semiconductor Field-Effect-Transistor)的沟道材料以进一步提高微电子器件的性能[2];另一方面,人们发现,Ge材料具有准直接带特性[3],通过张应变、掺杂等能带改性攻略可以将它调控为准直接带隙半导体,因此在光电子材料与器件的开发方面,Ge材料具有潜在的应用价值;同时,Ge与传统的Si工艺兼容性好,在工业生产方面具有价格优势。
近年来,国内外许多研究机构试图利用Ge材料的准直接带特性开发相应的器件用于硅基光电集成,并在实验方面对(001)面双轴应变Ge材料与器件的制备技术进行了大量的报道。例如,利用Ge与Si、SiGe、GeSn等晶格失配和热失配的原理[4-6],在外延Ge材料时引入一定量的双轴应变,进而改善材料的光电特性;在新器件开发方向,主要集中于报道双轴张应变Ge材料在发光及探测方面的潜在应用[7-9];并且美国MIT研究小组[10](2012年首次报道)和德国Roman Koerner等研究人员[11](2015年报道)先后报道了Si基双轴张应变Ge室温电泵激光器,证实了双轴张应变Ge材料作为激光器增益介质的可靠性。然而,目前制备得到的激光器存在着阈值电流过高,器件工作不稳定等缺点,有待进一步从理论研究、材料生长和器件结构设计等方面进行优化设计。
在理论计算方面,国内外对应变Ge材料的报道主要可以分为两个方面,一是采用k.p理论计算单轴应变Ge材料的价带结构[12-13],二是采用第一性原理或基于实验参数与经验公式的理论方法等计算张应变Ge材料的能带结构[14-18],并预测Ge材料转变为直接带半导体所需要施加的张应变值。Ge半导体的禁带宽度与应变之间的关系对材料设计、器件模拟等方面具有重要的理论参考价值,目前在这方面报道较少。本文基于形变势理论详细对(001)面双轴应变Ge材料的能带结构进行理论计算。首先分析了应变对Ge晶体对称性的影响,然后构建应变Ge材料导带结构、价带结构以及带隙的相关数值模型,最后得到了Ge半导体的禁带宽度与应变之间的函数关系式。
2 模型的构建
2.1 应变对Ge晶体对称性的影响
晶体的对称操作与系统的哈密顿量相互关联,通过分析晶体的对称性也能够获得半导体能带结构的一些重要特征。选择合适晶向或晶面对晶体施加适当的单或双轴应变可以改变晶体结构的对称性,因此,通过分析半导体晶体结构的对称性是研究应变对半导体能带结构影响的有效而又直观的方法之一。
根据形变势理论[19-21],半导体材料所受到的应变可以分解为剪切应变和静水应变,其中,剪切应变又可以分为两类,一类剪切应变与x、y和z方向上的晶格常数的改变密切相关,另一类剪切应变与晶体的旋转相关。对于立方晶系半导体而言,剪切应变降低了晶体的对称性,从而导致了能带的退简并以及能带的弯曲;而静水应变不改变晶体的对称性,因此它的作用仅仅使能带发生偏移,不会清除能带的简并性。

图1 (001)面双轴张应变面心立方晶体的晶格常数模型Fig.1 Lattice constant model of face-centered cubic structure under biaxial strain paralleled to the (001) plane

综上所述,如果我们用Ec和Eν两个物理量表示Ge的各个导带底和价带顶的位置,那么对于Ge材料在(001)面双轴张应变作用下的能带分裂情况可以用图2表示。

图2 (001)面双轴张应变锗材料的能带分裂示意图Fig.2 Schematic of band splitting of Ge under biaxial strain paralleled to the (001) plane
图2中显示,对于双轴张应变锗材料,静水应变使得导带底和价带顶发生了能量偏移;而剪切应变对价带而言发生了能带分裂现象,同时对其不同方向的导带底也产生了不同的影响,具体为,对L和Г能谷不影响,而Δ能谷则分裂为Δ2和Δ4能谷。
2.2 应变Ge导带模型
对于(001)晶面双轴应变Ge材料,导带能谷不仅有退简并的可能,即:六度简并的Δ能谷将退简并为Δ2和Δ4能谷,四度简并的L能谷和无简并的Г能谷不发生退简并;而且存在偏移的现象。根据形变势理论,在平行于(001)晶面的双轴应变作用下,锗材料导带L能谷、Г能谷及Δ能谷的偏移量可以表示为[14]:
(1)
(2)
(3)
(4)

由此,我们可以得到(001)晶面双轴应变Ge材料各导带底能级的位置:
(5)


表1 应变Ge材料能带计算相关参数Table 1 Band parameters and deformation potentials for Ge under biaxial strain paralleled to the (001) plane
2.3 应变Ge价带模型
由形变势理论可知,Ge材料在平行于(001)晶面的双轴应变作用下,价带将发生退简并的现象,如果考虑自旋轨道的影响,三个价带相对于未应变Ge的情况,其能带的分裂能差分别表示为[19-20]:
价带轻空穴带:
Δ0δE+9/4(δE)2]1/2
(6)
价带重空穴带:
(7)
价带自旋轨道能带:
Δ0δE+9/4(δE)2]1/2
(8)
式中:Δ0表示自旋轨道分裂能;δE=2b(ε⊥-ε‖);b表示价带在应力作用下的形变势能,具体参数值见表1,单位为eV。
由此,我们可以得到(001)晶面双轴应变Ge材料价带顶能级的位置:
(9)
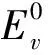
综上所述,得到了Ge材料导带能带和价带能带与应变之间的联系,并且建立了它们之间的具体关系表达式,这些为建立Ge材料在应变作用下的能带结构模型提供了基础。
3 结果与讨论
由应变对Ge导带能带和价带能带影响的具体表达式就可以建立Ge材料在应变作用下的能带结构模型。基于形变势理论,在应变的作用下,半导体材料的能带带隙可以写成:
(10)


图3 Ge导带各能谷的偏移量随应变的变化趋势Fig.3 Various strain components in conduction of biaxial strained Ge paralleled to the (001) plane as a function of in-plane strain
图3给出了(001)晶面双轴应变Ge材料导带L能谷、Г能谷、Δ2能谷及Δ4能谷的偏移量随应变的变化趋势。从图中可知,双轴应变使得导带间接带L能谷发生偏移,偏移量与应变呈线性递减的关系,即每增加1%的应变则间接带L能谷下降44.9meV。具体地,相比于无应变Ge情况,在张应变的作用下,L能谷往低能方向移动;在压应变的作用下,它将往高能方向移动。对于直接带Г能谷,同样只存在能级偏移的情况,并且偏移规律与L能谷类似,但每增加1%的应变则直接带Г能谷下降121.7meV,Г能谷往低能方向偏移的速度比L能谷快1.71倍,这意味着在一定的张应变条件下,Ge将从间接带隙材料变为以Г能谷为最低能级的直接带隙半导体材料。导带的Δ能谷,在(001)晶面双轴应变作用下由未应变前的六度简并分裂为一组二度简并Δ2能谷和一组四度简并Δ4能谷。其中Δ2能谷的偏移量随应变的变化的规律与直接带Г能谷几乎一致。而Δ4能谷的变化情况与其它能谷正好相反,即相比于无应变Ge情况,每增加1%的应变则Δ4能谷上升45.7meV,具体为在张应变的作用下,Δ4能谷往高能方向移动,在压应变的作用下,它将往低能方向移动。
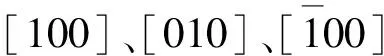
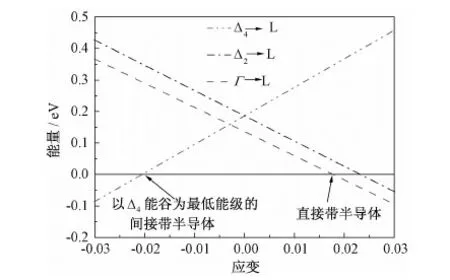
图4 Ge导带Г能谷、Δ2能谷及Δ4能谷与L能谷的差值和应变之间的关系Fig.4 Energy differences between Г valley、Δ2 valley、Δ4 valley and L valley in biaxial strained Ge paralleled to the (001) plane as a function of in-plane strain
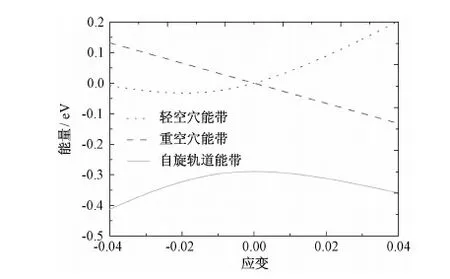
图5 (001)晶面双轴应变Ge材料各个价带能级的分裂与偏移情况Fig.5 Splitting energy of valence band in biaxial strained Ge paralleled to the (001) plane as a function of in-plane strain
图5给出了(001)晶面双轴应变Ge材料各个价带能级的分裂与偏移情况。从图中可见,轻、重空穴在双轴应变的作用下发生了退简并,重空穴能量的偏移与应变呈线性递减关系,每增加1%的应变则重空穴能级下降32.9meV;具体地,相比于无应变Ge情况,在张应变的作用下,重空穴能级往低能方向移动,在压应变的作用下,它将往高能方向移动。而轻空穴能级随着张应变的增大向高能方向移动,随着压应变的增大先向低能方向移动,当压应变增大到约2%后转向高能量方向移动。自旋轨道能带的变化趋势为:均随着张、压应变的增大而呈现非线性的向低能方向减小。
价带轻、重空穴的退简并不仅可以减小价带空穴的有效质量而且也减小了空穴在轻、重空穴带之间的散射几率,从而提高价带空穴的迁移率,因此应变有利于Ge沟道MOSFET器件获得更高的性能。

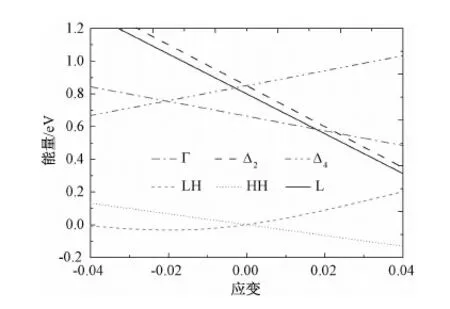
图6 Ge在(001)晶面双轴应变下能带偏移情况 Fig.6 Various band edge shifts as a function of in plane strain for biaxial strained (001) Ge
由于在双轴应变的作用下,Ge的价带轻、重空穴发生了退简并,压应变下相对于无应变Ge材料,重空穴会向高能量方向偏离原来位置,而轻空穴会向低能量方向偏离原来位置;而张应变情况下正好相反,因此Ge材料各个能谷的能带宽度计算方法应该为:压应变情况下计算各个导带底到重空穴能带顶的位置,而张应变情况为计算各个导带底到轻空穴能带顶的位置。据此,我们得到Ge材料各个能谷的能带宽度与应变的关系如图7所示。计算结果表明在(001)面双轴应变作用下,锗的能带结构发生了重要的变化:室温下锗的禁带宽度与应变的关系可以用分段函数来表示,如式(11)所示。
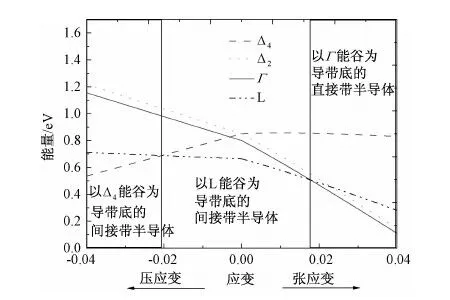
图7 Ge材料各个能谷的能带宽度与应变的关系Fig.7 Various band gap as a function of in plane strain for biaxial strained (001) Ge
(11)
当压应变增加到2.06%时,Ge材料将被调控为以Δ4能谷为导带底的间接带半导体,此时室温下Ge材料的禁带宽度约为0.688eV,随着压应变的增大,禁带宽度线性减小,具体为每增加1%的压应变,禁带宽度减小约78.63meV。当张应变增加到1.77%时,Ge材料被调控为以Г能谷为导带底的直接带隙半导体,禁带宽度为0.5077eV,随着张应变的增大,禁带宽度线性减小,即每增加1%的张应变,禁带宽度减小177.98meV。而应变介于-2.06%和1.77%时,Ge材料是以L能谷为导带底的间接带半导体,无应变Ge材料在室温下的禁带宽度为0.664eV,禁带宽度随着压应变增加而线性增加,即每增加1%的压应变,禁带宽度增加11.66meV,增加幅度较小;禁带宽度随着张应变增加而线性减小,每增加1%的张应变,禁带宽度减小88.29meV。
由于目前实验室制备较高应变的Ge材料比较困难,而且应变条件下Ge材料的禁带宽度也鲜有报道,我们将计算得到的理论值与其他研究小组的计算结果进行比较,如表2所示。主要比较的项目为Ge材料被调控为以Г能谷为导带底的直接带隙半导体和被调控为以Δ4能谷为导带底的间接带隙半导体所需要施加的具体应变值。
从文献报道来看,各个研究小组的研究方法主要可归为两类:一是采用第一性原理计算能带。该方法不需要任何经验参数与实验数据就能计算得到能带结构,但从报道的结果看出,交换关联势的选择会明显影响计算结果,且该方法难与实验结果进行比较。二是采用半经验式的方法,如紧事缚近似、k·p微扰理论等。该方法基于实验参数与经验公式,相比于第一性原理的计算方法,其计算极值点附近的能带结构已足够精确,计算值更接近于实验结果。我们的计算基于形变势理论,依赖于实验参数,因此与文献[14,17]等结果比较吻合;同时也与文献[15]中用密度泛函理论(DFT)计算得到的Ge从间接带隙材料转变为直接带隙材料的所施加的张应变值一致,但由于DFT理论没有考虑Δ能谷的退简并,因此导致他们计算得到的Ge材料转变为以Δ能谷为导带底的间接带半导体条件(3%压应变)偏大。由于实验中难以制备较高应变的Ge材料,导致计算得到的Ge材料带隙转变所施加的应力值结果缺乏实验数据的验证,还存在争议,有待进一步的实验研究。

表2 本文计算的理论值与文献报道结果的对比Table 2 Comparison of calculated results from literature with various theory
4 结 论
基于形变势理论研究了(001)面双轴应变Ge材料的能带结构。计算结果表明:导带L能谷、Г能谷与双轴应变呈线性递减的变化关系,并且Г能谷往低能方向偏移的速度比L能谷快1.71倍,该结论表明,当张应变大于1.77%时,Ge材料被调控为直接带隙半导体,可为制备锗直接带发光器件提供理论指导依据。锗导带Δ能谷以及价带轻、重空穴在双轴应变的作用下发生退简并现象;一方面,当压应变大于2.06%时,Ge材料被调控为间接带半导体,以Δ能谷为导带底,禁带宽度随着压应变每增加1%而线性减小7.863eV,这说明压应变锗材料可用于制备MOSFET器件,以进一步提高导带电子的迁移率;另一方面,价带的退简并有利于提高空穴迁移率,对制备高迁移率的锗电子器件具有重要的理论意义。当对锗施加的应变介于-2.06%和1.77%时,Ge是以L能谷为导带底的间接带半导体,禁带宽度随着压应变每增加1%而增加11.66meV,增加幅度较小;禁带宽度随着张应变每增加1%,而线性减小84.5meV。由于目前实验室得到的锗材料应变值基本介于此区间,该结果对分析目前的实验结果能起到相应的指导作用。
[1] Asghari M, Krishnamoorthy A V. Silicon Photonics: Energy-efficient Communication [J]. Nature Photonics, 2011, 5(5): 268~270.
[2] Goley P S,Hudait M K. Germanium Based Field-effect Transistors: Challenges and Opportunities [J]. Materials, 2014, 7(3): 2301~2339.
[3] Liu J F, Kimerling L C, Michel J. Monolithic Ge-on-Si Lasers for Large-scale Electronic-photonic Integration [J]. Semiconductor Science and Technology, 2012, 27(9): 094006-1~094006-13.
[4] Mitard J, Jaeger B D, Leys F E,Hellings G. Record ION/IOFFPerformance for 65nm Ge pMOSFET and Novel Si Passivation Scheme for Improved EOT Scalability [C]. 2008 IEEE International Electron Devices Meeting. San Francisco, California, USA:IEEE, 2008: 873~876.
[5] Pillarisetty R, Chu K B, Corcoran S, Dewey G. High Mobility Strained Germanium Quantum Well Field Effect Transistor as the p-channel Device Option for Low Power (Vcc=0.5 V) III-V CMOS Architecture [C]. 2010 IEEE International Electron Devices Meeting. San Francisco, California, USA:IEEE, 2010: 6.7.1~6.7. 4.
[6] Han G, Su S, Zhan C, Zhou Q. High-mobility Germanium-tin (GeSn) p-channel MOSFETs Featuring Metallic Source/drain and Sub -370℃ Process Modules [C]. 2011 IEEE International Electron Devices Meeting, Washington, DC, USA: IEEE, 2011: 16.7.1~16.7.3.
[7] Huang S, Lu W, Li C, et al. A CMOS-compatible Approach to Fabricate an Ultra-thin Germanium-on-insulator with Large Tensile Strain for Si-based Light Emission[J]. Optics Express, 2013, 21(1): 640~646.
[8] 黄诗浩,李成,陈城钊,等. N型掺杂应变Ge发光性质 [J]. 物理学报, 2012, 61(3): 036202-1~036202-8.
[9] 吴政,王尘,严光明,等. 采用Al/TaN叠层电极提高Si基Ge PIN光电探测器的性能[J].物理学报, 2012, 61(18): 186105-1~186105-6.
[10] Camacho A R, Cai Y, Patel N, et al. An electrically pumped germanium laser [J].Optics Express, 2012, 20 (10): 11316~11320.
[11] Koerner R, Oehme M, Gollhofer M, et al. Electrically Pumped Lasing from Ge Fabry-Perot Resonators on Si [J]. Optics express, 2015, 23(11): 14815~14822.
[12] 马建立,张鹤鸣,宋建军.单轴应力锗能带结构研究 [J]. 中国科学:物理学 力学 天文学, 2012, 42: 15~21.
[13] Moussavou M, Cavassilas N, Dib E, Bescond M. Influence of Mechanical Strain in Si and Ge p-type Double Gate MOSFETs [C]. 2015 International Conference on Simulation of Semiconductor Processes and Devices. Washington, DC, USA: IEEE, 2015: 373~376.
[14] Kurdi M E, Fishman G, Sauvage S, Boucaud P. Band Structure and Optical Gain of Tensile-Strained Germanium Based on a 30 Band K* P Formalism [J]. Journal of Applied Physics, 2010, 107: 013710-1~013710-7.
[15] Tahini H, Chroneos A, Grimes R WSchwingenschlogl U, Dimoulas A. Strain-Induced Changes to the Electronic Structure of Germanium [J]. J Phys Condens Matter, 2012, 24: 195802-1~195802-4.
[16] Yang C H, Yu Z Y, Liu Y M, et al. Dependence of Electronic Properties of Germanium on the In-plane Biaxial Tensile Strains [J]. Physica B: Condensed Matter, 2013, 427: 62~67.
[17] Chang G E, Cheng H H. Optical Gain of Germanium Infrared Lasers on Different Crystal Orientations [J]. Journal of Physics D: Applied Physics, 2013, 46: 065103-1~065103-14.
[18] Liu L, Zhang M, Hu L J, et al. Effect of Tensile Strain on the Electronic Structure of Ge: A First-Principles Calculation [J]. Journal of Applied Physics, 2014, 116: 113105-1~113105-6.
[19] Walle C G,Martin R M. Theoretical Calculations of Heterojunction Discontinuities in the Si/Ge System [J]. Physical Review B, 1986, 34(8): 5621~5634.
[20] Walle C G. Band Lineups and Deformation Potentials in the Model-Solid Theory [J]. Physical Review B, 1989, 39(3): 1871~1883.
[21] Sun Y, Thompson S E, Nishida T. Physics of Strain Effects in Semiconductors and Metal-oxide-semiconductor-field-effect Transistors[J].Journal of Applied Physics, 2007, 101(10): 104503-1~104503-22.
[22] Ishikawa Y, Wada K, Liu J. Strain-Induced Enhancement of Near-Infrared Absorption in Ge Epitaxial Layers Grown on Si Substrate [J]. Journal of Applied Physics, 2005, 98(1): 013501-1~013501-9.

