多体系统动力学Lie群微分-代数方程约束稳定方法*
李亚男 李博文 丁洁玉,2† 潘振宽
(1.青岛大学数学与统计学院,青岛 266071) (2.青岛大学计算力学与工程仿真研究中心,青岛 266071) (3.青岛大学计算机科学技术学院,青岛 266071)
引言
多体系统动力学通常由微分-代数方程描述,其数值积分方法的研究是计算多体系统动力学研究的重要内容.该领域微分-代数方程求解的传统方法由常微分方程数值求解拓展而来,研究的重点是通过约束稳定达到微分-代数方程求解的稳定[1,2].
近年来逐渐发展起来的保结构几何数值积分方法[3]则通过保持连续系统尽量多的不变量以提高数值计算的稳定性,如辛算法[4]、能量方法[5,6],及基于离散力学变分原理的能量、辛保持的变分数值积分方法[7,8]、Lie群方法[9]等.其中,Lie群方法致力于保持物体姿态的特殊正交群特性,而其他方法主要针对物体姿态的参数化表达,如用经典的Euler角、Bryant角等,相应的算法不能保持物体姿态固有的Lie群特性.
直接用特殊正交群表达物体姿态可有效避免参数化表达导致的奇异性,但由于群空间的非矢量特性,传统的数值积分方法不能直接应用.Simo等[10,11]较早提出在其矢量Lie代数上设计算法,从而保持姿态矩阵的正交性,以达到提高数值稳定性的目的.相关基础论研究是指针对矩阵微分方程的CG方法[12]和MKRK方法[13].前者基于第二类正则坐标,即离散Lie代数矢量,并已用于设计基于指标3的微分-代数方程的广义-α方法设计[14].后者基于第一类正则坐标,即离散计算伪转动角度增量,且被应用于指标1的微分-代数方程的Runge-Kutta方法设计[15].
本文主要针对Lie群表达的多刚体系统动力学微分-代数方程指标1、2和3形式,设计约束稳定方法,使位移约束、速度级约束和加速度级约束同时精确保持,从而提高仿真精度.
1 Lie群表达的数学模型
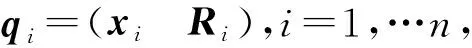
多体系统动力学方程可在Lie群空间表达为如下指标3 微分-代数方程:
(1)

(2)
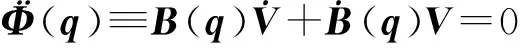
(3)
利用方程(2)和方程(3),Lie群表达的指标2和指标1微分-代数方程形式分别为:
(4)
(5)
方程(1),(4)和(5)均只包含了约束方程、速度级约束方程或者加速度级约束方程,使用不同的数值方法求解时只能精确保持一种约束方程.为了在计算过程中同时保持三种约束方程使其不发生违约,本文对上述微分-代数方程进行改进.
2 Lie群微分-代数方程约束稳定方法
引入Lagrange乘子参数μ,ω,构造新的Lie群表达微分-代数方程如下:
(6)
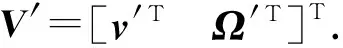
(7)
(8)

(9)
此时方程(6)离散为:
(10)
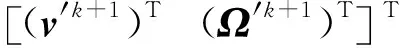
由初始条件x1,v1,Ω1,R1使用牛顿迭代方法迭代求解可以得到xk,vk,Ωk,k=2,3,…,从而由式(9)可得Rk,k=2,3,….
3 数值算例
图1为双连杆空间机械臂,设杆1的质量为m1=5kg,质心坐标为(x1,y1,z1),杆长为l1=1m;杆2的质量为m2=5kg,质心坐标为(x2,y2,z2),杆长为l2=1m.
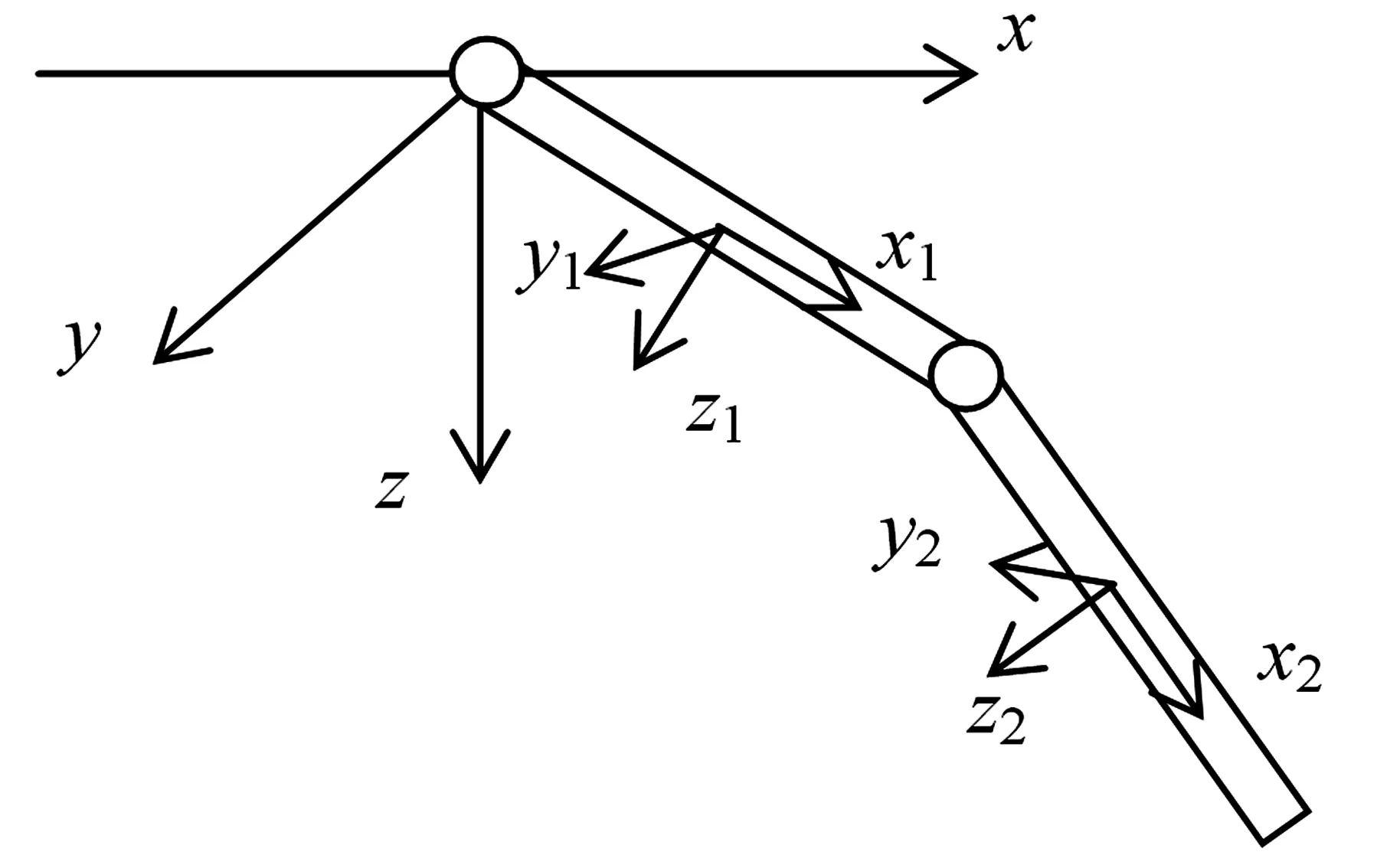
图1 双连杆空间机械臂Fig.1 Two-link space manipulator
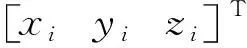
Φ1(q)=x1+R1X10
Φ2(q)=x1+R1X11-x2-R2X21
(11)

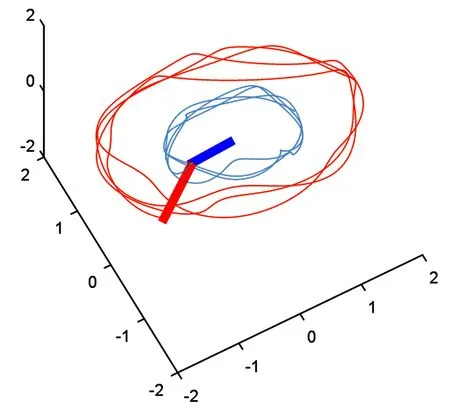
图2 两连杆末端运动轨迹Fig.2 Trajectories of the ends of the two links
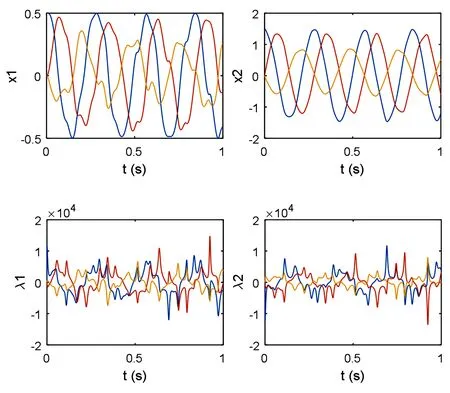
图3 两连杆质心位置和Lagrange乘子Fig.3 Displacements of the mass center of the two links and the Lagrange multipliers
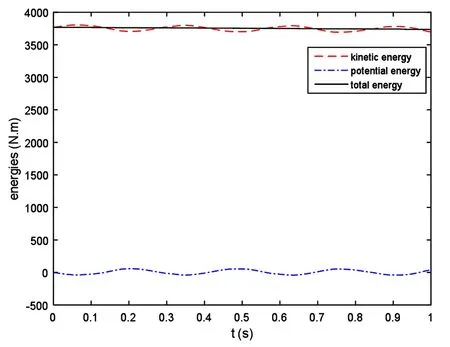
图4 双连杆空间机械臂能量Fig.4 Energies of the two-link space manipulator
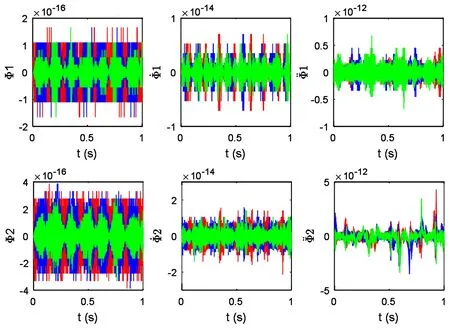
图5 双连杆空间机械臂约束Fig.5 Constraints of the two-link space manipulator
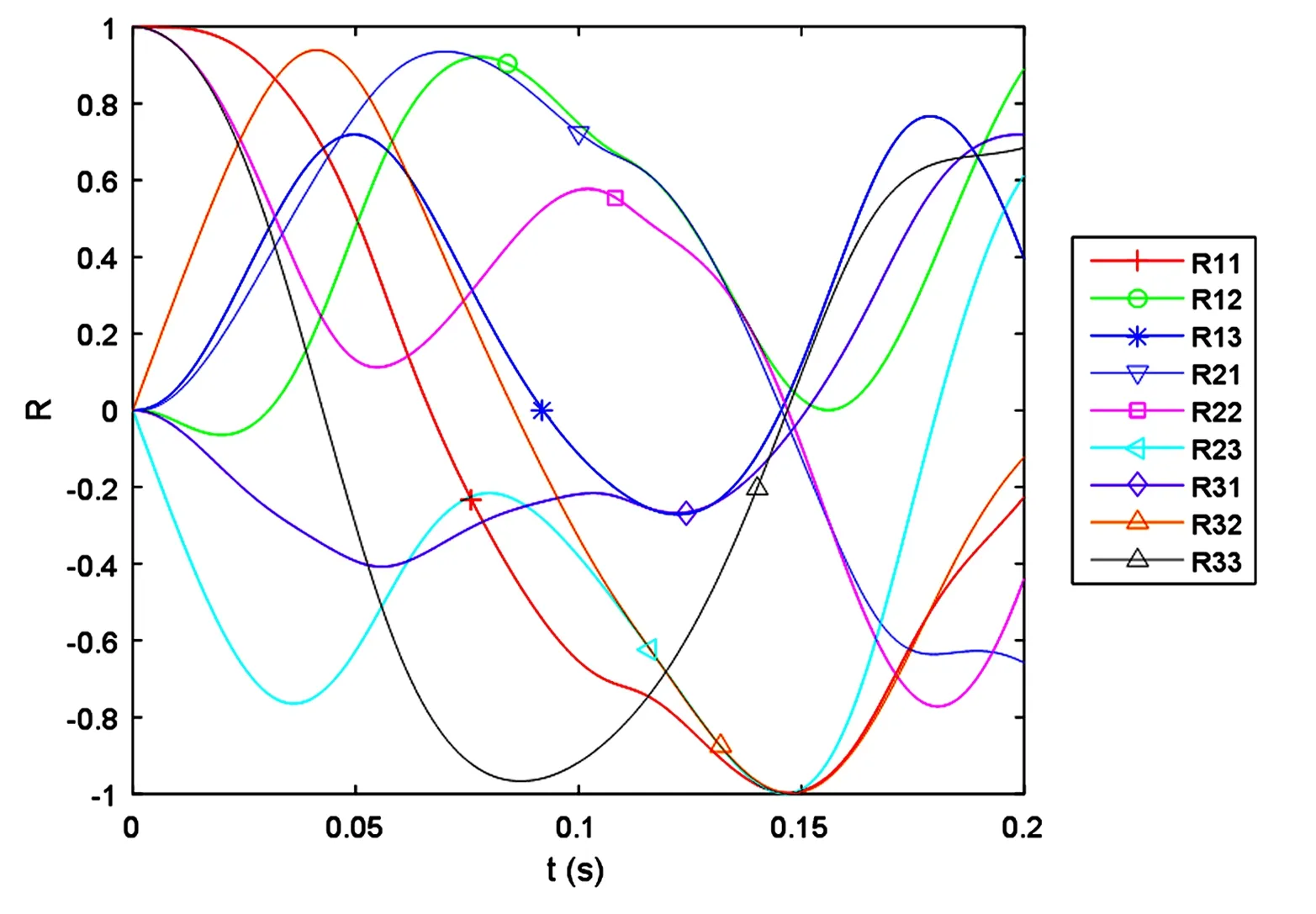
图6 约束稳定方法得到的旋转矩阵各分量Fig.6 Rotation matrix components obtained by using constraints stabilization method
图2给出了仿真过程中的连杆末端轨迹,图3为连杆质心位置和Lagrange乘子λ的时间历程图.从图中可以看到仿真过程稳定.图4为双连杆空间机械臂系统动能、势能和总能量变化图,可以看出系统总能量守恒.图5为系统所受约束方程(11)及相应的速度级约束和加速度级约束时间历程图,可以看出各级约束均精确保持,且精度较高,从而验证了约束稳定方法的作用.图6和图7给出了约束稳定方法得到的旋转矩阵R的各分量变化图及误差eR=RTR-I,进一步验证了约束稳定方法对旋转矩阵R的正交性的保持,即Lie群结构的保持.
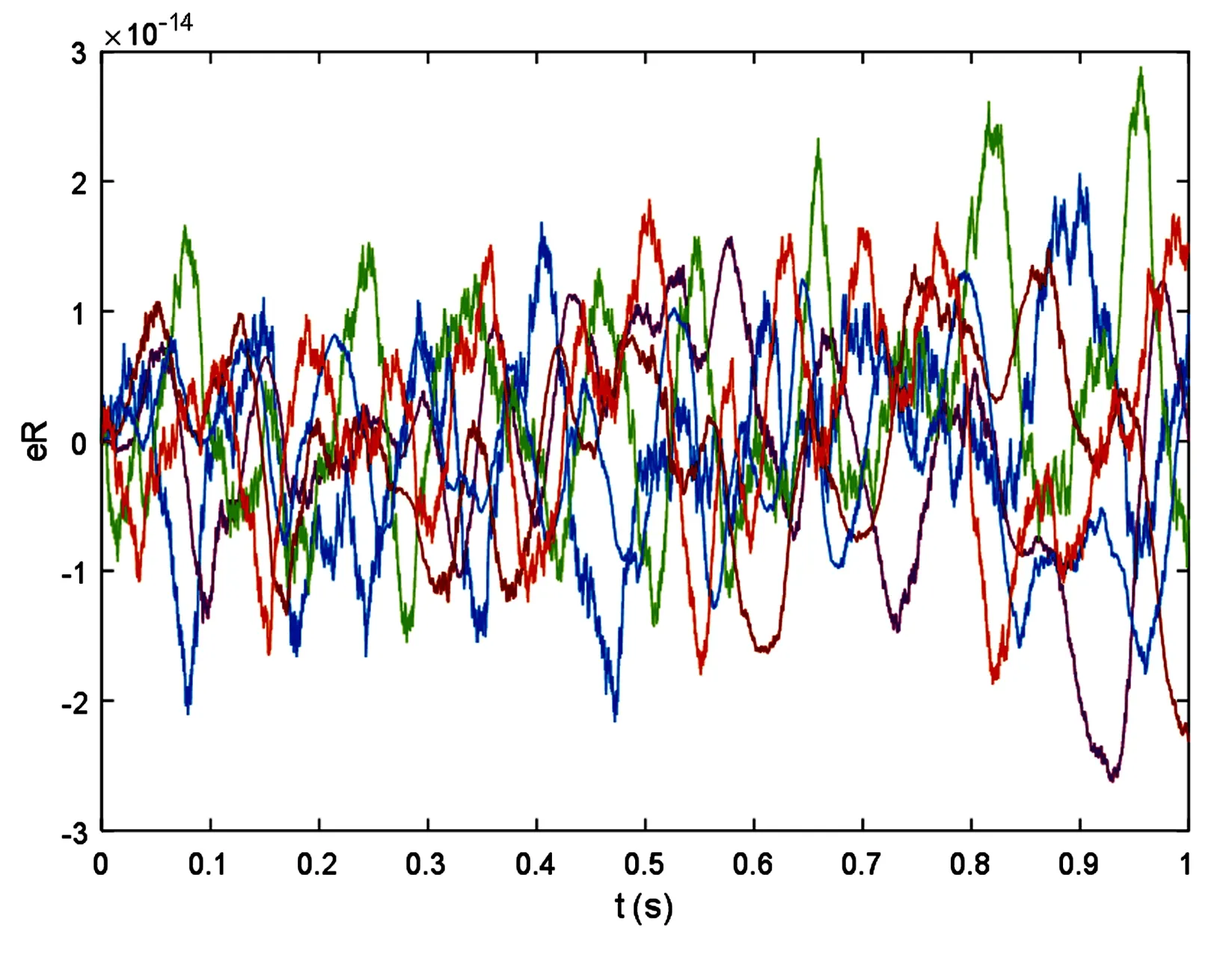
图7 约束稳定方法得到的旋转矩阵正交性误差Fig.7 Errors of the orthogonality of the rotation matrix obtained by using constraints stabilization method
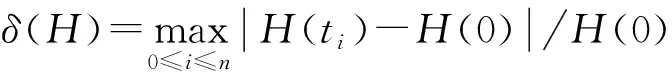

表1 约束稳定方法与指标1、2、3DAEs结果比较(h=0.00001)Table 1 Comparison of the results obtained by constraints stabilization method and index 1,2,3 DAEs (h=0.00001)

表2 约束稳定方法与指标1、2、3DAEs结果比较(h=0.0001)Table 2 Comparison of the results obtained by constraints stabilization method and index 1,2,3 DAEs (h=0.0001)
从表1中可以看出,对指标1微分-代数方程使用隐式方法求解,可以精确保持加速度级约束,但是位移约束和速度级约束误差较大;对指标2微分-代数方程使用隐式方法求解,可以精确保持速度级约束,而位移约束和加速度级约束产生违约;对指标3微分-代数方程求解,可以精确保持位移约束,而速度级约束和加速度级约束误差较大.但是使用约束稳定方法求解,可以同时精确保持位移约束、速度级约束和加速度级约束.另外,从系统总能量相对误差比较可以看出,约束稳定方法的能量误差与指标2方法误差接近,小于另外两种方法.这四种方法得到的系统总能量相对误差变化图如图8所示,可以看出约束稳定方法在保持各级约束稳定的同时,也减小了系统总能量误差. 从表2可以看出,当步长增大时,上述分析仍然成立,与表1比较可以得出,步长增大时,各结果误差有不同程度的增加,其中加速度约束误差增加明显,说明该类方法中加速度约束对步长变化较为敏感.
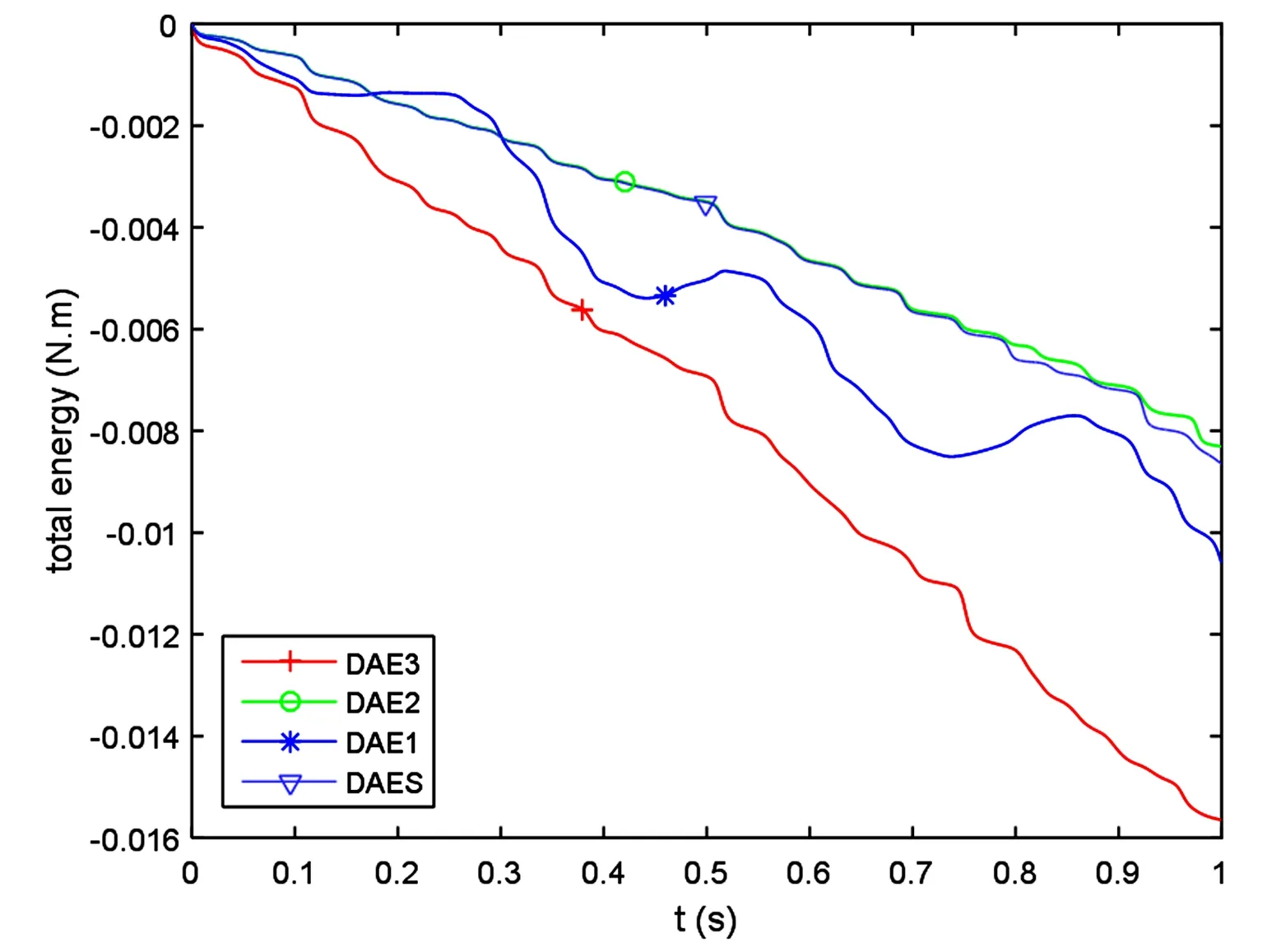
图8 使用不同方法得到的系统总能量Fig.8 Total energies of the system obtained by using different methods
4 结论
本文针对Lie群表达的多体系统动力学微分-代数方程,设计了约束稳定的求解方法,使仿真过程中位移约束、速度级约束和加速度级约束能够同时得到保持.数值算例表明,相比较使用同样向后差商隐式方法求解的指标1、指标2和指标3微分-代数方程,约束稳定方法得到的结果更为精确,在保持各级约束方程的同时,也保持了旋转矩阵的正交性,是一种保Lie群结构的数值方法.在该方法的基础上可以很方便地设计高阶数值方法,进一步提高结果精度.
1Simenon B. Computational flexible multibody dynamics—A differential algebraic approach. Berlin:Springer, 2013
2Fon-Llagunes J M. Multibody dynamics-computational methods and applications. Switzerland:Springer, 2016
3Betsch P. Structure-preserving integrators in nonlinear structural dynamics and flexible multibody dynamics. Switzerland:Springer, 2016
4Jay L O. Symplectic partitioned Runge-Kutta methods for constrained Hamiltonian systems.SIAMJournalonNumericalAnalysis, 1996,33(1): 368~387
5Lens E, Cardona A. An energy preserving/decaying scheme for nonlinearly constrained multibody systems.MultibodySystemDynamics, 2007,18(3):435~470
6Betsch P, Uhlar S. Energy-momentum conserving integration of multibody dynamics.MultibodySystemDynamics, 2007,17(4):243~289
7Marsden J E, West M. Discrete mechanics and variational integrators.ActaNumerica, 2003,10(1):357~514
8Ding J Y, Pan Z K. Higher order variational integrators for multibody system dynamics with constraints.AdvancesinMechanicalEngineering, 2014,6(1):383680-1-8
9Iserles A, Munthe-Kaas H Z, Nørsett S, et al. Lie-group methods.ActaNumerica, 2016,9(2):215~365
10 Simo J C, Vu-Quoc L. On the dynamics in space of rods undergoing large motions—A geometrically exact approach.ComputerMethodsinAppliedMechanicsandEngineering, 1988,66(2):125~161
11 Lewis D, Simo J C. Conserving algorithms for the dynamics of Hamiltonian systems on Lie groups.JournalofNonlinearScience, 1994,4(1):253~299
12 Crouch P E, Grossman R. Numerical integration of ordinary differential equations on manifolds.JournalofNonlinearScience, 1993,3(1):1~33
13 Munthe-Kaas H. High order Runge-Kutta methods on manifolds.AppliedNumericalMathematics, 1999,29(1):115~127
14 Arnold M, Brüls O, Cardona A. Error analysis of generalized-α Lie group time integration methods for constrained mechanical systems.NumerischeMathematik, 2015,129(1):149~179
15 Terze Z, Müller A, Zlatar D. Lie-group integration method for constrained multibody systems in state space.MultibodySystemDynamics, 2015,34(3): 275~305

