存在有限导流断层的复合油藏试井模型及井底压力动态分析

曾 杨, 康晓东, 唐恩高, 谢晓庆, 未志杰

( 1. 中国海洋石油集团有限公司 海洋石油高效开发国家重点实验室,北京 100028； 2. 中国海洋石油集团有限公司 中海油研究总院有限责任公司,北京 100028 )

0 引言

非封闭断层分为部分连通断层和有限导流断层。大部分研究针对部分连通断层边界[1]，对有限导流断层的研究较少，用现有的试井模型解释油田实际资料时拟合效果欠佳。有限导流断层的试井模型既要考虑流体通过断层面，又要考虑流体沿着断层面流动，断层提高储层区域内的泄油能力，且当断层的导流能力达到一定值时，表现出定压边界的特征[2-5]。

人们在非封闭断层试井模型方面进行研究。Bixel H C[6]建立线性复合油藏中岩石和流体性质在界面发生突然变化的试井解释模型。Yaxley L M[7]引入特殊传导率，建立复合油藏中存在部分连通断层的试井解释模型。Ambastha A K等[8]引入Everdingeen A F[9]和Hurst W[10]提出的无限小表皮概念，研究复合油藏中存在部分连通断层边界的井底压力响应特征。Boussila A K等[11]建立天然裂缝性油藏中存在部分连通断层的试井解释模型。Abbaszadeh M等[12]利用点源函数方法，建立考虑断层内部流体流动的有限导流断层与储层耦合模型，但是忽略断层内部流体的压缩性，计算过程复杂，不能保证计算精度。张望明等[13]引入偏移函数概念，建立存在一条线性局部连通断层边界的复合油藏试井解释模型。廖新维[14]考虑接触面附加阻力，建立多区复合油藏试井模型。刘启国等[15]针对双重介质径向复合油藏，在界面连接条件中引入界面表皮概念并建立数学模型，分析界面表皮对典型曲线的影响。罗建新等[16]建立两区线性复合油藏渗流模型，仅考虑储层和流体性质在横向上发生突变，没有考虑线性垂直半渗透边界的影响。

这些研究主要存在三方面问题：一是多数针对部分连通断层，对有限导流断层研究相对较少；二是存在有限导流模型的求解需要通过两边油藏流量与断层内部流量进行耦合，求解过程复杂，数值运算困难；三是存在有限导流模型研究只针对均质油藏，未考虑复合油藏。

笔者运用数学物理方法、渗流力学理论，考虑断层内部流体流动，建立两区复合油藏中存在有限导流断层的试井解释模型；采用Fourier指数变换和Laplace变换方法对模型进行求解，利用计算机编程绘制井底压力响应特征曲线并分析影响因素，为存在类似边界条件的复合油藏试井资料解释提供指导。

1 渗流模型

1.1 假设条件

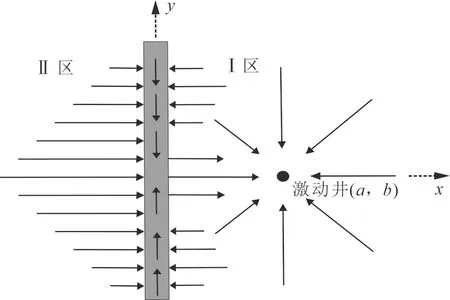
图1 两区无限大复合油藏中存在有限导流断层的流动模型Fig.1 The flow model of finite diversion fault exists in the two-zone infinite compound reservoir

两区无限大复合油藏中存在有限导流断层的流动模型见图1，其中a、b为井点横、纵坐标。

假设条件：

(1)断层两侧的岩石特性、储层厚度及渗透率不同，同一区域内为均质油藏且各向同性，各区的孔隙度和渗透率等地层参数不随压力变化；

(2)油藏流体为单相微可压缩液体，压缩系数及黏度系数不变，流动服从达西定律；

(3)激动井为定产量线源；

(4)考虑井筒储集效应和表皮效应；

(5)引入界面表皮概念，考虑两个储层区域之间断面的传导率；

(6)忽略重力和毛管力的影响。

1.2 模型建立

以基本渗流力学理论为依据，推导两区无限大复合油藏中存在有限导流断层的无因次试井解释模型。

(1)渗流微分方程

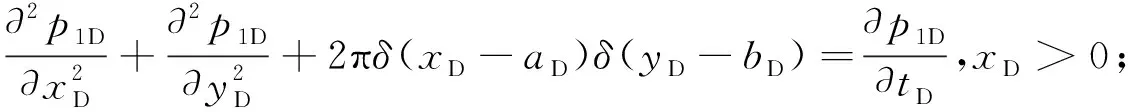
(1)

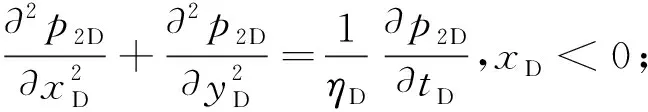
(2)

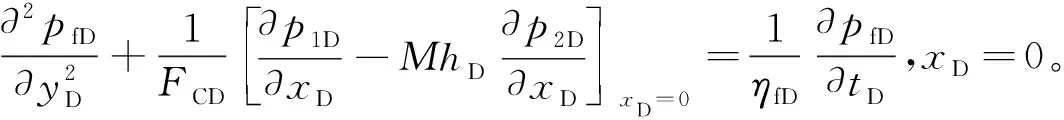
(3)

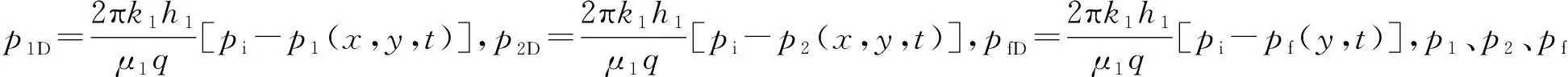
(2)初始条件

p1D(xD,yD,0)=p2D(xD,yD,0)=pfD(yD,0)=0。

(4)

(3)边界条件

p1D(∞,yD,tD)=p2D(-∞,yD,tD)=p1D(xD,±∞,tD)=p2D(xD,±∞,tD)=pfD(±∞,tD)=0。

(5)

(4)连接条件

(6)

(7)

式中：S为表皮因数。

1.3 模型求解

对无因次试井模型式(1-7)进行基于yD的Fourier指数变换和基于tD的Laplace变换，化简可得

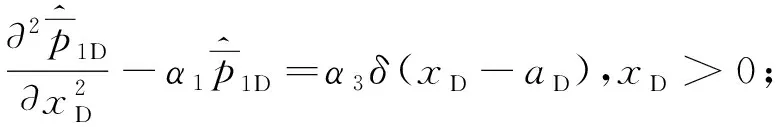
(8)

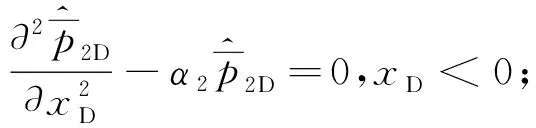
(9)

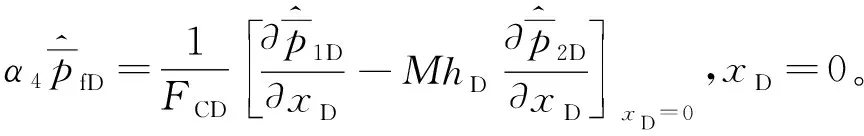
(10)

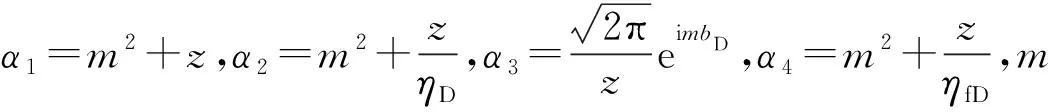
将初始条件、边界条件及连接条件代入式(8-10)，求解得

(11)

(12)

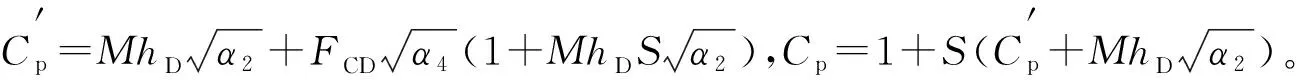
将α3代入式(11-12)并进行Fourier逆变换得

(13)

(14)

令xD=aD-1，yD=bD，生产井的井底压力为

(15)

2 井底压力响应特征曲线及其影响因素

根据井底压力表达式(15)，采用Stehfest数值反演方法进行Laplace逆变换[17-18]，利用计算机编程，绘制两区无限大复合油藏中存在有限导流断层边界的井底压力响应特征曲线，并分析主要影响因素。

2.1 无因次断层导流能力

无因次断层导流能力FCD对压力响应特征曲线的影响见图2。由图2可以看出，典型曲线表现为早期井储阶段和Ⅰ区系统径向流阶段的特征。随着tD增大，压力波传播到两区分界面处，由于分界面处存在界面表皮效应，流体流动阻力增加，压力导数曲线上升。界面表皮的影响结束后，当FCD=0时，断层内部对流体的流动几乎没有影响，随着tD增大，曲线逐渐恢复为无限大地层径向流的特征，表现为0.5的水平线。当FCD>0时，断层内部的渗透率大于两侧储层的渗透率，流体流动能力增加，压降减小，压力导数曲线出现下凹，且FCD越大，曲线下凹越多。当FCD足够大时，压力导数曲线表现为斜率为-1的特征，类似于定压边界的反应。随着断层内部压降的增加，流体逐渐从储层流入断层，并沿着断层面流动，表现为双线性流的特征，压力导数曲线变为斜率为1/4的直线，断层的影响与有限导流垂直裂缝的相似。

2.2 界面表皮效应

界面表皮因数S对压力响应特征曲线的影响见图3。由图3可以看出，典型曲线表现为早期井储阶段的特征，无因次压力与压力导数曲线重合，表现为斜率为1的直线。随着压力波不断向外传播，当tD较小时，压力波尚未传播到两区分界面，地层中表现出均质储层渗流特征，压力导数曲线表现为0.5的水平线，阶段持续时间取决于aD。随着tD增大，压力波传播到两区分界面，当S=0时，分界面处无压降，压力导数曲线继续表现为0.5的水平线。之后，当断层内部的渗透率大于两侧储层的渗透率，压力导数曲线下凹，由于FCD取值足够大，压力导数曲线表现为斜率为-1的特征。当S>0时，Ⅰ区与Ⅱ区的连通性减弱，流体在地层中流动的压力损失增大，压力导数曲线逐渐从0.5的水平线开始上翘，且S越大，曲线上翘越多。当S足够大时，压力导数曲线上升到1的水平线，表现为封闭断层的特征。S越大，曲线下凹越晚，相应的FCD对曲线的影响越小。

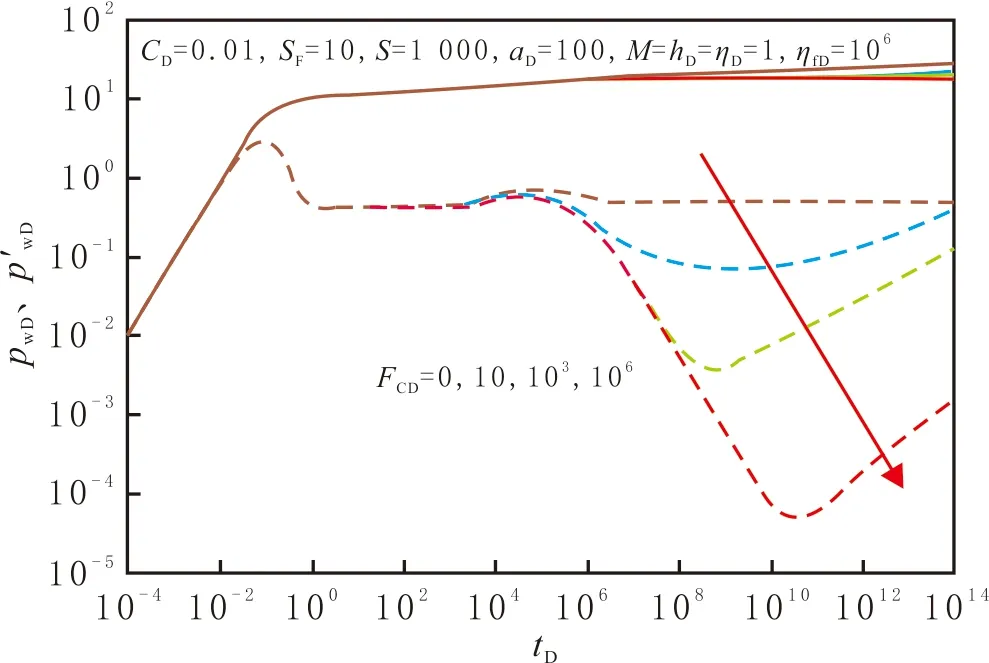
图2 无因次断层导流能力对压力响应特征曲线的影响

Fig.2 Effects ofFCDon the calculated dimensionless type curves

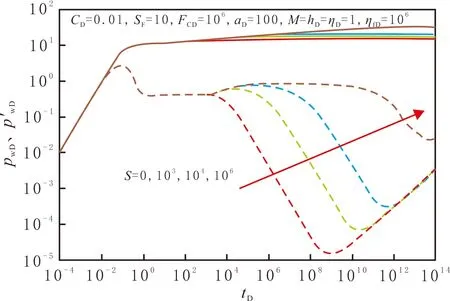
图3 界面表皮因数对压力响应特征曲线的影响Fig.3 Effects of S on the calculated dimensionless type curves

2.3 无因次断层导压系数

无因次断层导压系数ηfD对压力响应特征曲线的影响见图4。由图4可以看出，经过井储阶段和Ⅰ区径向流阶段，压力波传播到两区分界面，由于存在界面表皮效应，流体流动的阻力增加，流动消耗的压降增加，无因次压力及压力导数曲线位置升高。之后，由于分界面断层的渗透率高于两区地层的渗透率，流体流动性变好，压力导数曲线表现出下降的特征，曲线下降幅度取决于ηfD。ηfD越小，断层内部的储集能力越大，压力导数曲线越靠下。随着断层内部压降的增加，流体逐渐从储层流入断层，并沿着断层面流动，表现为双线性流的特征，压力导数曲线变为斜率为1/4的直线，直线出现时间取决于ηfD，ηfD越大，直线出现越早。

2.4 流度比、厚度比、导压系数比

流度比M对压力响应特征曲线的影响主要表现在无因次断层导流能力FCD较小时，当FCD=0时，分析流度比对典型曲线的影响。M对井底压力动态的影响主要发生在压力波传播到两区分界面后(见图5)。由图5可以看出，当M>1时，Ⅱ区物性变好，地层的平均流动性变好，流体在地层中流动的压力损失越小，无因次压力及压力导数曲线降低，且流度比越大，压力及压力导数曲线的位置越靠下。厚度比hD与流度比M对井底压力动态的影响类似(见图6)。由图6可以看出，hD越大，Ⅱ区地层供给能力越强，流体在地层中流动的压力损失越小，反映等效均质储层径向流的第二个压力导数水平段位置越低。导压系数比ηD对典型曲线形态的影响主要发生在压力波传播到两区分界面后(见图7)。由图7可以看出，ηD越小，Ⅱ区的储集能力越大，压降越小，相应的压力及压力导数曲线位置越靠下。

3 实例分析

对某油田的生产井进行压力恢复测试。该井在测试前以250.80 m3/d的产量生产1 240.30 h。生产井井径为0.10 m，有效厚度为35.90 m，孔隙度为0.17，综合压缩系数为1.87×10-3MPa-1，原油黏度为0.80 mPa·s，体积因数为1.31，关井前井底流压为22.40 MPa。

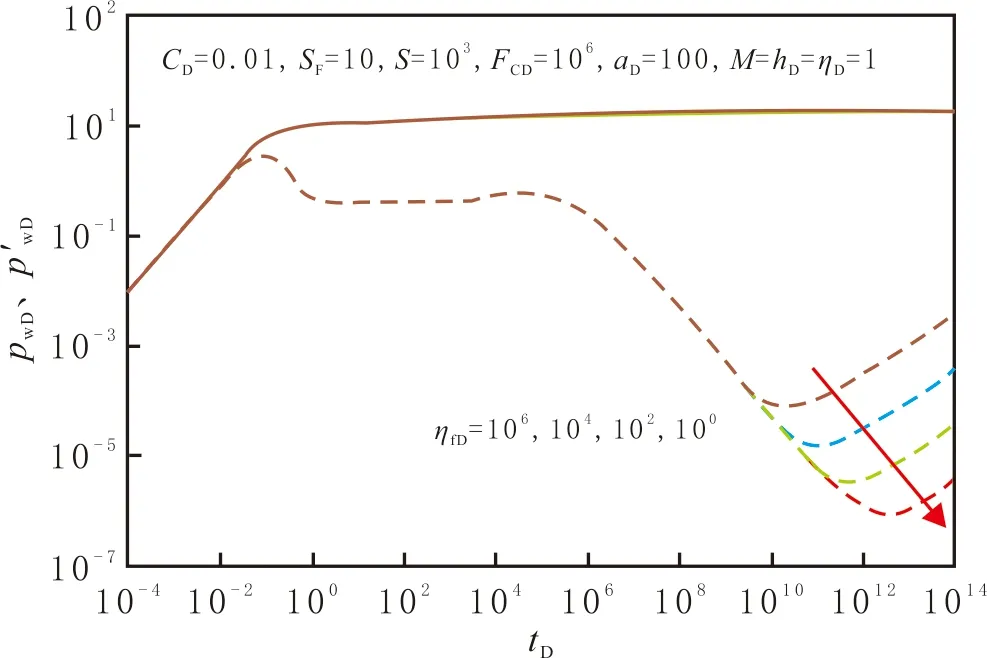
图4 无因次断层导压系数对压力响应特征曲线的影响

Fig.4 Effects ofηfDon the calculated dimensionless type curves

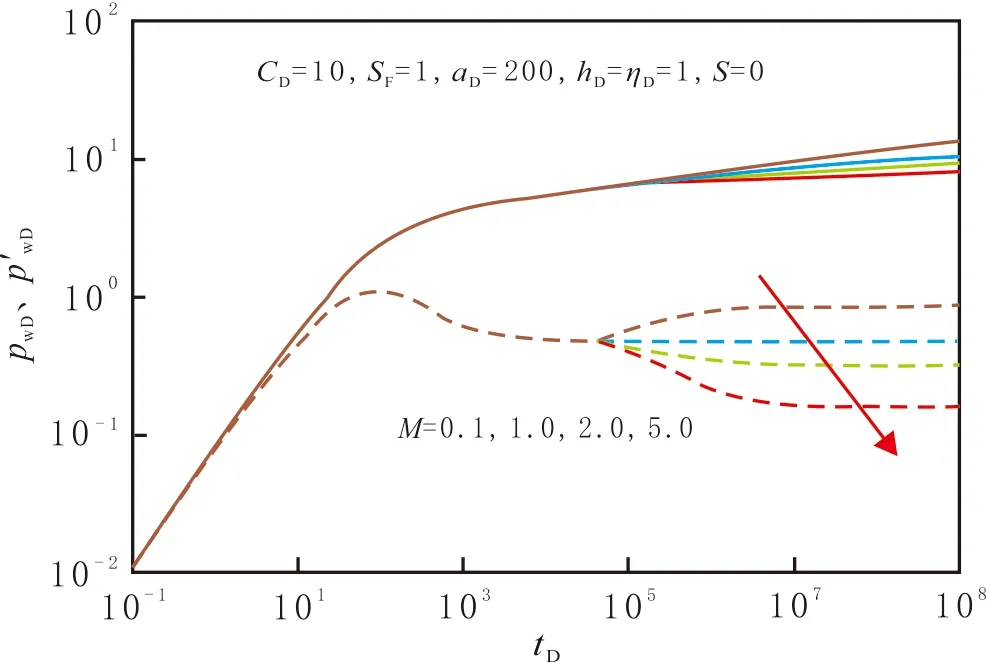
图5 流度比对压力响应特征曲线的影响Fig.5 Effects of M on the calculated dimensionless type curves

图6 厚度比对压力响应特征曲线的影响Fig.6 Effects of hD on the calculated dimensionless type curves

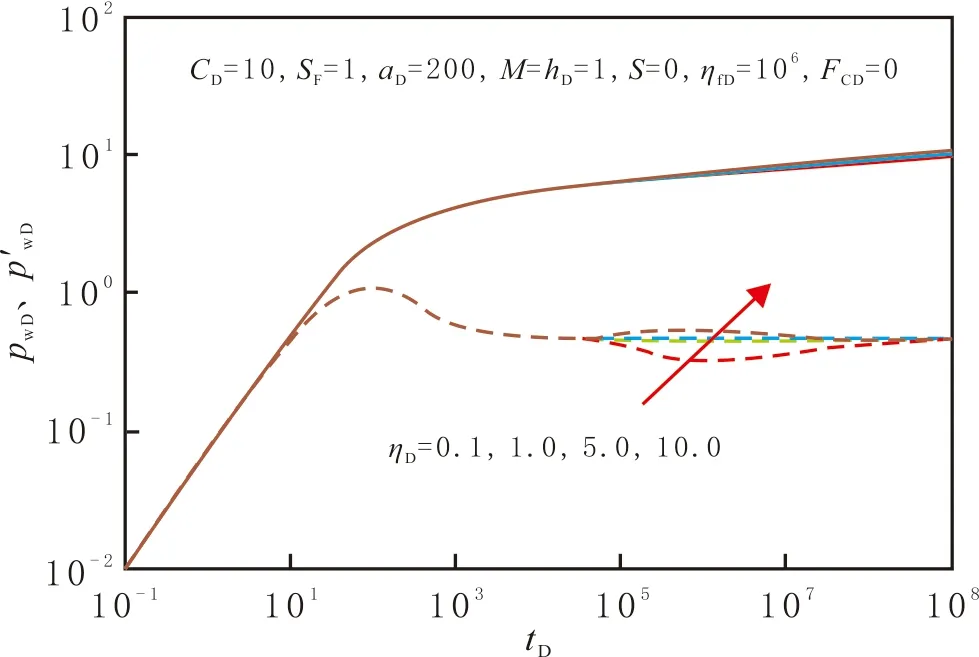
图7 导压系数比对压力响应特征曲线的影响Fig.7 Effects of ηD on the calculated dimensionless type curves

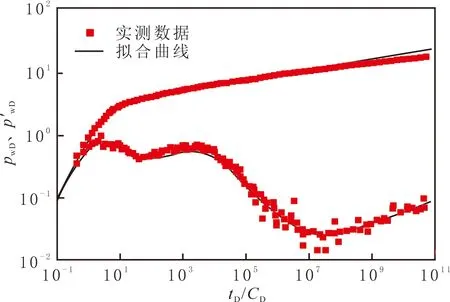
图8 某生产井实测数据与典型曲线拟合Fig.8 Double logarithmic fitting curve of production well

利用编制的实测离散压力点求导程序对压力差进行求导，观察压力和压力导数变化规律，结合生产井地区的地质研究，选用存在有限导流断层边界的无限大复合油藏模型进行拟合，拟合的双对数曲线见图8。拟合结果：井筒储集系数为3.14 m3/MPa，表皮因数为0.35，渗透率为12.67 ×10-3μm2，井到断层的距离为70.90 m，断层导流能力为1 000，断层界面表皮因数为80，断层导压系数为6.50×1011μm2/s。

根据试井解释结果判断断层连通性较好，对被断层隔开另一边的注水井采取加强注水措施，注水井对应的3口生产井产油量提高3.20%，试井解释结果符合油田实际情况，证实模型的正确性与实用性。

4 结论

(1)建立既考虑流体沿断层面流动，又考虑断层内部流体流动的有限导流断层试井解释模型，编程绘制并分析压力响应特征曲线。

(2)无因次断层导流能力越大，流体流动性越好，当其值足够大时，压力导数曲线表现为斜率为-1的特征，类似于定压边界的反应；界面表皮因数越大，流体流动的阻力越大，无因次压力及压力导数曲线位置越靠上，当其值足够大时，表现为封闭断层的特征；无因次断层导压系数主要影响压力导数曲线下降幅度，其值越小，压力导数曲线下降幅度越大。

(3)文中模型可用于研究双重介质油藏、条带状油藏等的试井解释及压力分布规律，对具有类似边界条件的油藏研究和应用具有借鉴意义。

参考文献(Reference):

[1] 程海生,杨风丽.油气田断层封闭性综述[J].特种油气藏,2008,15(1):6-12.

Cheng Haisheng, Yang Fengli. An overview of fault seal ability in oil and gas fields [J]. Special Oil and Gas Reservoirs, 2008,15(1):6-12.

[2] 吴明录,丁明才,姚军,等.分形离散裂缝数值试井解释模型[J].东北石油大学学报,2016,40(6):114-120.

Wu Minglu, Ding Mingcai, Yao Jun, et al. Numerical well-testing interpretation model based on fractal discrete fracture [J]. Journal of Northeast Petroleum University, 2016,40(6):114-120.

[3] 姜瑞忠,郜益华,孙召勃,等.基于点源解的偏心井试井典型曲线分析[J].东北石油大学学报,2016,40(4):80-87.

Jiang Ruizhong, Gao Yihua, Sun Zhaobo, et al. Eccentric well test type curve analysis based on point source solution [J]. Journal of Northeast Petroleum University, 2016,40(4):80-87.

[4] 王盛波.海拉尔盆地碎屑岩地层断裂带内部结构及断层封闭性[J].东北石油大学学报,2013,37(2):1-8.

Wang Shengbo. Internal structure of fault zone and fault lateral sealing in clastic rock layer of Hailaer basin [J]. Journal of Northeast Petroleum University, 2013,37(2):1-8.

[5] 苑保国,王晓东.封闭边界非均匀流量垂直裂缝井压力曲线特征及应用[J].特种油气藏,2008,15(6):48-51.

Yuan Baoguo, Wang Xiaodong. Characteristics and application of pressure curves of vertical fractured wells with closed boundary and nonhomogeneous flux [J]. Special Oil and Gas Reservoirs, 2008,15(6):48-51.

[6] Bixel H C. Effect of linear discontinuities on pressure build up and drawdown behavior [J]. Journal of Petroleum Technology, 1963,15(8):885-895.

[7] Yaxely L M. Effect of partially communicating fault on transient pressure behavior [J]. Society of Petroleum Engineers Formation Evaluation, 1987,2(4):590-598.

[8] Ambastha A K, McLeroy P G, Grader A S. Effect of a partially communicating fault in a composite reservoir on transient pressure testing [J]. Petroleum Engineers Formation Evaluation, 1989,4(2):210-218.

[9] Everdingen A F. The skin effect and its influence on the productivity capacity of a well [J]. Journal of Petroleum Technology, 1953,5(6):171-176.

[10] Hurst W. Establishment of the skin effect and its impediment to fluid flow in a wellbore [J]. Petroleum English, 1953,25(8):6-16.

[11] Boussila A K, Tiab D. Pressure behavior of well near a leaky boundary in heterogeneous reservoirs [J]. Production and Operations, 2003,18(10):158-164.

[12] Abbaszadeh M, Cinco-Ley H. Pressure-transient behavior in a reservoir with a finite-conductivity fault [J]. Society of Petroleum Engineers Formation Evaluation, 1995,10(1):26-32.

[13] 张望明,曾萍.存在局部连通断层的复合油藏不稳定试井分析及典型曲线拟合方法[J].石油勘探与开发,1992,19(2):69-76.

Zhang Wangming, Zeng Ping. Transient pressure testing analysis and type-curve matching in a composite reservoir with a partially communicating fault [J]. Petroleum Exploration and Development, 1992,19(2):69-76.

[14] 廖新维.考虑交接面附加阻力的复合油藏试井模型[J].大庆石油地质与开发,2001,20(5):30-31.

Liao Xinwei. Well test model of compound reservoir considering on additional resistance force on conjoining plate [J]. Petroleum Geology & Oilfield Development in Daqing, 2001,20(5):30-31.

[15] 刘启国,冯宇,董凤玲.受界面附加阻力影响的双重介质径向复合油藏试井解释模型研究[J].油气井测试,2005,14(3):11-13.

Liu Qiguo, Feng Yu, Dong Fengling. Study on testing interpretation model of dual medium and radial compound reservoir influenced by interface addition friction [J]. Well Testing, 2005,14(3):11-13.

[16] 罗建新,张烈辉,赖南君,等.两区线性复合油藏产能典型理论曲线分析[J].深圳大学学报:理工版,2011,28(5):384-388.

Luo Jianxin, Zhang Liehui, Lai Nanjun, et al. Typical deliverability curve analysis in bi-zonal linear composite reservoirs [J]. Journal of Shenzhen University: Science and Engineering, 2011,28(5):384-388.

[17] Stehfest H. Numerical inversion of laplace transforms [J]. Communications of Association for Computing Machinery, 1970,13(1):47-49.

[18] Everdingen A F. The application of the laplace transformation to flow problems in reservoirs [J]. American Institute of Mechanical Engineers, 1949,186(18):305-324.