基于高精度速度建模技术的孔隙压力预测方法建立
徐嘉亮,周东红,贺电波,边立恩,吕振宇(中海石油 天津分公司 渤海石油研究院,天津 300451)
地层异常压力与油气生成,运移以及存储密切相关。研究地层压力的变化特征可以发现油气运移的方向以及油气与岩性特征的相关性等基本规律。地层孔隙压力尤其是地层孔隙异常高压是影响钻井工程施工作业的主要因素之一。如果不能准确检测到孔隙压力的大小,将有可能导致钻进过程中井漏,井喷等诸多问题的产生。准确预测地层孔隙压力大小,是当前石油勘探生产中急需解决的技术难题。在钻前做好孔隙压力预测,对于发现油气藏,调配钻井液密度及井深结构,提高钻井成功率等都具有十分重要的意义。
人们在20世纪初就已经认识到孔隙异常高压是钻井事故的主要原因之一,但是当时还没有正式开展压力预测的相关工作。1965年Hottman和Johnson提出等效深度法,该方法利用已钻井得到的声波时差及电阻率建立正常压实曲线,但这种方法很难准确的预测地层压力[1]。Eaton在1975年提出了包含声波时差,页岩电阻率及DC指数三者的地层压力关系式,也就是大家普遍熟知的伊顿法。该方法需要参考大量的已钻井资料来确定经验公式中的Eaton指数,虽然这种方法有诸多的问题,但它仍然具有较高的实用价值,目前工业界也仍然在沿用这种方法[2]。20世纪80年代,Fillippone等通过对钻井,测井,地震资料等多方面资料的综合分析,提出了一种不依赖于正常压实速度,仅利用地层层速度预测孔隙压力系数的方法,也就是Fillippone公式法,该方法在国内外得到了广泛的应用[3-4]。在20世纪90年代,Foster注意到压力预测问题没有充分考虑异常压力的成因机制,因此提出一些经验公式,利用估算的有效应力来直接预测地层压力[5]。
在国内,地层压力预测技术也有相应的发展。刘震1990年在压力数据的测试中发现,地层压力与速度的关系并不是简单的线性内插关系,从而提出了改进后的Fillippone公式,从而提高了预测精度[6]。曾涛等把探井速度和断层封堵性应用到孔隙压力预测当中[7]。管志川等(2013)利用已钻井建立矩阵方程,从而对速度场进行有效的扰动更新[8]。桂俊川等(2015)对正常压实趋势线进行了有效区分,根据不同沙泥岩压实特点采用不同压实趋势线[9]。陈鑫等把地质认识与地震相结合,从而提出具有针对性的压力预测方法[10]。吴海生等应用钻井地层压力实测资料、录井资料和地震速度资料等,结合盆地地层沉积结构分析,对地层超压异常的横、纵向空间分布特征及其成因控制因素进行综合研究[11]。以上方法都需要层速度模型或者都围绕层速度建模展开研究,但很少有人针对孔隙异常高压地层低速的特点展开具有针对性的研究。本文从异常高压地层低速地震波场响应机理出发,创新提出炮域速度相干反演方法进行初始速度模型建立,角道集剩余曲率分析方法进行速度收敛,不规则网格层析方法进行局部修饰更新,该技术流程能够精确反演得到低速泥岩层段的速度,避免低速层射线多路径假象带来的误差,利用该技术流程得到的层速度进行孔隙压力预测精度更高。由实际数据应用证明本文提出的技术流程进行层速度建模及孔隙压力预测是有效可行的,该方法能够有效提高预测孔隙压力的精度,从而保证钻井施工的顺利展开。
1 算法建立
1.1 炮域波动方程反演相干方法
在工业界,地震资料处理人员常常利用DIX公式或DIX约束反演方法进行初始速度模型的建立。以上两种方法计算层速度效率高,但都基于水平层状介质的假设条件,并且是全层段的速度反演方法,不具有局部针对性[12]。
90年代中期,Landa等提出了一种CMP道集射线追踪速度相干反演的方法,该方法不以双曲近似或者叠前旅行时拾取为基础,而是通过射线追踪正演的方法得到旅行时曲线,在沿旅行时曲线的有效时窗内使叠前道集的相干达到极大,从而计算地层层速度的方法。所以这种方法完全由地震数据进行驱动,地震资料的信噪比及分辨率极大程度上决定了该方法的精度,这种方法也开辟了初始层速度场建模的全新思路。但是这种方法也存在很多缺陷,首先对于复杂的地质构造,例如高速火成岩或者低速泥岩,射线很难做到完全有效覆盖,从而导致正演数据缺失,这种缺失的正演数据与原始地震数据相关性较低,从而不能精确计算层速度。射线追踪正演算法对于高陡构造容易产生数值假频,这种假频信息参与到相干计算当中往往会带来不小的误差,甚至产生局部极值的假象。针对射线追踪正演方法的缺陷,本文提出利用波动方程高阶交错网格有限差分方法代替射线追踪正演方法,波动方程正演算法利用波场进行有效延拓,对于低速泥岩等复杂构造地层都有很好的适应性。
交错网格差分的主要思想是将空间的导数值在两个空间网格的中间进行计算,这样做的好处是在不增加计算量的情况下提高差分方程的精度。主体网格与交错网格两者相差半个网格间距。为了满足差分格式的需要,需要对差分方程的参数定义在主体网格和交错网格上[13]。
对于空间高阶差分格式,在交错网格技术中,变量的导数是在相应网格点之间的半程上计算的。为此,采用下式计算一阶空间导数:
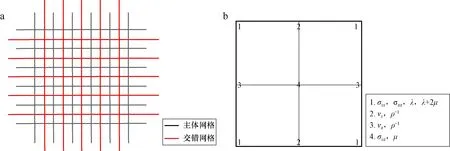
图1 交错网格划分Fig.1 Staggered grid divisiona.交错网格,b.单元网格参数定义
(1)
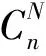
对各向同性介质速度应力弹性波方程给出10阶空间差分精度的差分格式,相应的差分网格如图1所示。最终交错网格有限差分格式为:
有限差分法是用有限的离散值来代替连续的介质,这样必然会产生数值频散问题。减小这种误差最有效的方法就是减小空间网格,从而增加空间采样率。但是这样做的弊端是成倍增加了计算时间。利用以上提出的高阶交错网格有限差分方法既可以在空间上减小计算网格,从而增加了采样率,而且还有效缩短了计算时间,提高了计算效率。
波动方程相干反演方法首先对各层进行速度扫描,扫描出一系列各个层位及构造体的虚拟层速度,然后利用高阶交错网格有限差分方法正演得到炮集记录,最后利用模型炮集及实际数据炮集做相干分析,相干度最高的炮集对应地层的虚拟层速度即为该层初始层速度,该方法具有很强的局部针对性,对于泥岩欠压实引起的低速泥岩地层初始速度反演更为精确,虽然该方法计算量较大,但是其初始速度建模精度较高,对于一些具有较大超压风险且易造成钻井施工事故的工区是非常有必要的。
1.2 角度域共成像点道集层析成像方法
在常规共反射点道集中,构建道集的参数包括入射射线参数ps及出射射线参数pr,偏移距r以及射线走时t。当地下存在低速体时(图2),实线与虚线的射线走时相等t1=t2,且射线参数相等,既ps1+pr1=ps2+pr2,从而形成射线多路径的假象,这种假象给层速度求取带来很大的误差[14]。
与偏移距域道集不同,角道集是波场延拓到地下目标区域之后,从部分成像数据中按深度域的入射角排列生成的。如果给定反射倾角,反射点位置及入射角度,那么射线路径就可以唯一确定(图3)。因此,从深度域成像数据中输出的角道集不会受低速异常体的影响,从而提高层速度场求取精度。

图2 共偏移距多路径假象Fig.2 Multipath illusion of common offset
本文以图4所示的观测系统为例进行公式推导。Z0为真实反射界面的深度,m;ZW是实际的聚焦深度,m;V0为真实目标层速度,m/s;h0为地表偏移距,m;t0表示零偏移距旅行时,s;h为波场向下延拓的局部偏移距,m。当速度正确时,时距曲线关系式为:
(7)
当利用正常压实速度时,也就是局部偏移速度大于地层速度时,由上式可推断其时距曲线关系式为:
(8)
设偏移速度与真实速度误差为ΔV。结合(7)式和(8)式,可得剩余速度与偏移深度之间的关系式(9):
(9)
因为地表偏移距不随偏移深度变化,所以式(9)两边对h0求导,等式依然成立,得到地表偏移距与局部偏移距的关系式(10):
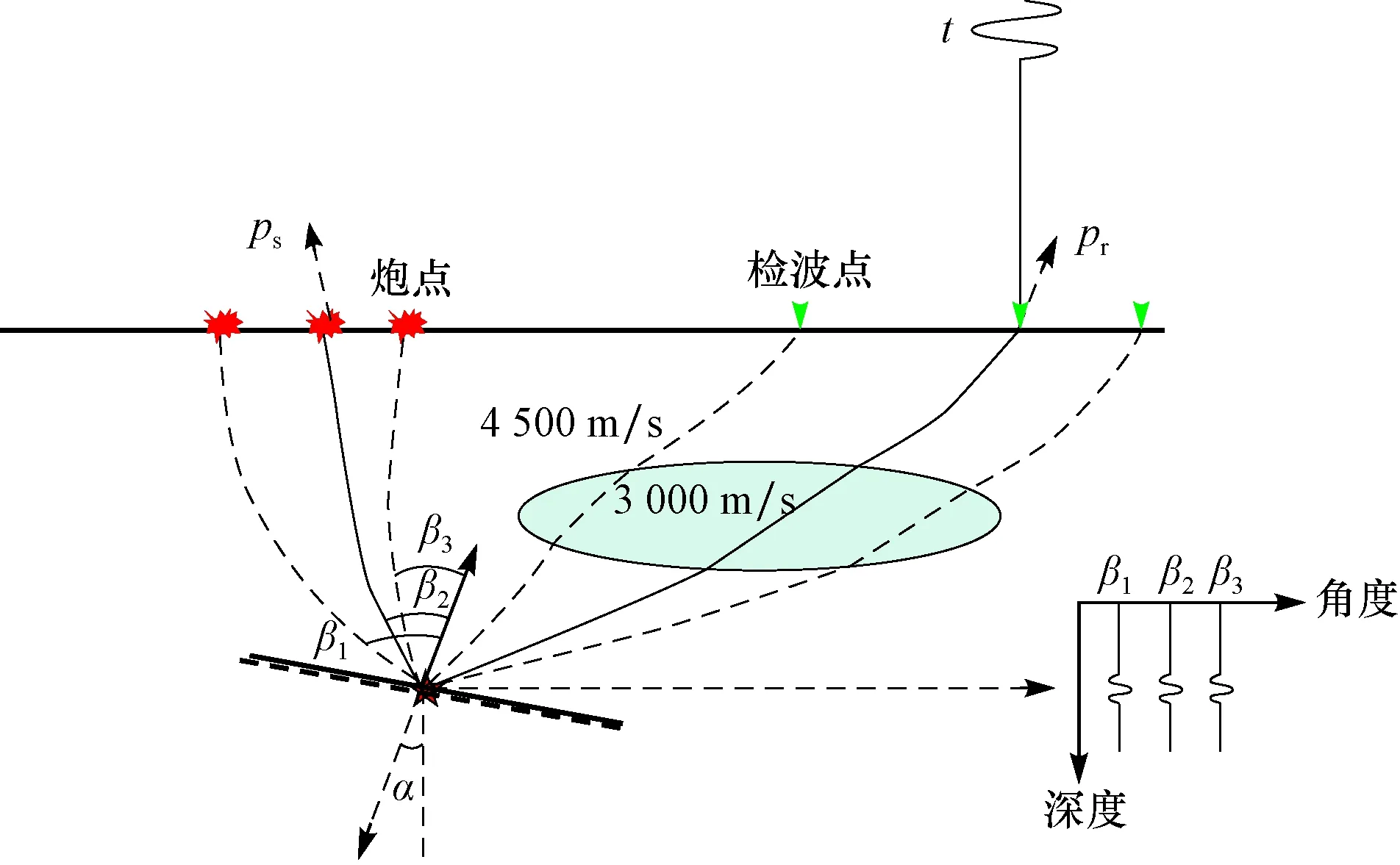
图3 角度域成像对多路径假象问题的适应性Fig.3 Adaptability of the angle domain imaging to multipath illusion
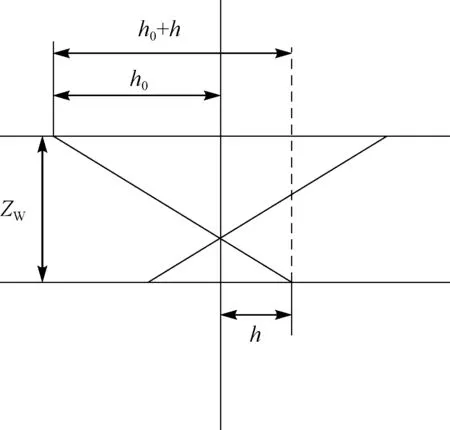
图4 角度域局部观测系统Fig.4 Local observation system in angle domain
(10)
把方程(10)代入方程(9)可以消除地表偏移距,得到:
引入角度的概念,单程波成像过程中抽取角道集的倾斜叠加公式由Sava(2003)提出:
(12)
把抽取角道集的倾斜叠加公式变形并且代入式(12)可得:
(13)
公式(13)两边对h求导,并反代入式(12)整理之后得:
公式(14)是以剩余曲率为自变量,剩余速度为目标函数建立的,利用公式(14)就可以对初始层速度模型进行层析迭代。
角道集层析速度建模方法有效避免了偏移距域道集射线多路径假象,解决了泥岩欠压实低速地层射线多路径假象导致的孔隙压力预测误差问题,提高了计算孔隙压力系数的精度。
1.3 基于层位约束的网格层析方法
网格层析速度建模方法近几年受到学者的广泛关注,该方法实现了小尺度范围内更新层速度场信息,适用于高陡倾角及特殊地质体精确层速度求取。但是常规网格层析利用规则矩形网格对地下构造进行剖分,利用离散的网格点代替地下连续的介质,但是该方法没有充分考虑地层的分布规律。对于复杂构造地层,均匀网格分布不能完全表征地层分布特点,从而降低层速度模型反演的精度和效率(图5a)。
本文提出一种基于层位约束的网格层析速度建模方法,该方法利用层位信息控制网格分布,在对地下地层进行均匀网格剖分的同时对有层位及特殊地质体的地层进行网格剖分(图5b)。在有反射层位的地层加密网格,从而实现真正小尺度的精细层速度修饰(图6)。
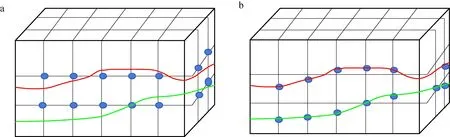
图5 网格层析Fig.5 Grid tomographya.均匀网格;b.基于层位约束的网格
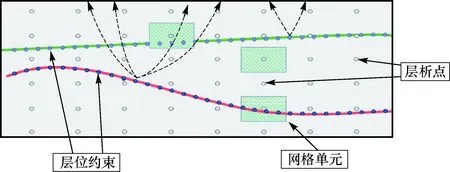
图6 层位约束网格层析网格分布Fig.6 Grid distribution in horizon-constrained grid tomography
该方法以拾取道集剩余延迟量为自变量,层速度为目标函数,利用地层倾角,方位角,地层连续性的信息对网格剖分进行控制,如公式(15)所示。
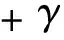
(15)

2 实际数据应用
利用本文提出的层速度建模新流程对渤海M区块进行实际应用,该区低速泥岩层广泛发育,已钻井共测有两个测压点,压力系数分别为:1.31(2 803 m), 1.4°(3 109 m)。
分别利用常规偏移距层析成像方法及本文提出的速度建模技术流程进行层速度场建模,层速度模型及抽取的围井速度曲线与测井声波速度曲线比较如图7和图8所示。
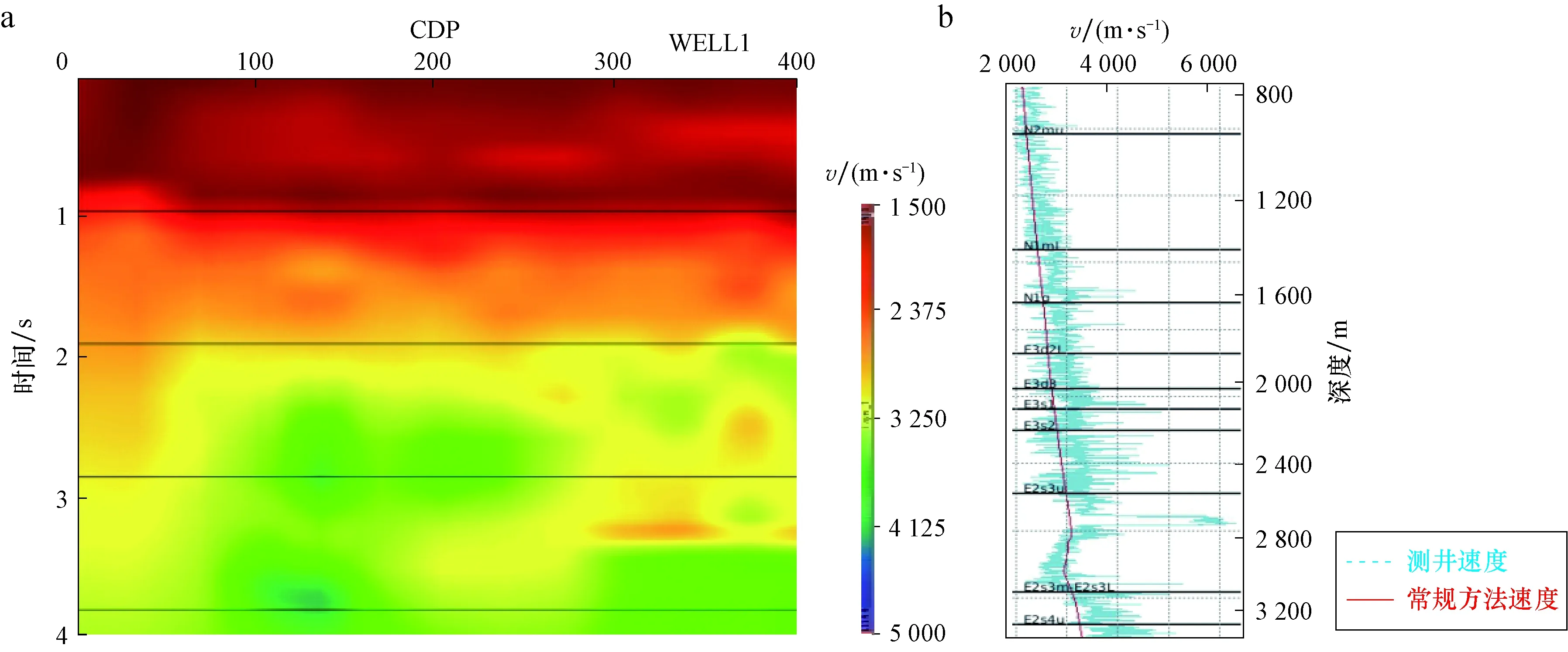
图7 常规方法速度建模Fig.7 Conventional method of velocity modelinga.常规方法速度模型;b.井旁速度曲线与声波测井曲线对比
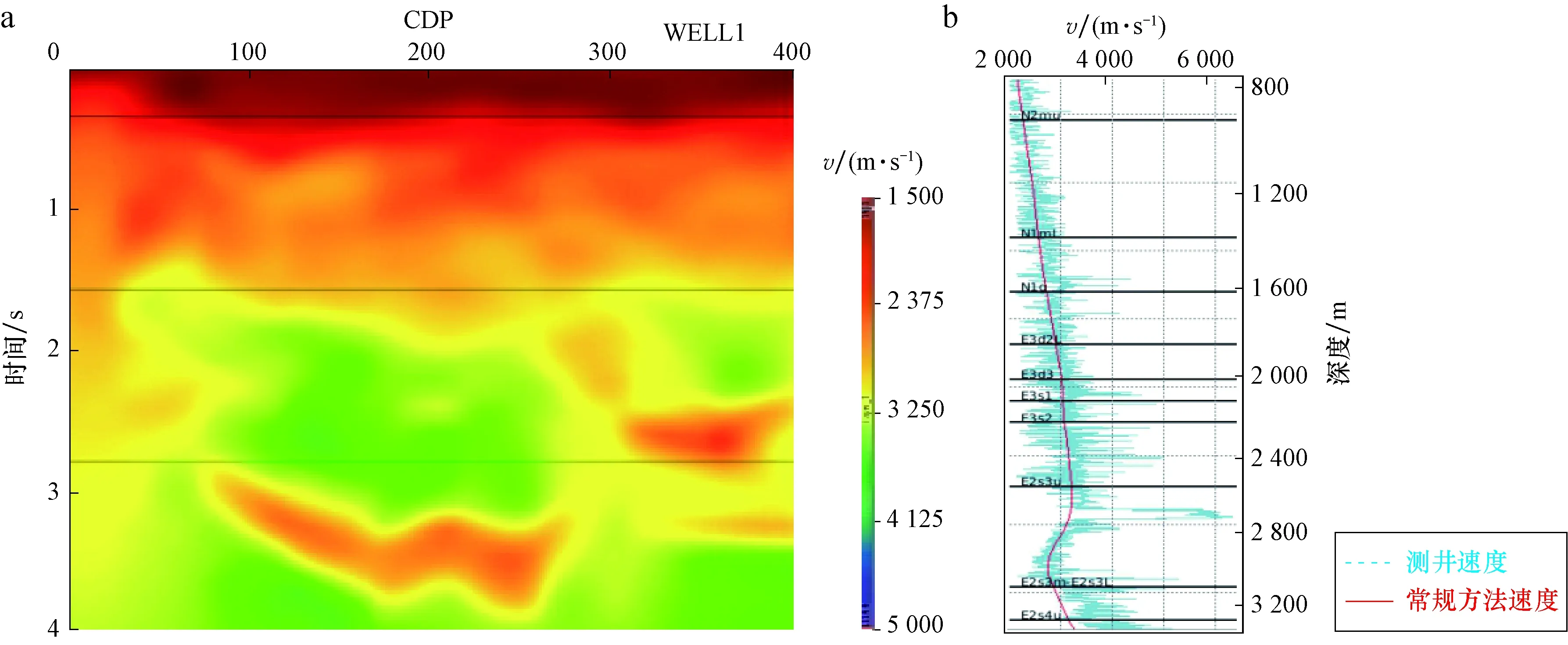
图8 新方法速度建模Fig.8 New method of velocity modelinga.新方法速度模型;b.井旁速度曲线与声波测井曲线对比
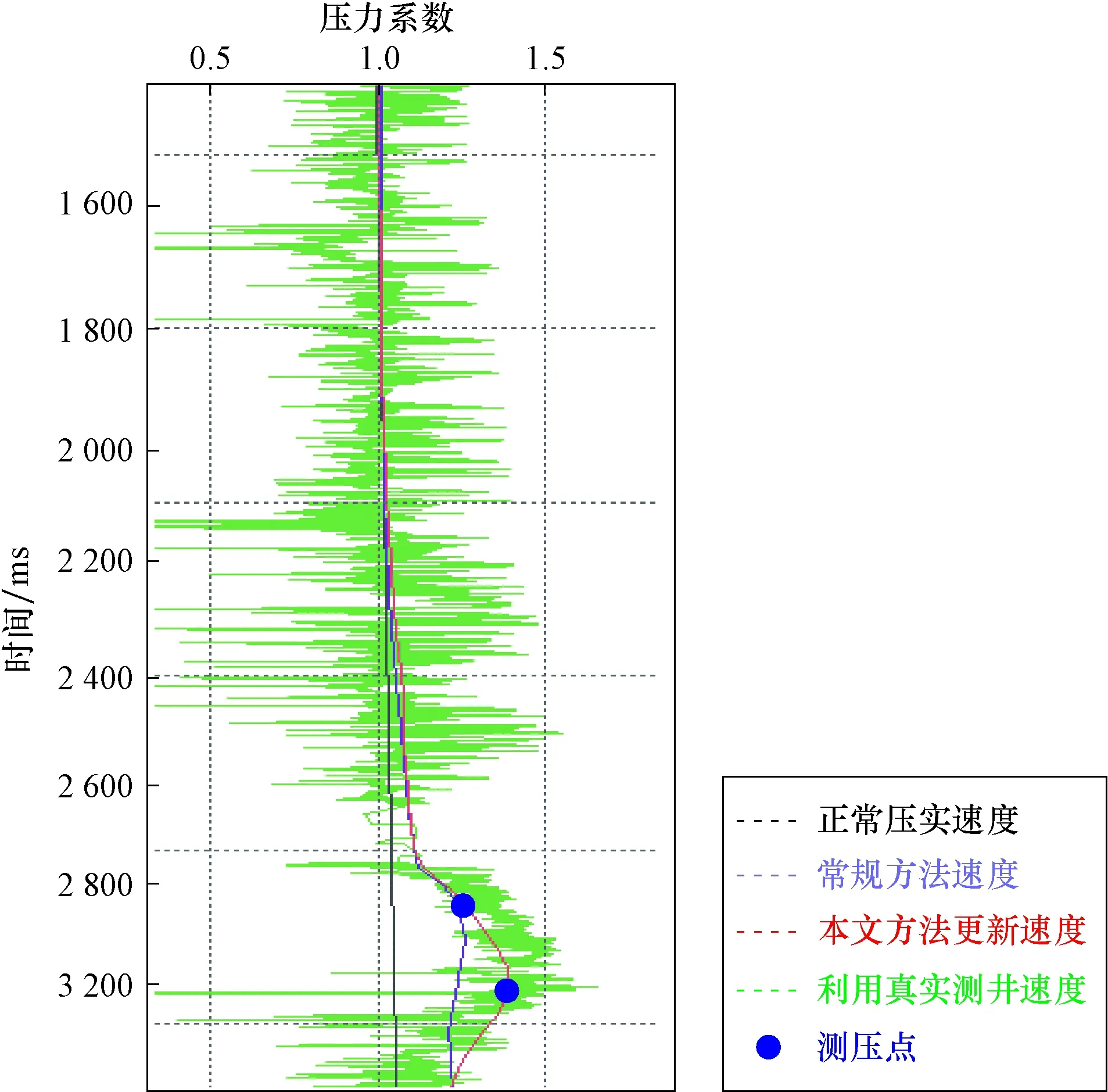
图9 孔隙压力系数比较Fig.9 Comparison of pore pressure coefficients calculated with different methods
由抽取的围井速度曲线与实际声波测井曲线比较中可看出,常规层析成像方法得到的层速度与真实层速度有不小的偏差,低速泥岩层段速度误差较大,利用该层速度模型进行孔隙压力系数计算必然会产生较大误差。利用本文提出的技术流程进行层速度场建模抽取的围井速度曲线与实际声波测井曲线吻合度较高,速度建模精度得到显著提高,利用该层速度模型进行孔隙压力预测精度可显著提高(图9)。
利用常规层析方法与本文提出的技术方法速度建模得到的层速度模型进行孔隙压力系数计算,常规方法计算得到的压力系数与实测压力系数值有较大偏差,利用本文方法得到的层速度计算的孔隙压力系数与实测压力系数吻合度非常高,从而再次说明本文提出的方法适用性强且精度高,应在孔隙压力预测工作中广泛推广。
3 结论
利用Eaton公式计算孔隙压力系数需要结合深度域层速度模型,在工业界深度域层速度模型普遍由偏移距域道集层析成像得到。常规偏移距域道集存在射线多路径假象误差,这种误差给层析速度建模带来不小的误差,从而影响计算孔隙压力系数精度。本文根据孔隙异常高压地层低速的特点,创新提出利用炮域速度相干反演方法进行初始速度模型建立,利用角道集剩余曲率分析方法进行速度收敛,利用基于层位约束的网格层析方法进行局部更新的三步组合技术流程,该技术流程有效提高了欠压实低速泥岩速度求取的精度。由实际数据应用证明本文提出的技术流程进行层速度建模及孔隙压力预测是有效可行的,该方法能够有效提高预测孔隙压力系数的精度,从而保证钻井施工安全,为勘探开发阶段油气预测提供更为有利的依据及保障。
参 考 文 献
[1] Hottmann C E,Johnson R K.Estimation of formation pressures from log-deriverd shale properties[J].Journal of Petroleum Technology,1965,17(6):717-722.
[2] Eaton B A.Graphical method predicts geopressures worldwide[J].World Oil,1972,51-56.
[3] Fillippone W R.On the prediction of abnormally pressured sedimentary rocks from seismic data[C]∥Offshore Technology Conference.Houston:11thAnnual OTC,1979:2667-2676.
[4] Fillippone W R.Estimation of formation parameters and the prediction of overpressures from seismic data[C]∥Annual International Meeting.America:SEG,1982:502-503.
[5] Foster J B,Whalen H E.Estimation of formation pressures from electrical surveys-Offshore Louisiana[J].Journal of Petroleum Technology,1987,18(2):165-171.
[6] 刘震,张厚福.辽西凹陷北洼下第三系异常地层压力分析[J].石油学报,1993,14(1):14-24.
Liu Zhen,Zhang Houfu.An analysis of abnormal formation pressures of paleogene in the north sag of liaoxi depression[J].Acta Petrolei Sinica,1993,14(1):14-24.
[7] 曾涛,徐宏节.地震层速度在断层封堵性研究中的应用[J].石油与天然气地质,2000,21(2):161-163.
Zeng Tao,Xu Hongjie.Application of Seismic interval Velocity in the study of fault plugging[J].Oil & Gas Geology,2000,21(2):161-163.
[8] 管志川,魏凯.利用已钻井资料构建区域地层压力剖面的方法[J].中国石油大学学报,2013,37(5):71-76.
Guan Zhichuan,Wei Kai.Method for constructing regional formation pressure profile by using drilled data[J].Journal of China University of Petroleum,2013,37(5):71-76.
[9] 桂俊川,陈颖杰.基于两种压实趋势线计算地层孔隙压力的新方法[J].国外测井技术,2015,205(1):24-31.
Gui Junchuan,Chen Yingjie.A new method to calculate formation pore pressure of two kinds of compaction trend line based on[J].Foreign Logging Technology,2015,205(1):24-31.
[10] 陈鑫,魏小东,李艳静,等.基于地震资料的探井钻前孔隙压力预测[J].石油与天然气地质,2015,36(6):1039-1046.
Chen Xin,Wei Xiaodong,Li Yanjing.Pre-drilling pore pressure prediction based on seismic data for exploratory well:Oilfield A in Iraq[J].Oil & Gas Geology,2015,36(6):1039-1046.
[11] 吴海生,郑孟林,何文军,等.准格尔盆地腹部地层压力异常特征与控制因素[J].石油与天然气地质,2017,38(6):1136-1145.
Wu Haishen,Zheng Menglin,He Wenjun.Formation pressure anomalies and controlling factors in central Juggar Basin[J].Oil & Gas Geology,2017,38(6):1136-1145.
[12] 梁瑶,王真理.利用双路径积分算法进行高密度偏移速度建模[J],石油地球物理勘探,2016,51(1):142-164.
Liang Yao,Wang Zhenli.High-density migration velocity model building using double path integral[J],Oil Geophysical Prospecting,2016,51(1):142-164.
[13] 董良国,马在田,曹景忠,等.一阶弹性波方程交错网格高阶差分解法[J].地球物理学报,2000,43(3):37-41.
Dong Liangguo,Ma Zaitian.One order elastic wave equation staggered grid high-order difference method[J].Chinese Journal of Geophysical,2000,43(3):37-41.
[14] 徐嘉亮,常旭,王一博,等.角度域剩余深度对剩余速度的敏感性分析[J].地球物理学报,2015,58(8):2928-2934.
Xu Jialiang,Chang Xu,Wang Yibo.Sensitivity analysis of angle domain residual depth on residual velocity[J].Chinese Journal of Geophysical,2015,58(8):2928-2934.
[15] 张国栋,马光克.速度体高精度建模法在深水M气田时深转换中的应用[J].地球物理学进展,2016,31(5):2246-2254.
Zhang Guodong,Ma Guangke.Application of high precision velocity modeling methods for time-depth conversion in deepwater M gas field[J].Progress in Geophysics,2016,31(5):2246-2254.

