计及计划检修和强迫停运的变压器备用规划

王 曼 王永华



计及计划检修和强迫停运的变压器备用规划

王 曼 王永华

（国网重庆市电力公司江北供电分公司，重庆 400044）

设备计划检修可改善设备的健康状态，有利于提高设备和系统的可靠性，然而变电站变压器检修可能造成停电损失。本文综合考虑计划检修和强迫停运，采用序贯蒙特卡洛方法计算变压器组可靠性指标，以备用变压器的种类和数量为决策变量，以变压器组总费用最小为目标，建立变压器组备用规划模型，给出变压器最优备用配置方案的枚举方法。算例对两个不同的区域分别进行变压器备用规划，结果表明：配置MS可以提高系统的可靠性，在本文给定的可靠性和经济性参数下，当仅针对计划检修导致的停电损失时，是否需要配置MS的决策受区域变电站的构成类型影响；综合考虑计划检修和强迫停运下，经济性最优配置数量受区域变电站的构成类型影响。

变压器备用；可靠性评估；计划检修；强迫停运；蒙特卡洛模拟

对输配电设备进行计划检修是电网必不可少的一项重要工作，定期对设备计划检修可改善设备的健康状态，有利于提高设备和系统的可靠性。然而在分析高压配网变电站变压器的备用配置时，不应忽略因变电站变压器检修造成的停电损失。本文将把变压器的计划检修、一类故障、二类故障和备用模式等统一纳入变压器组可靠性评估和备用规划过程。目前，已有较多的文献探讨了考虑备用的输配电设备的可靠性评估，此类文献主要体现在高压直流系统阀和换流变的备用，配电变压器备用等领域。

文献[1-3]基于马尔科夫过程，建立考虑备用的阀组和换流变压器组的状态空间图，表征了备用元件存在时设备组的状态转移关系。文献[4]考虑到了换流变压器的主设备和附属设备的不同的失效模式和对应的备用模式，并根据失效模式划分子系统，建立每个子系统的状态空间图。文献[5]使用备用变压器的安装时间直接代替变压器的修复时间。该方法简单清晰，但是难以考虑多种备用设备的替换过程，且不能准确计算系统的频率指标。

鉴于上述问题，本文综合考虑计划检修和强迫停运，采用序贯蒙特卡洛方法[6-9]计算变压器组可靠性指标，以备用变压器的种类和数量为决策变量，以变压器组总费用最小为目标，建立变压器组备用规划模型，给出变压器最优备用配置方案的枚举方法。

1 考虑计划检修和强迫停运的变压器组备用可靠性评估

1.1 考虑计划检修的变压器元件可靠性模型

根据《输变电设备检修导则》[10]，结合实际工程，综合考虑变压器在运行中出现的故障类型，建立变压器全状态模型，该模型为变压器在运行过程中可能出现的全部状态，如图1所示。

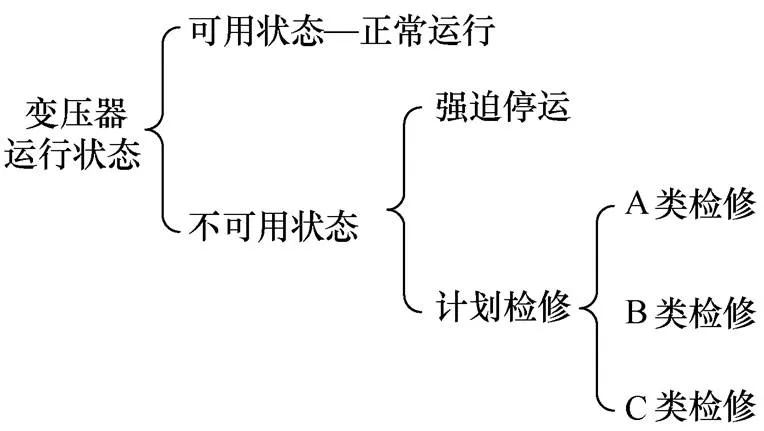
图1 变压器全态模型

计划检修分为三类：A类检修是指设备需要停电进行的整体检查、维修、试验工作；B类检修是指设备需要停电进行的局部检查、维修、更换、试验工作；C类检修是指设备不需要停电进行的检查、维修、更换、试验工作[11]。

1.2 序贯蒙特卡洛的可靠性评估方法

变压器的备用过程包括变压器发生故障、备用变压器的安装和替换、修复完成后备用设备的闲置等，该运行过程为时序过程。由于全年负荷的变化，不同时段的故障导致的失负荷也不同，因此，应用时序蒙特卡洛模拟，可获得较为准确的可靠性评估结果。可靠性评估的蒙特卡洛方法的基本理论是，基于元件运行与停运的概率模型，产生随机数进行随机抽样，模拟系统的失效事件，形成系统的时序状态转移过程，从而计算得到系统的可靠性指标。

本文考虑变压器计划检修的过程以及备用设备安装的过程，由于存在计划检修决策和移动变电站（MS）的投运决策两种人工干预的因素，变压器的状态转移过程并非完全随机的，因此，应用蒙特卡洛模拟法计算考虑备用的变压器组可靠性时，需要按照预先安排的规则对蒙特卡洛模拟过程进行修正。

1）系统参数初始化。包括各变电站的变压器容量、台数和可转带负荷容量、各变电站季度的日负荷曲线、计划检修安排的月份、随机故障和计划检修相关的可靠性参数；初始时所有元件处于运行 状态。

2）生成每个元件故障前工作时间，并判断该元件的停运类型（一类故障、二类故障、计划检修）。

3）若该元件的下一个模拟状态为计划检修：首先根据检修时段负载率和负荷转供情况，判断检修是否发生停电；若要停电，则调用移动变电站（MS）进行供电；否则，直接安排检修。在计划检修时刻，若配置的MS处于不可用状态（即MS正在用于其余某个变电站的故障备用），则该元件的检修时刻需要被推迟，直到MS完成其他任务重新可用时才开始检修，并记录该次计划检修的停电持续时间和失负荷功率。

4）若元件发生一类故障，先安装MS进行替换，再进行故障修复，此时停运持续时间为MS的安装时间；当元件发生二类故障时，在RT和MS同时存在的条件下，先安装MS，停运时间为MS的安装时间，其后安装常规备用变压器（RT），并将MS替下，发生故障的变压器则被托运至工厂进行修复。根据故障发生时段的负载率和转供情况，记录该次故障导致的失负荷量。

5）根据各变电站的状态转移曲线，计算各变电站的可靠性指标。

概率、频率和持续时间指标的计算式如式（1）—式（3）所示：

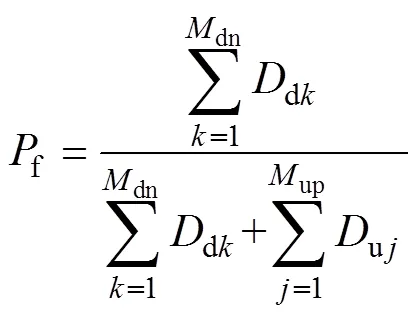
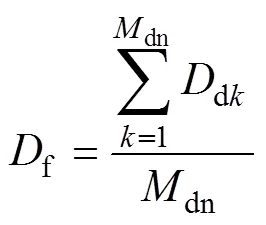
式中，f、f和f分别为失效概率、频率和平均持续时间；dk为第个停运状态的持续时间；uj为第个运行状态的持续时间；dn和up分别为在模拟时间跨度内变电站失效和运行状态出现的次数[12]。

2 变压器组备用的规划模型

110kV变电站中，无论是因变压器强迫停运还是计划检修，其停运都可能会导致负荷停电且修复时间较长[13]。因此，通过配置备用变压器可减少停电时间，提高供电可靠性。

本文将以系统总费用最小为目标，综合考虑变压器的随机故障和计划检修带来的停电损失，建立备用设备规划模型，以确定每种类型备用变压器的最优数量。

2.1 变压器组备用规划模型的目标函数

本文以变压器组的备用种类和数量为决策变量，以备用设备投资费用、备用设备运维费用，变压器组的强迫停运停电损失，以及计划检修停电损失之和最小为目标，建立备用规划模型，目标函数为

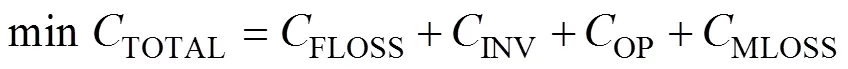
式中，TOTAL表示系统总费用；FLOSS为变压器强迫故障造成的停电损失费用；INV为备用设备投资费用；OP为备用设备运维费用；MLOSS为计划检修造成的停电损失费用。

变压器组强迫故障停电损失费用的计算式如下：

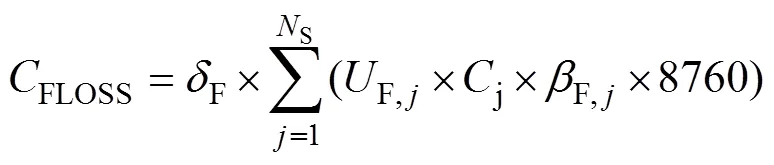
式中，F为强迫故障的单位停电损失；F, j是因第座变电站的变压器强迫故障造成的该变电站的变压器组不可用率，该变量衡量了变压器组能够正常运行的变电容量的期望。需要指出的是，变压器组为该变电站包含的所有主变压器组成的集合。C是该变电站额定容量；F, j是第座变电站变压器强迫故障时失负荷功率与该变电站容量的比率，该参数与变电站容量、负载率和联络线建设情况有关。F, j可由下式估算，即

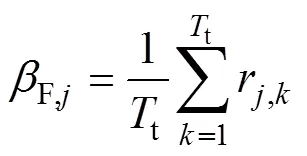
备用设备投资成本的等年值的计算式如下[14]：

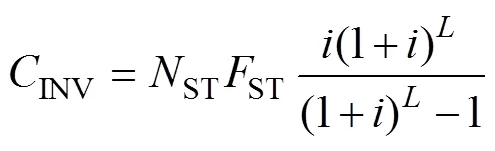
式中，ST为备用设备的台数；ST为单台备用设备购置价格；为折现率；为备用设备的使用寿命。

备用设备的安装替换任务需要消耗维修资源，备用运行过程中会产生损耗，这些过程造成的费用统称为设备运维费用。通常，运维费用可按投资费用的一定比例考虑，即

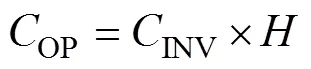
式中，表示备用设备运维成本占投资成本的比例系数。

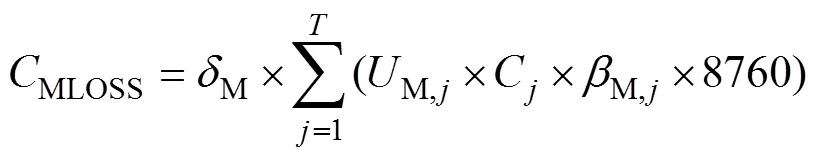
式中，MLOSS为计划检修导致的年停电损失费用；M为变电站计划停电的单位停电损失；M, j为因第座变电站计划检修造成的该变电站的变压器组不可用率；C为单座变电站额定容量；M, j为第座变电站变压器计划检修时失负荷功率与该变电站容量的比率，M, j与该变电站容量、检修时段的负载率和联络线建设情况有关。

2.2 变压器组备用规划模型的约束条件

结合工程实际，变压器组备用规划模型需要考虑的约束条件如下。

1）备用设备数量约束

变压器组中的备用台数需满足如下约束，即

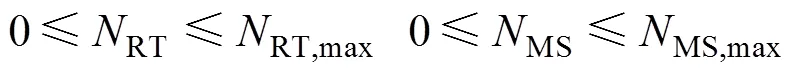
2）变压器组可靠性约束

对于给定的变压器组系统，如果系统规划者对变压器组的可靠性有要求，可以设置可靠性约束，即

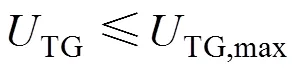
3）备用设备容量约束

备用变压器的容量应不小于所有可以配置备用的单台变压器所带峰荷的最大值，即

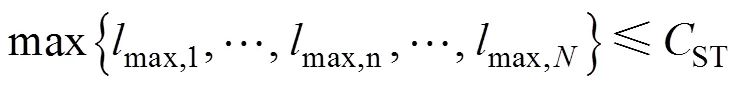
式中，max,n为变压器的峰值负荷；ST为备用设备的额定容量。

3 变压器组备用规划模型的求解算法

本文以电力变压器备用的类型和数量为决策变量，建立经济性最优的规划模型。利用序贯蒙特卡洛方法计算所需的可靠性和经济性指标，具体的算法如下。

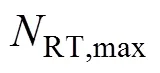
步骤2：生成随机数，得到每台变压器的初始正常运行持续时间。

步骤3：比较所有变压器状态转移时刻点，选定最早发生状态转移的变压器。

步骤4：判断该变压器的状态转移类型，若为强迫停运，根据可用备用类型生成对应的修复时间；根据计划检修率，每间隔若干年，在元件时序状态转移曲线上安排计划检修停运，并生成计划检修持续时间。

步骤5：按以下情形进行分析：

1）当故障类型为一类故障，若存在可用MS，则安装MS，停运时间为MS安装时间，否则，停运时间为一类故障的修复时间。

2）当故障类型为二类故障，故障变压器不能在变电站内修复，需要运回工厂进行维修。若RT和MS同时存在，先安装MS恢复供电，再开始安装RT以替换故障的变压器，停运时间为MS安装时间；若此时只有可用RT而无MS，则直接使用RT替换，停运时间是RT安装时间；若此时均无可用的RT和MS，停运时间是二类故障的修复时间。

3）计划检修安排在每年的固定的时段。若对某台变压器的检修会造成失负荷且在检修时段没有可用的MS，则该变压器的检修时刻需要被推迟，直到系统中MS处于可用状态。

步骤6：判定是否到达预先设定的模拟年限，若已到达，则停止模拟。若未到达，则返回步骤3。

步骤7：计算各变电站和变压器组的可靠性相关指标。

步骤8：根据式（4）至式（9），计算该备用方案的各项费用，进而得到系统总费用TOTAL。

步骤9：判断是否满足常规备用变压器RT,max上限，若满足，则进行下一步；否则，令RT=RT+1并转入步骤2。

步骤10：判断是否满足移动变电站MS,max上限，若满足，则计算结束并输出各个方案下的可靠性指标和费用计算结果；否则，令RT=0，MS=MS+1并转入步骤2。

4 算例分析

将本文的备用规划模型应用到A、B两个不同区域的电网，其中两个区域均包含40座110kV变电站。A区域变电站规划和建设比较坚强，大部分变电站采用双主变配置，B区域变电站建设略微薄弱，一部分变电站采用单主变配置，两地区变电站类型的比例见表1。备用设备使用寿命为30年，贴现率为7%[15]，强迫停运单位停电损失费用为49元/ kW·h[16]，计划检修单位停电损失费用按照单位电量的产值考虑，为13元/kW·h[17]。备用设备运维费用占投资费用的比例系数为1.8%[18]。各变电站峰值负载率统一考虑为0.75，对于含两台主变的变电站，强迫故障的失负荷比率dou为0.208%，而仅含一台主变的变电站的失负荷比率sin为13.7%。变压器计划检修率为0.2次/年[19]，单次检修时间为24h。计划检修通常安排在负荷较低的时段，本文中计划检修时变电站的日峰值负载率统一考虑为0.58[14]。具体所需要的可靠性及经济性参数见表2[20]。

表1 两地区110kV的不同类型变电站的数目

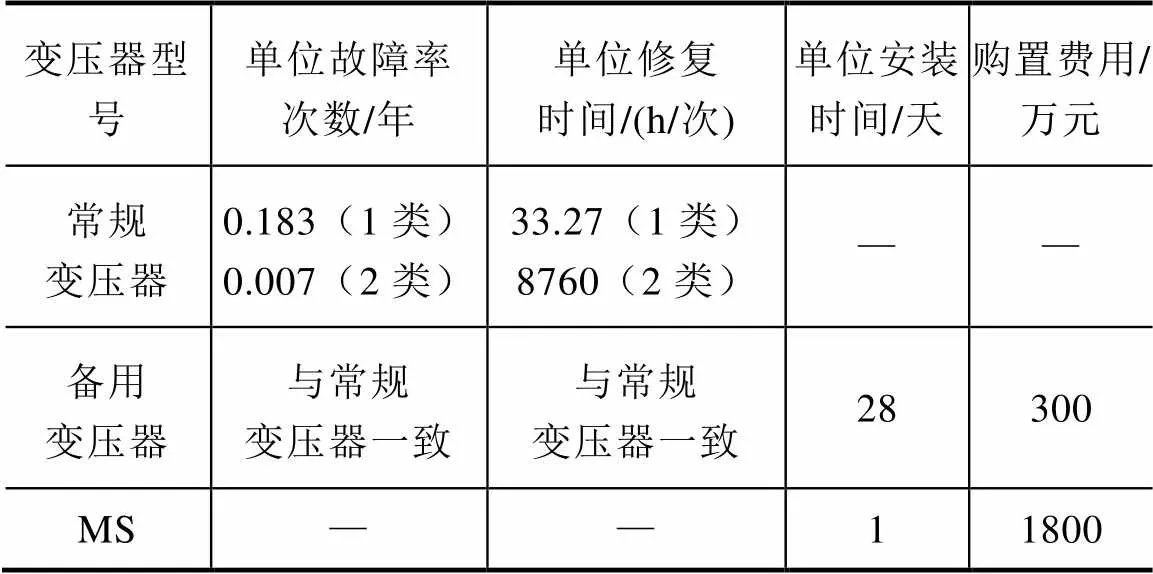
表2 110kV变压器相关的可靠性及经济性参数

4.1 可靠性计算结果

在考虑计划检修和强迫停运（一类故障、二类故障）的多种情况下，不同类型、不同数量的备用设备对变压器组的可靠性的影响的计算结果如下。

1）强迫停运的相关可靠性指标

由表3和表4可以得出，区域A和区域B系统出现强迫故障时，随着备用数量的增加，变压器组的不可用率逐渐降低。需要指出的是，表中的变压器组指系统所有的主变压器组成的集合，与单个变电站的变压器组的范畴不同。在RT数量一定的情况下，MS数量由0台增加到1台时，变压器不可用率降低较为明显，可靠性显著提高。但是MS数量从2台增加至3台时，变压器组不可用率几乎不再发生变化。

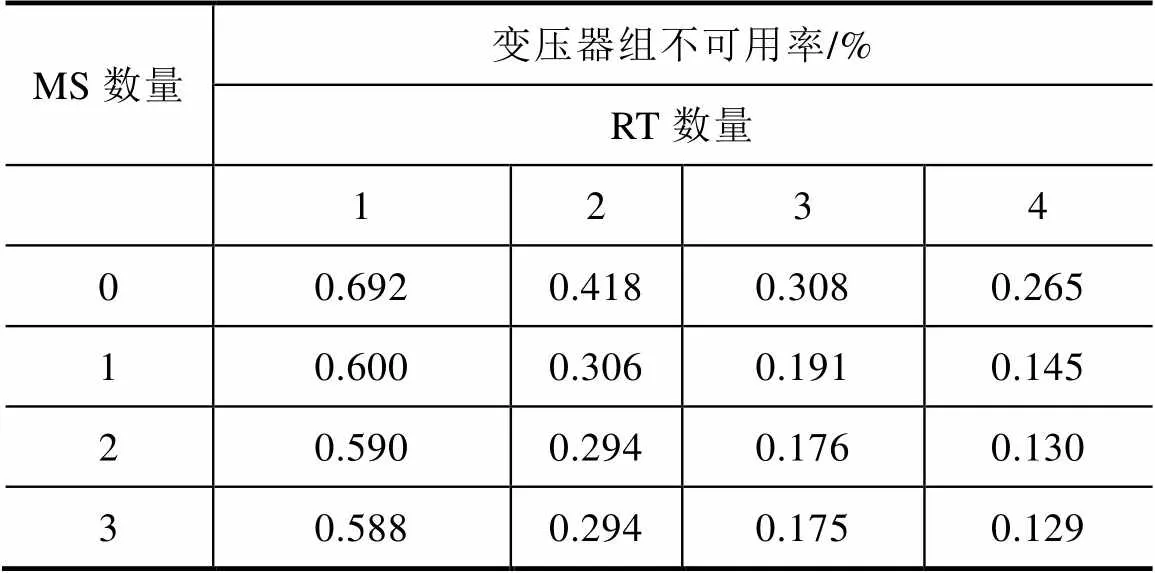
表3 强迫停运造成的变压器组可靠性指标-A区域

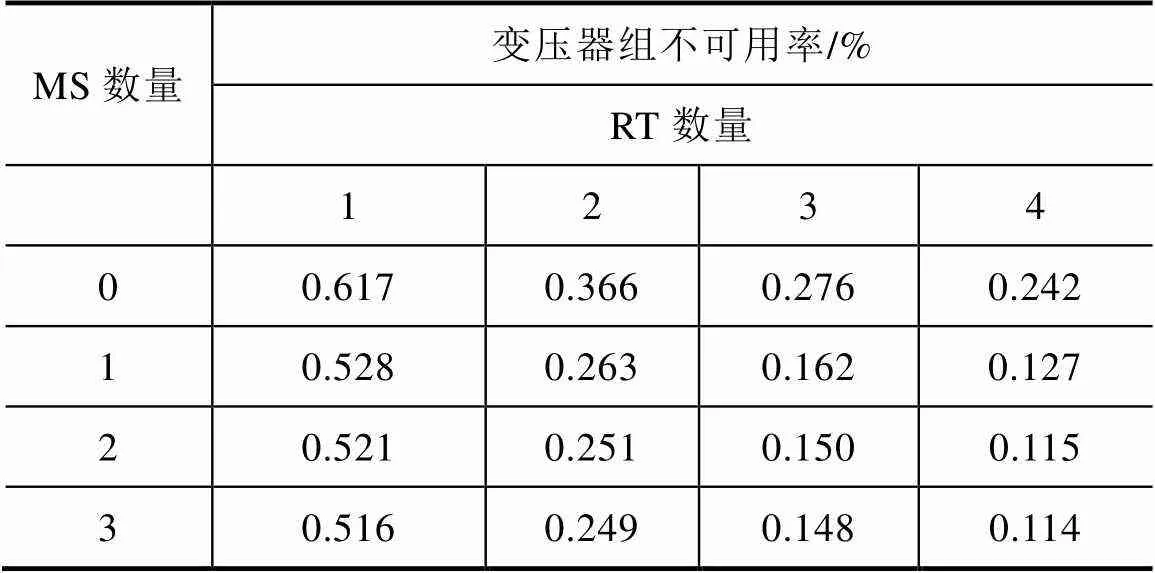
表4 强迫停运造成的变压器组可靠性指标-B区域

2）计划检修造成的系统缺供电量期望

由表5可见，若没有MS，则两地区都会因计划检修出现缺供电，但是B区域计划检修造成的缺供电量期望要远大于A区域，这是因为对采用单主变配置的变电站计划检修时，需要对供电负荷停电，而B区域中配置单台变压器的变电站比例比较高。当配有1台MS时，两区域不再发生计划检修造成的失负荷。

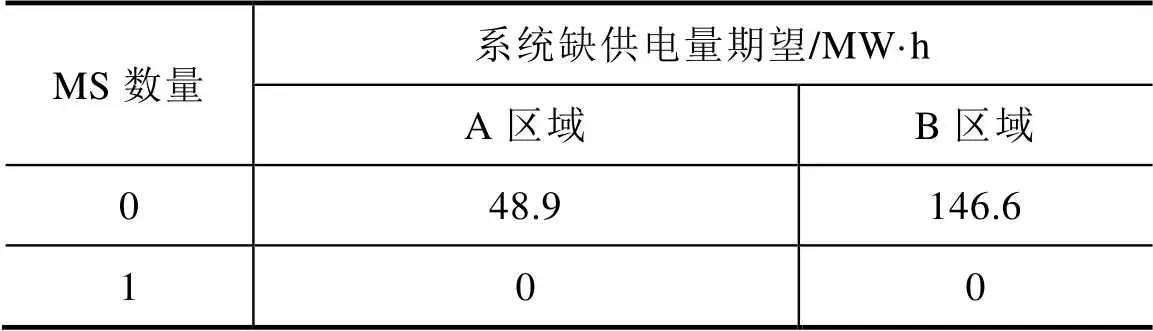
表5 计划检修造成的系统缺供电量期望

4.2 备用规划结果及分析

本文对两个不同区域进行规划分析，对比其不同备用类型以及数量对系统总费用的影响。RT的最大数量为4台，MS的最大数量为3台。含2台RT的费用计算结果见表6。

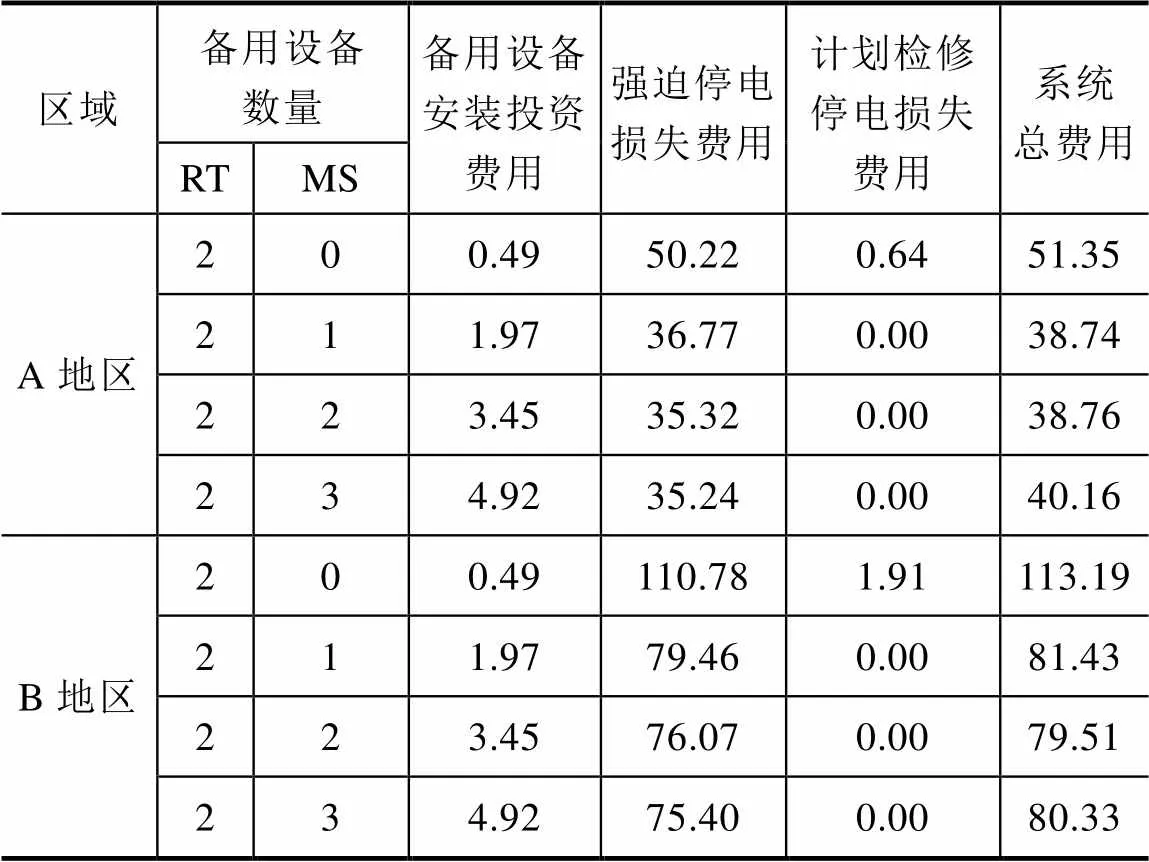
表6 MS配置数量对系统总费用的影响-2台RT（单位：106元/年）

由表6可见，A地区的计划检修带来的停电损失很少，这是因为A地区大部分变电站配置2台变压器，在计划检修时另外一台变压器会承担全部的负荷，因此不会失负荷；就B地区而言，MS数量从0增加到1时，增加的MS投资成本小于减少的计划检修停电损失。因此，仅从减小计划检修停电损失的角度，A地区无需配置MS，而B地区需要。

关于系统的总费用，系统的总费用随着MS的数量的增加呈现先降低后升高的趋势。这是因为，在变压器发生故障时，投入备用设备MS，会缩短故障停运时间，提高可靠性，因此降低了停电损失费用。在可靠性评估的蒙特卡洛算法中，投运MS缩短停运时间的这一影响，体现在变压器的时序状态模拟中。然而，另一方面，MS的配置却提高了MS的投资和运维费用。因此，系统的经济性是各部分费用综合作用的结果。对于区域A，RT为2台的情况下，MS数量从0增加到1时，系统总费用在降低，但是当MS数量增加到2台时，系统总费用在增加。由此可以看出：综合考虑计划检修和强迫停运下，区域A安装1台MS时，系统的经济性最优。对于B地区而言，在RT为2台的情况下，MS增加到2台时，系统的经济性最优。

5 结论

本文综合考虑计划检修和强迫停运的变压器组备用规划问题。以备用设备的种类和数量为决策变量，系统总费用最小为目标函数，建立计及可靠性的备用规划模型得到可靠性和经济性最优的规划方案。该模型使用序贯蒙特卡洛方法计算变压器组可靠性指标，并将可靠性指标转化为停电损失计入到规划方案的总费用。以区域所有变压器构成的变压器组为对象，分别对不同的两个区域进行规划。算例结果表明：

1）仅针对计划检修导致的停电损失时，是否需要配置MS的决策受区域变电站的构成类型影响。在以双主变的变电站为主的A区域，安排计划检修时不需要配置MS，但是在单主变的变电站较多的B区域需要配置MS，以弥补计划检修停电损失。

2）综合考虑计划检修和强迫停运下，在RT为2台的情况下，区域A安装1台MS时，系统的经济性最优。对于B地区，MS配置2台达到最优经济性。

[1] 丁明, 毕锐, 李小燕, 等. 基于FD法和模型组合的柔性直流输电可靠性评估[C]//中国高等学校电力系统及其自动化专业第二十三届学术年会论文汇编, 合肥, 2007.

[2] 陈炜骏, 周家启, 刘洋, 等. 特高压双12脉波直流换流站系统可靠性评估[J]. 电气应用, 2007, 26(12): 36-41.

[3] 李生虎, 马燕如, 陈鹏, 等. UHVDC系统可靠性分层等值与灵敏度分解[J]. 电力系统保护与控制, 2014(22): 9-17.

[4] 王遂, 任震, 蒋金良. 混合法在高压直流输电系统可靠性评估中的应用[J]. 电网技术, 2007, 31(12): 42-46.

[5] Xie Kaigui, Hu Bo, Singh C. Reliability evaluation of double 12-Pulse ultra HVDC transmission systems[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 210-218.

[6] 吴治均, 李明昆. 基于馈线路径集合法的并网型微电网可靠性评估[J]. 电气技术, 2016, 17(10): 17-22.

[7] 杨子成. 考虑地形影响及尾流效应的风电场可靠性分析[J]. 电气技术, 2017, 18(1): 71-76.

[8] 王杨, 谢开贵, 胡博, 等. 基于时序模拟的离网型微网可靠性分析[J]. 电工技术学报, 2016, 31(6): 206- 211.

[9] 别朝红, 李更丰, 谢海鹏. 计及负荷与储能装置协调优化的微网可靠性评估[J]. 电工技术学报, 2014, 29(2): 64-73.

[10] 中国南方电网有限责任公司. Q/CSG电力设备检修规程[S]. 北京: 中国电力出版社, 2014.

[11] 杜林, 袁蕾, 熊浩, 等. 电力变压器运行状态可拓层次评估[J]. 高电压技术, 2011, 37(4): 897-903.

[12] 彭鹄. 含风力发电的发输配电系统可靠性综合评估[D]. 重庆: 重庆大学, 2007.

[13] 郭永基. 可靠性工程[M]. 北京: 清华大学出版社, 2002.

[14] 何敏. 计及可靠性的配电变压器组检修及备用策略研究[D]. 重庆: 重庆大学, 2016.

[15] Hamoud G A. Use of markov models in assessing spare transformer requirements for distribution stations[J]. IEEE Transactions on Power Systems, 2012, 27(2): 1098-1105.

[16] 周莉梅, 范明天. 城市电网用户停电损失估算及评价方法研究[J]. 中国电力, 2006, 39(7): 70-73.

[17] 曾庆禹. 特高压交直流输电系统技术经济分析[J]. 电网技术, 2015, 39(2): 341-348.

[18] 洪思远. 计及经济性和可靠性的配电设备检修计划优化研究[D]. 广州: 华南理工大学, 2013.

[19] Billinton R, Yang H. Incorporating maintenance outage effects in substation and switching station reliability studies[C]//Electrical and Computer Engineering, 2005. Canadian Conference on, 2005.

[20] Hamoud G A. Assessment of spare transformer requi- rements for distribution stations[J]. IEEE Transactions on Power Systems, 2011, 26(1): 174-180.

Transformer reserve planning with the consideration of planned maintenance and forced outage of transformers

Wang Man Wang Yonghua

(China State Grid Chongqing Company, Jiangbei Branch, Chongqing 400044)

Planned maintenance for equipment can improve the health state of equipment and enhance the reliability of equipment and systems. However, the maintenance of transformer may cause the outage losses. The Monte Carlo simulation technique is used to calculate the reliability indices, and the planned maintenance and forced outage of transformers are considered into the reliability. In this paper, the spare transformer planning model is established based on the type and quantity of the spare transformer as decision variables and the minimum cost of transformers as an objective function. The enumeration method of optimal configuration of spare transformers is given. Spare transformers configuration in two different systems are researched in case study. The results show that MS configuration can increase system reliability. Under the given parameter of reliability and economy, decision of MS configuration is related to proportion of different types of substations in the system studied if interruption cost of planned maintenance is considered only. Considering interruption cost of planned maintenance and forced outage, optimal configuration number of spare transformers is related to proportion of different types of substations in the system studied.

transformer reserve; reliability evaluation; planned maintenance; forced outage; Monte Carlo Simulation

2017-09-30

王 曼（1992-），女，宁夏银川市人，硕士研究生，主要从事变电运检工作。