基于改进神经网络的电梯故障诊断

，

(1. 湖南电气职业技术学院，湖南 湘潭 411000；2. 湖南德力通电梯有限公司，湖南 株洲 412000)

1 引 言

受制于安装工艺、维保质量等影响，电梯在运行过程中产生非周期性的故障，干扰到人们的出行，影响人们的生活质量，甚至会造成严重的安全事故，危害到乘客的生命安全[1]。因此通过分析电梯各项运行数据，结合专家知识库，量化专家经验，在电梯出现故障时，准确、快速定位故障区域，查明故障产生原因，能够减小因电梯故障带来的经济损失，对于提高电梯安全和可靠运行具有重要意义[2,3]。本文研究一种优化的BF神经网络的电梯故障诊断模型。

2 神经网络算法分析

2.1 神经网络结构

人脑神经网络系统具有超强的自我学习能力，在外界持续刺激影响下，通过不断地学习，能根据不同的环境来处理问题[4]。上世纪40年代末，心理学家和数学家进行合作，提出了形式神经元的数学模型，为神经网络学习算法奠定了理论基础。经过相关学者和研究人员不断的完善，衍生出RBF等神经网络算法，广泛应用于信号处理、图像识别等领域[5]。神经网络算法有一个输入和输出两层，它们之间存在多层次的神经元链路，上世纪60年代末， M. Minsky将中间的多层链接简化为隐含层，降低问题处理过程的复杂度，Minsky神经网络算法结构如图1所示。

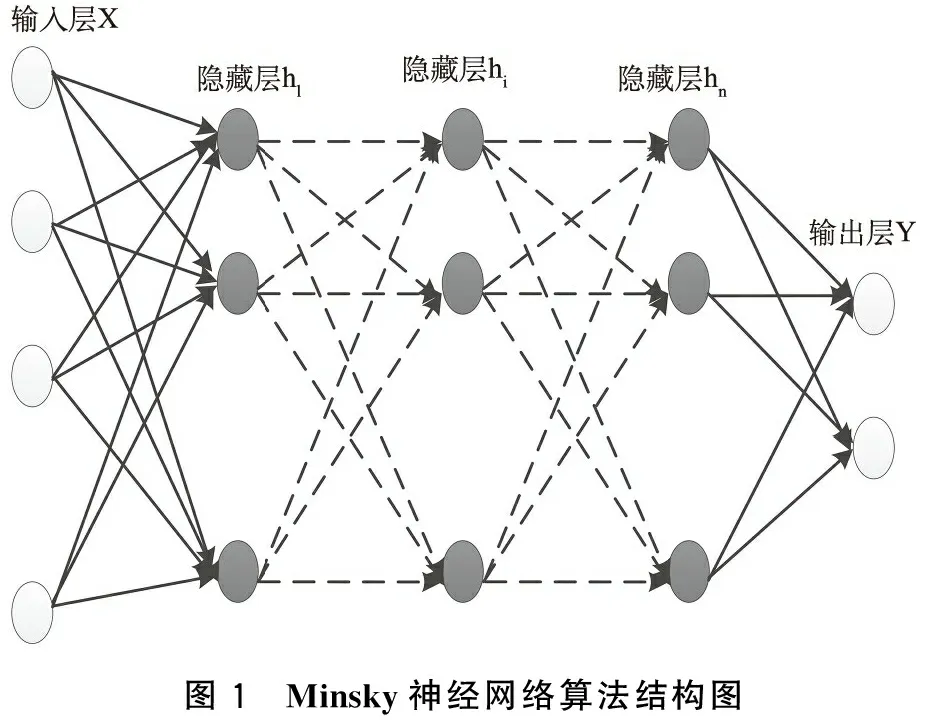
图1 Minsky神经网络算法结构图

图1中，外界输入信息数据，经过中间隐含层非线性函数的转换和处理，输出一组或多组结果。在神经网络算法中，隐含层是输入层和输出层的衔接层，类似于软件工程测试过程中的黑盒，具有非线性基函数特性。隐含层在训练集数据不断的刺激下，模仿人脑神经思维模式进行自我学习和成长，动态调整和优化隐含层的链路权重值，以适应各种比较复杂环境，对外界信息作出合理的判断。在隐含层，连续层中的神经元互相连接，每个神经元计算其输入的权重之和，而输出需要计算该值经过激活函数调整过的值。比如，该激活函数可为S形函数：

(1)

BP神经网络在训练过程中，需要引入目标误差函数，来判定网络模型的神经链路权值合理性，决定继续调整和优化网络权值的必要性。误差目标函数是用网络的期望输出与实际输出的误差平方和，即

(2)

其中，E(p)为样本个体均方误差，P为样本训练集。

2.2 优化的神经网络算法

神经网络算法在在计算期望值与实际值之间的距离时候，采用欧几里得公式，目标函数容易产生局部极值而无法得到最优值，因此，该算法存在一定的局限性。通过相关资料的查询，神经网络算法还存在收敛速度慢等缺陷。

针对神经网络算法存在的不足，可以从两个方面来处理，一是在误差目标函数中，用马氏距离公式来替代欧几里德距离公式，二是在神经网络算法中引入粒子群算法来达到提高收敛速度的目的。

(1)马氏距离来计算误差目标函数的距离

(3)

(2)基于粒子群的神经网络的优化算法

Kennedy博士等在研究鸟类觅食的过程中，将鸟群整体视为一个多维空间，食物在多维空间的某一个坐标点，每一只鸟看作为多维搜索空间的一个粒子，那么可以转化为多维空间的最优求解问题。该算法在收敛性方面具有先天性优势[1]。假定在D维空间，粒子群中任意一个粒子都可以看作为多维空间的一个向量位置点，在任意时刻t，粒子在此位置点具有飞行速度，分别用Xi=(xi1，xi2，…，xiD)和Vi=(vi1，vi2，…，viD)来表示。小鸟(粒子)在觅食的运动过程中，其所在的位置就是空间的一组解，且存在一个最优的位置矢量点Pi，Pi=(pi1，pi2，…，piD)。对于整个粒子群体来说，在D维空间也存在一个全局最优的位置Pg，是所有Pi(i=1，2，…，n)中的最优。粒子在运动过程中，粒子的速度和位置是动态改变的，其计算公式为：

(4)

基于粒子群优化的神经网络算法步骤[6]：

①初始化粒子位置和速度，并分别计算出每个粒子的适应度；

②计算每个粒子最优值和群体最优值；

③通过公式(4)更新粒子位置和运行速度；

④采用马氏距离公式计算，判断是否得到最优的目标函数值，如果目标函数值小于无穷小的正数，那么终止循环并输出最优解；反之执行第二步，对粒子适应度重新计算并赋值。

⑤将上步输出的最优解，赋值给BP网络的最优权值和阈值。

3 实例分析

3.1 建立模型

在电梯运行过程中主要是收集电梯关门、蹲底、冲顶、停电、运行过程中开门、超速、非平层区域开门、非平层区域停车等九类故障信息。也就是说9个电梯故障特征参数，根据神经网络结构，设置本文的输入神经元节点为9，神经网络的输出神经元节点为1，即电梯运行故障特征代码。以9组故障数据的样本中35组数据作为神经网络的训练数据，部分测试数据结果如表1。基于粒子群的BF神经网络模型的主要参数设置为：迭代次数为1 000，粒子群规模为20，粒子加速度为C1=C2 =1.51。

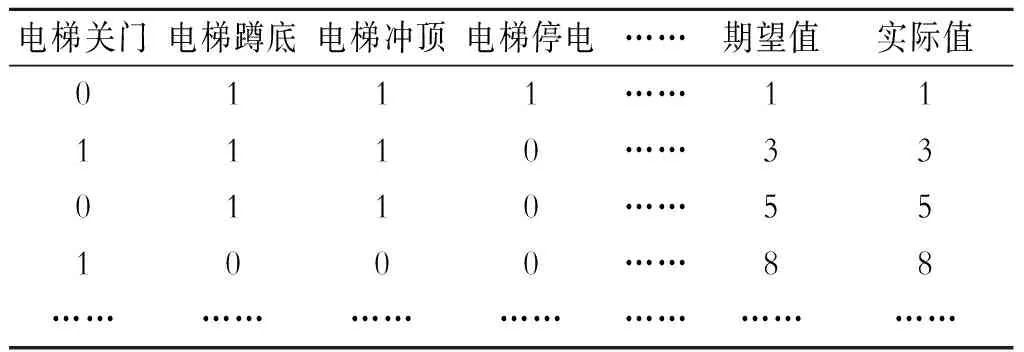
表1 部分测试数据结果表

注：1表示为正常，0为存在故障。输出的数据表示电梯诊断故障代码。

通过使用训练样本对本文研究的改进BF神经网络电梯故障模型及常规BF神经网络建立的电梯故障诊断模型进行训练，得到两种模型的误差收敛曲线如图2和图3所示。可以看出，使用本文的改进BF神经网络模型后，收敛精度和收敛效率均有大幅度提升。

3.2 电梯故障诊断测试结果分析

以35组故障数据的样本中的4组数据作为神经网络的测试数据。使用上述建立的神经网络配电梯故障诊断模型对测试数据进行测试，即将测试数据的故障特征输入建立的神经网络电梯故障诊断模型中，将诊断模型输出的故障征兆区域与实际样本中的故障征兆区域进行对比，由于篇幅原因，只列出了5个故障区域的数据。神经网络故障诊断模型输出数据见表2所示。

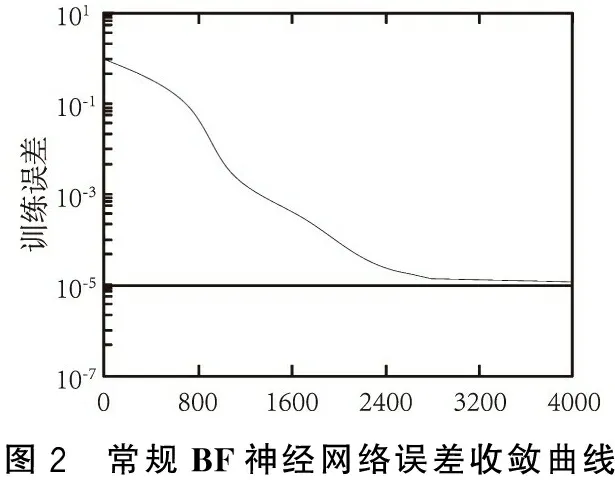
图2 常规BF神经网络误差收敛曲线

图3 改进BF神经网络误差收敛曲线

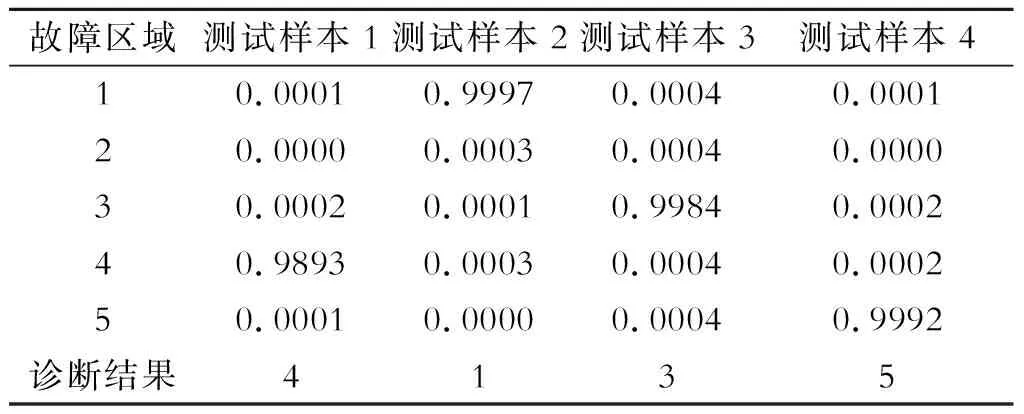
表2 神经网络故障诊断模型输出结果

数据分析：表2的第1列表示故障征兆区代码，第2列到第4列是测试样本对应的故障数据输出预测值。测试样本1在故障区域4的输出值为0.9893，其他故障区域输出数值非常小，说明故障区域4出现了电梯运行故障，其他测试样本数据的分析类似此方法。通过表2的数据分析，说明了本文的故障诊断模型达到了预期目标。

4 结束语

电梯运行过程中的故障诊断方法的研究，有利于电梯故障的快速定位，变电梯故障事后诊断为事前预警，提高电梯的安全性和可靠性，能够减小因电梯故障带来的经济损失，对于提高电梯的安全运行具有重要意义。

通过实例分析可知，基于神经网络的电梯故障诊断方法具有较高的准确率。相比常规的神经网络建立的电梯故障诊断模型，基于神经网络的电梯故障诊断方法精度更高，故障诊断模型的输出值更加接近实际值。

参考文献：

[1] 冯 雪. 电梯运行监控预警系统研究与实现[D].中国科学技术大学,2017.

[2] 张 阔,李国勇,韩方阵.故障树法和改进PSO-PNN网络的电梯故障诊断模型[J].中国安全生产科学技术,2017,13(09):175-179.

[3] 王志平. 基于高速电梯运行特征大数据分析的急停故障诊断技术及应用[D].浙江大学,2016.

[4] 梁峻平.电梯故障诊断中神经网络技术的应用[J].科技与企业,2014,(23):65.

[5] 张广明,邱春玲,钱夏夷,等.模糊层次分析法和人工神经网络模型在电梯风险评估中的应用[J].控制理论与应用,2009,26(08):931-933.

[6] 熊瑞庭. 基于模糊神经网络的电梯故障诊断系统的研究[D].武汉理工大学,2009.