湍流模型对离心风机数值模拟的影响分析及试验验证

于胜剑，王志强，罗玉娟，赵修宇，赵哲斌

（1. 大连船舶重工集团设计研究院有限公司，辽宁大连 116000；2. 大连船舶重工集团有限公司，辽宁大连116000；3. 上海船舶设备研究所，上海 200031）

0 引言

离心通风机是一种广泛应用于工业、农业等领域的设备[1]。在过去，离心风机新产品设计研发或对原有设备进行改进的主要流程是结构设计、样机试制、试验、结构调整，而离心风机设计效果的验证必须通过样机制造和试验来实现[2]。随着计算机硬件的发展和计算流体动力学（Computational Fluid Dynamics，CFD）技术在叶轮机械领域的成熟应用，数值模拟在离心风机的流动分析、性能预测以及优化设计中起到了越来越重要的作用，通过计算进行优化调整后，再进行样机的制造和试验，使离心风机的整个设计流程周期缩短、成本降低[3-6]。

数值模拟又叫数值试验，数值模拟的主要流程包括针对研究对象建立反映问题（工程问题、物理问题等）本质的数学模型、进行模型处理、划分网格、选用合适的湍流模型、设置边界条件以及计算分析等。其中，选择的湍流模型是否合适，对数值模拟计算所需的时间、计算结果的准确性等都会产生较大的影响。工程湍流理论中，多种模型各有其优缺点和适用条件。在叶轮机械流场计算中，常用的湍流模型有BL模型、SA模型和k-ε模型等。虽然这些湍流模型已经广泛应用于叶轮机械数值模拟领域，但至今还没有得到一个有效的通用湍流模型。因此，在离心风机数值模拟研究中，根据实际需求，对比分析出一种更合适、更准确的湍流模型是十分必要的。

本文对特定的某型离心风机进行了数值模拟计算，分别采用了BL、SA和k-ε三种湍流模型进行计算，分析了湍流模型的选取对数值结果的影响，并将其与样机试验数据进行对比。

1 计算模型建立及网格设置

本文研究的离心风机设计流量为11000 m3/h，全压3200 Pa，转速2920 r/min。风机主要由进口集流器、叶轮和蜗壳组成，其中，叶轮为后弯型式。图1为离心风机三维图，图2为主要部件关系的透视图。该离心风机的主要尺寸参数为：叶轮叶片进口直径D1为328 mm，叶轮叶片出口直径D2为520 mm，叶轮进口宽度b1为138 mm，叶轮出口宽度b2为102 mm，叶片数Zn为 12，叶片进口安装角β1A为 28°，蜗壳宽度B为298 mm。

在构建计算模型的过程中，本文对风机结构进行了简化。风机主要被分成进口集流器、叶轮和蜗壳 3个流动区域模型，其中进口集流器在来流方向加了一定的延伸，如图3所示。

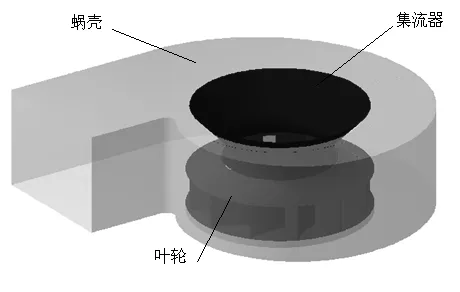
图1 离心风机三维图

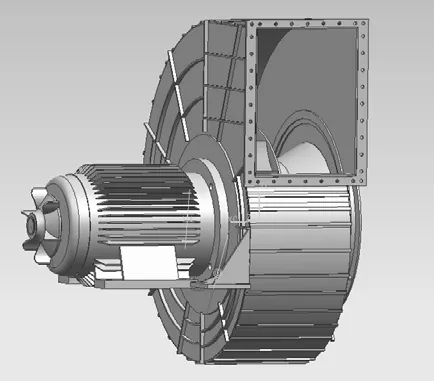
图2 离心风机透视图

图3 离心风机流动区域模型

离心风机同时包含转动部件和静止部件，为了减小网格对计算结果的影响，需要使用合理的网格生成方法。网格划分时，首先对进口集流器、叶轮和蜗壳3个区域分别划分网格，然后将 3个部分单独生成的网格组装起来，如图5所示。网格处理时，为了在几何上尽可能地与离心风机真实结构相似，考虑了叶轮前盘和后盘的厚度、进口集流器的厚度及轮毂结构。同时，在蜗壳、叶轮等近固体壁面处对网格进行加密，以确保能较为准确地反应风机内部流动情况。整机网格数约为 210万，网格无关性验证结果表明，本文计算网格数满足无关要求。

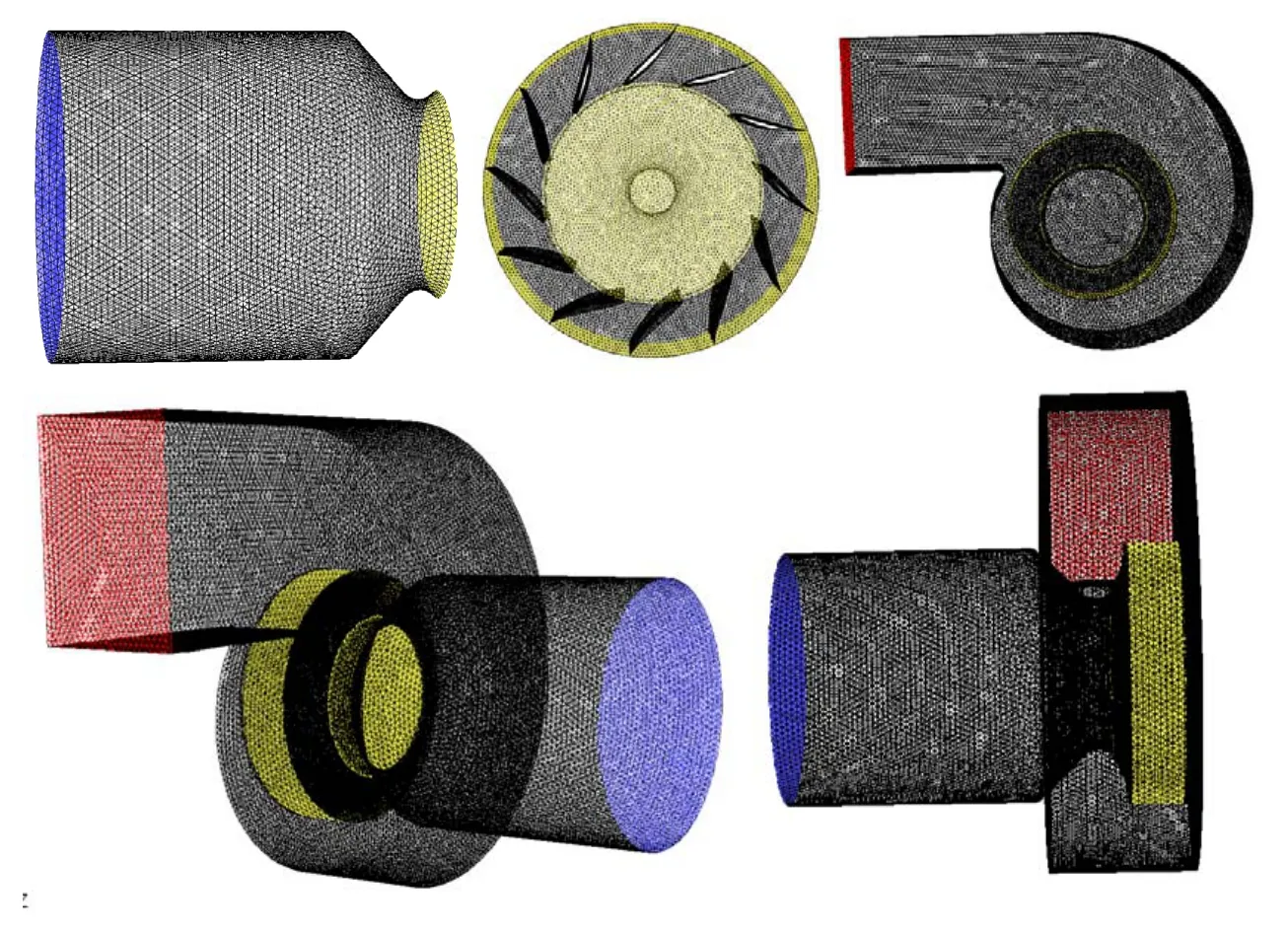
图4 离心风机网格划分

2 数值计算设置简介

本文分别采用了BL、SA和k-ε三种湍流模型对离心风机进行计算。由于存在旋转区域，本文采用MRF方法处理动静结合部分。考虑到计算介质为空气，其流速低且压比小，因此可视为不可压缩流体。空气在风机中流动时，传热过程基本可以忽略，因此不涉及能量方程的求解。在计算中，轮毂、叶片表面以及蜗壳壁面采用无滑移、绝热边界条件，叶轮转速为2920 r/min。假设上游均匀来流，流动方向与界面垂直，因此入口选用流量进口边界条件；假设稳定出流，因此出口选用自由出流边界条件。

3 计算结果分析

本文主要分析不同湍流模型对数值计算的影响，工作中采用同种几何结构、网格数目的数值模型进行计算分析。

3.1 总性能分析

图5、图6给出了3种湍流模型下计算获得的离心风机特性图。在图5中可看到：3种湍流模型计算得到的流量-全压曲线整体变化趋势相同，全压都随着风量的减少而增加。但 3种模型得到的具体数值有明显差异，在相同流量的情况下，使用BL湍流模型计算获得的全压值都低于使用 SA模型和k-ε模型计算获得的值；而SA模型和k-ε模型对应的流量全压曲线吻合度较高。流量-效率曲线图如图6所示。从图6可以看到：不同湍流模型对应曲线的整体变化趋势相同，但相比其余2个湍流模型，BL湍流模型计算获得的效率在计算流量范围内较低，这一点在额定流量附近区域内尤其明显，而其余 2个湍流模型对应的流量效率曲线基本相同。通过对比分析使用不同湍流模型计算得到的总性能，可以看出：使用SA模型和k-ε模型计算获得的性能曲线比较一致，而使用BL模型计算获得的性能值则普遍较低。

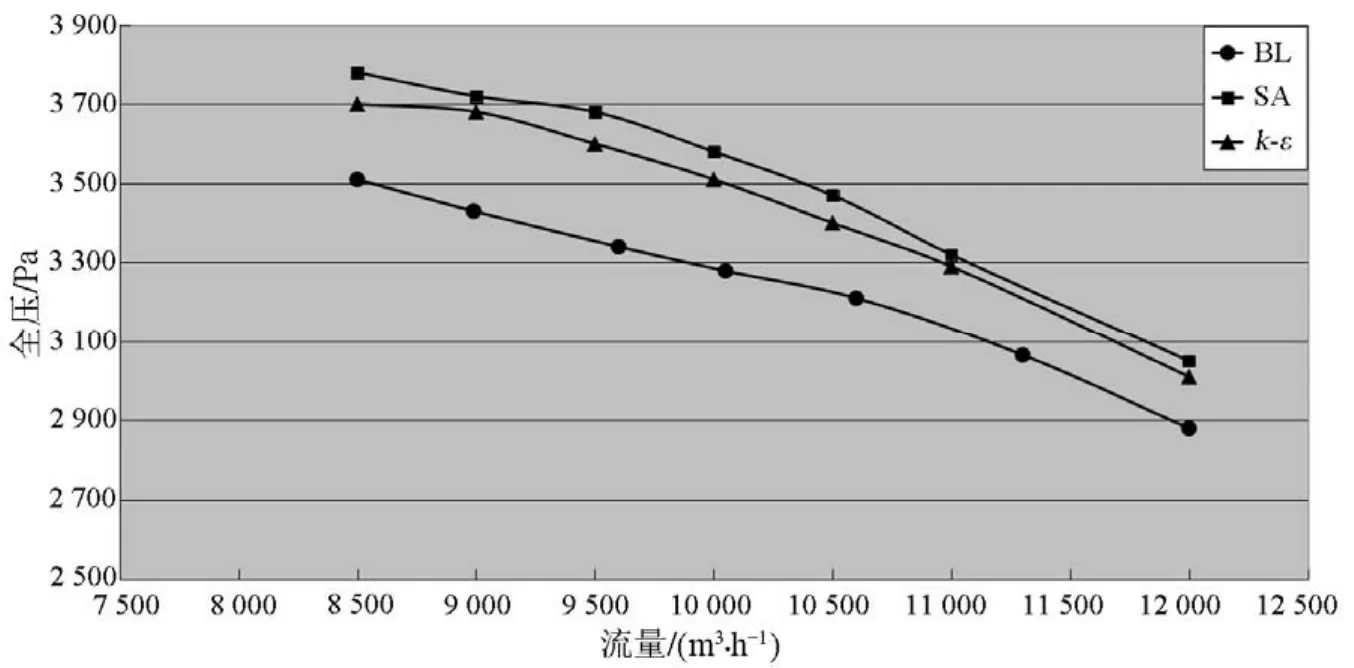
图5 离心风机流量全压曲线

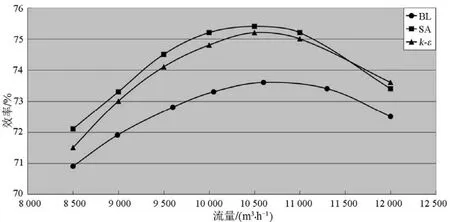
图6 离心风机流量效率曲线

3.2 内部流场对比分析

前文分析了使用不同湍流模型进行数值模拟对离心风机总性能计算结果的影响。本节通过对比分析额定工况下不同湍流模型计算得到的叶片通道内速度矢量分布及风机内部剖面的流场，探索了湍流模型对于风机内部流场的影响。

图7、图8及图9分别给出了额定工况下，3种叶高处（约10%、50%及90%）的静压分布图。从图7中可以观察到：BL模型在12点、3点及4点方向的通道内存在高压区，SA模型和k-ε模型都是在3点方向的通道内存在高压区。从图8和图9中可以发现：SA模型和k-ε模型得到的叶片通道静压分布形式类似，BL模型得到的静压分布形式则呈现出较大的不同；在50%、90%叶高处，多个叶片通道内BL模型的增压能力都弱于其它两种模型。

图10给出了额定工况下离心风机内部某剖面上气流速度矢量分布示意图，该剖面通过旋转轴且垂直于X坐标方向。从图中可以看到：3种湍流模型都能很好地捕获发生在集流器弯曲段附近的气流增速现象以及发生在后盖板轴套处的气流分离现象。BL模型获得的结果显示：左右叶片通道前盖板处存在气流分离区，右边通道内的低速区域范围比左边的大，在蜗壳内近集流器左侧出现了旋涡流动分布。SA模型计算结果显示：左右叶片通道前盖板处也存在气流分离区，左边通道内低速区往低叶高处发展的程度比右边的大，在蜗壳内近集流器左侧同样出现了旋涡流动分布。k-ε模型显示：左右通道内的低速区范围与SA模型所显示的差不多，在蜗壳内近集流器左侧也出现了旋涡流动分布。对比3种湍流模型计算得到的流场，可以发现：在近集流器右侧壁面处，BL模型得到的气流速度很大，而SA模型和k-ε模型得到的气流速度都很小。相较而言，SA模型和k-ε模型得到的结果更符合流动规律。

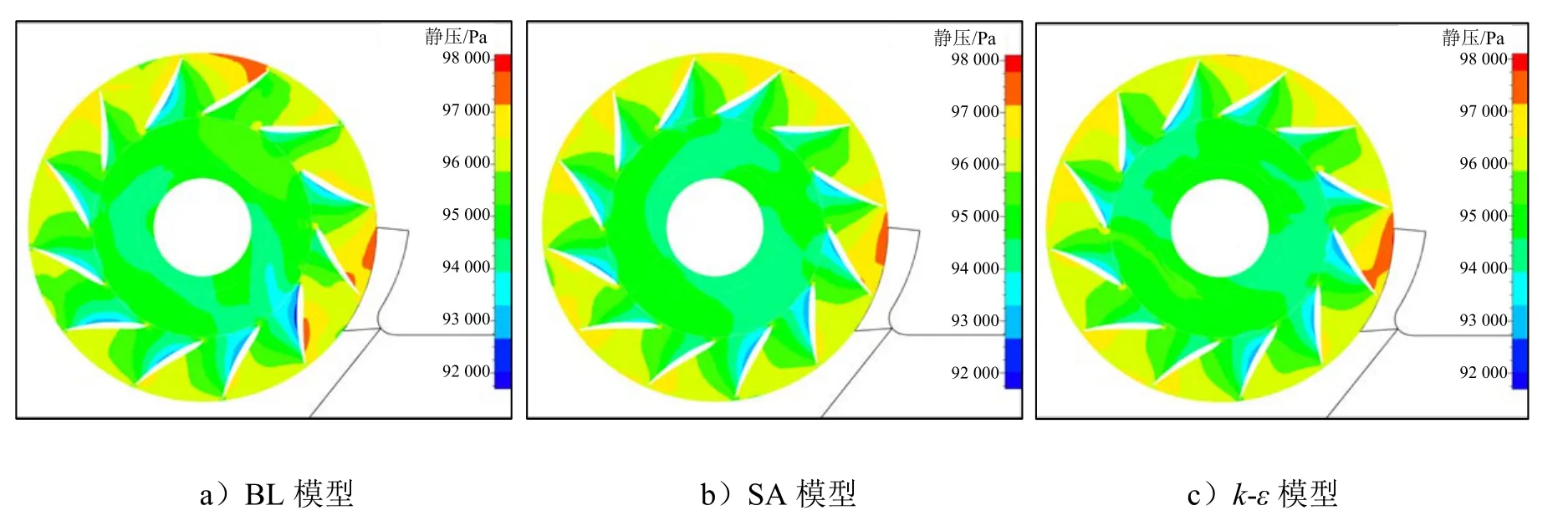
图7 额定工况下，约10%叶高处的静压分布图

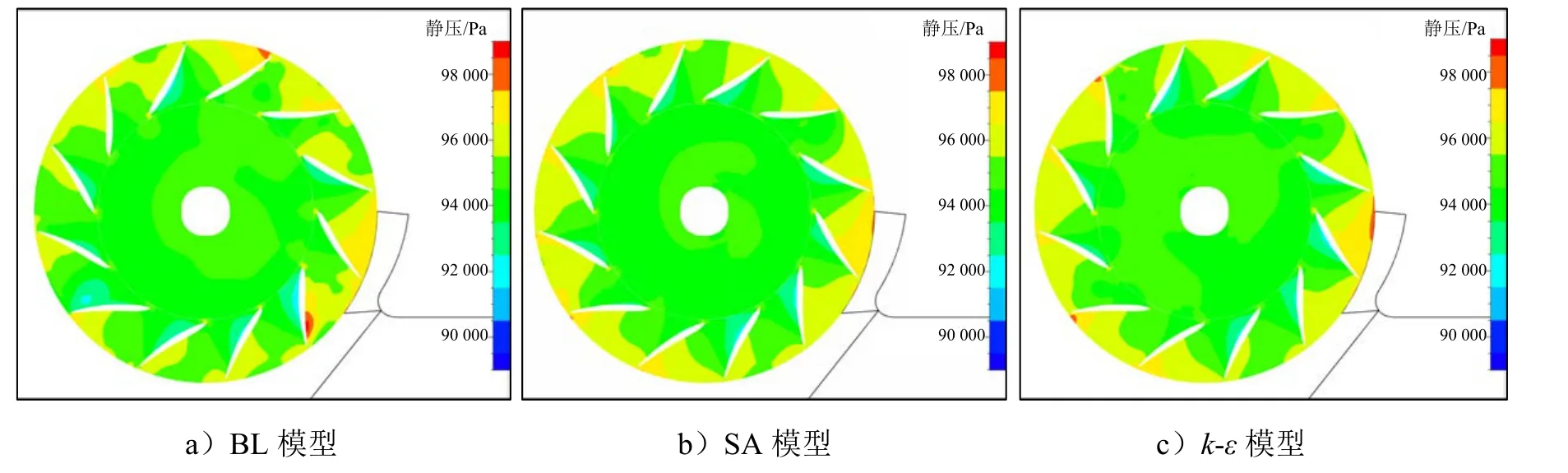
图8 额定工况下，约50%叶高处的静压分布图

图9 额定工况下，约90%叶高处的静压分布图

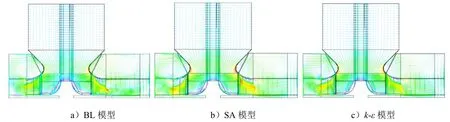
图10 额定工况下，风机内相对速度矢量分布剖面图

从以上分析可以看出：3种湍流模型计算获得的离心风机内部流场整体上相似，都能够反映风机内部流动特性。但分析静压分布和速度矢量分布细节可以发现：SA模型和k-ε模型获得的结果相对更合理。

3.3 试验结果对比分析

图11和图12为3种湍流模型计算获得的性能曲线与离心风机试验曲线的对比图。这 2幅图表明：不同湍流模型计算获得的性能曲线整体走势都与试验曲线相似，说明了数值模拟计算结果具有一定的可靠性；采用k-ε模型计算获得的性能曲线与试验获得的性能曲线吻合度更高，说明了采用k-ε模型能够获得更为可靠的结果。

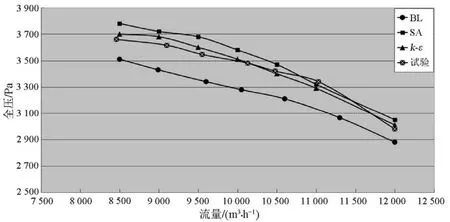
图11 离心风机流量全压曲线（模拟与实验对比图）

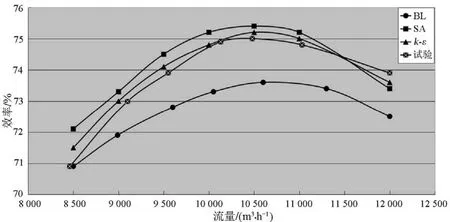
图12 离心风机流量效率曲线（模拟与实验对比图）

4 结论

使用 3种不同湍流模型对某型离心风机进行数值模拟，通过分析模拟得到的计算结果，并将结果与该型风机的试验数据进行对比，可以得到以下结论：1）采用这 3种常用的湍流模型获得的风机总性能变化趋势都与试验结果相吻合，3种模型计算得到的内部流场也大体相似，因此，数值模拟的结果是有参考意义的；2）从细节上看，k-ε模型的总性能计算值与试验值更为接近，相较于SA模型，其得到的流动细节也更符合流动规律，因此，在后续工作中将主要采用k-ε模型。

[1] 成心德. 离心风机[M]. 北京: 化学工业出版社,2007.

[2] 曹淑珍, 祁大同, 张义云, 等. 小流量工况下离心风机蜗壳内部的三维流动测量分析[J]. 西安交通大学学报, 2002, 36(7): 688-692.

[3] 丁可金, 孙玉祥, 顾军威, 等. 船用离心风机改进计算与试验研究[J]. 风机技术, 2009(3): 15-17, 20.

[4] 徐长值, 毛义军. 离心风机整机三维流场的数值模拟[J]. 风机技术, 2005(5): 1-4.

[5] 丁可金, 孙玉祥, 鞠毅, 等. 离心风机叶轮内部流场数值模拟[J]. 风机技术, 2010(6): 24-26.

[6] 陆蓓蕾, 陈瑞球, 石富金. 离心风机的三维数值计算[J]. 煤矿机械, 2005(4): 23-24.