由一道模考题展开的微专题探究

江苏省常州市第一中学

田秀权 丁春梅 (邮编：213003)

1 试题呈现

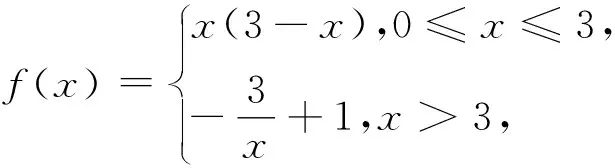
解法简析函数y=f(x)-m有四个不同的零点，等价于函数y=f(x)与y=m对应的图象有4个不同的交点.作出y=f(x)的图象，如图所示.

2 专题探究

教材不提函数渐近线概念毫不影响渐近线在函数中的地位，函数渐近线在各类模考、甚至高考题中频繁地展示着它的“妙曼身姿”；再者，教材中导数概念和双曲线渐近线的概念的学习已经为极限思想奠定了一定的基础.故笔者以函数渐近线为对象进行微专题训练和探究.

以下是专题探究过程简录.

2.1 初步探究 生成概念

问题1观察并说出下列曲线的渐近线.

(2)函数y=ax(a>0,a≠1)；

(3)函数y=logax(a>0,a≠1)；

(4)函数y=tanx.

问题2怎么理解函数渐近线的概念？

(通过学生的思考、交流，老师的点拨、引导……)归纳出概念：图象上的点M沿着曲线无限远离原点时，如果点M到一条直线的距离无限地趋近与零，那么这条直线称之为这个函数图象的渐近线.

设计意图利用最基本的初等函数模型引入课题，并由此生成函数渐近线的概念，情境上让学生感到亲切熟悉，水到渠成，知识上让学生由感性认知上升到理性判断，于无形中引导学生按照既定目标，追求新知识.

2.2 深入探究 突出“函数模型”

(1)“幂函数型”函数的渐近线探究

所谓“幂函数型”函数是指以幂函数为研究对象，对其实施一系列图象变换后得到的函数.

问题3在理解函数渐近线的基础上，重新思考上述题目.

问题4其他条件不变，把函数在x≥0时的解析式改成：

结果如何？

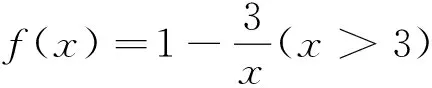
(2)“指数型”函数的渐近线探究

所谓“指数型”函数是指以指数函数为研究对象，对其实施一系列图象变换后得到的函数.

问题5其他条件不变，把函数在x≥0时的解析式改成：

(3)“对数型”函数的渐近线探究

所谓“对数型”函数是指以对数函数为研究对象，对其实施一系列图象变换后得到的函数.

问题6设函数

评注函数y=logax(a>0,a≠1)存在渐近线x=0,对其实施一系列图象变换后得到的“对数型”函数仍然存在渐近线；比如题中y=lg(x+1)存在渐近线x=-1.

(4)“混合型”函数的渐近线探究

所谓“混合型”函数是以两个或两个以上初等函数为研究对象，对其施加有限次的加、减、乘、除、乘方、开方运算得到的函数.

通过仔细研究发现，“活跃”在近几年模考、高考试题中的“混合型”函数主要有：y=xex,

,

,y=xlnx,

,

等.

图1

图2

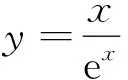
评注函数渐近线的求法：

(1)当自变量x→∞时，y→c(c是常数)，则y=c是函数的一条水平渐近线；

(2)当自变量x→x0(x0是常数，往往是函数的间断点)时，y→∞,则x=x0是函数的一条垂直渐近线；

(3)对于渐近线方程是y=ax+b(a≠0)的斜渐近线，这里不做探究.

设计意图在广义数学模型观下，数学是研究“模型”的科学.怀特海在《数学与善》一文中说：“数学的本质特征就是：在从模式化的个体做抽象的过程中对模式进行研究”“模型”建构是通向数学创造的阶梯，数学教学中帮学生建立、总结、提炼数学“模型”，一方面有助于学生对知识本身的理解和掌握，另一方面更为知识、方法的迁移提供了必须的“前验知识”.

3 经典探究 彰显能力

问题9(2017届湖南五市十校第四次模拟考试第12题)已知f(x)=xex,g(x)=f2(x)+tf(x)(t∈R),若满足g(x)=-1的x有四个值,则t的取值范围为______.

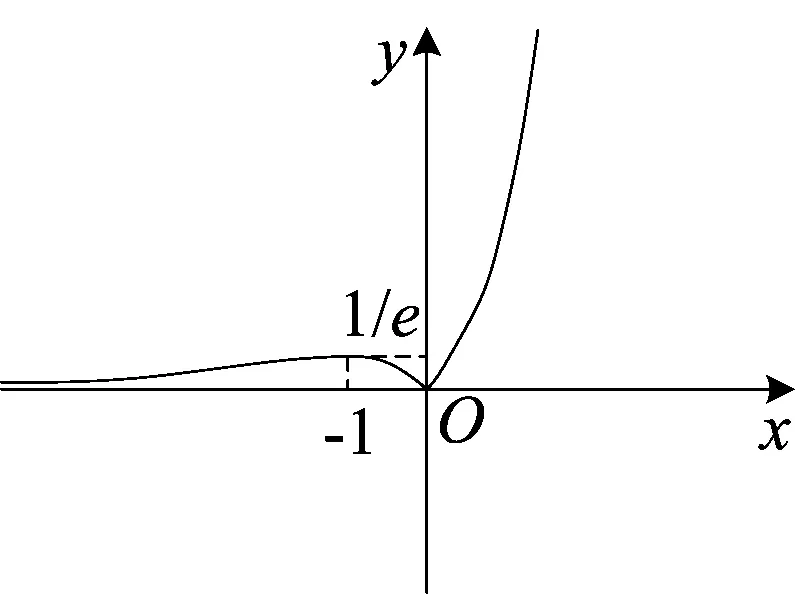
图3

解因为满足g(x)=-1的x有四个值，所以f2(x)+tf(x)+1=0有4个根.作出f(x)=xex的图象如图3(当x→-∞时，y→0,故函数f(x)=xex存在渐近线y=0)所示，令m=f(x),则

再往海边的话，就该到Cantolio了。这家酒庄成立于70年代，其中一片葡萄藤直接种在海滩上，海滩遍布钙质岩石裂缝。这片葡萄田需要人工种植和采摘，每年的数量非常有限。Cantolio凭借其高分酒质及高性价比，着实让人眼前一亮。实际上这个酒庄的实力早已彰显，从2013年起连续三年在“柏林葡萄酒大奖赛”、“亚洲葡萄酒大奖赛”和“布鲁塞尔世界葡萄酒大赛”中拿下金银奖，意大利最权威的葡萄酒指南“Luca Maroni”为其评出了90分的高分。如此喝了一圈，最后不如到亚得里亚海边去大快朵颐，这里的鱼虾非常鲜美！

问题10(2016年高考数学全国卷Ⅱ理科第21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(1)求a的取值范围；

(2)略.

这道题解法较多，零点存在定理的方法难度较大、对学生能力要求较高，这里不再赘述.笔者重点介绍函数渐近线在此题中的应用.解法如下：

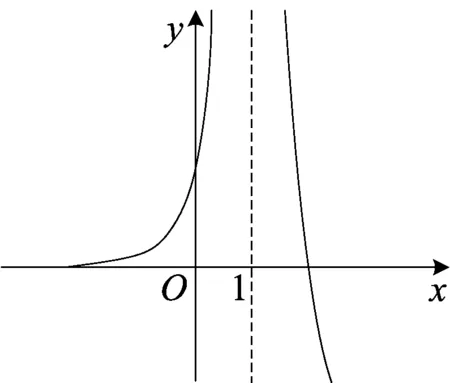
图4

图5

方法二令(x-2)ex+a(x-1)2=0,(x-2)ex=-a(x-1)2.令g(x)=(x-2)ex,g′(x)=(x-1)ex.

当x∈(1,+∞)时，g′(x)>0,函数单调递增；当x∈(-∞,1)时，g′(x)<0,函数单调递减；x→-∞,y→0,故函数存在渐近线y=0.

令h(x)=-a(x-1)2,h(1)=0,作出g(x)=(x-2)ex的图象如图5所示.所以a∈0,+∞.

设计意图经典的模考题、高考题对教学有一定的导向性和示范性作用，通过对经典题的研究让学生体会渐近线的“价值”，以提升学生学习的积极性、激发学生学习的热情.迁移是问题解决的核心，从学习迁移理论上看，教育的目的不仅在于使学生获得知识、技能和行为方式，更重要的是要促使学生能将已经掌握的知识、技能和行为方式应用到新问题解决过程中去，以提升学生的思维品质和综合能力.

3 几点感悟

3.1 微专题探究为什么“探”？

鉴于时间的限制和进度的要求，很多老师的讲评只是停留在就题讲题的层面，以讲清题目思路、方法的来龙去脉为目的，而不舍得把时间“浪费”在错因的分析以及针对错因展开的微专题探究上，这在一定程度上导致了学生“前讲后忘”、“错了还错”的现象.在高三数学复习过程中，结合考试的重点、热点内容，在学生的易错点处不失时机的展开微专题探究，可以使错因明朗化、知识系统化、方法清晰化、思维深刻化.

3.2 微专题探究“探”什么？

引导学生进行微专题探究的基点是准确把握学情和深刻理解教学内容的本质，课堂教学设计应牢牢拴住这两个基点.认识函数渐近线的本质必须研究清楚两个问题：一是什么是渐近线；二是研究渐近线的方向和方法是什么.这两个问题一个是知识，一个是方法，在研究、弄清这两个问题的基础上探究、归纳函数渐近线的常见“函数模型”，课堂自然朝着系统、深度的方向发展.教学中教师只有深刻理解教学内容的本质，才能抓住这个本质明确探究的内容和方向.

3.3 微专题探究如何“探”？

“微专题”的设计要条理清楚不零散，结构简洁有深度.如何“探”？ 才能达到知识系统化更是思维深刻化目的，这取决于对问题的设计.一方面要重视对“问题串”的设计，设计一系列相互“关联”的、有“层次性”的“问题串”可以引导学生进行系统的、连续的思维的活动；另一方面要重视对问题的变式探究，在比较、变化中体会问题的“形变而质不变”，进而引导学生深刻理解知识的本质.

1 张乃达.抽象与模式[M].郑州:大象出版社,2004

2 殷孝锋.见“微”知著─微专题在数学思维训练中的应用[J].中学数学月刊,2016(3)