上教版高三数学教材中样本标准差公式合理性初探

华东师范大学附属周浦中学

凌燕萍 (邮编：201318)

上教版高三数学(试用本)中给出的样本方差、样本标准差的计算公式不同于其他版本的教材，教材中也没有给出说明，给广大老师的教学和学生的学习带来不少困扰.

方差和标准差给出的是一组数据偏离平均数程度的大小，数值越小，说明这组数据越向平均数集中，数据越大，说明这组数据偏离平均数的程度越大.在某些统计问题中，做不到也没必要对总体中的每一个个体进行研究，就需要从总体中抽样研究.那么怎么用样本的标准差来估计总体的标准差呢？不同的版本有不同的说明：

1 对方差和标准差的定义

1.1 上教版

1.2 人教版

1.3 苏教版

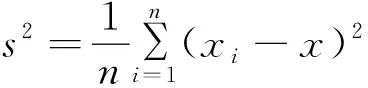
1.4 《教育统计与测评导论》

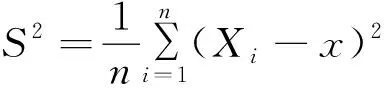
2 典型例题

2.1 上教版高三数学(试用本)第108页例1：

某赛季甲乙两名篮球运动员在若干场比赛中的得分情况如下：甲：18、20、21、22、23、25、28、29、30、30、32、34.乙：8、13、14、16、23、26、28、33、38、39、48.问谁的比赛成绩比较稳定.(结果精确到0.01)

解析易得甲乙两名运动员每场得分的平均值均为26分.

设甲得分的标准差为s1,记甲的每场得分与其得分平均值的差的平方和为∑1,则∑1=(18-26)2+(20-26)2+(21-26)2+…+(32-26)2+(34-26)2=296,

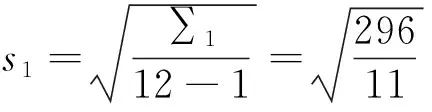
设乙得分的标准差为s2,同理得

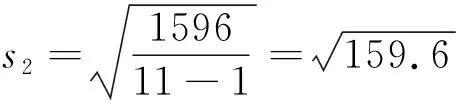
因为s2>s1,所以甲运动员的比赛成绩比较稳定.

2.2 上教版高三数学(试用本)第106页例3:

为了解某体校学生长跑的情况，观察随机抽取的20名学生一周内跑步的累积千米数，在各个区间内频数记录如下表所示：

表1

求一周内学生平均累积跑步的千米数及其标准差.

解析先求出各个区间的中点值：8、13、18、23、28、33、38.

s=

本题中，n=20,m=7.经计算得：x=24.5,s=8.29.

因此可知：学生平均每周累计跑24.5千米，标准差为8.29千米.

2.3 2009年重庆高考卷(文科)

从一堆苹果中任取5只，称得它们的质量如下(单位：克)125 124 121 123 127则该样本标准差s=______(克)(用数字作答)．

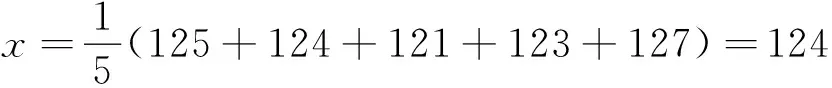
以上三个例题都用到了样本标准差，由于教材不同，选用了不同的公式，那么，上教版中的样表标准差为什么要除以n-1？这么做能消除系统偏差的依据是什么呢？对应地，样本均值为什么没有除以n-1呢？

3 基本原理

根据样本统计量对相应总体参数所作的估计叫做总体参数估计，总体参数估计分为点估计和区间估计.点估计是指用某一样本统计量的值来估计相应的总体参数的值.比如，用样本均值和样本标准差来估计总体平均数和总体标准差就是点估计.

点估计的评价标准是：无偏性、有效性、一致性.

3.1 无偏性

当用某一个样本统计量的值估计总体参数值时，总会有所偏差，有的大于总体参数，有的小于总体参数，如果一切可能个样本统计量的值与总体参数值偏差的平均值为0，这种统计量就是总体参数的无偏估计量.

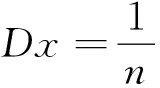
两个定义：

μ=E(X)；

σ2=D(X)=E(X-EX)2.

数学期望有以下性质：

(1)常数性E(C)=C,其中C为常数；

(2)齐次性E(CX)=CE(X)；

(3)可加性E(X+Y)=E(X)+E(Y)；

(4)独立性E(X·Y)=E(X)·E(Y)，其中X,Y相互独立.

方差具有下列性质：

(1)常数性D(C)=0，其中C为常数；

(2)二次性D(CX)=C2D(X)；

(3)可加性D(X+Y)=D(X)+D(Y)，其中X,Y相互独立.

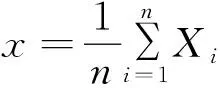
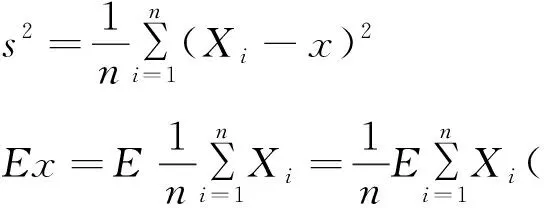
可见：样本均值x是总体均值μ的一个无偏估计量.

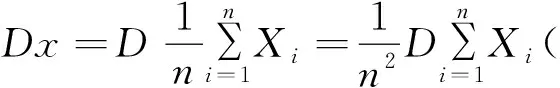
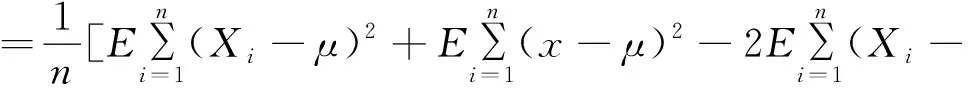
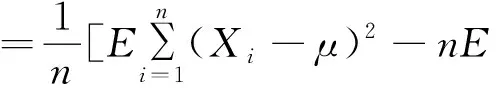
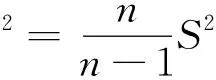
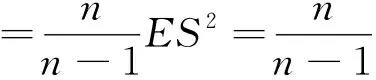
所以，S*2为σ2的一个无偏估计量.

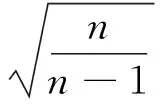
3.2 有效性

当总体参数不止有一种无偏估计时，某一种估计量的一切可能样本值的方差小的为有效性高，方差大的为有效性低.如：样本均值x、中位数Md、众数M0都是总体平均数μ的无偏估计量，但x的一切可能样本值的方差最小，所以x是总体平均数μ最有效的估计量.

3.3 一致性

当样本容量无限增大时，估计量的值能越来越接近它所估计的总体参数值，这种估计量是总体参数一致性估计量.如：样本均值x是总体平均数μ的一致性估计量，样本标准差s是总体标准差σ的一致性估计量.

通过上面的分析可见，上海教材里将样本的标准差

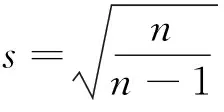
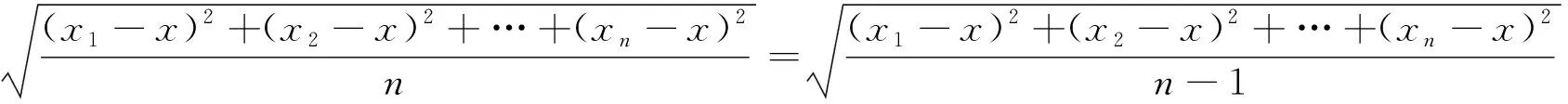
作为总体标准差的点估计值是合理的.

1 刘新平，刘存侠.教育统计与测评导论[M].北京：科学出版社.2012

2 王孝玲.教育统计学[M].上海：华东师范大学出版社.2003