基于空间自回归模型的广州市NDVI和NDBI与气温关系研究
许剑辉, 赵 怡, 肖明虹, 钟凯文, 阮惠华
(1.广州地理研究所,广州 510070; 2.广东省遥感与地理信息系统应用重点实验室,广州 510070;3.广东省地理空间信息技术与应用公共实验室,广州 510070; 4.中国科学院广州地球化学研究所,广州 510640; 5.中国科学院大学,北京 100049; 6.广西壮族自治区地理信息测绘院,柳州 545006; 7.广东省气象探测数据中心,广州 510080)
0 引言
在快速城镇化过程中,城市热环境质量日益恶化[1],城市热岛引起了社会的广泛关注。如何更好地监测、分析与评价城市热岛效应,已成为当前城市环境研究的热点问题[2-3]。城市热岛效应研究对城市环境质量改善和生态城市建设具有重要意义。
归一化植被指数(normalized difference vegetation index,NDVI)能较好地表征植被的生长过程,而且与气温、降水等具有紧密的联系[4-6],现已成为城市气候研究的重要指标[3],被广泛应用于城市植被覆盖监测、土地覆盖分类、地表温度、近地表气温(以下简称气温)和降水等研究[7-13]。作为量化城市热岛的重要指示器,地表温度和气温已被应用于城市热岛效应研究。许多学者采用不同的方法研究不同区域在不同季节下NDVI与地表温度和气温间的关系,结果表明NDVI与地表温度存在明显的负相关[14-16],而与气温间的关系则呈显著的空间异质性[4]。崔林丽等[17]采用时滞相关分析法研究华东及其周边地区NDVI对气温的时空响应特征,结果表明NDVI与气温在夏季和秋季相关性较高,冬季相关性最低; 历华等[18]指出单独使用NDVI定量研究城市热岛是不能满足要求的,城市建筑用地也是城市热岛研究的一个重要指标。一般用归一化建筑指数(normalized difference build-up index,NDBI)或建筑用地指数(index based-build-up index,IBI)提取建筑用地。相关学者研究了不同地区NDVI和NDBI与热岛分布间的关系,结果表明城市热岛与NDVI呈负相关,与NDBI呈正相关[19-21]。樊亚鹏等[22]以广州市为研究区域,分别采用IBI和NDVI分析了1990─2008年间广州市的热岛效应,结果发现广州市建筑用地与地表温度呈正相关,NDVI与地表温度呈负相关。
然而,上述研究仅利用相关性分析和普通回归方法分析NDVI和NDBI与地表温度和气温间的相关性,并没有考虑NDVI,NDBI和温度的空间自相关与空间异质性,也没有充分考虑地表温度和气温数据的空间信息,难以进一步挖掘NDVI和NDBI空间变异性对地表温度和气温的影响。鉴于此,本文结合MODIS NDVI数据,用Landsat8估计的NDBI和广州市264个气象观测站观测的2015年月平均气温,分别利用普通线性回归模型、空间滞后模型和空间误差模型在区域尺度上拟合NDVI和NDBI与气温的关系,定量分析城市NDVI和NDBI对气温时空格局的影响,为缓解广州市热岛效应、建设生态城市提供科学依据。
1 研究数据
1.1 气象数据
本文以广州市作为研究区。广州市位于广东省中南部、珠三角中北缘,地处亚热带沿海,属海洋性亚热带季风气候区,温暖多雨,年平均气温约20~22℃,7月份最热,月平均气温达28.7℃; 1月份最冷,月平均气温为9~16℃。气温数据采用广东省气象局提供的2015年1─12月自动气象观测站的近地表月平均气温。对这些气象观测站的气温数据进行质量检查,剔除存在明显异常的观测数据,得到264个站点的月平均近地表气温(图1)。选择冬(2015年1月)、春(2015年4月)、夏(2015年7月)、秋(2015年10月)4个季节的气温数据研究NDVI和NDBI与气温数据间的关系。
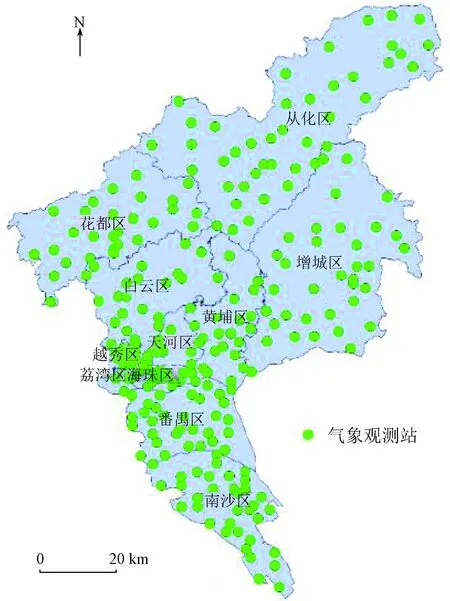
图1 研究区及气象观测站分布
1.2 MODIS NDVI数据
本文选取MODIS提供的月合成1 km空间分辨率植被指数(MOD13A3)数据产品作为NDVI数据源,对应的时间为2015年1─12月,数据下载于美国USGS数据中心(https: //lpdaac.usgs.gov/data_access/data_pool)。
利用NASA提供的MODIS Reprojection Tools(MRT)软件,将下载的MOD13A3数据进行数据格式转换和投影转换(投影坐标为WGS84 UTM Zone_49N),并利用研究区矢量边界进行影像裁剪,得到如图2所示的月合成NDVI数据。

(a) 1月 (b) 4月 (c) 7月 (d) 10月
图2研究区月NDVI数据
Fig.2MonthlyNDVIofstudyarea
从图2可以看出,从冬季到夏季,研究区NDVI指数随时间推移而增加; 从秋季到冬季,NDVI指数随时间推移而减少; 春、夏2季则NDVI变化比较大,表明春、夏2季植物生长旺盛。从整体上看,广州市主城区的NDVI指数较低,主要因为主城区以建筑物为主。
1.3 NDBI指数
NDBI指数是由查勇等[23]提出的基于Landsat TM影像构建的归一化建筑物指数,主要用来自动提取城市用地。采用美国地质调查局地球资源观测与科学中心(https: //espa.cr.usgs.gov/) 提供的2015年10月18日Landsat8 OLI遥感影像(空间分辨率为30 m,轨道号122/44,影像无云,数据质量好)计算NDBI指数,即
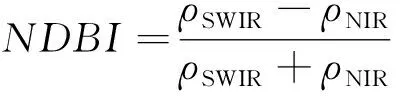
(1)
式中ρSWIR和ρNIR分别为Landsat8 OLI第6和第5波段的光谱反射率。
由于MODIS NDVI的空间分辨率为1 km,为了让NDBI的空间分辨率与NDVI的空间分辨率保持一致,对高空间分辨率的NDBI采用算术平均的方法得到空间分辨率为1 km的NDBI[24]。首先,利用ArcGIS的空间分析模块,对空间分辨率为30 m的NDBI进行最邻近插值,得到空间分辨率为25 m的NDBI指数; 再采用ArcGIS的聚合分析功能,使用像元系数40取平均值的方式对空间分辨率为25 m的NDBI栅格图像进行聚合,获取与NDVI数据像元大小一致、投影相同的栅格数据(图3)。
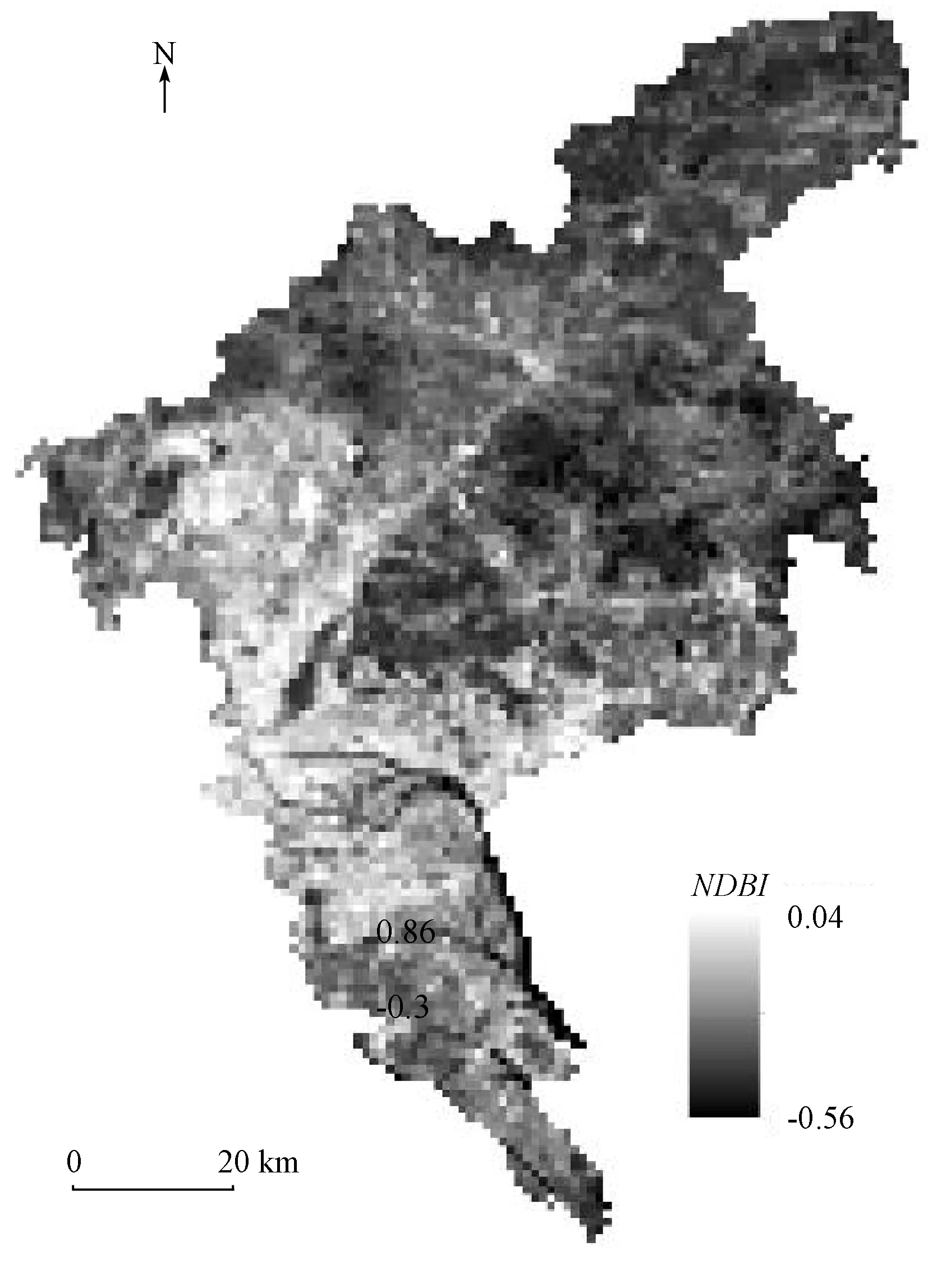
图3 研究区NDBI数据
此外,由于研究区1 a内城市建筑用地变化不大,所以将计算的2015年10月18日NDBI指数视为2015年全年的平均NDBI指数(图3),显示了当年研究区的城市建设用地情况。从图3可以看出,该区建设用地主要集中在广州市主城区,郊区的NDBI指数比较低(为负数),与图2具有类似的分析结果。
2 研究方法
2.1 空间自回归模型
以月平均近地表气温为因变量,以NDBI和NDVI为自变量,首先分析气温与NDVI和NDBI之间的相关关系,然后分别采用普通线性回归模型、空间自回归模型(空间滞后模型、空间误差模型和空间杜宾模型)对不同季节的近地表气温及其影响因子进行建模分析。
Anselin[25]提出的空间自回归模型为
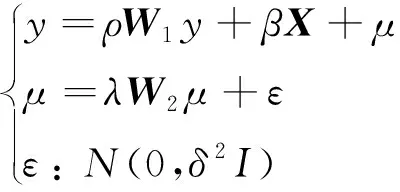
(2)
式中:y为因变量,指月平均近地表气温;X为自变量,表示与近地表气温相关的影响因素(包括NDBI和NDVI);β为自变量的回归系数;μ为随机误差项;ε为服从均值为0、方差为δ2的随机误差;W1和W2分别为因变量自身与残差空间趋势的权重矩阵;ρ为空间滞后项W1y的系数;λ为空间误差项的回归系数。
当式(1)参数向量的不同向量设置为0时,可以产生4种不同的空间模型结构,本文只考虑其中的3种,即
1)当ρ=0,λ=0时,为普通线性回归模型(ordinary linear regression,OLS)。该模型一般假设观测值相互独立不受其他因素影响,不考虑区域间的空间差异性。
2)当ρ≠0,λ=0时,为空间滞后模型(spatial lag model,SLM)。该模型考虑了因变量的空间相关性,即某一空间区域的因变量不仅与同一区域的自变量有关,而且与相邻区域的因变量有关。
3)当ρ=0,λ≠0时,为空间误差模型(spatial error model,SEM)。该模型不考虑因变量的空间相关性,只考虑了自变量的空间自相关性,即某一空间区域的因变量与同一区域的自变量、相邻区域的自变量和因变量有关。
采用赤池信息量准则(Akaike information criterion,AIC)信息指标[26](一种衡量统计模型拟合优良性的标准)评价空间自回归模型的拟合精度,并利用莫兰指数(Moran index,Moran’s I)对回归模型误差项进行空间自相关分析。一般认为,较低的AIC表明模型的模拟效果更好; 当2个模型之间的AIC值相差大于3时,具有较小AIC值的模型对数据的模拟效果更好。回归模型残差的空间自相关分析也可作为评价回归模型拟合效果的一个指标。Moran’s I值接近0表示回归模型的残差不存在空间自相关性,回归模型拟合效果较好; Moran’s I值大于或者小于0,表示回归模型的残差仍存在明显的空间自相关性,回归模型拟合效果较差。
2.2 空间权重的选择
一般地,空间权重矩阵可以通过二元邻居和距离函数进行计算。由于本文采用的近地表气温数据是气象站点数据,因此选择空间距离函数来计算空间权重矩阵。经过比较分析,最终确定距离阈值为12 km。
3 结果与分析
3.1 NDVI和NDBI与近地表气温间的关系
为研究NDVI和NDBI与近地表气温间的关系,研究区所有自动气象观测站观测的不同季节的月平均近地表气温与NDVI和NDBI的散点图如图4和5所示。

(a) 1月 (b) 4月

(c) 7月(d) 10月
图4不同季节近地表气温与NDVI散点图
Fig.4ScatterplotsofairtemperatureandNDVIindifferentseasons
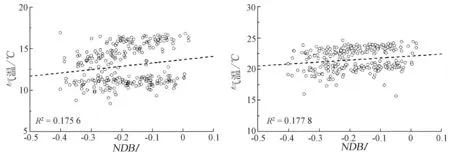
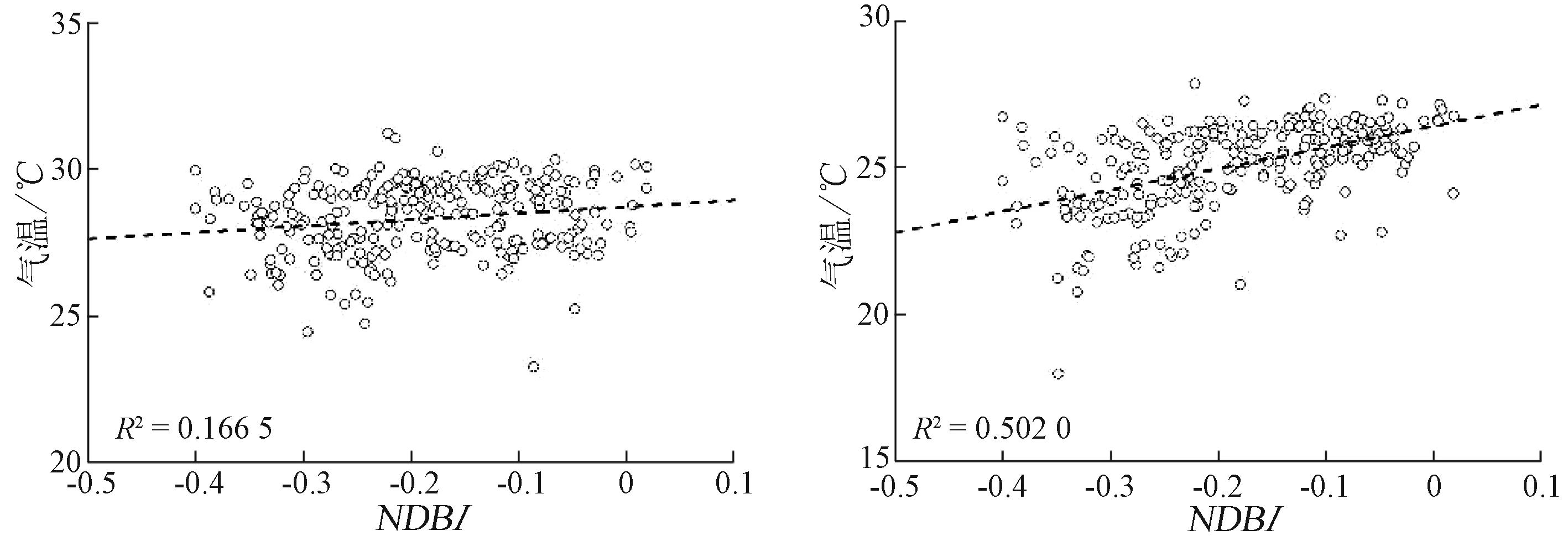
从图4可以看出,4个季节的NDVI与近地表气温间存在显著的负相关关系,相关系数随时间的推移而变化,冬季的相关系数最低,与崔林丽等[17]的研究结果类似。与之相反的是,NDBI与近地表气温间存在正相关关系(图5)。从图5可以看出,冬、春、夏3个季节的正相关系数相差不大,秋季NDBI与近地表气温间存在显著的正相关关系,相关系数达到了0.502。这可能与对NDBI与不同季节近地表气温进行比较时只用了2015年10月18日这1个时相的NDBI有关。另外,1 km空间分辨率的NDBI是通过将30 m空间分辨率的NDBI经过插值、聚合分析得到的,这也会引入一些误差。从图4和5可以发现,冬季和春季的NDVI和NDBI与近地表气温间的相关性存在2个非常明显的区间,形成一高一低聚集的现象。在冬季(图4(a)和图5(a))近地表气温较低时,NDVI和NDBI与近地表气温间的相关系数比较小; 在春季(图4(b)和图5(b))近地表气温较高时,NDVI和NDBI与近地表气温间的相关系数显著增加。近地表气温较低的气象观测站主要集中在广州市主城区、花都区以及南沙区; 与之相反的是,番禺区、增城区和从化区的近地表气温比较高。到了春季,虽然分区还存在,但是它们之间相关系数的差异缩小了,比较接近。近地表气温的气象观测站聚集的区域发生了改变,近地表气温较低的气象观测站主要集中在广州市主城区、花都区以及增城区。到了夏季和秋季,分区不复存在,近地表气温较高的气象观测站主要聚集在荔湾区、越秀区、海珠区、番禺区以及南沙区。从图4中也可以看出,NDVI越大,植被生长越茂盛,近地表气温越低。这表明通过植树造林,提高城市绿化率可以起到降温的作用。从图5中则可以看出,NDBI越大,城市建筑用地面积越大,近地表气温越高。这表明城市的扩张(建筑物增加、不透水面的增加和植被的减少)提升了城市整体的气温,从而出现城市“热岛”现象。
(a) 1月 (b) 4月
(c) 7月 (d) 10月
图5不同季节的近地表气温与NDBI散点图
Fig.5ScatterplotsofairtemperatureandNDBIindifferentseasons
3.2 空间自回归模型比较
利用R语言的spdep函数包建立了不同季节的近地表气温与NDVI和NDBI间的空间自回归模型: OLS,SLM和SEM。空间自回归模型的分析及检验结果见表1─4。
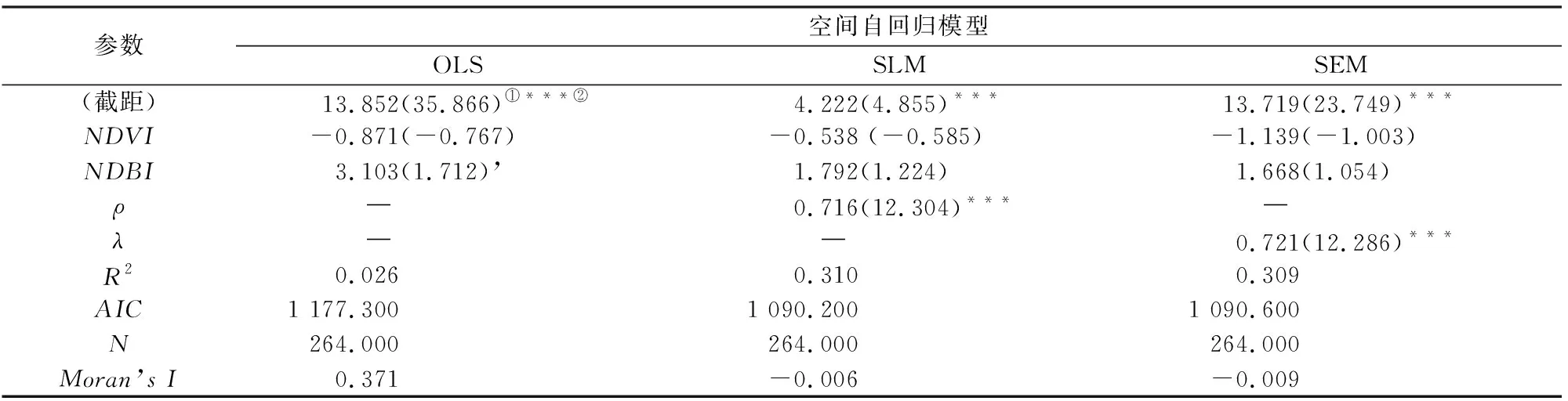
表1 1月份近地表气温3种空间自回归模型参数Tab.1 Parameters of three different spatial autoregressive models for air temperature in January
①括号里的值表示显著性检验t或者z统计值; ②***表示显著性水平P<0.000; **表示P<0.001; *表示P<0.01; .表示P<0.05; ’表示P<0.1。下表中含义相同。

表2 4月近地表气温3种空间自回归模型参数Tab.2 Parameters of three different spatial autoregressive models for air temperature in April

表3 7月近地表气温3种空间自回归模型参数Tab.3 Parameters of three different spatial autoregressive models for air temperature in July
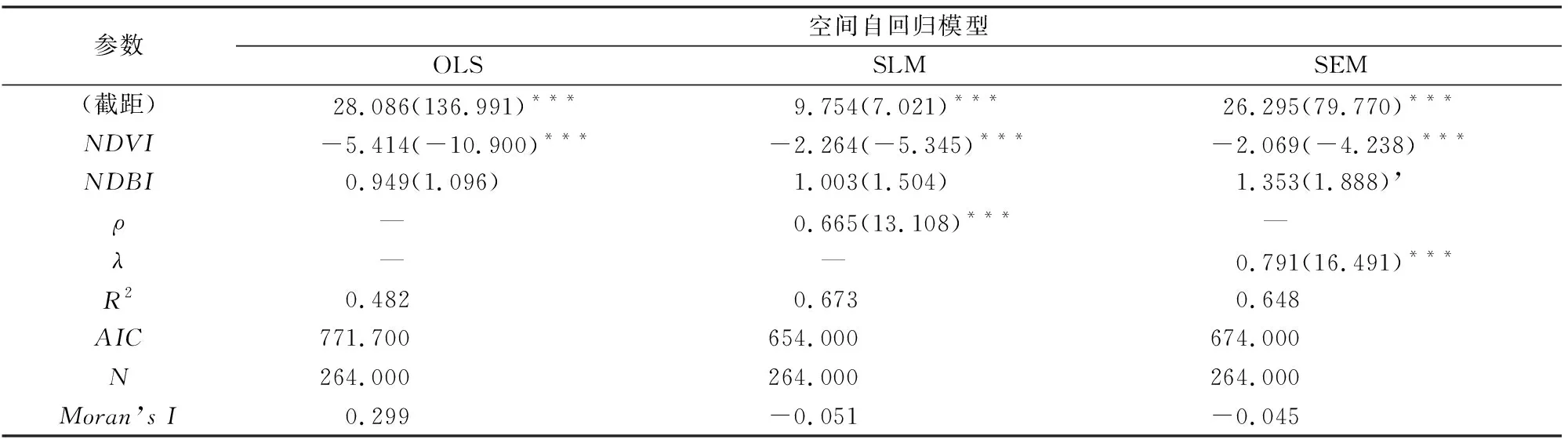
表4 10月近地表气温3种空间自回归模型参数Tab.4 Parameters of three different spatial autoregressive models for air temperature in October
从表1中可以看出,OLS中自变量NDVI的系数为负数,NDBI的系数为正数,表明冬季近地表气温与NDVI存在负的相关性,与NDBI存在正的相关性,即地区的植被生长越茂盛,建筑用地越少,近地表气温越低。然而,OLS的R2仅为0.026,拟合度较差; OLS残差的Moran’sI高达0.371,具有很强的空间自相关。这进一步说明,不考虑空间相关的OLS不能有效地解释变量之间的关系。
SLM中R2为0.310,明显高于OLS的0.026;AIC为1 090.2,小于OLS的AIC,说明SLM的拟合效果优于OLS。另外,SLM中ρ为正且显著,表明因变量之间具有很强的空间自相关。Moran’sI接近0,表明SLM的残差在空间上不再聚集。SEM中λ为正且显著,说明模型误差具有很强的空间依赖。SLM的检验参数与SEM检验参数非常接近,总体上,SLM略优于SEM。
在SLM中,从冬季到秋季,NDVI的回归系数分别为-0.538(表1)、-1.783(表2)、-1.397(表3)和-2.264(表4),总体上随季节减少,而NDBI的回归系数从1.792(表1)减少到0.265(表3),然后又增加到1.003(表4),但整体上还是呈现出一种随季节减少的趋势。这表明从冬季到秋季,NDVI对近地表气温的影响逐渐增大,而NDBI对近地表气温的影响逐渐减少。这是因为从冬季到秋季植物处在生长过程,NDVI值在不断增加,到秋季植物茂盛时NDVI值达到最大,而城市建设用地基本变化不大,在这个时间段内,植被对近地表气温的影响大于城市建设用地。在冬季,由于部分植被绿叶变黄掉落,NDVI值达到最小,此时建设用地对近地表气温的影响占主导地位。
从表1─4可以看出,SLM的空间自回归系数ρ显著,广州市各气象站点不同季节的近地表气温不仅受到NDVI和NDBI的影响,还与相邻气象站点的近地表气温显著相关。从表1─表4也可以发现,不同季节的SLM的空间自回归系数ρ变化不大,基本都在0.66左右,这说明了每个气象站点的气温都受到相邻气象站点气温较恒定的显著正影响。
表2─4表示SLM和SEM的拟合效果都远优于OLS; 回归模型的决定系数R2最小值为0.356(表3),最大值为0.673(表4)。春季近地表气温与NDVI和NDBI的SLM的R2,AIC以及回归模型残差的Moran’sI指数都优于SEM。夏季时,SEM的R2和AIC优于SLM,但是其模型残差的Moran’sI大于SLM,Moran’sI为-0.006表明SLM残差是相互独立,在空间上不聚集。冬季与夏季相反,尽管SLM残差的Moran’sI的绝对值略大于SEM,但是SLM的R2和AIC远优于SEM。因此,从整体上看,SLM的拟合效果略优于SEM。利用SLM来分析不同季节近地表气温与NDVI和NDBI间的空间关系更合理。
4 结论
本文结合2015年月均站点近地表气温、MOD13A3的NDVI以及用Landsat8 OLI提取的NDBI等数据,采用相关性分析以及空间自回归模型,研究了广州地区不同季节近地表气温与NDVI和NDBI之间的相关关系,得到以下结论:
1)从冬季到秋季,NDVI指数随时间增加; 从秋季到冬季,NDVI指数随时间减少。4个季节的NDVI与近地表气温间存在显著的负相关关系,NDBI与近地表气温间存在正相关关系。
2)4个季节的近地表气温与NDVI和NDBI的OLS的残差的Moran’sI都大于等于0.299,表明普通回归模型的残差存在显著的空间自相关性,说明了OLS并没有考虑近地表气温本身以及与NDVI和NDBI间的空间自相关性的影响。因此,需采用空间自回归模型来分析近地表气温与NDVI和NDBI之间的相关关系。
3)分别建立不同季节近地表气温与NDVI和NDBI间的SLM与SEM。经过SLM与SEM回归后,回归模型的R2有了很大的提高,AIC减少较多,说明SLM与SEM的拟合度优于普通回归模型。SLM与SEM的残差的Moran’sI接近0,表明残差的空间自相关性已消失。因此,SLM与SEM都能较好地解释不同季节近地表气温与NDVI和NDBI间的相关关系。通过比较分析R2,AIC以及回归模型残差的Moran’sI,发现整体上SLM的拟合效果略优于SEM。
4)在SLM中,NDVI对近地表气温的影响随着季节逐渐增大,而NDBI对近地表气温的影响随着季节逐渐减少。SLM的空间自回归系数ρ为正数且显著,表明近地表气温受到相邻气象站点的近地表气温显著的正影响。
本文仅分析了NDVI和NDBI与气温的回归关系; 实际上,除了NDVI与NDBI外,其他很多因素都直接影响气温的变化,如降雨、地形和风速等。未来的研究可以将这些因素融合到空间自回归模型中,以获取更为客观合理的分析结果。此外,本文在时间尺度上仅利用了2015年4个月的数据分析气温与NDVI和NDBI间的关系,尚未将长时间序列的数据纳入研究,今后需利用长时间序列数据更加深入地分析、探讨城市气温的时空变化特征。
参考文献(References):
[1] 肖荣波,欧阳志云,李伟峰,等.城市热岛的生态环境效应[J].生态学报,2005,25(8):2055-2060.
Xiao R B,Ouyang Z Y,Li W F,et al.A review of the eco-environmental consequences of urban heat islands[J].Acta Ecologica Sinica,2005,25(8):2055-2060.
[2] 岳文泽,徐丽华.城市土地利用类型及格局的热环境效应研究——以上海市中心城区为例[J].地理科学,2007,27(2):243-248.
Yue W Z,Xu L H.Thermal environment effect of urban land use type and pattern:A case study of central area of Shanghai City[J].Scientia Geographica Sinica,2007,27(2):243-248.
[3] Yuan F,Bauer M E.Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery[J].Remote Sensing of Environment,2007,106(3):375-386.
[4] 韩 雅,朱文博,李双成.基于GWR模型的中国NDVI与气候因子的相关分析[J].北京大学学报(自然科学版),2016,52(6):1125-1133.
Han Y,Zhu W B,Li S C.Modelling relationship between NDVI and climatic factors in China using geographically weighted regression[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2016,52(6):1125-1133.
[5] 沈 斌,房世波,余卫国.NDVI与气候因子关系在不同时间尺度上的结果差异[J].遥感学报,2016,20(3):481-490.
Shen B,Fang S B,Yu W G.Different correlations between NDVI and meteorological factors at temporal-time scales[J].Journal of Remote Sensing,2016,20(3):481-490.
[6] 仙 巍,邵怀勇.长江上游安宁河流域植被生长变化对气候条件的响应[J].国土资源遥感,2015,27(3):108-113.doi:10.6046/gtzyyg.2015.03.18.
Xian W,Shao H Y.Responses of vegetation changes to climatic variations in Anning River Basin of upper Yangtze River Region[J].Remote Sensing for Land and Resources,2015,27(3):108-113.doi:10.6046/gtzyyg.2015.03.18.
[7] 殷 刚,孟现勇,王 浩,等.1982—2012年中亚地区植被时空变化特征及其与气候变化的相关分析[J].生态学报,2017,37(9):3149-3163.
Yin G,Meng X Y,Wang H,et al.Spatial-temporal variation of vegetation and its correlation with climate change in Central Asia during the period of 1982—2012[J].Acta Ecologica Sinca,2017,37(9):3149-3163.
[8] 梁守真,禹定峰,王 猛,等.应用遥感时序数据研究植被变化与气候因子的关系——以环渤海地区为例[J].国土资源遥感,2015,27(3):114-121.doi:10.6046/gtzyyg.2015.03.19.
Liang S Z,Yu D F,Wang M,et al.Application of remote sensing time-series data to investigate the relationship between vegetation change and climatic factors:A case study of Circum-Bohai Sea area[J].Remote Sensing for Land and Resources,2015,27(3):114-121.doi:10.6046/gtzyyg.2015.03.19.
[9] 孟 丹,李小娟,宫辉力,等.京津冀地区NDVI变化及气候因子驱动分析[J].地球信息科学学报,2015,17(8):1001-1007.
Meng D,Li X J,Gong H L,et al.Analysis of spatial-temporal change of NDVI and its climatic driving factors in Beijing-Tianjin-Hebei metropolis circle from 2001 to 2013[J].Journal of Geo-Information Science,2015,17(8):1001-1007.
[10] Li J Z,Zheng J G.Study on the relationship between urban surface temperature and vegetation index in Xuchang City[J].Applied Mechanics and Materials,2013,321-324:2496-2500.
[11] Huang C D,Ye X Y.Spatial modeling of urban vegetation and land surface temperature:A case study of Beijing[J].Sustainability,2015,7(7):9478-9504.
[12] Walther G R,Post E,Convey P,et al.Ecological responses to recent climate change[J].Nature,2002,416(6879):389-395.
[13] Liu J H,Wu J J,Wu Z T,et al.Response of NDVI dynamics to precipitation in the Beijing-Tianjin sandstorm source region[J].International Journal of Remote Sensing,2013,34(15):5331-5350.
[14] 侯光雷,张洪岩,王野乔,等.基于MODIS数据的吉林省中部地表温度反演及空间分布研究[J].地理科学,2010,30(3):421-427.
Hou G L,Zhang H Y,Wang Y Q,et al.Retrieval and spatial distribution of land surface temperature in the middle part of Jilin Province based on MODIS data[J].Scientia Geographica Sinica,2010,30(3):421-427.
[15] 贾虎军,杨武年,周 丹,等.基于MODIS地表温度和归一化植被指数的生态环境变化分析[J].遥感信息,2014,29(3):44-49.
Jia H J,Yang W N,Zhou D,et al.Analysis of the ecological environment changes in land surface temperature and NDVI based on MODIS remote sensing data[J].Remote Sensing Information,2014,29(3):44-49.
[16] Kumar D,Shekhar S.Statistical analysis of land surface temperature-vegetation indexes relationship through thermal remote sensing[J].Ecotoxicology and Environmental Safety,2015,121:39-44.
[17] 崔林丽,史 军.中国华东及其周边地区NDVI对气温和降水的季节响应[J].资源科学,2012,34(1):81-90.
Cui L L,Shi J.Characteristics of seasonal response of NDVI to variations in temperature and precipitation in east China and its surrounding areas[J].Resources Science,2012,34(1):81-90.
[18] 历 华,柳钦火,邹 杰.基于MODIS数据的长株潭地区NDBI和NDVI与地表温度的关系研究[J].地理科学,2009,29(2):262-267.
Li H,Liu Q H,Zou J.Relationships of LST to NDBI and NDVI in Changsha-Zhuzhou-Xiangtan Area based on MODIS data[J].Scientia Geographica Sinica,2009,29(2):262-267.
[19] 宋瑞祥,张庆国,孟庆岩,等.基于Landsat8 OLI数据的合肥市热岛时空特征分析[J].安徽农业大学学报,2016,43(3):474-480.
Song R X,Zhang Q G,Meng Q Y,et al.Landsat8 OLI data-based analysis of spatial-temporal characteristics of heat island in Hefei[J].Journal of Anhui Agricultural University,2016,43(3):474-480.
[20] 薛晓娟,孟庆岩,王春梅,等.北京市热岛效应时空变化的HJ-1B监测分析[J].地球信息科学学报,2012,14(4):474-480.
Xue X J,Meng Q Y,Wang C M,et al.Monitoring spatio-temporal changes of heat island effect in Beijing based on HJ-1B[J].Journal of Geo-Information Science,2012,14(4):474-480.
[21] Grover A,Singh R B.Analysis of urban heat island(UHI) in relation to normalized difference vegetation index(NDVI):A comparative study of Delhi and Mumbai[J].Environments,2015,2(2):125-138.
[22] 樊亚鹏,徐涵秋,李 乐,等.广州市城市扩展及其城市热岛效应分析[J].遥感信息,2014,29(1):23-29.
Fan Y P,Xu H Q,Li L,et al.Analysis of urban expansion and urban heat island effect in Guangzhou City[J].Remote Sensing Information,2014,29(1):23-29.
[23] 查 勇,倪绍祥,杨 山.一种利用TM图像自动提取城镇用地信息的有效方法[J].遥感学报,2003,7(1):37-40.
Zha Y,Ni S X,Yang S.An effective approach to automatically extract urban land-use from TM imagery[J].Journal of Remote Sensing,2003,7(1):37-40.
[24] Tan B,Hu J N,Zhang P,et al.Validation of moderate resolution imaging spectroradiometer leaf area index product in croplands of Alpilles,France[J].Journal of Geophysical Research,2005,110(D1):D01107.
[25] Anselin L.Spatial Econometrics:Methods and Models[M].Dordrecht: Kluwer Academic Publishers,1988.
[26] Akaike H.Information theory and an extension of the maximum likelihood principle[M]//Petrov B N,Csáki F.Second International Symposium on Information Theory.Budapest:Académiai Kiadó,1973:267-281.
——以关中地区为例

