USB插入成功率的影响因素研究

李子敬 吕志浩 张建新

摘要：USB接口有时候会插反，然而有时其实是插正的，但是因为插了几下没插进去而以为自己插反了，这就使得成功插入需要的次数不确定。文章研究了影响插入成功率的因素。采用变异系数法确定权重，构建综合评价模型，得出各影响因素的排行。之后运用方差分析的方法验证了之前评价模型的结论，并且进一步分析各因子不同取值的影响。

关键词：USB设备插入成功率；变异系数法；单因子方差分析；均值的多重比较

USB设备的插头有正反之分，这造成了一个有趣的现象：若是在将其插入USB接口时，未能成功插入，就会选择换一个方向插入[1]。而有时选择的插入方向其实是对的，但也没插入进去，便会以为选择了错误的方向。再换方向插入USB接口，那用错误的方向自然是插不进去的。这就导致我们有时需要尝试多次才能成功插入USB接口，这让人感到心烦，同时也磨损了设备[2]。本文研究了影响插入成功率的因素，考虑使用年限、插口类型、插入设备类型、插入方式、品牌和容量大小这6个因素，并给出这几个因素对插入成功率影响的排名和最优的配比。

1 实证研究

1.1对u盘进行评价分析

1.1.1变异系数法

首先运用变异系数法将实际值和理论值共同构造U盘评价指标体系，特别说明，这里的权重指的是各个变量对于一个U盘插入成功率的影响起多大的作用[3-4]。U盘成功插入所需次数的影响因素权重体系如表1所示。

计算过程如下：

（1）先根据各个类型U盘的指标数据，分别计算这些盘各个指标的平均数和标准差。

（2）根据均值和标准差计算变异系数。

即这些U盘的品牌的变异系数：U盘的容量的变异系数：其他类推。

（3）将各项指标的变异系数加总：0.12 2+0.117+0.19 6+0.18 4+0. 5+0.183 =1.3 02

（4）计算构成评价体系的这6个指标的权重。

U盘的品牌的权重：

U盘的容量的权重：

其他指标的权重都以此类推。计算的结果如表1所示。

1.1.2方差分析

（1）方差齐性检验：在此选用Bartlett检验。由R软件的分析得出结果如表2所示。

在上表中，由于尸值（0.464，0.752，0.232，0.620，0.149，0.339>0.05，故接受原假设，认为各处理组的数据满足方差齐性的要求。因此，该问题可以使用方差分析的方法进行分析。

（2）方差分析实验：由R软件进行方差分析，结果如表3所示。

品牌、容量、插口类型、插入设备类型、使用年限和插入方式的方差分析结果表明，不同的插口类型、插入设备类型、使用年限和插入方式对应的USB设备插入成功需要次数存在显著差异（P<0.05），而不同的品牌和容量对应的USB设备插入成功需要次数不存在显著差异（P>0.05）。F值为组间均方与组内均方的比值，表示不同分组间样本均数的差别，其值越大，说明不同分组间的差异越明显。不同因子的方差分析F值差异较大，其中容量的F值最小，为1.451，插入方式的F值最大，为29.91，说明各因子对USB设备插入成功需要次数的影响存在差异性。

（3）均值的多重比较：进行方差分析后发现各效应的均值之间有显著差异，我们知道某些均值彼此不同，但也要知道是哪些均值彼此不同，在此，我们选用多重t检验方法。

由R软件进行多重t检验并且作出箱图，来对每一个因子进行进一步分析。

①插口类型

xl：套盖型

x2：开放型

x3：芯片型

多重t检验结果如表4所示，插入成功所需次数的箱图如图1所示。x2与x1之间的P=0.009<0.05，所以x2与x1所用的次数显著不同，并比x1多。x2与x3虽然在P=0.05的水平下没有显著不同，但尸=0.082也较小，所以结合来看，x2比x1和x3插入的次数需要得更多一些，即是说在x2的条件下，USB设备不易插入。而x1与x2之间的尸值为0.317>0.05，它们没有显著不同。可以看出，开放型的USB插头较难插入，而套盖型的插头和芯片型插头较易插入。

②插入设备类型

x1：台式机箱；x2：笔记本电脑；x3：落地式电视；x4：挂壁式电视。

多重t检验结果如表5所示，插入成功所需次数的箱图如图2所示。x1与x2，x3，x4的P值都为0.000<0.05，因此，在x1条件下USB设备插入所需次数与x1，x2，x3条件下显著不同，并比他们小。而x2与x3的尸值为0.161>0.05，因此认为，x2与x3的条件并没显著差异。而x4与x2和x3的尸值都为0.000<0.05，所以结合箱图，我们认为，x4条件下的插入所需次数显著比x2和x3条件下大。总结来说，台式机箱的接口USB设备最易插入；笔记本电脑和落地式电视其次容易插入：挂壁式电视最难插入，这也符合直观的经验，即挂壁式电视需要从比较小的角度探到其背面，再进行插入尝试。

⑧使用年限的不同

x1： 0-1年；x2： 1-3年；x3： 3-5年；x4：5年以上。

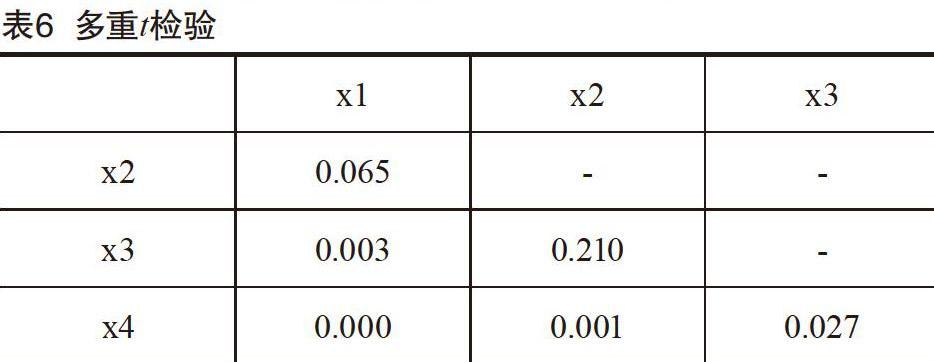
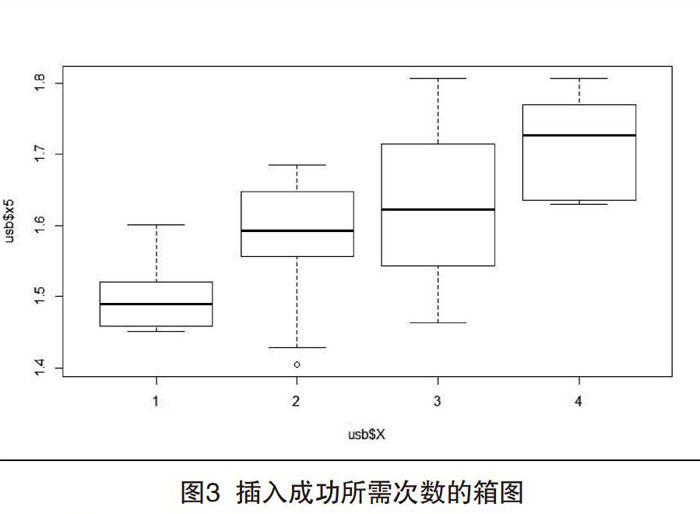
多重t检验结果如表6所示，插入成功所需次数的箱图如图3所示。xl与x2的尸值为0.065>0.05，所以xl和x2条件下的USB设备插入所需次数没有显著差异。而xl与x3和x4的尸值分别为0.003和0.000，它们都小于0.005，结合箱图，我们认为，x1条件下的所需次数比x3和x4条件下小。而x2与x3的尸值为0.210>0.05，所以x2和x3条件下的所需次数没有显著差异。最后x4与x1、x1和x3的尸值0.000、0.001和0.027，都小于0.05的置信水平，所以x4條件下的所需次数显著较大。总结来说，虽然x1与x2、x2与x3条件下的插入难度没有显著不同，但是x1与x3，x2与x4，x3与x4条件下插入难度都显著不同，且都满足使用年限越长，越难插入的特点。因此，我们得出USB设备使用年限越长，越难插入的结论。

④插入方式的不同

x1：事先未检查USB插头的正反，并且在插入过程中也不检查插头的正反。

x2：事先未检查USB插头的正反，在插入失败后检查插头的正反。

x3：事先检查USB插头的正反，在插入失败后不检查插头的正反。

x4：事先检查USB插头的正反，并且在插入失败后检查插头的正反。

多重t检验结果如表7所示，插入成功所需次数的箱图如图4所示。x1与x2，x3和x4的尸值都为0.000<0.05，因此在x1条件下USB设备插入所需次数与x1，x2，x3条件下显著不同，并比他们大。而x2和x3的尸值为0.029<0.05，结合箱图，我们认为，x2条件下的需要次数比x3显著大；x2与x4的尸值为0.140>0.05，故我们认为它们没有显著差异。最后x4与x3的尸值为0.452，所以它们的所需次数无显著差异。总结的说，在x1的插入方式下，所需的次数最多，其次是x3的插入方式，x2的插入方式需要次数最少。而x4的插入方式肯定比x1的插入方式更優，并且与x2和x3的插入方式都差不多。因此，不论什么样的检查形式，只要对USB设备的插头进行检查正反，USB设备就能更容易地插入。

（4）由方差分析得出的排名：我们利用glm语句得出显著变量（插口类型、插入设备类型、使用年限和插入方式）相应的估计。如表8所示，我们能得出各因子的排名，即：使用年限>插口类型>插入设备类型>插入方式。该结果与变异系数法的结论完全吻合[5]。

2 结语

综合变异系数法和方差分析法的结论，我们可以得出6个指标的排行如下：（1）使用年限：（2）插口类型；（3）插入设备类型；（4）插入方式：（5）品牌：（6）容量大小。

此外我们还可以得出：（1）开放型的USB插头较难插入。（2）台式机箱的接口USB设备最易插入。（3） USB设备使用年限越长，越难插入。（4）不论什么样的检查形式，只要对USB设备的插头进行检查正反，USB设备就能更容易地插入。

我们这次研究的创新点是基于USB具有以下5个条件进行的：（1）速度快。（2）设备安装和配置容易。（3）易于安装。（4）使用灵活。（5）产品成本低[6]。研究结论对于厂家生产U盘以及消费者购买U盘有指导性建议。

[参考文献]

[1]冉自博基于u盘高速串行数据记录器设计[D].太原：中北大学，2014

[2]汤银才R语言与统计分析[M].北京：高等教育出版社，2008

[3]杨小勇方差分析法浅析——单因素的方差分析[J].实验科学与技术，2013 （1）：41-43.

[4]宋喜芳，李建平，胡希远.模型选择信息量准则AIC及其在方差分析中的应用[J].西北农林科技大学学报（自然科学版），2009 （2）：88-92

[5]RODIN E.Mathematical and computer modelling[J].Mathematical and Computer Modelling， 1989（12）： 1-2.

[6]VOATES V， FAROOQUE M， KLAVANS R，et al.Technological forecasting&social; change[J].Technological Forecasting&SocialChange;，2001 （1）：1-17.