一种基于直线检测的图像畸变校正方法

李威威 千博

摘要：文章介绍并利用具有图像径向和切向畸变的Brown模型及其像平面的直线不变性，分析了启发式算法之一的模拟退火算法，对Brown模型的几个参数变量进行求解最优解，选择Canny算子进行边缘检测，之后经过噪声抑制处理后进行霍夫变换得到直线检测的结果，然后从检测的直线中找出拟合最长的直线，以直线的长度作为模拟退火算法的能量函数，经过多次迭代后趋于稳定，输出最优解。本方法的精度控制在2 pixels范围内，通过对实际畸变图像的校正，验证了该直线检测几何校正方法的准确性。

关键词：畸变校正；直线检测；模拟退火算法；Brown模型

图像的畸变是由于光学镜头在设计、装配等的过程中产生的，存在光学系统的环境中，都会存在一定的畸变，畸变是由于镜头随着镜头径向的曲率不同，产生像差，使得原始图像中的直线弯曲，可能会凹陷或者凸显，根据畸变距离与理想的距离偏大或偏小，称为桶形畸变和枕形畸变[1]。

摄像机的标定是图像畸变校正的关键问题，标定主要是利用高精度的具有标记的模板作为空间参考，通过建立标定板与摄像机的三维坐标转换关系来确定摄像机的内外参数。由此可见参数的估计至关重要，而参数好坏的评定标准的选择则是重中之重。传统的标定方法有Tsai[2]的两步法相机标定，2hang[3]的棋盘标定法，他们都是经过测量进行的，而目前的一些非测量方法也得到了广泛的研究，主要是根据直线特征[4]的不变性进行的。本文也是根据非测量、直线特征来进行完成标定的。首先选用Brown模型[5]作为畸变模型是考虑了不同方向上的畸变参数，经过分解将畸变因素分解成径向和切向两个方向，更能准确地表示实际的畸变情况。本文主要利用Brown模型的根本思想：实际物理空间在理想成像系统中的直线不变性[6]，来进行作为参数优劣的标准。

1 图像畸变模型

由上可知，Brown模型具有较好的匹配性，该模型的数学表达式是：

（xc，yc）为径向畸变中心点，（xd，yd）为畸变图像像素点坐标，（xu，yu）为原图像像素点坐标，Knn为径向畸变n阶系数，Pn。为切向畸变n阶系数：r为畸变像素点到中心点的距离，在本文中，只考虑最高2阶的畸变模型情况，故需要使用的参数是xc，yc，K2，P1，P2。

2 畸变校正原理及流程

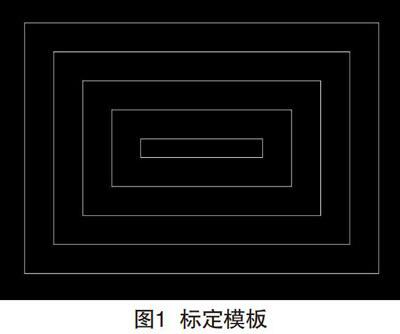
首先利用如图l所示的标定板，包含若干圈回字格，关于中心对称，内圈的使用相机拍摄图片得到的畸变图像如图2所示。利用电脑屏幕作为基板，因为电脑屏幕具有很高的像素精度，这样避免了打印标定板造成的误差。本文主要通过根据上述，Brown模型的基本思想：实际物理空间在理想成像系统中的直线不变性。由于标定板的特性是内圈直线短，外圈直线长，当存在畸变时，会使直线变弯曲，并且越是往外畸变的情况越是大，所以对于畸变的参数来说，检测到的直线越长，说明参数越是最优。至于如何检测图像中的直线以及直线的长度，本文首先进行边缘检测，之后采用霍夫变换进行处理，得到直线的信息和最长直线的位置与长度，以此作为衡量的标准，进行数据参数的优化。

2.1利用边缘提取获得图像曲线

边缘检测的方法有许多种，区别是算子的不同，主要分为一阶微分算子和二阶微分算子，一阶微分算子有：Sobel算子对灰度渐变和噪声较多的图像处理效果较好，对边缘定位不是很准确，图像的边缘不止一个像素。Roberts算子的边缘提取较宽，故精度不够。Prewitt算子对噪声不敏感，能够很好地过滤噪声，缺点是检测的边缘较宽，精度也不够。Canny算子也具有对噪声不敏感的特性，对边缘的强弱能够进行区分，对弱边缘的取舍具有较好的处理，能够检测出更准确的真正的边缘[7]。二阶微分算子有：Laplacian算子对图像的要求较高，如果存在噪声监测的结果会大受影响，故很少使用该算子进行边缘检测。

本文进行边缘检测的图像对像是边界分明的回字格，噪声不多，但是对精度的要求较高，综合考虑本文采用Canny算子进行边缘信息的提取。

Canny算子首先用高斯滤波器进行平滑图像，尽量减少图像中的噪声，避免对检测精度造成的影响。其次进行边缘的强化，采用一阶偏导的有限差分来计算梯度幅值和方向，在这一阶段，得到的梯度值并不能作为边缘的判断标准，因为进行了图像的增强，所以还要进行非极大值抑制，去除大量的非边缘的干扰点。最后利用两个阂值来连接边缘，这两个阂值的设置直接影响着检测的精度。

2.2利用霍夫变换获得直线的长度

理想图像中的直线在畸变图像中是曲线，利用己知的Brown系数进行畸变校正处理后，进行检测校正后图像中直线的长度，通过比较长度可以作为畸变校正系数选定优劣的标准。本文检测直线长度的方法是霍夫变换。

霍夫变换本质是坐标变换，在直角坐标系x-y中，直线方程y=kx+b，当变换到k-b坐标系中，直线方程是b=-xk+y，其中斜率是-x，截距是y，由此可以看出k6坐标上的一条直线，可以表示为x-y坐标上经过特定点的一系列直线。在实际操作过程中，当斜率很大时直线坐标无法表示，故使用极坐标来表示：

ρ=xcosθ+vsinθ率为：

（3）

另外模拟退火算法在计算过程中以一定的概率引入一个扰动量，该扰动量的引入概率随时间的增加而降低。在热力学系统中，当前温度为T，存在能量差为Δt的概率是：

上面的式（4）是在每次迭代畸变校正系数的变化概率，把得到的改变的系数作为新的理想值，再进行验证和比较。畸变校正处理的流程如图3所示。

3 实验结果与分析

在变换过程中，精度和角度检测间隔的设置是比较重要的，为了能够有较好的结果，需要多次试验，找到合适的设置。另外在直线拟合过程中会导致线段的断裂，会影响计算的速度，在计算时舍去小于50个像素的直线。

2.3畸变校正系数的最优化

我们首先给定一个初始的系数，让系数在一定范围内变化，使得最优的结果能够快速地收敛经过若干次迭代后输出最优解，本文采用模拟退火算法[8]作为每次迭代的原理依据。

该算法将目标函数作为热量函数，当热量函数趋于稳定时，就可以认为得到了当前最优解。用数学语言描述为：设热力学系统s中有有限个且离散的n个状态，状态；的能量为Ei，在温度E「下，经过一段时间达到热平衡，这时处于状态i的概

我们利用霍夫变换进行直线检测，首先需要进行边缘检测以得到图片的边缘信息。为了减小霍夫变换的时间，我们对霍夫变换的不同参数进行设置，其中极值检测的检测间隔设置为2，即具有两个像素的间隔偏差，角度检测范围设置为-20：0.5：20，间隔是0.5，这样能够快速地实现检测，我们的回形图（见图4）只进行了竖列直线的检测，因为竖向方向的检测最优就可以表示为整体最优，并且能够使每一次进行模拟退火算法的迭代时间减小，加快计算速度。适应度的变化曲线如图5所示。

根据仿真结果可以看到，在30次迭代后最长直线的长度一直不变，保持在449，此时输出参数得到Ki=9E-10，K2=9E-10，P1=1E-8，P2=4E-8。由图4可知，最优结果已经能够检测到该回字形的最长边长，大约450个像素满足所求取得最优参数。

4 结语

本文根据光学镜头产生的畸变作出了的分析和研究，利用模拟退火算法进行迭代寻找最优的径向和切向畸变校正参数，其中我们根据物理平面的像平面的直线线性不变性，通过霍夫变换来检测矫正后圖像直线的最大长度，利用直线长度作为模拟退火算法的能量函数，每次迭代选择最优的作为当前输出解，多次迭代后趋于稳定，输出的结果即使最优的畸变校正参数设置。该方法的精度与霍夫变换的精确度有关，由于霍夫变换的精度设置在2 pixels，该方法在进行直线检测过程中会忽略大约2 pixels的范围。最后通过实际的畸变校正图像结果验证了该直线检测几何校正方法的准确性。