采用数据包络分析法的电力系统无功功率经济优化问题研究
吴 亮,马绍明,程鹏飞,张 鹏,范传忠
(1. 国网铁岭供电公司,辽宁 铁岭 112000;2.国网抚顺供电公司,辽宁 抚顺 113000)
由于无功功率不适合远距离大规模传输,因此系统中无功功率的补偿是通过就地补偿方式进行的,以此达到保持系统电压稳定、降低有功功率损耗、减少设备无功补偿费用的目的[1-4]。在以往无功优化问题研究中大部分是以有功功率损耗或电压质量为优化目标,本文从机组运行无功传输经济效率的角度出发,结合电网有功功率损耗作为优化目标函数之一,对电网无功功率进行优化计算。
数据包络分析法[5-7](data envelopment analysis)是在相对效率基础上发展起来的一种系统分析方法,它能够快速准确评价被判客体的有效性及相对有效性,本文使用粒子群算法结合数据包络分析方法对机组运行无功传输经济效率进行分析,在满足电网运行的条件下,达到全体机组运行无功传输经济效率及网络有功网损双重最优化。
1 无功功率优化模型
无功功率过量传输会造成电网有功损耗的增加,因此无功功率优化可以减少系统有功功率损耗,本文提出以系统无功功率传输为变量,优化无功分布以达到电网有功功率损耗最小的优化模型见式(1):
(1)
式中:K为电网中变压器支路的集合;ΔPi为第i台变压器支路上的有功功率损耗;G为电网中输电线路的集合;ΔPj为第j条输电线路上的有功功率损耗。
变压器支路有功损耗为
(2)
输电线路有功损耗为
(3)
式中:PiK为第i台变压器铜损;Pi为第i台变压器支路中传输的有功功率;Qi为第i台变压器支路中传输的无功功率;SiN为第i台变压器的额定容量;Pj为第j条线路中传输的有功功率;Qj为第j条线路中传输的无功功率;Vj为第j条线路额定电压;Rj为第j条线路电阻。
等式约束为
(4)
(5)
式中:PGi和QGi、PDi和QDi、Vi为节点i注入功率有功和无功功率、有功和无功负荷、电压幅值;Gij和Bij分别为节点i和节点j的互电导和互电纳;Vj为支路j的电压幅值;θij为节点i和节点j之间的相角差。
不等式约束为
PGmin≤PG≤PGmax
(6)
QGmin≤QG≤QGmax
(7)
QWmin≤Qk≤QWmax
(8)
VGmin≤VG≤VGmax
(9)
VLmin≤VL≤VLmax
(10)
SMmin≤SM≤SMmax
(11)
式中:PGmax、PGmin分别为发电机有功功率输出的上下限约束值;QGmax、QGmin分别为发电机无功输出的上下限约束值;QWmax、QWmin分别为无功补偿装置的上下限约束值;VGmax、VGmin分别为发电机电压上下限;VLmax、VLmin分别为节点电压上下限;SMmax、SMmin分别为线路传输功率上下限。
2 数据包络分析法模型
在美国著名的运筹学家A.Charnes和W.W.Cooper创立数据包络分析理论(DEA)以来,因为其具有所需要的指标少、不需要预先估算参数,而评价结果的灵敏性和可靠性高的特点被广泛应用来评价对象运行的有效性和效率[8-9]。
在数据包络分析理论中,被评价对象的特性是由决策单元决定的,每个决策单元都包含有相应的输入量和输出量。各个决策单元通过对输入量和输出量进行处理来实现对应的决策目标。
C2R模型是数据包络分析理论中最主要也是目前应用最广泛的模型,其主要内容如下。
设有n个决策单元,其中,第j个决策单元(xj,yj)的输入量和输出量分别为
xj=(xj1,xj2,…,xjk,…,xjn)
(12)
yj=(yj1,yj2,…,yjk,…,yjn)
(13)
对于第j0个决策单元,其输入量、输出量组成的单元设为(xj0,yj0)。
要对某个决策单元进行评价,就必须把各个输入量和输出量综合成一个可以作为评价指标的数。
(14)
式(14)为决策单元评价指标表达式,其中:u=(u1,u2,…,un)为输出量yj的权重系数;v=(v1,v2,…,vn)为输入量xj的权重系数;Vp为评价指标。从式中可以看出,Vp≤1。Vp越接近1,输入量xj对于输出量yj来说就越有效,即xj被充分利用的程度就越高。当Vp等于1时,则输入量xj与输出量yj是最佳匹配关系,即达到系统评价的最优状态。在被研究系统的历史数据已知的情况下,(xj,yj)为已知量,u和v是未知量,因此提高Vp的办法在于尽可能的改变u和v的值。所以构造C2R模型的目的在于量化u和v,使得Vp尽可能的接近1。经典C2R模型的表达式为
(15)
当引入新变量s+≥0.s-≥0时,则式(15)转化为
(16)
式(16)为引入松弛变量s+、s-时的C2R对偶模型,是C2R模型广泛使用的形式。式中,θ为当前被评价单元(x0,y0)的评价指标,反映其生产有效性。当θ越接近1时,评价单元(x0,y0)就越DEA有效。λj为输入量和输出量的权重,可以通过改变不同的权重值使得θ接近或者达到1。s+、s-为松弛变量,分别表示输出的不足量和输入的多余量。只有当θ=1且s+、s-都为0时,被评价单元才是绝对DEA有效的;否则仅当θ=1但s+、s-不都为0时,被评价单元为相对DEA有效,0<θ<1时,被评价单元为DEA无效,但随着DEA指标越接近1,被评价单位有效性越好。
在C2R对偶模型中,DEA有效指的是对应决策单元的综合有效性,综合有效性包含规模有效和技术有效。规模有效性指的是随着投入输入量的继续增多,则相应的输出量也在增多而不是减少;技术有效性指的是在投入同等的输入量,技术有效性高的可以获得更多的输出量或者是在同等产出的情况下,技术有效性高的可以投入更少的输入量。
3 基于粒子群算法和数据包络分析法(DEA)的无功功率多目标优化模型
3.1 粒子群算法
由于粒子群算法所需参数少,具有良好的寻找全局最优解的能力,也可有效避免算法早熟,因此本文采用粒子群算法求解电力系统无功优化问题[10-11]。
在粒子群算法中,假设解空间为n维空间。设xi=(xi,1,xi,2,xi,3,…,xi,n)为第i个粒子的位置,vi=(vi,1,vi,2,vi,3,…,vi,n)为第i个粒子的速度;pi=(pi,1,pi,2,pi,3,…,pi,n)为第i个粒子的历史最好位置。
vi,j(t+1)=wvi,j(t)+c1r1[pi,j-xi,j(t)]+c2r2[pg,j-xi,j(t)]
(17)
xi,j(t+1)=xi,j(t)+vi,j(t+1)
(18)
式中:w为惯性因子,决定着算法的搜索能力;c1、c2为学习因子,c1决定着粒子自身信息的传承,c2决定着粒子与整个群落信息的交换;r1和r2为[0,1]之间的满足均匀分布的随机数,决定着算法在全局搜索和局部搜索上的性能;xi,j(t)为第i个粒子的第j维在进行第t次迭代时在解空间所处的位置;pi,j为第i个粒子的第j维在以往迭代过程中产生的最好位置;pg,j为整个群落在第j维上的最好位置;xi,j(t+1)为第i个粒子的第j维在进行第t+1次迭代时在解空间所处的位置;vi,j(t+1)为第i个粒子的第j维在t+1次迭代时的移动速度矢量。
3.2 基于粒子群算法和数据包络分析法(DEA)的无功功率多目标优化计算模型
本文以式(1)作为目标函数之一;将系统内各机组作为数据包络分析的决策单元,同时以机组无功出力作为决策单元的输入量,以经潮流计算所得各节点电压与标准电压之间偏移量作为输出量,以式(14)做为另1个目标函数搭建无功功率多目标优化模型,约束条件为式(4)—(11)及式(16)所示。
4 实例计算分析
本文以IEEE14节点系统为例进行计算,算法参数设置:初始种群设为20;w=0.6:学习因子c1=0.75,c2=1.0,最大迭代次为1 500次,计算结果见表1、表2。

表1 IEEE14节点系统初始潮流结果
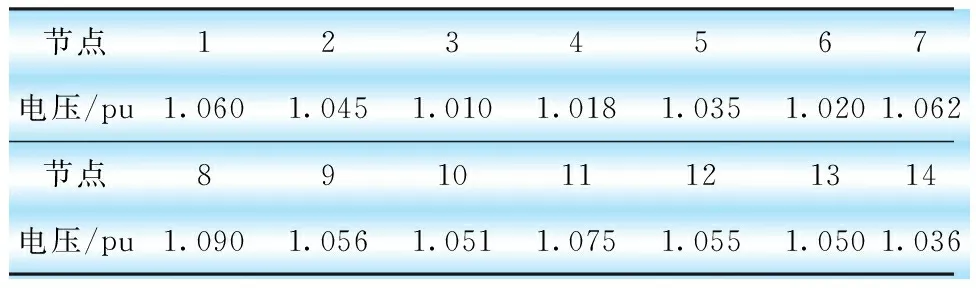
表2 IEEE14节点系统初始各节点电压计算结果
经过粒子群算法和数据包络分析法的无功功率多目标优化计算,计算结果见表3、表4。
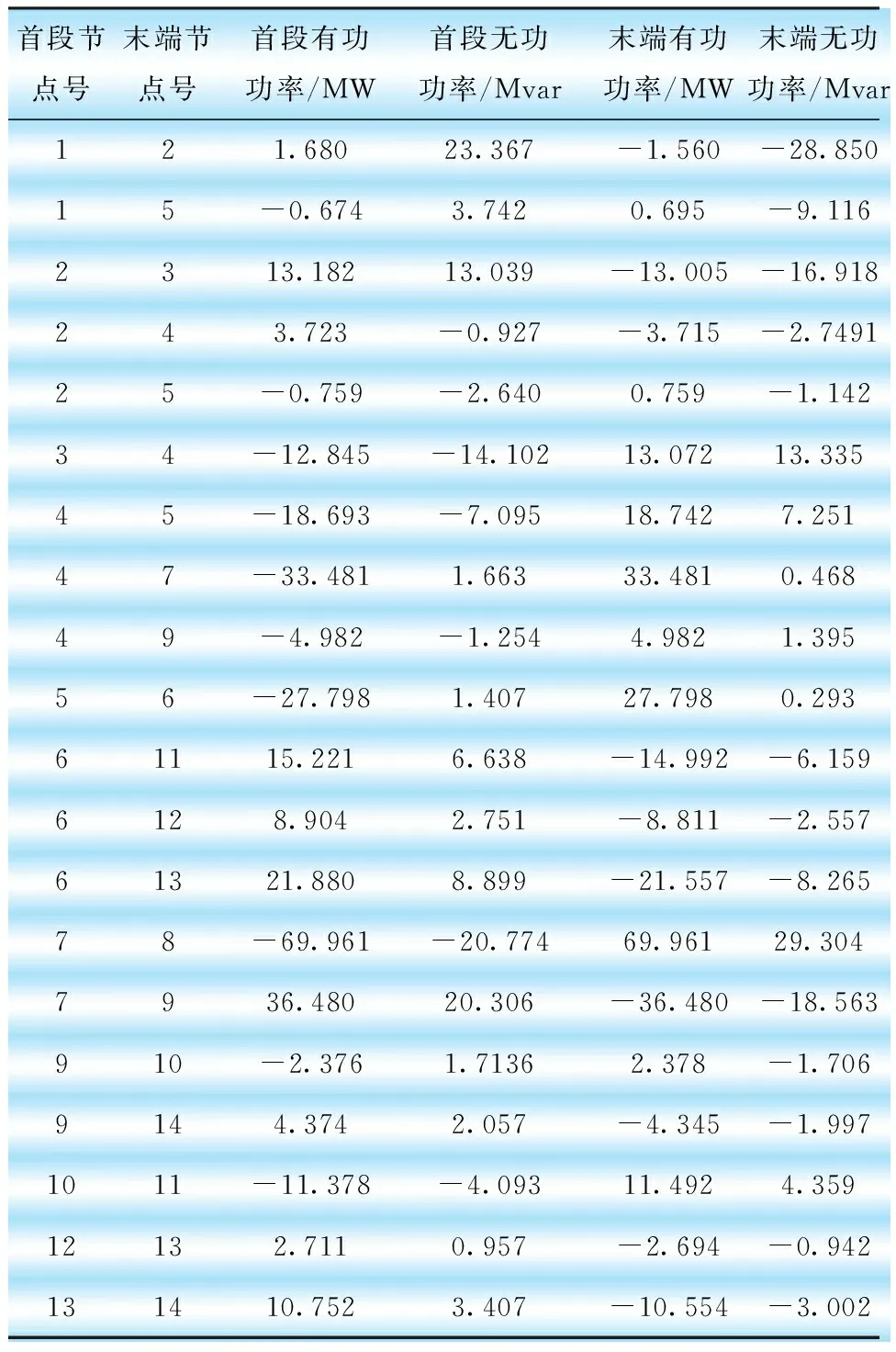
表3 IEEE14节点系统潮流优化结果
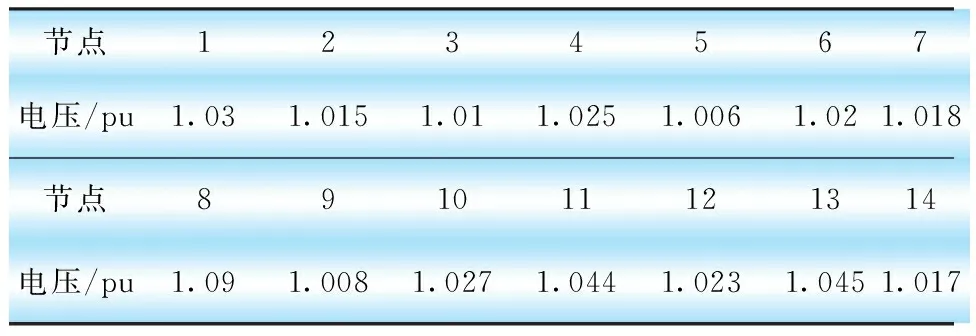
表4 IEEE14节点系统各节点电压优化计算结果
IEEE14节点系统原始潮流无功损耗约为54.54 Mvar,经过优化后系统无功损耗约为17.79 Mvar,经对比可知,无功损耗减少36.75 Mvar,网络中无功损耗情况得到很大的改观。原始数据IEEE14系统有功损耗约为13.393 MW,经过优化后有功系统损耗约为1.482 MW,经过对比,有功损耗减少11.911 MW,有功损耗也相应降低。
由表5和表6可知,表5中机组2、表6中机组3和机组4的DEA有效值θ均达到1,表明其机组运行经济效率最高,其余机组的DEA有效性指标θ均不为1,DEA有效值低于1表明经济效率有待提高。机组DEA有效值越接近1,其机组运行的经济效率越高,对系统而言机组的运行潜力开发越高。通过本文数据包络分析进行计算后可得知,在已经经过优化的电网中,机组3和机组4的经济运行效率得到充分开发,电力公司调整发电曲线时可从机组3和机组4着手,从而最大限度提高电网运行经济效率。
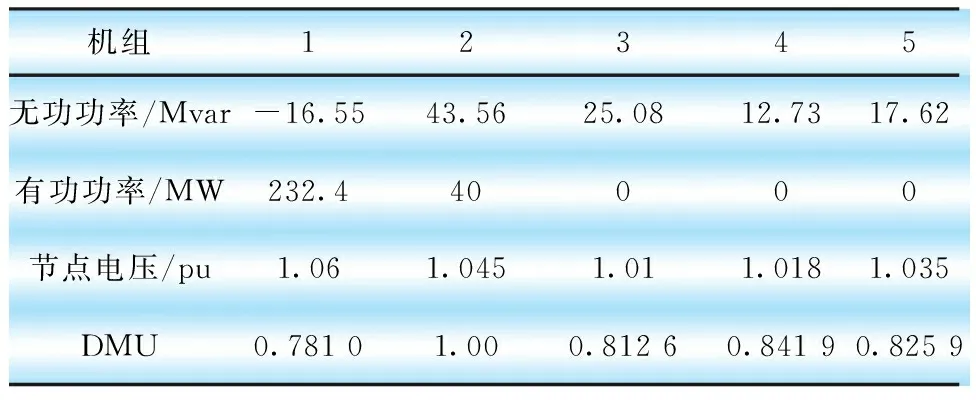
表5 初始机组数据包络分析指标

表6 优化后机组数据包络分析指标
5 结束语
针对传统的解决无功功率优化问题时集中关注于系统有功损耗最小的情况,本文通过采用粒子群算法和数据包络分析方法对系统无功功率进行优化,从提高机组运行无功经济效率的角度出发,将提高机组运行无功传输经济效率与降低有功损耗并重,通过算例证明本文所提方法在降低系统有功损耗和提高机组运行无功传输经济效率方面具有双重指导意义。
参考文献:
[1] 郝思鹏,王正风.电力市场下的无功定价研究[J].继电器,2006,34(19):51-54.
[2] 代红才,彭建春,杨帮宇,等.基于边际成本和潮流追踪的无功定价[J].电网技术,2007,31(7):59-63.
[3] 张勇军,任 震,李邦峰.电力系统无功优化调度研究综述[J].电网技术,2005,29(2):50-56.
[4] 岳 青,魏宇存,孙 蕾,等.榆林电网无功优化运行研究[J].电工电气,2012, 3(3):21-25.
[5] 魏权龄.数据包络分析(DEA)[J].科学通报,2000,45 (17):1 793-1 808.
[6] 罗道平,肖 笛.数据包络分析(DEA)在电力工业的应用[J].系统工程理论与实践,1996, 4(4):60-66,112.
[7] 楼旭明,窦彩兰,汪贵浦.基于DEA的中国电力改革绩效相对有效性评价[J].当代财经,2006,4(4):90-93.
[8] 解百臣,吴育华.基于SE-DEA的电力企业效率评估[J].电子科技大学学报(社科版),2005,7(4):25-27.
[9] 朱春波. DEA在电网企业投入产出绩效评价中的应用研究[D]. 重庆:重庆大学,2008.
[10] 曾嘉俊,刘志刚,何士玉,等.一种基于子区域粒子群的无功优化算法研究[J].电力系统保护与控制,2012,40 (1):37-42.
[11] 侯云鹤,鲁丽娟,熊信艮,等.改进粒子群算法及其在电力系统经济负荷分配中的应用[J].中国电机工程学报,2004,24(7):99-104.

