内地多港口间的集装箱配载最优方案
郑斐峰,梅启煌+,王 璐,张小宁
(1.东华大学 旭日工商管理学院,上海 200051;2.上海民航职业技术学院 基础教学部,上海 200232;3.同济大学 经济与管理学院,上海 200092)
0 引 言
集装箱配载问题[1]的基本目标是保证船舶在运输过程中的船体平衡安全。对应地,装卸操作需要遵从两条规则:①离港时船舶上的每个集装箱堆列满足重箱在下轻箱在上的码放规则;②所有堆列的箱子重量分布满足在船舶前后端、左右侧的平衡规则。通过设计满足上述装载规则的具体配载方案,提高船舶在港装卸效率以及运输效率。在装卸操作时,不妨把从码头堆场装载到船上以及从船舶卸载到堆场的集装箱称为目标箱,同时,将船上的其它集装箱均称为非目标箱,对非目标箱的每次临时卸载或者装载操作都称作一次翻箱。
近年来,不少的研究学者都对配载问题进行了研究,Delgado等[2]对于大型的集装箱船的装载成本进行研究,提出的模型能够在1 s内实现236个实例中的90%;Monaco等[3]以最小装载时间为优化目标建立优化模型,并设计出两阶段启发式算法,验证了模型的有效性;Kevin等[4]对港口内部集装箱运输情况进行研究,以最小化集装箱交付延迟时间为目标,建立两步式求解步骤模型,通过应用文中的模型能够解决现实中的很多实际情况,并且有利于解决交通拥堵和交付延迟惩罚等问题,对集装箱运输的长期决策具有一定的指导作用;Liu等[5]研究岸桥双循环和优化集装箱船内部的翻箱操作的问题,以总的服务时间和启动时间为目标,设计了一种在多项式时间内的启发式算法,并将此方法与目前最先进的方法进行比较,结果表明作者提出的方法更能有效的解决此问题的模型,并且该算法能够在数秒钟内对现实世界中的实例得出方案,极大提高了装载效率。
从以上文献可以看出,这些都是以单个港口为研究背景,没有考虑到整条航线过程中的多个港口的配载情况。Francisco等[6]对集装箱配载问题主要是对贝位的配载情况进行研究,与以往不同的是,文中提出明确处理已出货的集装箱和对危险箱的分离规则两个特点。对集装箱的配载问题建立整数规划模型,并设计出贪婪随机自适应搜索算法。仿真结果表明,该方法能够快速获得高质量的求解方法,并与以往研究中相同的实例进行比较分析,表明文中提出的算法对于求解此类问题可以取得更好的结果。Azevedo等[7]充分考虑航线中集装箱船舶的装载与卸载的不同操作,分析出12种不同的装载和卸载的过程。在此基础上依据遗传算法、模拟退火和光束搜索3种算法开发出启发式算法求解3D集装箱的装载问题。文中设计的编码方式能够始终保持所有的解都是可行解,极大缩短了运算时间。在一些实例中,可行解的值还能够非常接近下界值,表明文中的方法对于港口的实际操作有一定的指导意义。Araújo等[8]将集装箱看作是一个三维的结构,提出一个旨在维持稳定性及最小化翻箱数量的帕累托聚类搜索方法来解决3维集装箱的配载问题,并将元启发式算法和本地搜索启发式算法相结合,通过数值模拟实验证明该方法的效果比单目标的模拟退火算法更好。Ding等[9]通过设计一个启发式算法解决集装箱船在多港口航线中的总翻箱数量最小的问题,并将该启发式算法与Avriel提出的启发式算法相比较,结果表明文中的方法对于解决此类配载问题有着更好的效果。Ambrosino等[10]在已有的单港口配载模型的文献基础上,建立了一个多港口主贝位配载计划的混合整数规划模型,以船舶最小化在港时间为目标,利用混合整数规划设计启发式算法在短时间内求出集装箱的配载方案,从而帮助计划制定人员更好应对航行过程中变动的运输需求。实验结果表明,该方法能够高效得出装载多于18000TEUs的集装箱配载方案。
另外,Wei等[11]、Wang[12]、Carlo[13]、Zhang[14]和Ramos等[15]也对堆场配载和配载复杂性等问题做了相关的研究。在关于配载问题的相关文献中,大部分都是关于单个港口配载计划的文献,多个港口配载计划的文献相对较少,前人的研究大多是以船舶的在港时间或装载时间作为目标。文中不只是对单个港口的配载情况进行优化,主要针对多港口的集装箱船配载问题,以最小化的总航线的翻箱数量为目标,在考虑船舶稳定性的基础上,提出从考虑所有翻箱的可能性角度出发,充分考虑整个航线中的具体翻箱操作,建立0-1整数规划模型,使得整个航线过程中翻箱的数量达到最小,最后利用CPLEX对中小型集装箱船单个贝位的装载实例进行求解得出精确的配载方案,提高了港口的运作效率,弥补了以往研究在中型集装箱船配载问题中无法快速取得精确解的不足,对现实中我国如武汉港、芜湖港等内地港口船舶配载有实际的指导意义。
1 问题描述
集装箱船舶在码头进行装卸操作时,船上每一个贝位的所有目标箱的装卸工作只能由一个岸桥来完成,在此过程中涉及的非目标箱翻箱作业也必须在该贝位内由同一个岸桥进行操作。由于目标箱本身的装卸操作时间是确定的,因此,贝位内的装卸效率大小取决于非目标箱的翻箱次数或时间。要降低艘船舶的在港逗留时间或者提升装卸效率,其中一个可行的思路就是设法减少贝位内的翻箱次数。考虑船舶在整条航行路线中需要历经上下游多个港口,因此,为了提升它在整条航线上的运输效率,就要减少它在所有港口非目标箱的翻箱总次数。假定所有岸桥的作业效率相同,则每个贝位在任一港口的作业效率取决于该贝位内的翻箱作业量。本研究以船舶的某个贝位作为具体分析对象,研究该贝位在多个港口中的配载计划方案,以实现在船舶的整个运输过程中,该贝位的翻箱次数最少的优化目标。
图1是一个平面二维上的集装箱船舶示意图。从船舶的侧面看,船头至船尾接连堆放的集装箱组成了不同的贝位,一个贝位的宽度等于一个集装箱的长度;每个贝位从甲板的左侧至右侧码放着许多列的集装箱,每一列上垂直堆放着多个集装箱,一个箱子占用一层的位置。因此,每个集装箱在船舶上的位置可以用它所在的(列,层)编号来表示。这里,假设所有的集装箱都是20英尺的TEU标准箱。
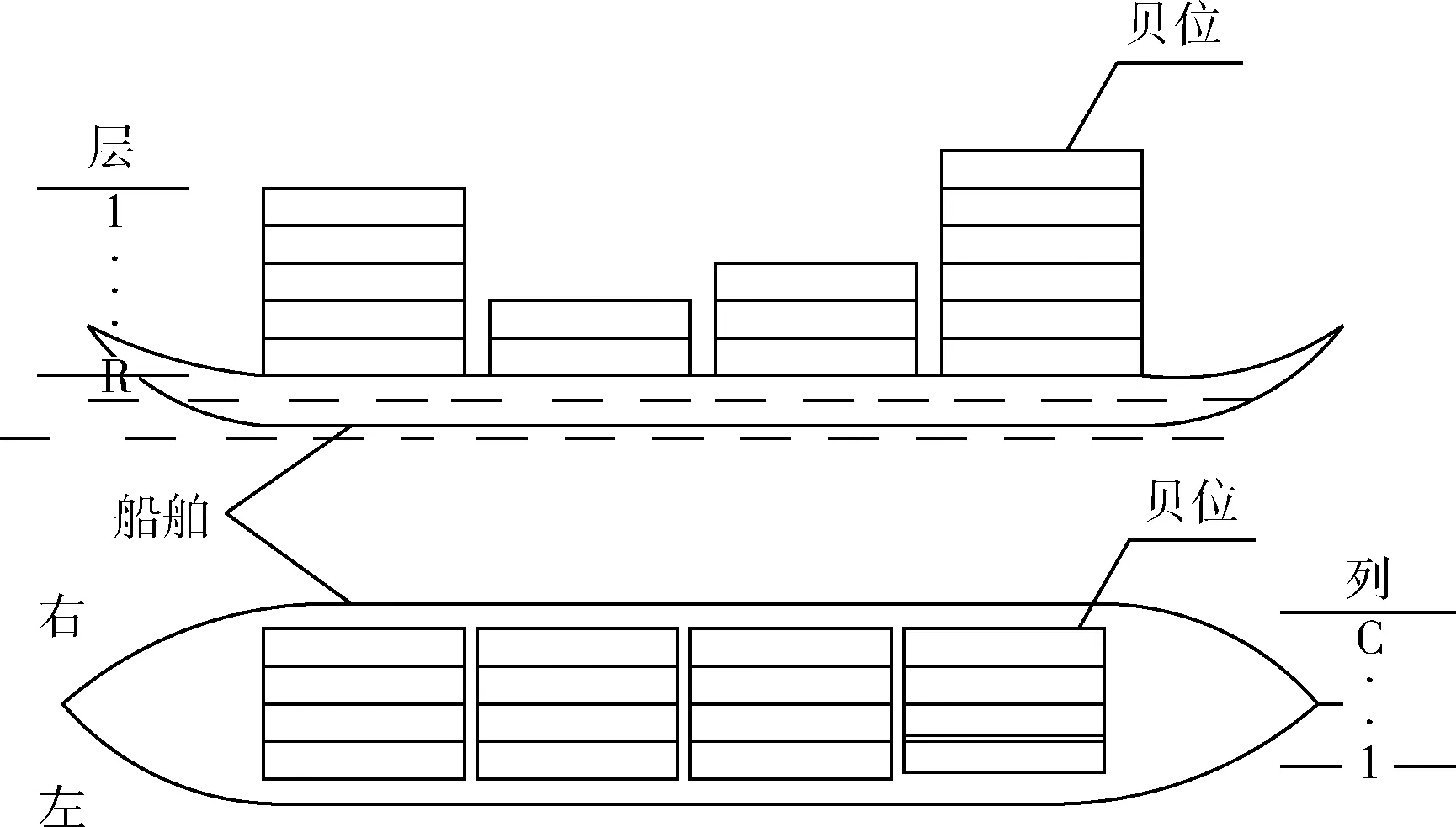
图1 集装箱船的侧视和俯视
考虑多港口的单贝位配载计划问题研究主要基于以下一些基本假设:
(1)船舶依次停靠1,2,…,T港口,在各个港口的所有目标箱信息事先已知。在港口1只有装载操作,而在港口T只有卸载操作并且船上所有集装箱都要求卸载;
(2)为了员工操作简单,非目标箱的翻箱不允许在甲板不同列之间直接进行操作,它必须包括临时卸载和再次装载两次操作,而且翻箱操作只在该贝位内进行;
(3)所有集装箱的重量分为1,2,3这3个等级,数字越大表示集装箱越重。在任一时刻船舶上的所有集装箱列必须满足重箱在下轻箱在上的码放规则;
(4)基于配载安全要求,每一列的集装箱数量以及集装箱总重量均有一个规定上限。
在相关文献中,理工学院Avriel等假设每个集装箱的翻箱成本都为1,以此来求的最小的翻箱成本,实质上与翻箱数量是相同的,翻箱成本即为最终的翻箱数量,而且文中的模型并没有考虑贝位中的重量约束,集装箱重量不同的情况以及航线中船舶的稳定性。梁承姬等[16]考虑了单港口集装箱船装载计划,在堆场中的预翻箱数量问题,孙等[17]假设集装箱在某港口产生翻箱时,先后两次的位置是不相同的,而在实际中,翻箱先后的两次位置也是有可能会是相同的,文中考虑的是所有翻箱的情况,包含翻箱先后两次位置相同和不相同的情况。
2 模型建立
2.1 符号说明
(1)索引
t:表示港口的序号;
i,j:表示集装箱的序号;
c:表示贝位中列数的序号,从左到右依次是1,2,3,…,C;
r:表示贝位中层数的序号,从上到下依次是1,2,3,…,R;
(2)参数
T:航线中港口的集合,t=1,2,3,…,T;
C:每个贝位中的总列数;
R:表示贝位中每列的总层数;
N:T个港口中装载的集装箱的集合,i,j=1,2,3,…,N;
wi:第i个集装箱的重量;
si:向船舶中装载的第i个集装箱的出发港口;
di:从船舶中卸载的第i个集装箱的目的港口;
Dt:在第t个港口目标箱的集合,即,Dt={i|di=t}∪{i|si=t};
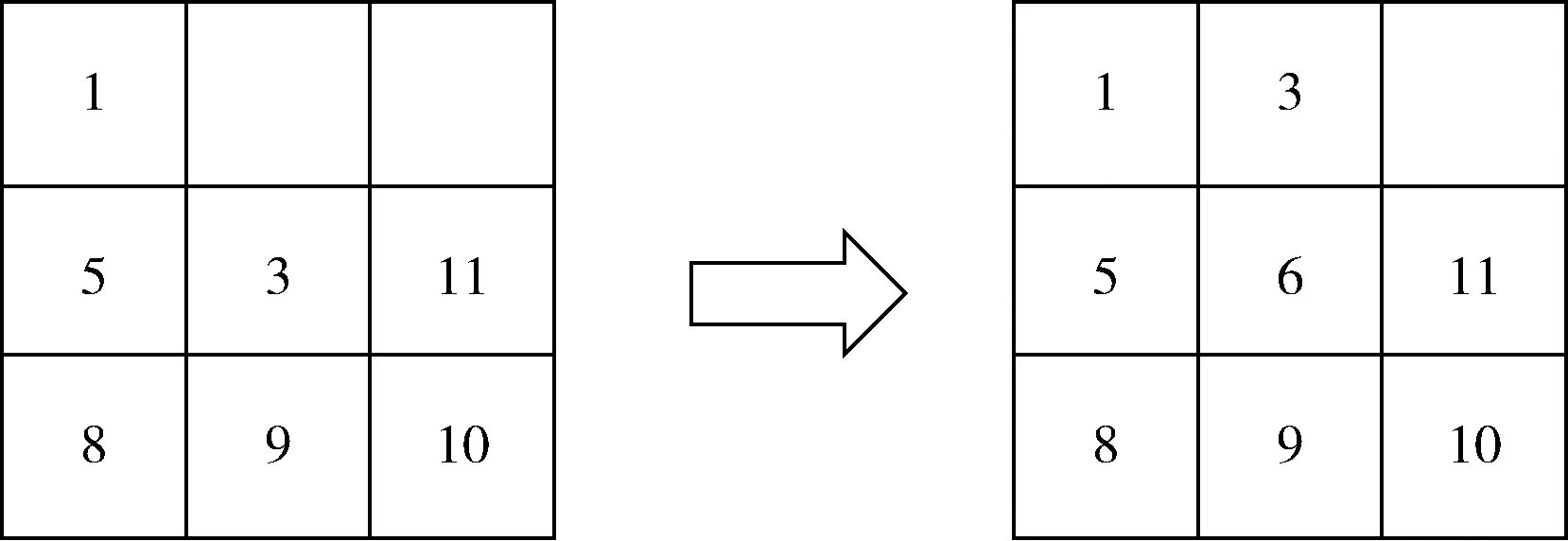
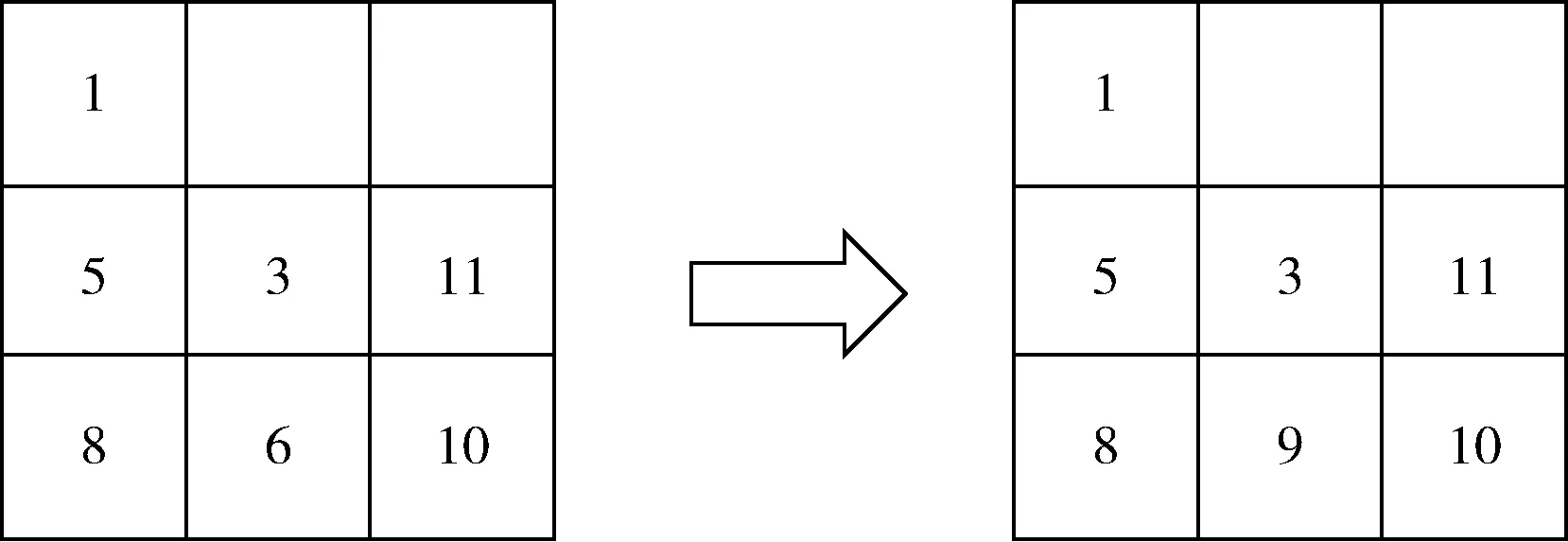
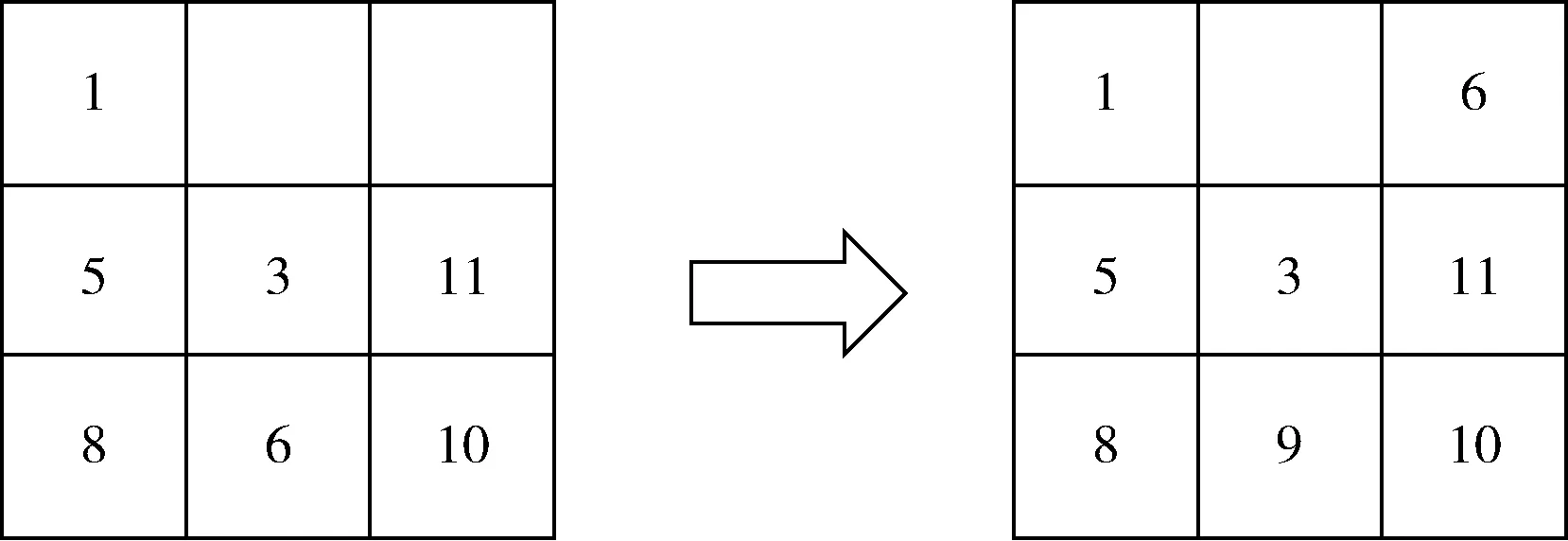
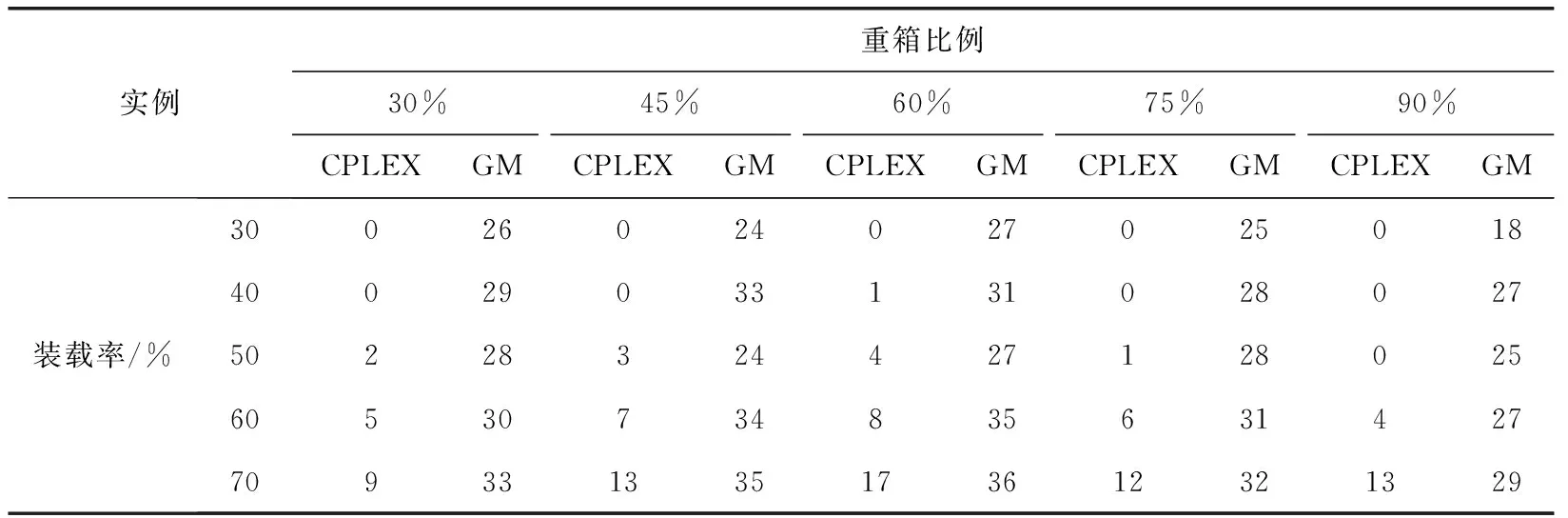
Ut:在第t个港口非目标箱的集合,即,Ut={i|si W:贝位中每一列允许的集装箱最大载重量; M:一个充分大的正整数; (3)决策变量 根据在整个航线过程中,保证船舶运输安全的情况下,最小翻箱的目标,建立如下的0-1整数规划模型 (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) i,j∈N,r,c∈Z+,r≤R,c≤C,t∈T (16) 目标函数(1)表示最小化整条航线中的翻箱数量;约束(2)和约束(3)指任意一个集装箱i的出发港口si大于目前所停靠的港口t或者目的港口di小于目前所停靠的港口t,这两种情况下,集装箱i都不能被装载在贝位的任何一个箱位上;约束(4)表示在航线中的任何港口,任何一列上所有集装箱的总重量不能超过规定的总重量W;约束(5)表示在航线中的任何港口,任何一列上所有的集装箱的总数量不能超过总的层数R;约束(6)表示在航线中的任何港口,任何一个箱位上最多只能装载一个集装箱;约束(7)任意一个已经被装载到贝位上的集装箱在还没有到达目的港口之前,一定是在贝位中的一个箱位上,不能被提前卸载;约束(8)在航线中的任何一个港口的任意一列上,如果一个箱位上已经被装载了集装箱,那么它的下一层也一定装载了集装箱;约束(9)表示在航线中的任何港口,任何一列上都必须满足重量大的集装箱必须装载在重量小的集装箱的下面;约束(10)船舶离开航线中的任意一个港口(除了最后一个港口)时,贝位中集装箱的位置与刚到达下一个港口时位置是相同的;约束(11)在集装箱船到达最后一个港口时,所有的集装箱都应该被卸载;约束(12)如果非目标箱i在进入港口t与离开港口t时的位置不同,那么它一定会产生一次翻箱,如图2和图3所示;约束(13)在船舶到达港口t时,集装箱i是装载在(c,r)箱位上的非目标箱,如果在集装箱i同一列的下面存在一个目标箱j,即使集装箱i的位置没有发生变化,它在t港口也一定会产生一次翻箱,如图4所示,集装箱6被卸载,集装箱9被装载到了原来集装箱6的位置上,虽然集装箱3 的位置没有变化,但是集装箱3一定产生过一次翻箱操作;约束(14)在船舶到达港口t时,集装箱i,j是装载在同一列上的两个非目标箱,并且集装箱i装载在j的下面,如果集装箱i在港口t被翻箱一次,那么即使集装箱j的装载位置在离开港口t时没有产生变化,集装箱j在港口t也一定产生了一次翻箱,如图5所示,集装箱6被装载到了其它的位置上,集装箱9装载到了原来集装箱6的位置上,虽然集装箱3没有改变位置,但是集装箱3肯定产生过一次翻箱操作;约束(15)和约束(16)分别表示决策变量和各参数的范围。 图2 目标箱6在第2列中被卸载 图3 目标箱6被装载到第2列中 图4 装载和卸载的集装箱在同一个箱位上 图5 非目标箱6在进港和出港时改变了位置 贪婪算法是指,在对问题求解时,不从整体最优上加以考虑,所做出的是在某种意义上的局部最优解,有时甚至可以达到全部最优解。在实际的集装箱运输过程中,港口的工作人员一般都是根据以往的工作经验进行船舶集装箱的配载工作,文中针对这一配载情况,采用贪婪策略进行研究如下: 步骤1 将每个港口所装载的集装箱按照重量大小排序,重量相同的按照目的港口由近到远排列; 步骤2 将重量相同的集装箱装载在贝位同一列中,目的港口较远的优先装载; 步骤3 在每列中满足重箱在下轻箱在上的装载规则,并且每列装载的数量不能超过规定值,满足层数约束; 步骤4 检验每列的装载重量和层数,若不满足重量限制,则将最上面的集装箱与目的港口相同且较轻的集装箱交换装载位置或者将该集装箱装载到新的一列上,直到满足每列的重量约束; 步骤5 根据翻箱规则,计算多港口间的总翻箱次数。 从运力上来看,大型集装箱船(5000TEUs以上)的运力与小型集装箱船(3000TEUs以下)达到了相同的比例,加上中型集装箱船,则中小型船达到了63.3%的比例,中小型集装箱船仍然占据着主要的地位。文中的模型针对我国内地港口的发展情况,对中小型集装箱船的配载问题能够很快得以解决,并且能够直接求得最优的配载方案。以下是文中精确解与文献中精确解的比较分析,见表1。由表1中结果分析可知,文章中的方案可以求解出多个港口较大运输量的集装箱配载方案。 表1 文章精确解与文献精确解的比较 为了考虑船舶航行的安全性,结合实际情况考虑,甲板上装载的集装箱最高只能达到8层。假设集装箱的重量有3种等级,分别为1、2、3,重量为1代表轻箱,重量为2代表中型箱,重量为3代表重箱;船舶上每个贝位一共装载7列,并且贝位中的每一列上的重量不超过23,重量越大的集装箱装载的层数越低。船舶从第一个港口开始,分别经过2、3、4、5、6、7港口,最终到达第8号港口,并且在第一个港口时船上不存在集装箱,只进行装箱操作,当船舶到达最后一个港口时,集装箱应全部被卸载。在多港口的实际配载过程中,由于每次装载集装箱的重箱比例以及航线中船舶的装载率并不一定都是保持不变,因此文章针对航线中集装箱船的装载率以及集装箱不同等级的重量比例进行仿真实验。分别对30%、40%、50%、60%、70%的装载率下重箱比例分别为30%、45%、60%、75%、90%的配载情况,利用模型和贪婪策略进行实验分析,仿真实验的结果见表2。 表2 不同装载率以及不同重箱比例下的翻箱结果 注:GM表示贪婪算法。 随着装载率和重箱比例的不断增加,贪婪算法对于求解此类问题也逐渐产生较好的方案。通过查阅相关资料所得,在内地港口翻箱一次所产生的费用大约是100元,每次的翻箱时间为3分钟。当船舶航线中装载率为30%时,文章中的算法比贪婪算法所提出的配载方案能使班轮公司每次航行平均大约节约2400元,节省72分钟;而当装载率为70%时,每次航行大约能节约2000元,节省60分钟。 近年来,长江流域是我国最具经济活力的地区之一,增速达到年均10%。由于长江沿岸集装箱运输发展迅速,虽然出现了“一哄而起,赶潮进入”现象,使得竞争加剧,但是仍然有大量的资金融入市场,对于船运公司和港口码头来说,这是一个新的机遇与挑战。根据相关文献统计,长江沿岸集装箱货物装载率大约为50%至70%左右,而重箱的比例大约是50%至60%左右[19]。进一步说明文中的研究与长江沿岸集装箱船舶的实际装载情况相符合。 由以上分析可知,虽然随着装载率和重箱比例的逐渐增加,贪婪算法求解的配载方案也逐渐优化,但文中模型中的方法比贪婪算法更有效。同时与贪婪算法相比,也进一步降低了班轮公司的运输成本并且提高了港口的工作效率,对我国长江沿岸港口集装箱的配载情况具有一定的指导作用。 配载计划一直是集装箱运输的一大环节,制定出合理的配载方案是提高集装箱装载效率的关键。针对以往研究中大多是以在港时间和装载时间为目标的配载研究,在维持航行过程中船舶稳定性的情况下,建立了0-1整数规划模型,提出考虑航线中所有港口的各种可能产生翻箱的情况,详细的记录了每个港口集装箱的位置,具体的描述了每个港口的翻箱操作,以最小化航线过程中翻箱的数量为目标,解决了每个贝位在整条航线中精确配载问题,对于我国内地港口的中小型集装箱船的配载研究具有一定的指导意义。 另外,针对多港口集装箱配载问题,由于船舶的稳定性受诸多因素的影响,航行过程中整个船舶的配载情况,船首和船尾装载的重量差以及船舶左右装载的重量差限制,重心的倾斜程度等。考虑影响船舶配载的各种因素,提高装载的效率,降低运营成本,这是下一步研究的重点。 参考文献: [1]Surging News.A ship roll 44 containers down the river,all the salons overnight salvage in Shanghai[EB/OL].[2016-05-02].http://www.thepaper.cn/newsDetail_forward_1463772(in Chinese).[澎湃新闻网.上海一轮船侧倾44只集装箱落江,经一夜打捞全部出水[EB/OL].[2016-05-02].http://www.thepaper.cn/newsDetail_forward_1463772.] [2]Delgado A,Jensen R M,Janstrup K,et al.A constraint programming model for fast optimal stowage of container vessel bays[J].European Journal of Operational Research,2012,220(1):251-261. [3]Monaco M F,Sammarra M,Sorrentino G.The terminal-oriented ship stowage planning problem[J].European Journal of Operational Research,2014,239(1):256-265. [4]Tierney K,Voß S,Stahlbock R.A mathematical model of inter-terminal transportation[J].European Journal of Operational Research,2014,235(2):448-460. [5]Liu M,Chu F,Zhang Z,et al.A polynomial-time heuristic for the quay crane double-cycling problem with internal-reshuffling operations[J].Transportation Research Part E,2015,81:52-74. [7]Azevedo A T D,Ribeiro C M,Sena G J D,et al.Solving the 3D container ship loading planning problem by representation by rules and meta-heuristics[J].International Journal of Data Analysis Techniques & Strategies,2014,6(3):228-260. [8]Araújo E J,Chaves A A,Neto L L D S,et al.Pareto clustering search applied for 3d container ship loading plan problem[J].Expert Systems with Applications,2015,44(1):50-57. [9]Ding D,Chou M C.Stowage planning for container ships:A heuristic algorithm to reduce the number of shifts[J].European Journal of Operational Research,2015,246(1):242-249. [10]Ambrosino D,Paolucci M,Sciomachen A.A MIP heuristic for multi-port stowage planning[J].Transportation Research Procedia,2015,10:725-734. [11]Wei L,Zhu W,Lim A.A goal-driven prototype column ge-neration strategy for the multiple container loading cost minimization problem[J].European Journal of Operational Research,2015,241(1):39-49. [12]Wang S.Optimal sequence of container ships in a string[J].European Journal of Operational Research,2015,246(3):850-857. [13]Carlo H J,Vis I F A,Roodbergen K J.Transport operations in container terminals:Literature overview,trends,research directions and classification scheme[J].European Journal of Operational Research,2014,236(1):1-13. [14]Zhang Z,Lee C Y.Multiobjective approaches for the ship stowage planning problem considering ship stability and container rehandles[J].IEEE Transactions on Systems Man & Cybernetics Systems,2016,46(10):1374-1389. [15]Ramos A G.Dynamic stability metrics for the container loa-ding problem[J].Transportation Research Part C,2015,60:480-497. [16]LIANG Chengji,ZHENG Juanjuan,LIU Yang.Container pre-marshalling simulation research based on heuristic algorithm[J].Computer Simulation,2014,31(12):416-420(in Chinese).[梁承姬,郑娟娟,刘扬.基于启发式算法的集装箱预翻箱问题仿真研究[J].计算机仿真,2014,31(12):416-420.] [17]SUN Junqing,CHEN Chen,LIU Fenglian.On stowage planning for mult-port container transportation based on stabi-lity constraint[J].Computer Engineering and Applications,2012,48(32):236-243(in Chinese).[孙俊清,陈忱,刘凤连.考虑船舶稳定性的多港口集装箱配载问题[J].计算机工程与应用,2012,48(32):236-243.] [18]Cruz-Reyes L,P H H,Melin P,et al.Constructive algorithm for a benchmark in ship stowage planning[M].Recent Advances on Hybrid Intelligent Systems. Springer Berlin Heidelberg,2013:393-408. [19]HAN Jingwei.Research on the development of the yangtze river container logistics space[J].Research on Economics and Management,2014(3):103-109(in Chinese).[韩京伟.长江内河集装箱物流发展空间研究[J].经济与管理研究,2014(3):103-109.]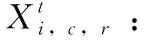
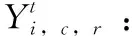
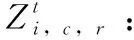
2.2 建立0-1整数规划模型
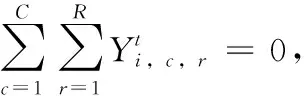
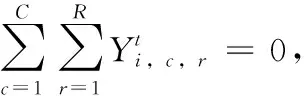
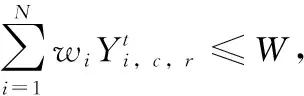
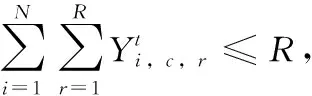
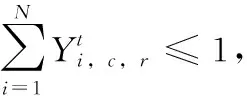
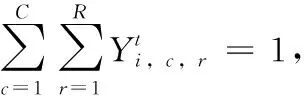
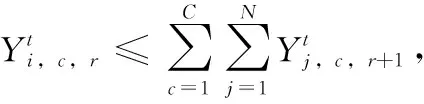
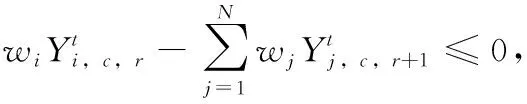
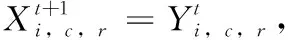
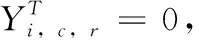
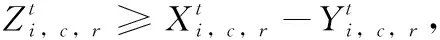

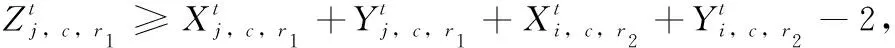

3 贪婪算法及实例分析
3.1 贪婪算法
3.2 实例分析

4 结束语

