电液伺服系统的故障自愈设计与仿真
孙文理,袁宇浩,袁 野
(南京工业大学 电气工程与控制科学学院,江苏 南京 211816)
0 引 言
电液伺服系统由电信号处理元件和液压动力结构构成,是一个兼具液压和电气两方面技术优势的反馈控制系统。因其控制准度高、反应速率快等优势,被广泛应用于航天航空、船舶作业系统以及钢铁制造装备等科学技术领域[1]。
随着现代工业的发展,大型机电系统是否能够安全可靠地以最佳状态运行,对于提高企业生产能力,确保生产安全具有十分重要的意义。如果系统的某个单元发生了故障,很容易产生连锁反应,引起系统的其它部位也发生不同程度的故障,这些故障不仅会造成严重的经济损失,甚至还会危及人的生命安全[2-4]。为了从根本上解决系统的故障诊断和修复,研究人员不断地对常规方法进行改进,并提出新思路。故障智能自愈思想就是在这样的大环境下应运而生[5-7]。
1 电液伺服系统的建模及故障分析
1.1 电液伺服系统的组成及工作原理
电液伺服系统主要包括以下基本元件:指令元件、检测元件、比较元件、液压控制元件、执行元件、控制对象以及液压能源装置等[8],如图1所示。
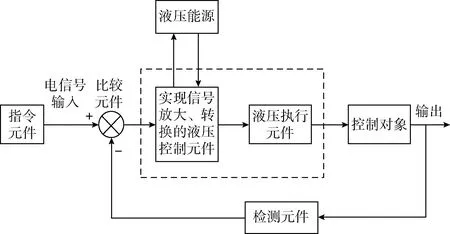
图1 电液伺服控制系统
系统的工作原理可简述为:指令元件发出的电信号作为输入,与检测元件反馈的电信号进行比较。将给出的误差信号进行放大、转换成液压信号传给执行元件。执行元件负责实现调节动作,满足控制对象的调节要求[9]。
1.2 基于HCD库的电液伺服系统建模
在AMESim(advanced modeling environment of simulation)中,预先提供了众多的数学模型。将这些数学模型进行归类,使其成为仿真模型“库”。AMESim软件中还包含了一个HCD库,如果在软件自带的模块中找不到需要的模型,可以利用HCD库搭建出需要的各种模型。HCD库的理念是能够让使用者以最少的子模型数,去构建最多的液压元部件模型[10]。
液压缸的HCD模型如图2所示。子模型BAP11和BAP12代表了活塞两侧的腔体。左右两侧的压力分别由所属子模型处理,压力作用的方向由BAP11和BAP12内箭头所示。子模型BHC11是与两个“半活塞”相连的液压腔(ch),用于模拟压力的动态性。压力的动态特性只与缸体内部的流体体积有关,该体积随活塞位置的不同而改变。将基于HCD库设计的液压缸模型用于电液伺服系统的模型搭建,如图3所示。
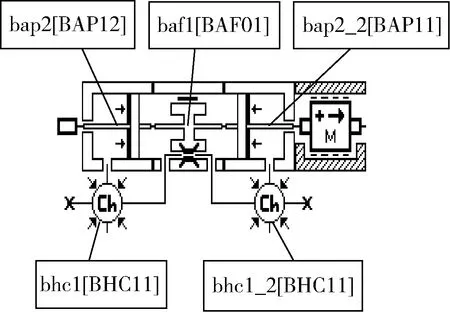
图2 液压缸的HCD模型

图3 基于HCD库设计的电液伺服系统
比较原液压缸标准子模型与HCD优化后的子模型仿真图像,验证了HCD构建模型的准确性,且发现经过HCD库优化设计的模型,在系统响应速度上更快、更稳定,并且波动更小,如图4所示。
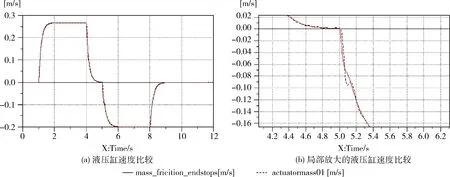
图4 液压缸活塞速度比较
1.3 电液伺服系统故障仿真及分析
电液伺服系统故障大多是由系统元件的重要特性或运行参数的变化引起的,也有可能是系统硬件部分损坏导致的。当系统发生故障时,系统的运行状态会受到影响,也可能导致系统无法完成正常的功能[11,12]。本文主要针对放大器故障进行仿真分析,为电液伺服系统的故障自愈奠定基础。
放大器中的放大器增益kp是引起电液伺服系统放大器故障的主要因素。标准运行中,系统放大器的增益kp设为300。利用故障注入的方法,将不同的kp值赋值给系统,研究分析其故障现象。液压缸活塞速度图像如图5所示。由图5(a)、(b)比较可以看出,当kp为100小于标准值时,液压缸活塞速度达到最快速度时间更长,其响应速度较慢。但当kp为500后,液压缸活塞速度开始出现明显震荡波动,且随着kp增大,其震荡波动程度加剧。
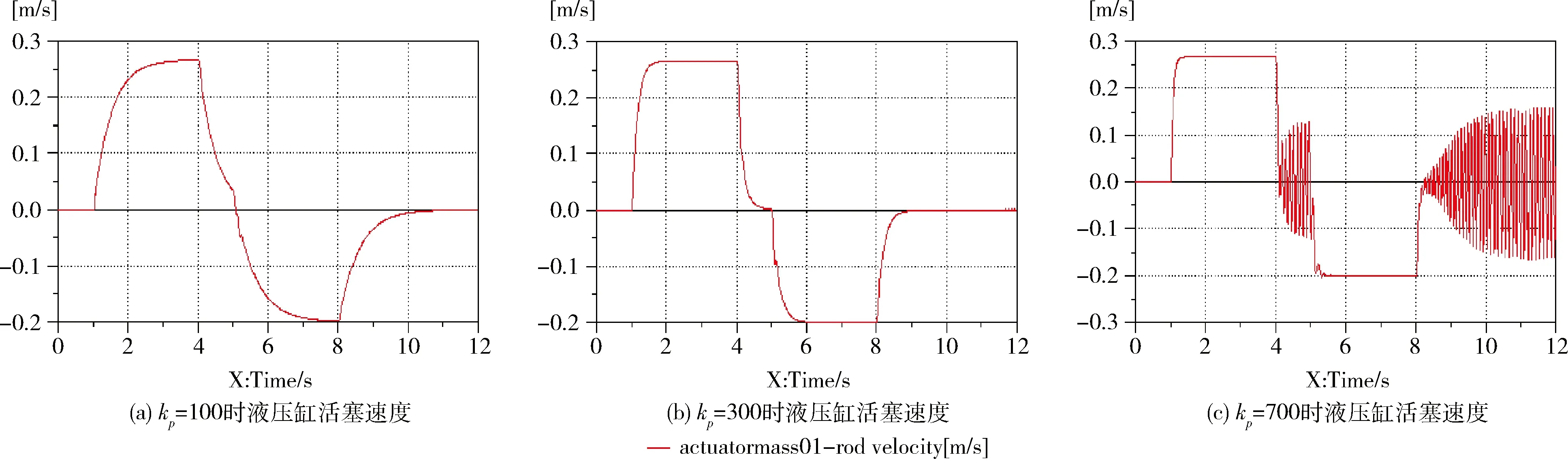
图5 液压缸活塞速度
2 电液伺服系统故障自愈设计
2.1 基于人工免疫的自愈原理
自然界的生物免疫系统所拥有的多层保护、自诊断、自匹配策略等免疫机制为故障自愈系统的设计提供了思路和方法。免疫系统能识别抗原并对抗原进行免疫应答,这种识别不需要精确匹配,是通过免疫系统中抗原与抗体的识别机制来完成的[13]。系统在进行自愈调控时通常包括3个阶段:正常运行阶段、故障产生阶段和故障后阶段。这3个阶段都是在无人干预的情况下系统自己维持稳定有序的运行。
结合系统故障自愈调控的3个阶段,从完成系统既定功能角度,把故障自愈系统结构分作自愈决策层、自愈执行层和免疫自愈层。自愈决策层:通过比对系统自身信息库中的事实和数据,实时评估系统运行状态,判断各个故障自愈请求,并寻找出最优方案。自愈执行层:执行相关系统指令。免疫自愈层:处理整合自愈系统各模块的状态信息,制定各个自愈策略。
2.2 系统故障自愈的功能模块设计
基于人工免疫的自愈原理,本文设计了能够实现故障自愈的电液伺服系统,其工作流程如图6所示。电液伺服系统运行过程中信息处理模块对系统运行特征量进行特征提取与特征编码。自己/非己识别模块进行故障判断识别,并划分异常危险等级。若为已知抗原,固有免疫模块进行抗原-抗体匹配,执行对应自愈策略,系统状态评估为正常运行后,结束自愈流程;若为未知抗原,进行适应性免疫应答,进行免疫学习、记忆,更新系统数据信息库。
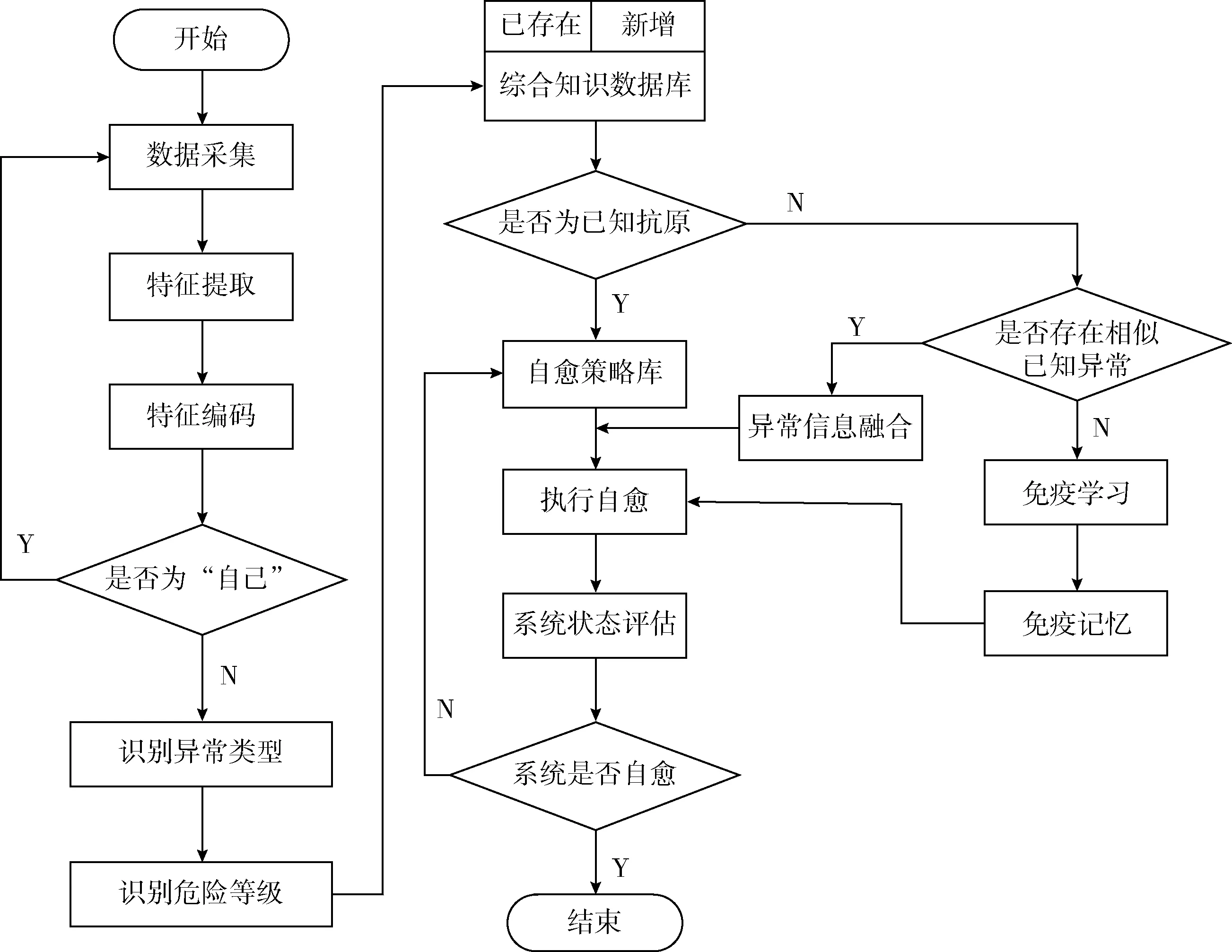
图6 故障自愈系统流程
(1)数据采集及特征量提取与编码
本设计中的信息处理模块,目的是采集、提取电液伺服系统运行过程中的状态参数,并且对状态特征量进行有效编码。选取系统运行时的液压缸杆位移、液压缸活塞速度、液压缸1和2端口压力差、传感器输出信号作为状态特征量,分别表示为n1、n2、n3、n4,状态特征编码表示为s=(n1,n2,n3,n4)。
(2)故障异常识别
自己/非己识别模块需要识别区分出故障异常,通过电液伺服系统故障分析,采用二进制对电液伺服系统的正常与异常状态进行编码,见表1。
自己/非己识别模块需要通过已知数据生成检测器集来识别自己、非己。在AMESim软件搭建的电液伺服系统仿真实验模型中,采集得到了系统的故障数据,见表2。

表1 电液伺服系统状态编码

表2 放大器故障样本
利用系统可接受阈值,划分α的取值,对系统的现有故障进行故障等级划分。
放大器故障等级划分见表3。

表3 放大器故障等级划分
(3)数据信息库设计
故障自愈系统结构图和系统故障自愈工作流程图的设计,需要有关于已知故障的抗原库,以及包含相应自愈策略的抗体库。依据故障的严重等级划分,定义系统衰退度的编码为001、010、011、100。根据免疫应答模块中抗体的编码方式,记忆抗体的二进制编码为:类型码,衰退码,抗体编码。其中类型码用来匹配抗原中的故障类型,衰退码为衰退度的编码。抗体编码形式为:码段1,码段2,…,码段n。抗体编码作用是生成与调取相应的自愈策略,每个段码对应一个自愈策略。
3 实验仿真及分析
在AMESim-Matlab的联合仿真操作系统环境中,验证了故障自愈模型的可行性。在系统稳定运行后,用故障注入的方法引入故障进行仿真实验:维持其余运行条件不变,在500~600之间任意调节参数kp。
系统监测采集出的各状态特征量经过信息处理后,得到了检测的数据样本。放大器故障的监测状态量为(0.15000.66640.69430.31830.2049)。在Matlab/Si-mulink中,s函数用于调用故障自愈模型各模块的功能算法以及已设计好的各个数据库。通过液压缸活塞速度状态特征量,诊断出放大器故障,故障程度是较严重故障Ⅲ;其中抗原编码为(01 011 0.15000.66640.69430.31830.2049);抗体编码为(01 011 01)。
通过匹配抗原与抗体的编码,调用抗体库中相应的自愈策略,实现电液伺服系统的故障自愈。图7是故障恢复后的曲线。液压缸杆位移跟随系统的给定输入信号,因二者间存在一定的时间滞后性(允许范围内),二者的误差值较小,并最终为0。液压缸活塞速度曲线稳定,未出现明显震荡波动,系统运行状态较为稳定,系统液压缸杆位移最终稳定在0.2 m。
经过仿真实验验证,本文提出的基于免疫理论的故障自愈模型,在电液伺服系统的运行过程中能够完成对系统自己、非己的判断,并对可恢复故障实施相应的自愈调节动作,完成故障自愈。
4 结束语
本文主要研究了基于人工免疫理论的电液伺服系统故障识别与故障自愈调节,实现了放大器故障的识别与恢复。仿真实验结果表明,所设计的电液伺服系统的故障自愈模型的可行性和有效性。系统在无外界介入干预的情况下,自行准确地识别故障类型及严重程度,并调用适当的自愈策略,使系统从故障状态恢复到正常运行状态。其原理可以推广到相关机电装备的设计、制造与维修中,具有一定的理论价值和工程意义。
参考文献:
[1]Zhu Y,Jiang W L,Kong X D,et al.Study on nonlinear dynamics characteristics of electrohydraulic servo system[J].Nonlinear Dynamics,2015,80(1-2):723-737.
[2]Jiang W,Wei B,Xie C,et al.An evidential sensor fusion method in fault diagnosis[J].Advances in Mechanical Engineering,2016,8(3):1-7.
[3]Li Z,Peng T,Zhang P F,et al.Fault diagnosis and fault-to-lerant control of photovoltaic micro-inverter[J].Journal of Central South University,2016,23(9):2284-2295.
[4]Gao Z,Cecati C,Ding S X.A survey of fault diagnosis and fault-tolerant techniques—Part I:Fault diagnosis with model-based and signal-based approaches[J].IEEE Transactions on Industrial Electronics,2015,62(6):3757-3767.
[5]Tanha M,Hashim F,Subramaniam S.Secure and self-healing control centers of critical infrastructures using intrusion tole-rance[J].International Journal of Network Security,2015,17(4):365-382.
[6]Schneider C,Barker A,Dobson S.Evaluating unsupervised fault detection in self-healing systems using stochastic primitives[J].EAI Endorsed Transactions on Self-Adaptive Systems,2015,1(1):e3.
[7]Yuan L,Man M,Chang X.Principles of electromagnetic protection bionics and research of fault self-recovery mechanism[J].Engineering,2014,12(3):83-96.
[8]FENG Yongbao,LIU Jie,LI Rong,et al.Research on mo-deling and simulation of vectoring nozzle electro-hydraulic servo system based on AMESim /MATLAB co-simulation[J].MATLAB Machine Tool and Hydraulic Technology,2015,43(4):118-121(in Chinese).[冯永保,刘杰,李荣,等.基于AMESim与MATLAB的矢量喷管电液伺服系统建模与仿真研究[J].机床与液压,2015,43(4):118-121.]
[9]LI Bo,CHEN Jun,ZHANG Weiming,et al.Research status of electro-hydraulic servo system modeling, identification and control[J].Machine Tool and Hydraulics,2016,44(13):168-172(in Chinese).[黎波,陈军,张伟明,等.电液伺服系统建模、辨识与控制的研究现状[J].机床与液压,2016,44(13):168-172.]
[10]Grossschmidt G,Harf M.Multi-pole modeling and simulation of an electro-hydraulic servo-system in an intelligent programming environment[J].International Journal of Fluid Power,2015,17(1):1-13.
[11]Liu H,Liu D,Lu C,et al.Fault diagnosis of hydraulic servo system using the unscented Kalman filter[J].Asian Journal of Control,2015,16(6):1713-1725.
[12]MI Shuangshan,FU Jiuchang,HAN Cui’e.Application of AMESim in hydraulic system fault simulation[J].Machine Tool and Hydraulics,2013,41(11):183-186(in Chinese).[米双山,付久长,韩翠娥.AMESim在液压系统故障仿真中的应用[J].机床与液压,2013,41(11):183-186.]
[13]SUN Jingjie,ZHAO Jianjun,YANG Libin,et al.Application of an artificial immune classifying method in fault diagnosis[J].Computer Engineering,2013,39(8):208-214(in Chinese).[孙靖杰,赵建军,杨利斌,等.一种人工免疫分类方法在故障诊断中的应用[J].计算机工程,2013,39(8):208-214.]

