粉料干法造粒挤压辊的力学特性及有限元分析

刘志民 韩 雷 刘 洋

(河北工程大学机械与装备工程学院，河北 邯郸 056038)

干法造粒是在湿法造粒基础上发展而来的一种新型造粒工艺，其工艺流程是将物料粉末连续挤压成型、造粒，物料中无需添加任何粘合剂，生产过程环保、高效。同时干法造粒具有改进产品外观，改善分离状原料的流动特性，便于贮存和运输，方便准确定量，减少粉末飞尘污染等优点，在制药、化工、食品等工业生产领域应用广泛[1-2]。

挤压辊是干法造粒工艺过程中的关键工作部件，松散物料在挤压螺旋喂料压力作用下，依次经过两相向匀速旋转挤压辊之间的滑动区和咬入区，物料在滑动区内与挤压辊之间的相互作用力较小，随着挤压辊连续旋转，物料进入咬入区且体积被逐渐压缩，物料与挤压辊之间的相互作用力也随之增大，当物料进入两挤压辊中心线最小间隙附近时，物料被挤压成密实状薄片，此时，物料与挤压辊之间的作用力达到最大值[3-7]。物料与挤压辊间的最大作用力及挤压辊的受力变形对物料成形的密实度和系统工艺过程控制有着重要影响，其结果将直接影响造粒效果和质量。为此，本研究根据Von Mises准则[8]，将理论分析与有限元仿真方法相结合，分析挤压辊受力特性和变形规律，此研究为干法造粒机挤压辊的优化提供理论设计依据，同时也为干法造粒挤压系统的过程控制提供参考。

1 挤压辊力学模型及受力分析

在实际干法造粒工艺生产过程中，物料对挤压辊的作用力为径向方向，当忽略泊松比所引起的挤压辊沿轴线方向滑动时，挤压辊力学模型(见图1)可简化为平面应变问题。物料在挤压螺旋喂料压力P0[9-10]和挤压辊压力共同作用下，依次经过滑动区和咬入区，两挤压辊在平面应力场受到的作用力对称分布，故仅在其中一个挤压辊内部建立坐标系(x,z)，表面作用力所引起的应力分量可按Jonhson[11-13]给出的公式进行计算：

(1)

式中：

x、z——挤压辊中任意一点坐标，mm；

σx、σz、τxz——平面内应力分量，Pa；

p(s)——挤压辊接触表面上的表面压力，Pa；

q(s)——挤压辊接触表面切向力，Pa；

α——咬入角α所对弧面长度，mm；

s——接触表面上任意一点至接触中心的距离，mm。

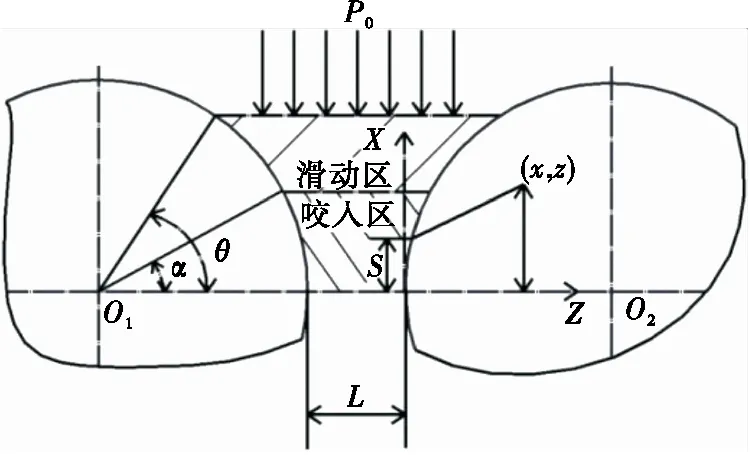
图1 挤压辊力学模型

咬入区内表面压力p(s)根据Johanson等[14-15]给出的公式进行计算，则挤压辊任一位置角θ处的平均压力值σθ按式(2)计算：

(2)

式中：

σα——当θ=α时的平均应力，Pa；

K——物料压缩系数，当物料在一定的含水量和温度情况下为特定常数；

L——挤压辊间隙，mm；

D——挤压辊直径，mm；

d——挤压辊表面沟槽深度，mm。

由于咬入角α随物料属性和挤压条件等因素而变化，无法从理论上测出精确数据，而物料在咬入区内受到连续挤压作用时，其单位厚度质量会保持不变，仅密度发生变化，因此，咬入角α可按式(3)进行估算：

cosα=1-L(γ′-γ)/Dγ，

(3)

式中：

γ——物料松装密度，g/cm3；

γ′——物料压实密度，可通过试验进行估算，g/cm3。

将式(3)代入式(2)，当取位置角θ=0时，可计算出咬入区内挤压辊接触表面最大压力σθ=0，此压力数值即为咬入区内挤压辊接触表面上任意一点至接触中心距离为0时的最大表面压力p(0)。由于咬入区内物料与挤压辊表面没有相对滑移，故切向力q(s)=0，并用m和n表示挤压辊内一般点(x,z)处的应力，则挤压辊平面内任意一点应力分量计算公式[式(1)]可简化为：

(4)

m和n由式(5)定义，且式中m和n的正负号分别与z和x处坐标正负号一样：

(5)

在平面内任意一点应力状态可以用4个应力分量进行描述，即σx、σz、τxz、σy，其中，σy是沿着挤压辊轴线方向的应力，也是平面内任意一点的中间主应力，其大小根据公式σy=ν(σx+σz)进行确定。取挤压辊弹性参数泊松比ν=0.3，则Von Mises等效应力为：

(6)

将式(4)、(5)代入式(6)，并分别对Von Mises等效应力σeq、咬入角α所对弧面长度a、坐标x和坐标z进行无量纲化处理，得到挤压辊不同深度横截面z/a处无量纲等效应力σeq/p(0)随无量纲坐标x/a变化曲线见图2。从图2可以看到，在不同深度圆柱面无量纲等效应力沿两挤压辊连心线呈对称分布，且在x/a=0.0(咬入角α为0)处出现极大值。在z/a=0时的挤压辊表面，无量纲等效应力最小，且保持为一常量；当z/a=1.0(挤压辊深度为a圆柱面)时，无量纲等效应力最大，但在x/a=0.0处应力幅值变化较小；当z/a=0.5(挤压辊深度为0.5a圆柱面)时，无量纲等效应力较大，且在x/a=0.0处应力幅值变化最大。说明在横截面z/a=0.5时，应力沿挤压辊接触面中心附近幅度变化最大。此分析结果与Von Mises准则描述相一致，即当摩擦系数较小时，屈服首先会出现在接触体内部。

图2 无量纲等效应力相对于无量纲坐标x/a 的分布曲线

Figure 2 The distributing curves of the dimensionless stress with respect to the dimensionless coordinatesx/a

2 挤压辊有限元仿真分析

为进一步定量研究挤压辊的力学特性，利用ANSYS Workbench软件对其进行仿真分析。

2.1 挤压辊有限元模型建立

利用SolidWorks软件建立挤压辊三维实体模型，选取挤压辊工作面直径为240 mm，见图3。点击SolidWorks软件中的ANSYS Workbench接口选项，将三维实体模型导入ANSYS Workbench软件中，右击Mesh选项，结合挤压辊回转体结构特点，选择Sweep选项对挤压辊模型进行扫掠法六面体单元网格划分，见图4。最后对挤压辊有限元模型进行参数设置，材料选择Mn13，其泊松比为0.3、弹性模量为2.06×105MPa、密度为8 900 kg/m3，屈服强度为800 MPa。

图3 挤压辊模型

图4 挤压辊网格划分

2.2 施加载荷和边界约束

右击static structural选项，在挤压辊轴承两端添加约束，一端轴承作用面限制x，y，z自由度，另一端轴承作用面限制y，z自由度。在挤压成型过程中，松散物料在挤压螺旋喂料压力、挤压辊匀速旋转带动和挤压辊压力共同作用下，物料与挤压辊表面紧密接触，咬入角内挤压辊受到的作用力是均匀分布的，由式(2)计算面载荷为54.1 MPa。通过Geometry模块，在挤压辊和物料接触表面添加印记面，施加面载荷压力为54.1 MPa。

2.3 结果求解与分析

载荷和边界约束添加完成后，在solution选项中右击Solve命令开始运算求解。求解完成后，通过Deformation选项提取挤压辊变形云图，见图5，发现挤压辊变形最大的地方为挤压过程中与物料直接接触的表面，并且在挤压辊与物料接触的中心表面呈椭圆形分布，通过提取变形量数据，绘制距挤压辊表面不同深度的变形曲线见图6。变形主要集中在沿挤压辊中心轴向长度30～150 mm内，且最大变形量出现在挤压辊表面z/a=0.0中心区域，变形量达0.026 4 mm，随着深度增加其变形量逐渐减小，在挤压辊深度z/a=0.5时变形量为0.018 8 mm，在挤压辊深度z/a=1.0时变形量为0.011 6 mm。

通过Equivalent Stress选项提取挤压辊应力云图(见图7)，提取挤压辊中心断面和两端面径向应力分布，绘制不同截面径向应力分布曲线(见图8)，发现应力极值出现在与物料接触的挤压辊表面以下深度40 mm，最大应力为43.2 MPa，并在端面过渡部分出现应力集中。提取挤压辊z/a为0.0，0.5，1.0时不同深度应力数据，绘制挤压辊不同深度应力曲线见图9，发现在横截面z/a为1.0，0.5时应力大于挤压辊表面z/a=0.0的应力，即与上述无量纲等效应力相对于无量纲坐标x/a变化曲线相一致。

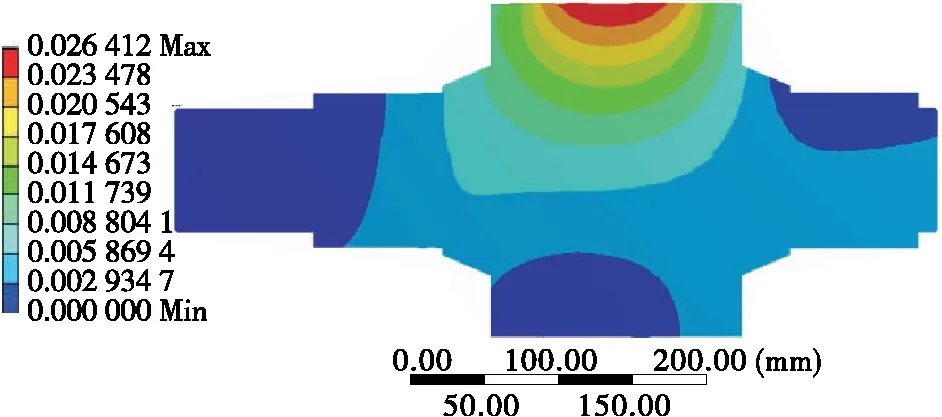
图5 挤压辊变形云图

图6 挤压辊变形曲线

图7 挤压辊等效应力云图

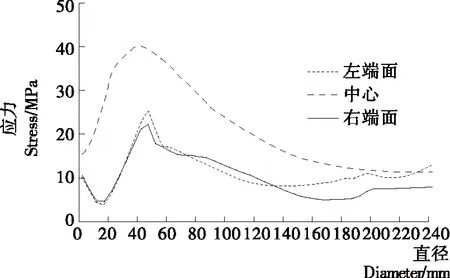
图8 挤压辊径向应力曲线

图9 挤压辊应力曲线

3 结论

(1) 挤压辊力学特性理论分析与有限元结果仿真与Von Mises准则描述相一致，且有限元仿真给出了挤压辊应力及变形程度的定量评价。

(2) 挤压辊变形主要集中在沿挤压辊宽度30～150 mm内，最大变形量出现在挤压辊表面(z/a=0.0)中心区域，变形量达0.026 4 mm，且随着深度增加其变形量逐渐减小。

(3) 挤压辊在深度z/a=0.5横截面应力最大，与实际情况是一致的；同时，为避免挤压辊端面与轴过渡部分在z/a=0.5横截面附近出现应力集中，可进一步对挤压辊结构进行优化设计。

[1] 彭飞, 李腾飞, 康宏彬, 等. 小型制粒机喂料器参数优化与试验[J]. 农业机械学报, 2016, 47(2): 51-58.

[2] 王善荣. 大麦压片机的研制[J]. 食品与机械, 1997(5): 25-26.

[3] PATEL B A, ADAMS M J, TURNBULL N, et al. Predicting the pressure distribution during roll compaction from uniaxial compaction measurements[J]. Chemical Engineering Journal, 2010, 164(2/3): 410-417.

[4] 李欣, 王国强. 高压辊磨机磨辊强度有限元分析[J]. 建筑机械, 2003(9): 45-48.

[5] BINDHUMADHAVAN G, SEVILLE J P K, ADAMS M J, et al. Roll compaction of a pharmaceutical excipient: Experimental validation of rolling theory for granular solids[J]. Chemical Engineering Science, 2005, 60(14): 3 891-3 897.

[6] MAOUCHE N, MAITOURNAM M H, VAN K D. On a new method of evaluation of the inelastic state due to movingcontact[J]. Wear, 1997, 203-204(96): 139-147.

[7] 张鹏. 辊压造粒机压辊分离力的近似计算[J]. 中国井矿盐, 2003(5): 37-38.

[8] 冯剑军, 谭援强. 基于Hertz理论圆柱和平面之间的滑动接触分析[J]. 摩擦学学报, 2009, 29(4): 346-350.

[9] 陈传文. 粉料充填系统计量误差的因素与控制[J]. 食品与机械, 1994(3): 20-20.

[10] 孙晓霞, 孟文俊, 梁志坚, 等. 基于TCP流稳定螺旋涡的垂直螺旋输送机的设计方法[J]. 北京理工大学学报, 2017, 37(11): 1 114-1 121.

[11] JOHANSON K L. 接触力学[M]. 徐秉业, 译. 北京: 高等教育出版社, 1992: 20-21.

[12] KOGUT L, ETSION I. Elastic-plastic contact analysis of a sphere and a rigidflat[J]. Journal of Applied Mechanics, 2002, 69(5): 657-662.

[13] HUI Qiu, HILLS D A, NOWELL D, et al. Skew sliding of an elastic cylinder: An investigation of convection in contact[J]. International Journal of Mechanical Sciences, 2008, 50(2): 293-298.

[14] JOHANSON J R. A rolling theory for granularsolids[J]. Journal of Applied Mechanics, 1965, 32(4): 842.

[15] MULIADI A R, LITSTER J D, WASSGREN C R. Modeling the powder roll compaction process: Comparison of 2-D finite element method and the rolling theory for granular solids (Johanson’s model)[J]. Powder Technology, 2012, 221: 90-100.