基于量子柔性表示的图像边缘提取算法

张姗姗，曹 琨，朱志琨

(1.河南牧业经济学院 软件学院，河南 郑州 450000；2.北京航空航天大学 计算机学院，北京 100191)

0 引 言

随着图像传感器的发展，图像的数量越来越庞大，图像边缘检测与提取的准确性和快速性遇到了较高的挑战，成为图像处理研究的热点之一[1,2]。

基于Sobel算子的图像边缘提取技术[3]主要是根据相邻像素点灰度加权差计算，在边缘处处于极值这一特性进行判断，对噪声具有较好的平滑处理，计算简单、速度迅速。能够获得准确的边缘方向，但其准确性不高。张闯等[4]提出一种基于欧氏距离图的图像边缘提取技术，通过欧氏距离能够降低“背景”的影响，可以较好地提高图像边缘灰度，但该算法对弱边缘提取效果不太理想，容易出现边缘漏检和误检的现象，主要是其没有考虑不同位置的像素对于中心的影响。贾迪等[5]提出了一种基于高斯距离加权图的边缘提取算法，该方法通过计算区域内像素间的高斯加权距离获得距离图，使边缘突出并弱化背景，从而获得了“背景”和“边缘”两种灰度。根据距离图的直方图，并作为改进CV模型的参数，利用CV模型捕抓边缘。

近年来，量子计算和数字图像处理的合并在处理高准确性和高实时性问题的实际图像处理应用程序中已被证明是富有成果的。例如，Tseng等[6]提出了基于Sobel算子耦合量子晶格算法，但是其性能没有得到提升。Fu等[7]提出了一种基于模糊熵理论提取边缘提高量子晶格图像，该算法可以显示更弱的边缘，并有较好的噪声鲁棒性，但是其仍无法解决计算复杂性过大问题。在量子图像中，每一个像素的位置信息被存储为一个二维量子比特序列的基态，颜色信息存储在一个量子比特的概率幅，如图1所示显示了一个4*4大小的量子图像。

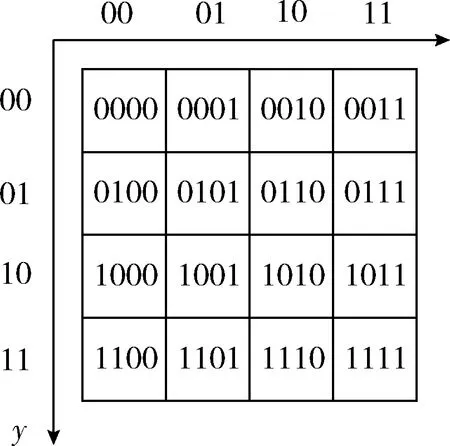
图1 大小为4*4的FRQ图像

图像边缘提取是数字图像处理中的一个重要问题，在图像中，边缘是图像的颜色强度具有不连续性的像素，基于这一特性，为了找到所有的不连续像素，所有经典算法都需要分析和计算每个像素的图像强度梯度。因此，对于一幅2n×2n图像，其计算复杂度都大于O(22n)，随着图像数据急剧增加，传统的算法在图像边缘提取中实时性问题越来越严重。因此，为了提高算法效率和边缘质量，降低噪声敏感度，本文提出了一种基于量子柔性表示的图像边缘提取方法。通过量子柔性表示图像，利用量子序列的叠加态来存储图像的所有像素，通过量子并行计算显著提高效率，得到量子FRQ图像，再对得到FRQ图像进行X和Y方向的平移变换，获得整个图像的邻域像素的相对量子，然后，根据邻域像素的量子比特定义量子黑盒UΩ，结合Sobel算子计算像素的Sobel梯度，通过Sobel梯度判断不同类别的像素并提取图像的边缘。最后，通过实验验证了提出算法的性能。

1 Sobel算子

在本节中，简要介绍了经典的Sobel边缘提取算法[1,8]。掩模计算是Sobel中一种常见的技术，能够计算每个像素的图像强度的梯度。图2(a)描绘了像素邻域窗口。Sobel使用掩模显示在图2(b)和图2(c)中计算导数的两个近似值，一个用于水平变化，一个用于垂直变化。首先，Sobel算子将分别得到的X轴和Y轴的导数近似。如式(1)所示，Gx和Gy表示如何利用掩模来计算两个衍生物。式(2)给出了梯度g与两个导数的关系。通过与梯度阈值T比较。

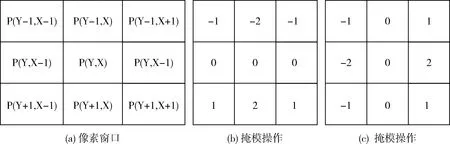
图2 Sobel算子掩模

当g≥T时，该像素将被视为边缘的一部分

Gx= (p(Y+1，X+1)+2p(Y+1,X)+p(Y+1,

X-1))-(p(Y-1,X+1)+2p(Y-1,X)+

p(Y-1,X-1))

(1)

Gy= (p(Y+1，X+1)+2p(Y,X+1)+p(Y-1,

X+1))-(p(Y+1,X-1)+2p(Y,X-1)+

p(Y-1,X+1))

(2)

主程序是计算每个像素的强度梯度使用Sobel掩模。因为每个像素都需要处理，对于一幅大小为2n×2n的图像，Sobel算法的计算复杂性为O(n2)。类似于Sobel，其它经典的边缘提取算法，利用不同的掩模或方法计算的强度梯度近似。因此，一幅大小为2n×2n的图像，当前的边缘提取算法的复杂度一般超过O(n2)。

2 本文图像边缘提取算法设计

针对当前的边缘提取算法的实时性问题，提高边缘连边缘的完整性和清晰度，提出了一种基于量子柔性表示的边缘提取方法，主要步骤如下：

(1)首先，利用量子柔性表示将数字图像量化为量子图像，为了存储量子图像，需要2n+1量子寄存器，为下一步的操作需要额外的比特存储所有像素点的邻域像素的颜色信息，表示如下

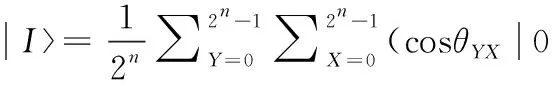
(3)

(2)进行掩模计算，在掩模计算中，经过第1步到第8步后，得到整个图像的邻域像素的相对彩色量子比特并将它们存储到一个额外的比特，在这一步的主要操作是X轴向平移和Y平移变换。

(3)当对3×3邻域窗口中的8个彩色量子储存后，利用设计的量子黑盒UΩ来计算所有像素的Sobel梯度，并将结果存储到另一个量子比特|Ω(Y,X)中，通过量子比特序列构建一个新的量子图像。

类似Sobel算子，在量子图像中，边缘像素的彩色量子为|1，表示白色；相反，非边缘像素的彩色量子为|0，表示黑色。因此，通过计算判断了不同类别的像素并提取了量子图像的边缘。

2.1 X和Y平移变换

根据式(3)得知，FRQ模型保持二维像素矩阵，因此，如果改变整个图像，每个像素将同时访问其邻域的信息，例如，使一图像向下移动一个单位，该像素将从P(Y，X)到转换为P(Y-1，X)。

对此，两个平移定义如下：

定义1U(x±)：基于大小为2n×2nFRQ图像的沿X方向的平移变换，定义如下

U(x±)|I|Y|(X±1)mod2n

(4)

通过利用X代替X±1可变换表示

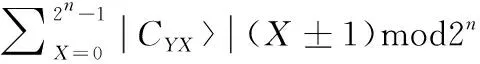
(5)

其中，X′=(X∓1)mod2n，表示为

U(x±)|I

(6)

类似地，Y平移变换表示为：

定义2U(y±)：基于大小为2n×2nFRQ图像的沿X方向的平移变换，定义如下

U(x±)|I

(7)

同理，通过利用Y代替Y±1可变换如下表示

(8)

其中，Y′=(Y∓1)mod2n。因此，图像中的所有像素可以在Y轴和Y平移变换中达到各邻域像素。图3给出了8×8大小图像的转换U(x+)的例子。所以，所有像素可通过在平移下达到和其它像素一致。

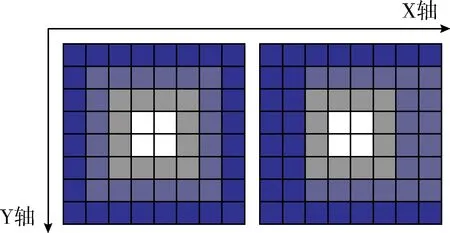
图3 U(x+)图像变换

2.2 单一性

表1描绘了不同的操作和变换矩阵的U(x+)的在不同宽度的X轴的图像。从表1中，可以得出这样的结论：当利用n个量子位存储像素的X轴上的信息，U(x+)将为n长度量子序列进行循环移位操作。其变换矩阵如下所示

(9)

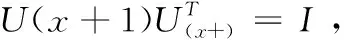
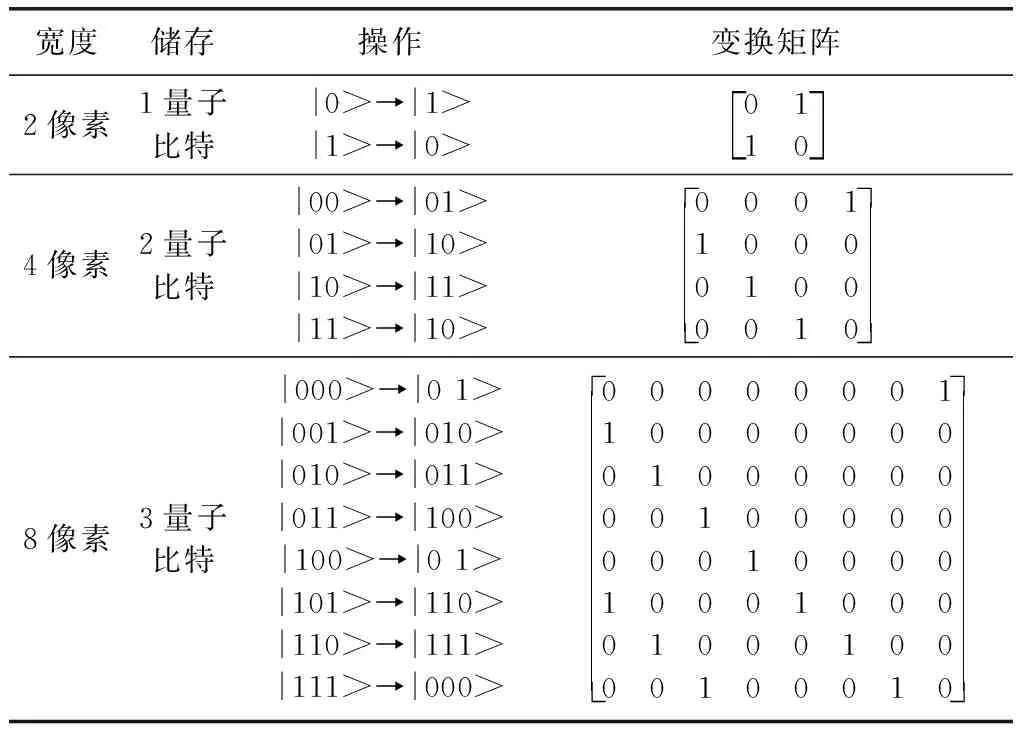
表1 在X轴下图像不同宽度的操作和变换的矩阵U(x+)

2.3 复杂度计算

为了计算n长度量子序列的变换U(x+)的计算复杂度，每一个任意的多量子量子的操作可以分解为若干个单量子量子门、2量子门和3量子门。一般来说，可通过这些简单的量子门的数量来表示的量子运算的计算复杂度的估计[9]。对于一幅2n×2n的图像，x轴方向的展示可表示为

|x=|xn-1xn-2…x1x0

(10)

因此，U(x+)可分解为如下表示

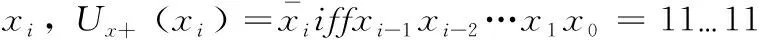
(11)

因此，这意味着在量子量子序列的每量子将被所有的量子量子的支配，图4给出了详细的U(x+)变换为n长度量子序列的量子电路。

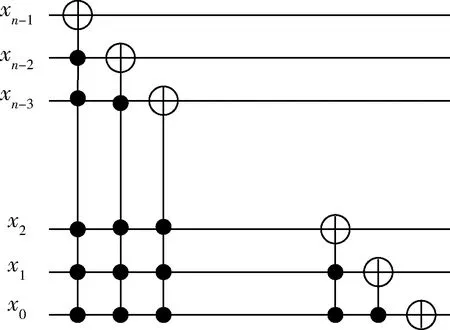
图4 U(x+)变换为n长度量子序列的量子电路

从图4看出，当将U(x+)变换为一个n长度的量子序列时，实际操作可以分解成n个步骤，并在第k步子操作处理k量子。在量子电路中，x0需要一个单一量子反转门，因为在平移过程中没有任何控制而反转。然而，xk在k控制的非门，形成了k+1量子门。通过图4中的量子电路的分析得知，如果只使用单粒子翻转门，2量子比特门，和3量子比特Toffoli门构建整个电路的改造U(x+)的信息，需要一个单量子翻转门，一个2量子比特门，和一些量子的Toffoli 门。3位量子-Toffoli门的总数如下[10]

(12)

通过以上分析可得出，U(x+)变换为一个长度为n的量子序列计算复杂度不超过O(n2)。

2.4 掩模计算

根据以上描述，利用上述两种平移变换，根据Sobel掩模和邻域窗口计算图像中像素的强度梯度。图2(b)和图2(c)显示了Sobel掩模，为了获得每个像素的强度梯度，需要利用掩模来计算3×3窗口的近似的梯度，在一定的顺序的平移变换可获得每个像素的邻域窗口的颜色信息，详细计算如下表示：

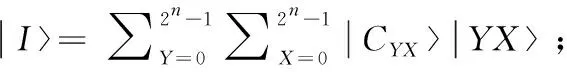
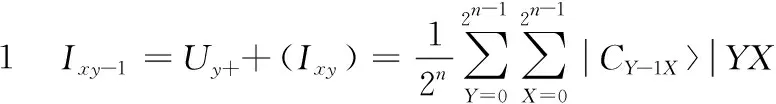
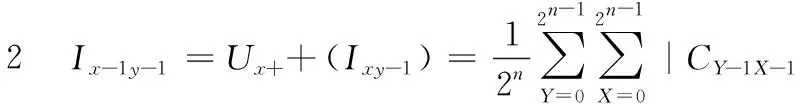
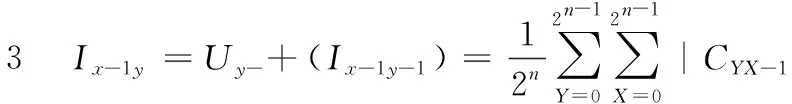
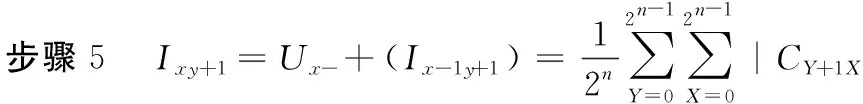
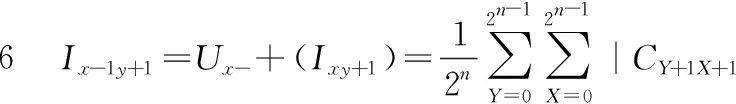
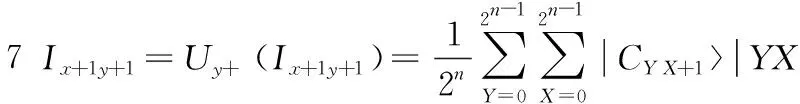
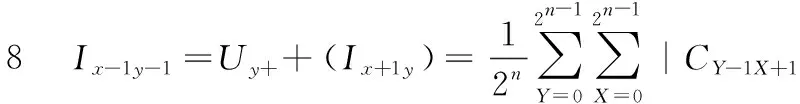
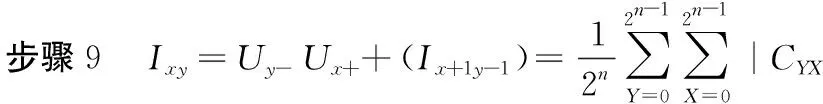
根据上述计算步骤中可看出，经过步骤1到步骤8后，平移操作可得到各像素邻域像素的颜色信息，共有6个Y移位操作和4个X轴向移动操作，因此，计算的复杂度为O(n2)。

为了计算所有像素的图像强度的近似梯度，设计一个量子黑盒UΩ，利用相邻像素的彩色量子，图5显示了量子黑盒UΩ组成。

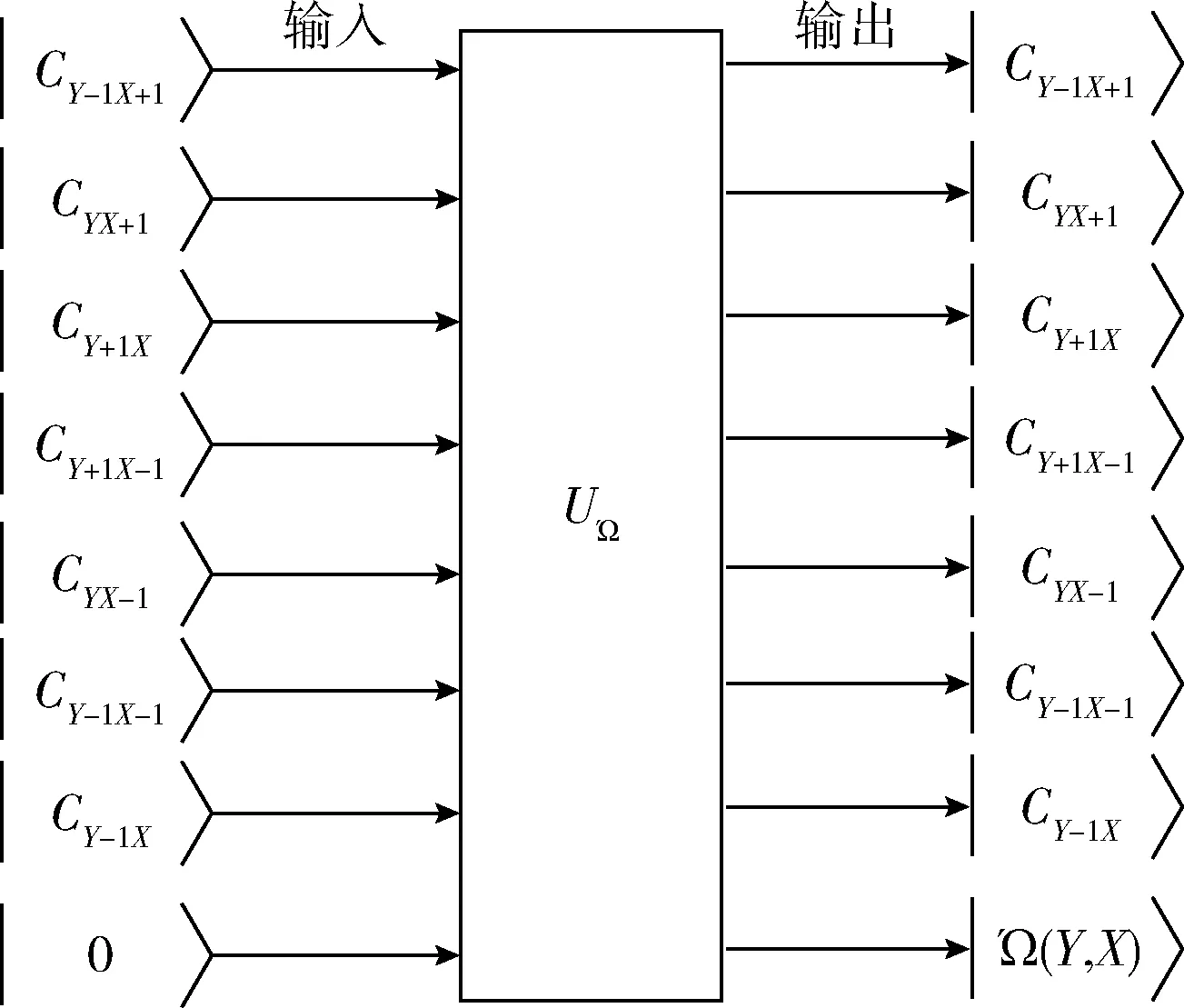
图5 量子黑盒结构

在UΩ中，其工作关系表示如下

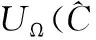
(13)

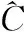
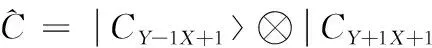
|CYX-1⊗|CY-1X-1⊗|CYX-1⊗|CY-1X

(14)

|Ω(Y,X)

(15)

其中，Gx(i,j)和Gy(i,j)分别为x方向，y方向的导数逼近，定义如下

Gx(Y,X)= (CY-1X-1+2CYX+1+CY+1X+1)-

(CY-1X-1+2CYX-1+CY+1X-1),

(16)

Gy(Y,X)= (CY+1X-1+2CY+1X+CY+1X+1)-

(CY-1X-1+2CY-1X+CY-1X+1),

(17)

通过量子黑盒UΩ运算，完成了所有像素的Sobel梯度计算，并储存在彩色量子|Ω(Y,X)中，根据量子序列的位置形成一个新的结果图像，类似与经典的Sobel算法，在新的结果图像中，所有像素的彩色量子在边缘中为|1，表示为白色，反之其它像素的彩色量子为|0，表示为黑色。

3 实验与讨论

为了对提出的算法性能的进行验证，进行不同的实验测试。仿真环境为：Core I3-4150 CPU，3.50 GHz，8 GB运行RAM，Win7操作系统，并借助MATLAB7.0进行仿真分析。为体现本文算法的先进性，选取当前常用的图像边缘提取算法文献[3-5]作为对照。

3.1 评价指标

为了更加准确测量和评价提出算法的性能，采用信噪比(SNR)和Baddeley误差测量(Baddeley error metric，BED)作为评价指标。SNR定义如下[11]

(18)

其中，Imean为灰度值，σI为标准差，SNR越高越好。

假设I1和I2是大小均为N×M的两个图像，并且p={1,…,N}×{1,…,M}作为该位置的集合，则BED定义如下[12,13]

(19)

其中，g用于加权的递增函数，同时定义d(p,Ii)为位置p和最接近边缘点Ii之间的距离。

3.2 实验结果

图6，图7为本提取算法的两组实验结果。图6(a)为一幅袋鼠图像，图6(b)～图6(e)分别为文献[3-5]和本文算法得到的边缘结果。图6(b)～图6(c)中突出了袋鼠的大体轮廓边缘，但是忽略了图像背景中的细节目标，对弱边缘提取能力较差，边缘连续性不足；图6(d)相对于图6(b)～图6(c)具有一定的提高，在突出主体边缘的同时也能捕抓一些局部细节边缘，但是提取的边缘出现一些间断现象；图6(e)中为本文算法得到的结果，从图中看出本文算法性能相对于前3种算法具有一定的改善，能够较好提取目标轮廓边缘和细节信息边缘，并且得到的边缘连续性好。

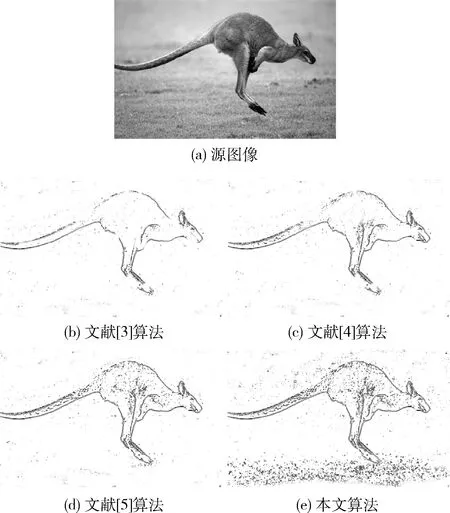
图6 袋鼠图像边缘提取结果

图7(a)为一幅花朵图像，图7(b)～图7(e)分别为文献[3-5]算法和本文算法得到的边缘结果。图7(b)～图7(c)中显示了花朵的花瓣和叶子的主要边缘，但是对叶子中的纹理和一些阴影部分边缘提取结果不太理想，边缘连续性不太理想；图7(d)相对于图7(b)～图7(c)具有一定的改善，在突出花瓣和叶子边缘的同时也能捕抓一些局部细节边缘，但是提取的边缘出现一些间断现象；图7(e)中为本文算法得到的结果，从图7中可得出本文算法提取的边缘最优，能够较好提取花瓣和叶子边缘，边缘连续性好。

图7 花朵图像边缘提取结果

为了进一步分析边缘提取算法性能，通过添加不同高斯噪声进行测试，噪声大小为均值为0，方差为(0，5，10，15，20，25，30)。图8为均值为0，方差为10得到的边缘结果。图8(a)为一幅含有噪声方差为10建筑图像，图8(b)～图8(e)分别为文献[3-5]算法和本文算法得到的边缘结果。图8(b)～图8(c)中建筑图像的边缘提取效果不太理想，遗漏了许多重要边缘，得到的边缘不连续。图8(d)相对于图8(b)～图8(c)具有一定的提高，突出了建筑物和树边缘，对建筑的窗口和图案边缘具有一定的效果。但是由于噪声的存在，将某些噪声点误提取为边缘边，影响边缘提取的准确性。图8(e)中为本文算法得到的结果，从图8中可得出，在含有噪声情况下，本文算法提取的边缘效果较好，能够清晰地反映出建筑物的轮廓边缘，较好的剔除了噪声点的影响，并且对于建筑物中的图案和字体边缘也体现了，很好地消除了噪声的干扰。

图8 建筑物图像边缘提取结果

为了准确测量噪声对算法的影响，在不同噪声下测量算法得到的边缘图像，并进行定量评价。图9为在噪声大小为均值为0，方差为(0，5，10，15，20，25，30)的高斯噪声下测量的SNR和BED的测量结果。根据图9中看出，在不同的噪声方差下的对所提取的边缘结果会有一定的影响，但是从曲线图中可看出，文献[3-5]算法受噪声的影响较大，而本文算法随着噪声的变化相对影响较少。

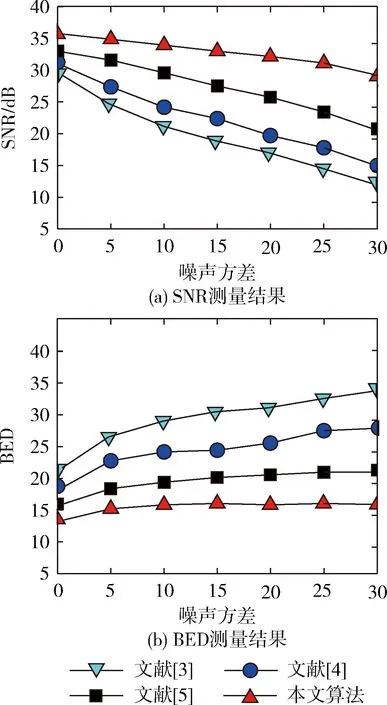
图9 不同噪声下测量的SNR与BED结果

根据以上实验结果与评价指标的定量测量得出，本文算法能够有效提取完整的图像的边缘，并且提取的边缘包含了详细的信息，边缘连续性较好。而对照组算法中出现了较多的边缘的漏检和误检现象，提取的边缘连续性不太理想，主要原因本文算法中采用了量子柔性表示，利用量子序列的叠加态来存储图像的所有像素，得到量子柔性表示FRQ图像，通过结合Sobel算子计算像素的Sobel梯度，根据Sobel梯度判断不同类别的像素并提取图像的边缘，从而有效提高了边缘提取的精度。而文献[3]算法中Sobel算子定位精度不够理想。文献[4]算法中由于没有考虑不同位置的像素对中心区域的影响，对弱边缘和噪声提取效果不佳。文献[5]算法中对于背景和轮廓不能很好识别，对同质区域边缘检测效果有所降低。

3.3 复杂性测试

为了评价算法效率，对算法的运算时间进行测量。表2给出了不同图像在不同算法下的耗时对比，文献[3]算法由于处理方法简单，速度最快。文献[4]算法和文献[5]算法中由于需要计算每个像素和邻域像素，导致其耗时较高，图像尺寸越大，其消耗时间越长。但是本文算法的运行时间较少。主要是因为本文算法利用量子序列的叠加态来存储图像的所有像素，通过量子并行计算显著提高效率，降低了算法处理时间。

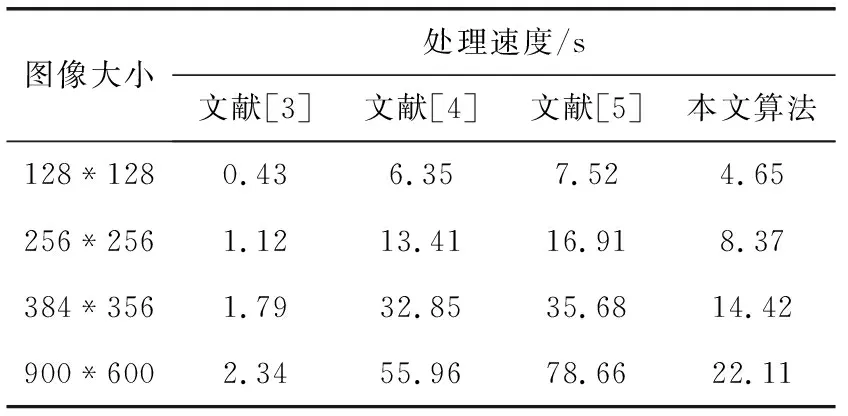
表2 算法处理时间对比

4 结束语

采用了量子柔性表示对图像进行量化，结合Sobel算子的特性，本文提出了一种基于量子柔性表示的边缘提取算法。将图像进行量子柔性表示，利用量子序列的叠加态来存储图像的所有像素，通过量子并行计算显著提高效率，得到FRQ图像。对得到FRQ图像进行X和Y方向的平移变换，获得整个图像的邻域像素的相对量子，再根据邻域像素的量子比特定义量子黑盒UΩ，结合Sobel算子计算像素的Sobel梯度，通过Sobel梯度判断不同类别的像素并提取图像的边缘。通过实验结果验证了提出的算法具有较快的边缘提取速度，能够有效提取完整的边缘信息，降低了噪声干扰，并且较好保持了边缘的连续性和完整性，为后续图像处理提供了帮助。

参考文献：

[1]XIA Qing,ZHANG Zhenxin,WANG Tingting.Edge extraction algorithm of on improved infrared thermal image based Sobel operator[J].Laser & Infrared,2013,43(10):1158-1162(in Chinese).[夏清,张振鑫,王婷婷.基于改进Sobel算子的红外图像边缘提取算法[J].激光与红外,2013,43(10):1158-1162.]

[2]Swaminathan A,Ramapackiyam SSK.Edge detection for illumination varying images using wavelet similarity[J].Let Image Processing,2014,8(5):261-268.

[3]YUAN Chunlan,XIONG Zonglong,ZHOU Xuehua.Study of infrared image edge detection based on Sobel operator[J].Laser & Infrared,2013,39(1):85-87(in Chinese).[袁春兰,熊宗龙,周雪花.基于Sobel算子的图像边缘检测研究[J].激光与红外,2013,39(1):85-87.]

[4]ZHANG Chuang,WANG Tingting,SUN Dongjiao,et al.Image edge detection based on the Euclidean distance graph[J].Journal of Image and Graphics,2013,18(2):176-183(in Chinese).[张闯,王婷婷,孙冬娇,等.基于欧氏距离图的图像边缘检测[J].中国图象图形学报,2013,18(2):176-183.]

[5]JIA Di,MENG Xiangfu,MENG Lu.Image edge extraction combined with a Gaussian weighted distance graph[J].Journal of Image and Graphics,2014,19(1):62-68(in Chinese).[贾迪,孟祥福,孟琭.结合高斯加权距离图的图像边缘提取[J].中国图象图形学报,2014,19(1):62-68.]

[6]Tseng C,Hwang T.Quantum digital image processing algorithms[C]//Proceedings of the 16th IPPR Conference on Computer Vision,Graphics and Image Processing,2003:827-834.

[7]Fu X,Ding M,Sun Y,et al.A new quantum edge detection algorithm for medical images[J].Proceedings of Medical Imaging, Parallel Processing of Images and Optimization Techniques,2016,28(6):749-758.

[8]SUN Qiucheng,HOU Yueqian,TAN Qingchang.A sub-pixel edge detection method based on an arctangent edge model[J].Optik-International Journal for Light and Electron Optics,2016,51(15):459-468.

[9]Zhang Y,Lu K,Gao Y,et al.NEQR:A novel enhanced quantum representation of digital images[J].Quantum Inf Process,2013,12(7):2833-2860.

[10]CHENG Xueyun,GUAN Zhijin,ZHANG Haibao.Rule-based optimization of reversible Toffoli circuits[J].Computer Science,2013,40(10):32-38(in Chinese).[程学云,管致锦,张海豹.基于规则的可逆Toffoli电路优化算法[J].计算机科学,2013,40(10):32-38.]

[11]FU Peng,SUN Quansen,JI Zexuan,et al.A method of SNR estimation and comparison IOR remote sensing images[J].Acta Ueodaetica et Cartographica Sinica,2013,42(4):559-567(in Chinese).[傅鹏,孙权森,纪则轩,等.一种遥感图像信噪比评估和度量准则[J].测绘学报,2013,42(4):559-567.]

[12]Khalaf W,Astorino A,D’Alessandro P.A DC optimization-based clustering technique for edge detection[J].Optimization Letters,2017,11(3):627-640.

[13]Shih M Y,Tseng D C.Wavelet-based multiresolution edge detection and tracking[J].Image and Vision Computing,2015,23(4):441-451.