采用改进RPCA的遥感影像去云算法

石晓旭，夏克文，王宝珠，常 虹，武盼盼

(河北工业大学 电子与信息工程学院，天津 300401)

0 引 言

如何在遥感影像中去除云层的遮挡，重构遮挡区地貌细节信息，是遥感应用领域一个待处理的重要问题。目前，在遥感领域，不少学者根据云层的厚度提出了多种去云算法：针对薄云去除，一般将遥感影像转换到频域处理，常见有同态滤波法和小波分解等方法，但会丢失某些高频细节信息，造成信息量损失，而且无法去除云区和无云区之间的突变云域和小片云。对于厚云覆盖区域，几乎难以获取任何地貌信息，只能利用多时相、多传感器遥感影像进行融合处理，但需要复杂的影像配准、校正技术，容易造成去云后影像出现畸变、灰度突变、纹理不连续等多种问题。由此可见，对成分复杂云区的联合去云技术的研究具有十分重要的意义。

近几年，采用压缩感知[1]的稀疏模型发展突飞猛进，引起众多学者的关注，在采样过程中利用观测矩阵稀疏化原有数据信号，去除冗余信息，使数据更加鲁棒，去除了野点和稀疏噪声对数据的影响。低秩矩阵恢复(low-rank matrix recovery，LRMR)[2]是压缩感知稀疏模型的二维矩阵形式扩展，将观测矩阵表述为低秩矩阵与稀疏矩阵之和，再通过将非凸优化问题转化为凸优化问题求解低秩矩阵。目前，LRMR主要由鲁棒主成分分析(RPCA)矩阵补全(MC)和低秩表示(LRR)等3类模型组成。

本文针对同一区域、不同时相遥感影中的稀疏云层遮挡，提出一种采用改进的RPCA去云算法，即对原有RPCA算法中l0范数采取一种新的分式函数逼近方式，同时引入加权核范数对奇异值阈值进行自适应的调节，满足保留数据主要成分的实际需要，使改进的RPCA算法在处理遥感影像去云问题时更为有效，实现复杂的稀疏云区的联合去云处理。

1 问题的提出

在鲁棒主成分分析(robust PCA，RPCA)模型中，观测矩阵D∈Rm×n往往具备低秩或近似低秩结构，但是同时存在较大的稀疏噪声干扰，如果将矩阵D表示为一个低秩矩阵和一个稀疏矩阵之和，则从中恢复出原有矩阵的低秩结构的概率较大，能够去除毁损矩阵结构的稀疏噪声。恢复低秩矩阵A可描述为如下双目标优化问题

(1)

通过引入折中因子λ(>0)，将低秩矩阵恢复的双目标优化问题式(1)转化为式(2)最小化问题

(2)

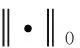
本文研究的多时相的遥感影像具有明显的时间相关性，即图像地物特征在一段时间内比较稳定，图像序列之间具有极大的相似性，所以由多幅地物像素组成的观测矩阵具有低秩特性；而处于动态变换状态中的云这一要素是非常不稳定的目标，不具备低秩性，同时，在图像上的分布范围比较小，在由多幅遥感影像组成的观测矩阵中分布更加稀疏，具有显著的稀疏特性。所以，在去除遥感影像中稀疏云层时，可以利用观测矩阵的低秩和稀疏两种特性，构建去云模型，实现低秩矩阵恢复。

针对遥感影像去云的RPCA算法模型可描述为：所观测的多时相遥感影像包含n个图像序列，每个图像像素值均可转化为一个m维列向量，那么便可构造m×n维观测矩阵D来表示输入遥感影像序列，待恢复的低秩矩阵A表示具有极大相似性的地物信息，稀疏矩阵E表示分布范围较小的云层部分，即D=A+E，于是形成式(2)所示的凸优化问题。通过有效的算法求解，恢复出A和E，就可以实现成分复杂的稀疏云区的联合去云。

2 改进的RPCA算法研究

本节主要针对式(2)中的稀疏矩阵E和低秩矩阵A进行改进，其中，为增加稀疏矩阵E恢复成功率，构建基于分式函数的RPCA模型；为增加低秩矩阵A的低秩性，采用加权核范数最小化算法(WNNM)中自适应阈值对奇异值进行相应地收缩。

2.1 基于分式函数的稀疏矩阵优化算法

2.1.1 模型改进

在式(2)中，由于低秩矩阵恢复优化模型的秩函数和l0范数都是矩阵空间上的非连续函数，因此难以得到式(2)的最优解，所以需要对其进行凸松弛处理。

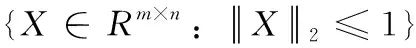
(3)

凸松弛为

(4)

而针对l0范数优化问题，现有的算法[3]主要有贪婪算法、迭代硬阈值算法、基追踪算法、迭代重赋权最小二乘极小化等算法，但是这些算法误差比较大，很难精确恢复稀疏解，并且在处理本文遥感影像序列这类大规模矩阵时，计算的复杂度会变大，计算速度也会相应的变慢。为了更好挖掘稀疏矩阵的稀疏度，增强恢复稀疏信号的能力，提高有噪音干扰的情况下算法的稳定性，本文考虑利用分式函数ρb(|t|)去替代不连续l0范数，分式函数图像如图1所示

(5)

式中：b∈(0,+∞)。

图1 分式函数图像

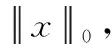
(6)

2.1.2 模型求解过程

为求解式(6)的优化问题，本文对式(6)构造相应地增广拉格朗日函数，如式(7)所示

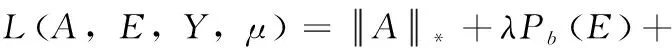
(7)

其中，Y∈Rm×n表示拉格朗日乘子，惩罚参数μ>0，·是标准内积，当Y=Yk，μ=μk，使用交替投影法[4]求解块优化问题交替迭代更新矩阵A和E，直到满足最优解收敛条件为止。

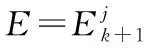
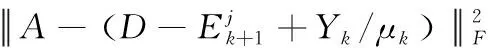
(8)

其中，奇异值算子Dε(Q)=USε(∑)VT，U∑VΤ为矩阵Q的奇异值分解，软阈值Sε(Q)的第(i,j)个元素为max(|qij|-ε,0)sgn(qij)，ε为大于0的常数。

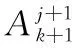
(9)

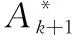
(10)

步骤4 更新参数μ

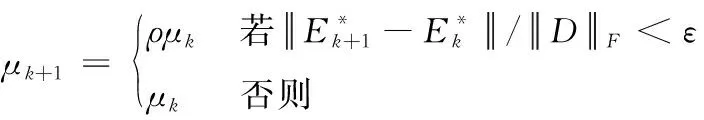
(11)

其中，ρ>1为常数；ε>0为比较小的正数。

不难发现式(9)仍是非凸优化问题，难以求解，为求解式(9)最优解，我们引入无约束DC规划问题，利用DCA算法[5]，将非凸优化问题转化为凸优化问题，快速求解大规模优化问题。

在DCA算法中，无约束DC规划问题如式(12)所示

minf(x)=g(x)-h(x)s.t.x∈RN

(12)

其中，g和h是RN上的下半连续凸函数。

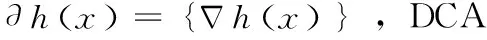
minf(x)=g(x)-h(x)⟺

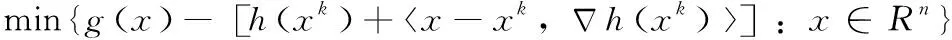
min{g(x)-x,vk:x∈Rn,vk∈∂h(xk)}

(13)

那么，对于式(9)的求解，可令

(14)

则

(15)

(16)

其实，迭代更新A和E时外层循环无需解出精确值，只需得到子问题的近似解就可以满足最优解的收敛条件，即低秩矩阵A和稀疏矩阵E的非精确更新公式为

Ak+1=argmin Γ(A,Ek+1,Yk,μk)=D1/μk(D-Ek+1+Yk/μk)

(17)

Ak+1+Yk/μk)

(18)

其中

(19)

2.2 采用WNNM的低秩矩阵优化算法

上文已经介绍了基于分式函数的RPCA算法的实现过程，不难发现，借助奇异值算子更新低秩矩阵时，使用了固定常数ε对阈值进行收缩，但是在实际应用中，大的奇异值表征数据的主要成分。为了提高矩阵的低秩性，本文对奇异值根据大小进行了不同收缩，赋予相应的收缩阈值，更符合实际情况，实现更好的恢复效果。

Candes等提出了一种重加权范数最小化的思想，提升了在稀疏恢复方面的效果。之后，Gu等提出了加权核范数最小化算法(weighted nuclear norm minimization，WNNM)[6]，其优化模型表示如下

(20)

(21)

式中：c为大于0的常数。σi(L)的初始值设为

(22)

因此，在本文改进RPCA算法中更新低秩矩阵A时，修改式(8)中的奇异值算子如式(23)所示

SW(∑)=max(∑ii-wi,0)

(23)

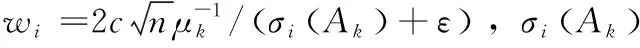
2.3 改进RPCA的整体算法

正如上两节所述，在本文改进的RPCA算法中，设计采用分式函数对l0范数逼近，结合DCA算法将非凸优化问题转化为凸优化问题求解，进一步提高稀疏矩阵恢复成功率，更适用于大规模遥感影像去云；同时引入WNNM算法中的权值向量对奇异值算子实现自适应收缩，增加地物矩阵低秩性，使算法具有更好的低秩矩阵恢复效果。改进RPCA的整体算法流程如图2所示。

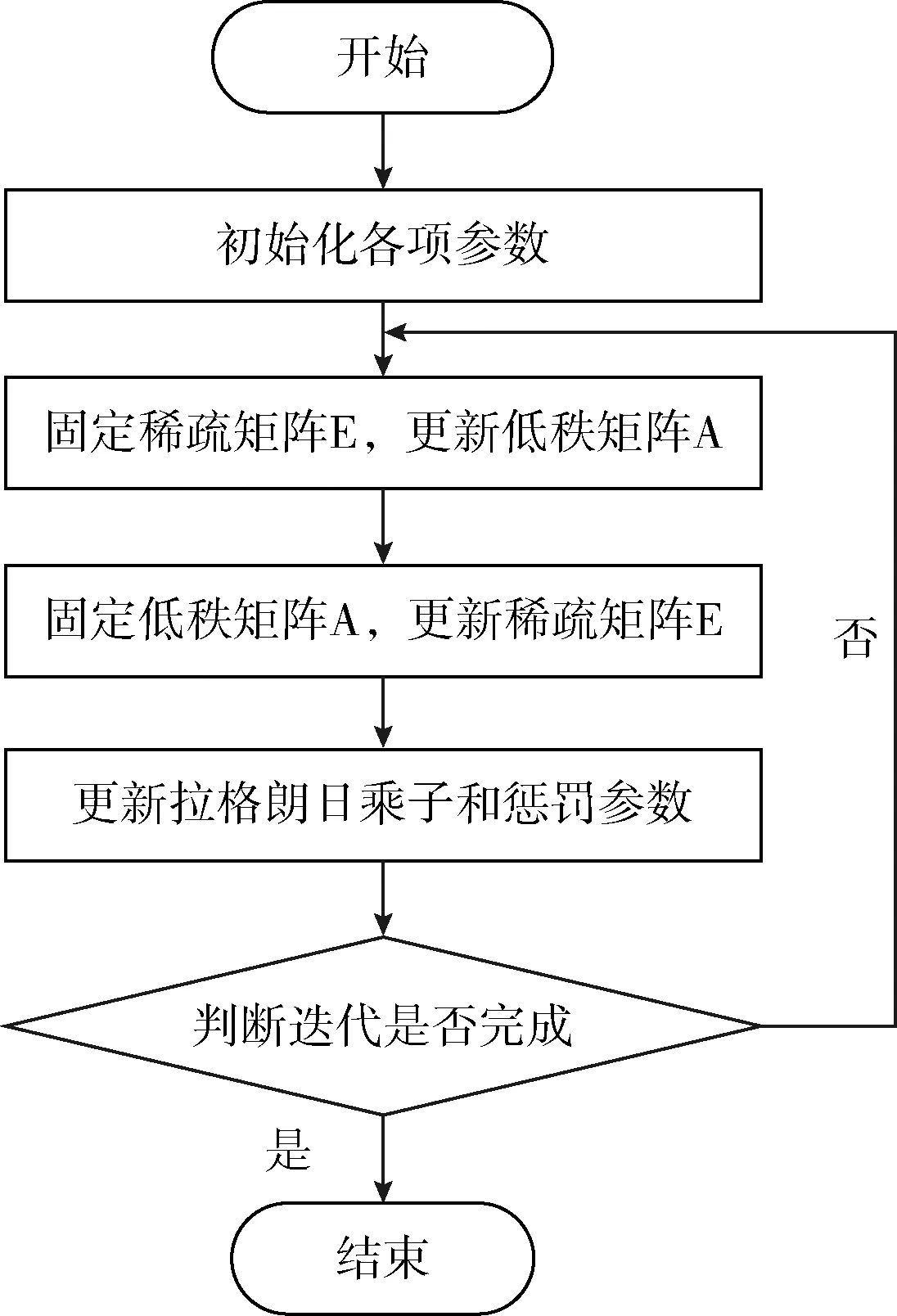
图2 改进RPCA的整体算法流程

改进的RPCA的整体算法如下所示：

步骤1 初始化Y0，A0=0，μ0，k=0，b=1.3

步骤2 while 不收敛 do

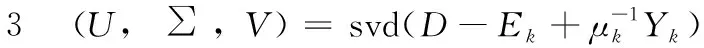
步骤4 更新权值向量W

步骤5SW(∑)=max(∑ii-wi,0)

基于此，本文选取东三省及西南地区部分省市A股上市公司2014～2015年数据为样本，实证检验影响企业研发支出资本化的相关因素。与以往研究相比，本文的主要贡献在于创新性地提出了系统风险这一因素对研发支出的影响，同时为了检验不同行业不同因素对资本化的影响程度，将企业行业类别分为高新技术企业和非高新技术企业，对比分析不同企业环境下研发支出资本化的不同结果，为客观观察企业会计行为提供了一定的理论及实践依据。

步骤6Ak+1=USW(∑)VT

步骤7

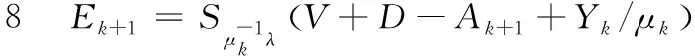
步骤9Yk+1=Yk+μk(D-Ak+1-Ek+1)

步骤10 更新μk

步骤11k=k+1

步骤12 end while

3 实验结果与分析

3.1 遥感影像去云算法设计

针对遥感影像云层遮挡区域的复杂情况，本文设计一种采用改进RPCA算法的遥感影像去云算法。

由于技术限制，获取同一区域的多幅遥感影像时，地理空间上会存在一定角度偏移。此外，由于光照、局部地理环境、拍摄时间等多种因素的干扰，会导致影像亮度不均。首先，基于精度和色彩一致性的要求，本文的改进RPCA去云算法对遥感图像序列做预处理，即采用SIFT算法的图像配准[7]以及Wallis匀色[8]。其次，针对云区，通过构造低秩观测矩阵，利用改进的RPCA算法去除；最后重构出无云遥感影像序列，实现了遥感影像复杂稀疏云区的联合去云处理。

具体去云算法流程如图3所示。

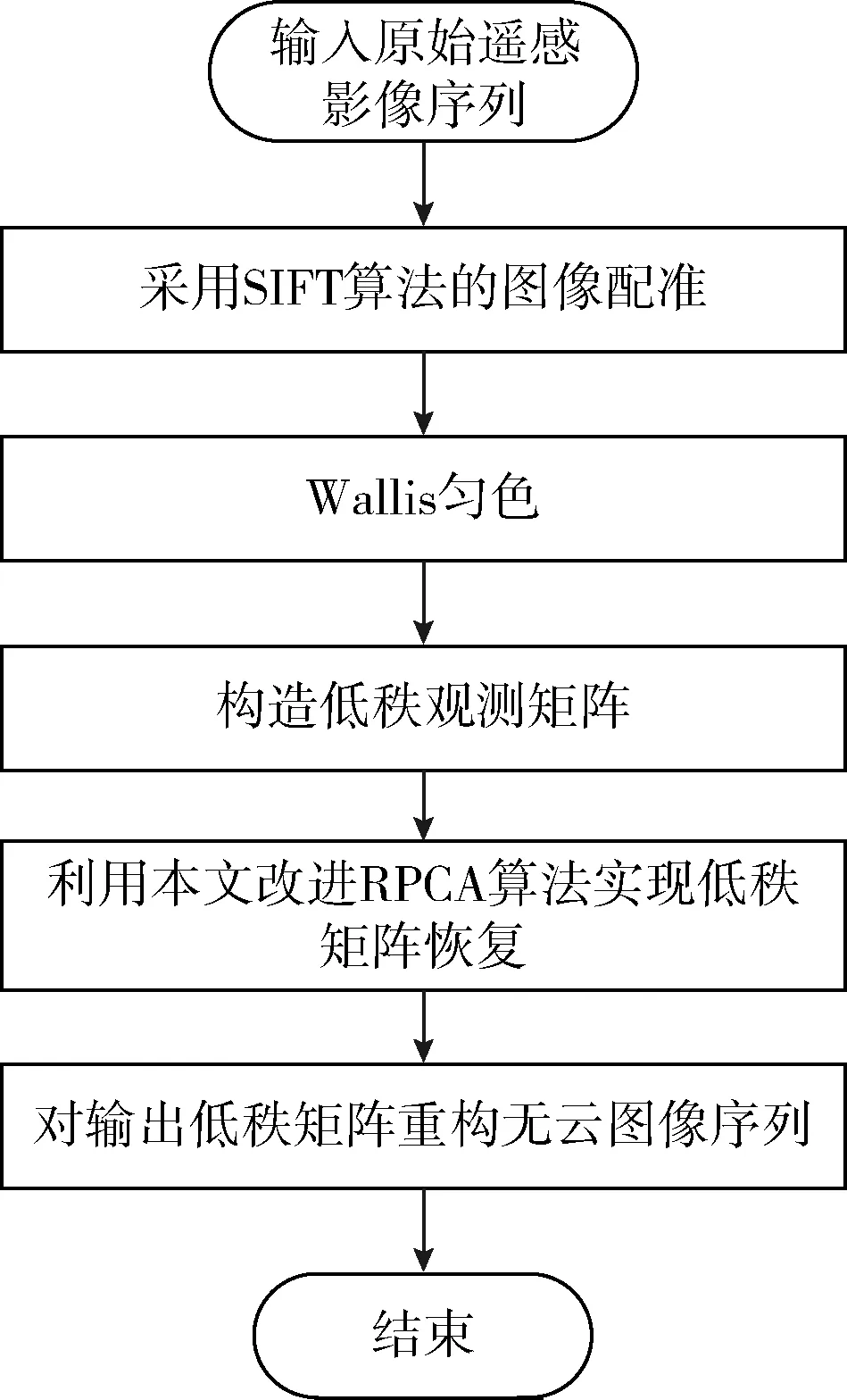
图3 采用改进RPCA的遥感影像去云算法流程

3.2 实验结果与分析

为了验证本文采用改进RPCA的去云算法在复杂稀疏云区的去云效果，本文采用LANDSAT 8卫星采集的一组不同时相的10张遥感影像数据作为实验原始影像进行去云处理实验，与传统去云算法(同态滤波法[9]、小波分解法[10])以及常见RPCA算法如APG[11]和IALM[12]进行对比实验，原始影像数据如图4所示。

本文实验环境为：Windows 8系统，Intel(R)Core(TM)i7-4720HQ CPU@2.60 GHz,8 GB内存的PC机器，算法采用MATLAB R2014b编程实现。

为比较复杂稀疏云区的去云效果，选取图4原始遥感影像中图4(c)和图4(j)两幅云特征鲜明的影像进行分析，去云结果如图5和图6所示。

图4 原始影像数据

图5 影像c去云结果对比

图6 影像j去云结果对比

从图5和图6中可以明显看出，同态滤波法和小波分解法对部分薄云区域有一定去除能力，但对小块云层无法有效去除；而RPCA算法(APG、IALM)及本文改进的RPCA算法对于稀疏云区(小片薄云、小片厚云、突变云区以及成分复杂的混合云区)，有非常明显的去除效果。其中，本文改进的RPCA算法处理结果图在云层去除、景物信息增强及清晰区域的保护方面的表现均优于APG算法和IALM算法。

为了定性评价遥感图像去云效果，我们采用图像灰度均值、标准差和熵这3项指标参数来分析。

(1)均值

(24)

图像均值表征图像平均灰度值，稀疏云区灰度值比较高，因此去云之后均值会下降。式(24)中f(x,y)表示大小为M×N的图像矩阵各像素点灰度值。

(2)标准差

(25)

标准差表示各像素点灰度值偏离均值的程度，去云之后遥感图像各像素点之间灰度值更加接近，标准差相应变小。

(3)熵

(26)

熵用来度量图像所含信息量的多少，在去云处理中，必须保证主要信息不丢失，所以熵也是一个很重要的的评价指标。式(26)中Pi表示第i级灰度值的出现概率。

根据上述3个指标，我们针对图5和图6，计算出具体指标参数值，分别见表1和表2。

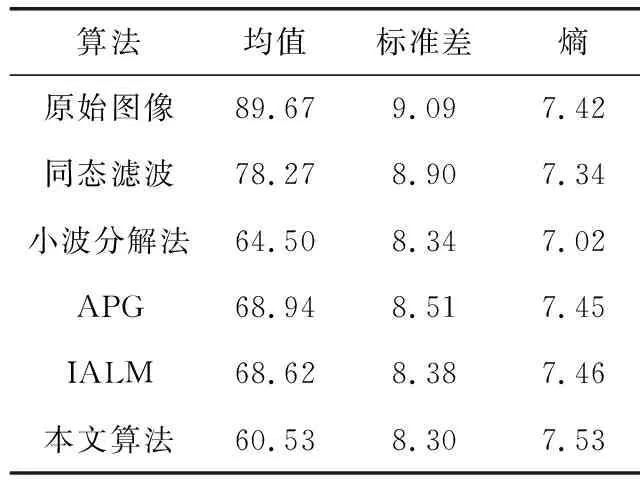
表1 影像c去云结果比较

表2 影像j去云结果比较

可以看出，采用本文算法对遥感影像处理后，图像灰度均值和标准差均有很大程度下降，说明去云效果明显，而且熵值略有增加，表明图像信息量得到了保护，图像更加清晰，符合预估。同时，在均值、标准差和熵3项指标上，本文改进的RPCA算法均占优势，处理后的图像具有最低的均值和标准差，同时熵值最大，弥补了传统算法易造成的信息量的丢失。

下面分析APG、IALM及本文改进的RPCA算法在运行时间、迭代次数的数据比较，见表3。

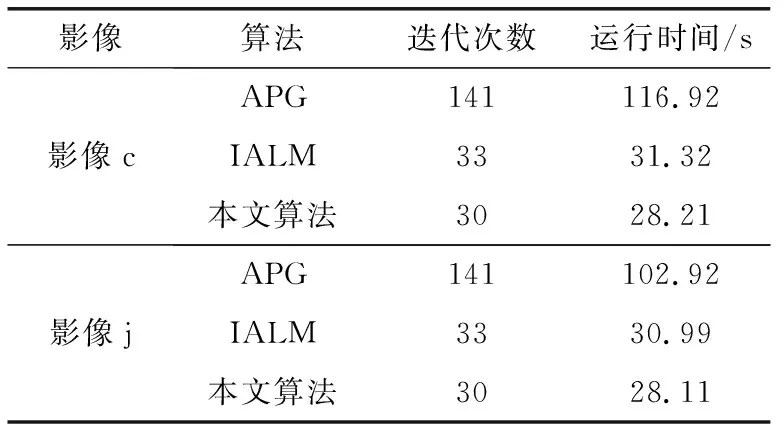
表3 RPCA算法性能比较

改进的RPCA算法运算速度更快，需要更少的迭代次数就可以实现收敛，具有更好的建模效果。综合实验结果表明，本文采用改进的RPCA遥感影像去云算法，在复杂的稀疏云区去云方面比传统去云算法有更好的表现；同时，在去云效果和运行时间方面，均优于常见RPCA算法，具有更好的实际应用价值。

4 结束语

本文利用RPCA算法模型来解决遥感影像复杂的稀疏云区的去云问题，将传统去云处理中需要解决的云层厚度问题转化为恢复遥感影像的低秩和稀疏成分；同时，对原有算法中l0范数采取一种基于分式函数的新的逼近方式，引入了加权核范数对奇异值阈值进行自适应的调节，提高稀疏成分恢复的成功率，增大低秩矩阵的低秩性，使改进算法更适用于大规模实际问题。

实验结果及其分析表明，本文提出的采用改进RPCA的遥感影像去云算法，能够有效解决稀疏云区(小片薄云、小片厚云、突变云区以及成分复杂的混合云区)的去云问题，同时还能保护图像的信息量，算法稳定，在主观视觉效果和客观评价标准方面优于其它方法，有效实现了遥感影像复杂稀疏云区的去云处理。

参考文献：

[1]LEI Lixia,ZHANG Yuejin,HUANG Dechang.Compressed sensing applications in medical image compression[J].Journal of Computer Engineering and Design,2014,35(11):3898-3902(in Chinese).[雷莉霞,张跃进,黄德昌.压缩感知在医学图像压缩中的应用[J].计算机工程与设计,2014,35(11):3898-3902.]

[2]Chen Y,Jalali A,Sanghavi S,et al.Low-rank matrix reco-very from errors and erasures[J].IEEE Transactions on Information Theory,2013,59(7):4324-4337.

[3]Qaisar S,Bilal R M,Iqbal W,et al.Compressive sensing:From theory to applications,a survey[J].Journal of Communications & Networks,2013,15(5):443-456.

[4]Deng W,Yin W.On the global and linear convergence of the generalized alternating direction method of multipliers[J].Journal of Scientific Computing,2016,66(3):889-916.

[5]Thi HAL,Le H M,Tao P D.Feature selection in machine lear-ning: An exact penalty approach using a difference of convex function algorithm[J].Machine Learning,2015,101(1):163-186.

[6]Gu S,Zhang L,Zuo W,et al.Weighted nuclear norm minimization with application to image denoising[C]//IEEE Conference on Computer Vision and Pattern Recognition.Columbus:IEEE,2014:2862-2869.

[7]Kupfer B,Netanyahu N S,Shimshoni I.An efficient sift-based mode-seeking algorithm for sub-pixel registration of remotely sensed images[J].IEEE Geoscience & Remote Sensing Letters,2015,12(2):379-383.

[8]ZHU Qiaoyun,DA Xing.Dodging method for multi-source remote sensing images based on wallis filter[J].Geomatics & Spatial Information Technology,2012,35(10):130-132(in Chinese).[朱巧云,答星.基于Wallis滤波器的异源遥感影像匀光方法[J].测绘与空间地理信息,2012,35(10):130-132.]

[9]Shen H,Li H,Qian Y,et al.An effective thin cloud removal procedure for visible remote sensing images[J].ISPRS Journal of Photogrammetry & Remote Sensing,2014,96(11):224-235.

[10]Wang X X,Jiang L S,Chen Y P,et al.Thin cloud removal from remote sensing images with adaptive thresholds of wavelet transforms[J].Journal of the University of Electronic Science & Technology of China,2013,42(3):390-393.

[11]Xue Q,Wang H,Cui Z,et al.Electrical capacitance tomography using an accelerated proximal gradient algorithm[J].Review of Scientific Instruments,2012,83(4):043704.

[12]Bhardwaj A,Raman S.Robust PCA-based solution to image composition using augmented Lagrange multiplier(ALM)[J].The Visual Computer,2016,32(5):591-600.