网络化软件系统故障传播分析与可靠性评估
薛利兴,左德承,张 展
(哈尔滨工业大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)
0 引 言
网络化软件(networked software)[1]是部署在Internet环境中的软件系统的抽象,通常由若干个部署在不同服务器上的、能够完成一项或几项功能并对外提供服务的独立模块(如:Web服务、各种网络信息资源等)组成,它们通过Internet网络进行通信交互、彼此协作共同完成一项复杂的工作。与传统基于构件的软件(component-based software)类似,网络化软件系统同样采用分治的思想将复杂任务划分给多个不同模块来完成;且网络中的每个模块都具有模块化、信息隐藏、可重用等特性,这些模块也称为网络化构件(networked component)。当前常见的云应用[2](cloud application)、面向服务体系结构[3](service-oriented architecture)、网构软件[4](Internetware)等均为网络化软件的具体实现方式。
与本地化软件系统不同,网络软件系统中的构件通过互联网进行相互调用和数据传输,过程比传统软件更为复杂难控。一方面,不稳定的Internet不仅给软件系统的可靠性带来一定的负面影响,构件部署在远端服务器之上难以获取运行状态也使交互行为变得更加复杂。另一方面,构建系统更多使用的是互联网上已有的网络构件,可能是由不同组织或个人开发的免费构件,也可能是付费使用的商业化构件,这些构件的质量参差不齐难以完全控制,失效后会向后续构件输出错误的数据,从而引发软件系统内的故障传播。
本文依据网络化软件系统交互方式的特点,定义了符合实际系统的失效模式;分析了构件执行过程及构件间的网络交互过程,并考虑故障传播建立系统可靠性模型,详细列出了建模和求解的步骤;最后结合一个案例验证了模型的准确性。
1 相关工作
Cheung[5]将软件系统的可靠性表示为各个独立模块的可靠性和使用剖面的函数,提出了一种基于马尔可夫链的软件可靠性建模方法。通过模型求解和敏感性分析,发现执行频率高的模块的可靠性对系统整体可靠性有重要意义。据我们所知,该模型是最早应用状态法对结构化软件可靠性建模的方法。Wang等[6]对不同软件结构进行可靠性建模,包括:串行顺序结构、并行结构、主备容错结构、调用-返回结构等。很多研究都是以Cheung和Wang等的工作为基础实施的,例如:Isa等[7]引入了任务和资源等因素对系统可靠性进行评估;Brosch等[8]考虑了外部服务、软件运行环境等因素对系统可靠性的影响;Zheng等[9]将Web服务的历史失效数据与用户进行关联分析,提取新用户的位置、查找相似的历史数据、预测各Web服务的失效率,再根据软件架构预测系统全局可靠性;Distefano等[10]则分析了SOA不同服务组合的可靠性。遗憾的是,这些工作都忽略了系统内的故障传播。
Cortellessa和Grassi[11]考虑了故障传播对系统的影响,认为构件中发生的错误不一定会导致系统的失效,其有可能在后续构件的执行过程中被屏蔽,只有当错误传播到系统接口时才导致系统失效。为此,他们提出了一种考虑错误传播的软件可靠性建模方法,但只考虑了单一的数据错误,与很多实际情况不符,而且Avizienis等[12]也强调多种失效模式应该得到重视。Filieri等[13]遵循了Avizienis的观点,提出了一种考虑多种失效模式和错误传播的构件软件可靠性分析方法,但其只在抽象层次上考虑不同的失效模式、不涉及任何具体的失效模式和具体的系统。Pham和Defago[14]从错误检测的角度将失效模式具体化,同时考虑了顺序结构、并发结构、主备容错结构的执行,对构件软件可靠性进行分析与预测。随后,Pham和Defago[15]又在后续工作中详细讨论了软件中多种容错结构的建模与可靠性分析。
现有的软件可靠性模型/分析方法更多关注的是本地化的构件软件,没有考虑网络化构件之间的基于网络的不稳定交互过程。此外,网络化构件多数部署在远端第三方服务器之上,我们很难像本地软件一样判断其运行状态,因此我们只能从外部观察其行为、对失效模式进行定义。本文从客观实际出发,定义了两种常见失效模式,并提出一种针对网络化软件的可靠性建模方法,不仅对构件执行过程和网络交互过程进行了建模,也考虑了系统内的故障传播问题。
2 网络化软件失效模式
一个构件的失效可以从多个不同角度进行定义,如:域(domain)、一致性(consistency)、可检测性(detectability)等,其中最常见的是域的角度。构件的输出由两部分组成:值域(content/value domain)和时域(timing domain)。理论上,根据构件输出结果的值域和时域正确与否,可以将失效划分为:值域错误引发的失效、时域错误引发的失效、值域和时域同时出错引发的失效[12],具体还可以再进行细分,如图1所示。
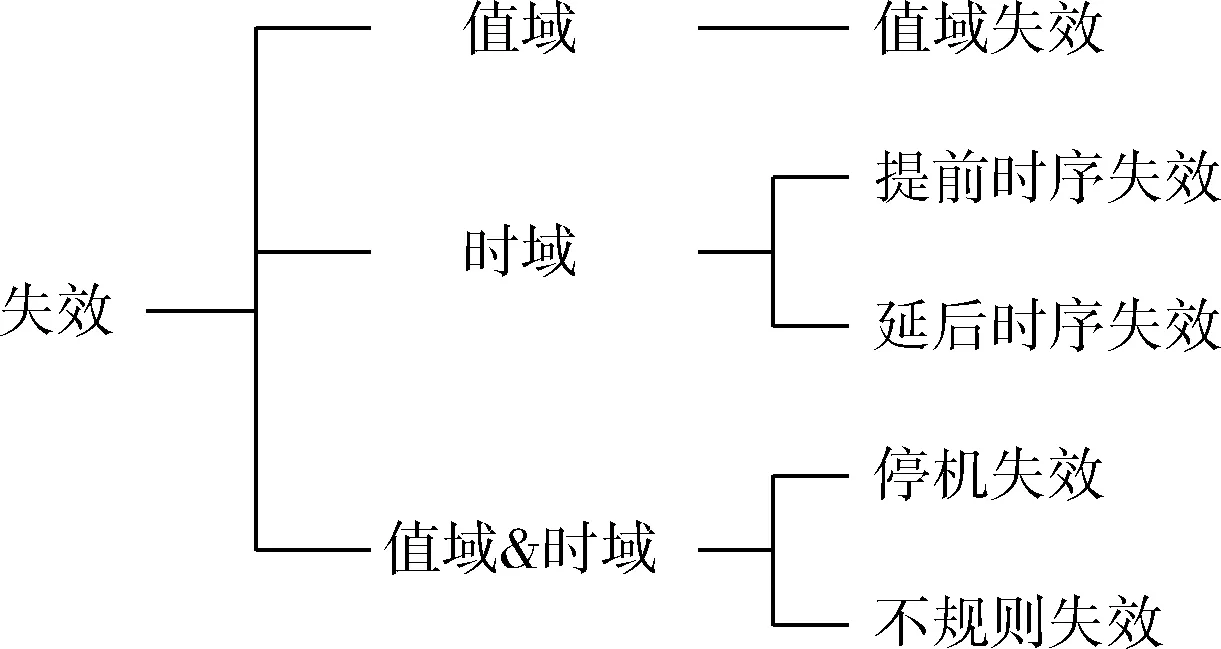
图1 理论中的失效模式分类
在多数的研究工作中,经典的失效分类应用并不多,特别是完全按照这个进行分类的几乎没有。主要因为多数系统对时域错误并不敏感,时域中的错误经常被忽略。通常情况下,只要系统在使用者可容忍的时间范围给出结果即可,人们更多关注失效的直观现象,如:停止运行(fail-stop)、停机(halt)等,有的甚至关注停止运行失效时是否给出相关信号。
在网络化软件系统中,构件多数运行在他人维护的服务器上,无论系统设计者还是用户都无法详细获知构件的运行状态,更多时候是通过等待时间的长短来判定构件是否失效。当构件没有在特定的时间内返回结果,即视其发生了失效,我们称之为超时失效(timeout failure)。若构件在指定的时间内给出了结果,则需要判断输出内容是否正确,进而得知是正确输出还是发生了值域失效(content failure)。
具体地,将这些失效模式的进行形式化定义。我们将网络化构件单次执行的结果定义为一个序对
其中,v是构件输出的内容,即值域结果;t为收到网络构件给出结果所需要的时间。
定义构件单次执行对应的设计输出为
其中,V是所有可接受的输出结果的集合,T*为构件正常执行所需的最长时间或用户可以等待的最长时间。
当构件的输出满足下列条件时视为正确输出,可以表示为
v∈V且t≤T*
当构件的执行时间超过规定时间,则视其发生了超时失效(timeout failure),形式化表示是
t>t*
若构件在规定的时间内给出结果,我们需要检查结果是否正确,若输出不满足设计规定的输出则视为值域失效(数据错误)
v∉V且t≤T*
事实上,很多系统中的系统失效都是通过时间长短来进行判断。例如:在嵌入式系统中,通常会采用看门狗(watchdog)技术判断系统是否失效。看门狗的本质为一个特殊计数器,当处理器没有在规定的时间内对计数器进行清0,则计数器会发生溢出引发相应的中断对系统进行重启。在大型主机系统或高可用集群系统中,多采用心跳检测(heartbeat detection)技术判断一个子系统或节点是否失效。心跳检测的本质与看门狗类似,系统需要在规定的时间发送特定的信号;否则,系统会被视为已经宕机或其中运行的关键服务已经发生失效。而在使用TCP协议进行网络传输过程中,若没有在指定的时间内收到对方的数据或接收确认,即视为本次传输失败,将重新发送数据。以上这几种情况都可以采用超时失效进行定义和描述。
为了更明确的、直观的展示正确输出(未失效)、值域失效、超时失效三者之间的关系,我们将它们在时间轴上进行表示,如图2所示。
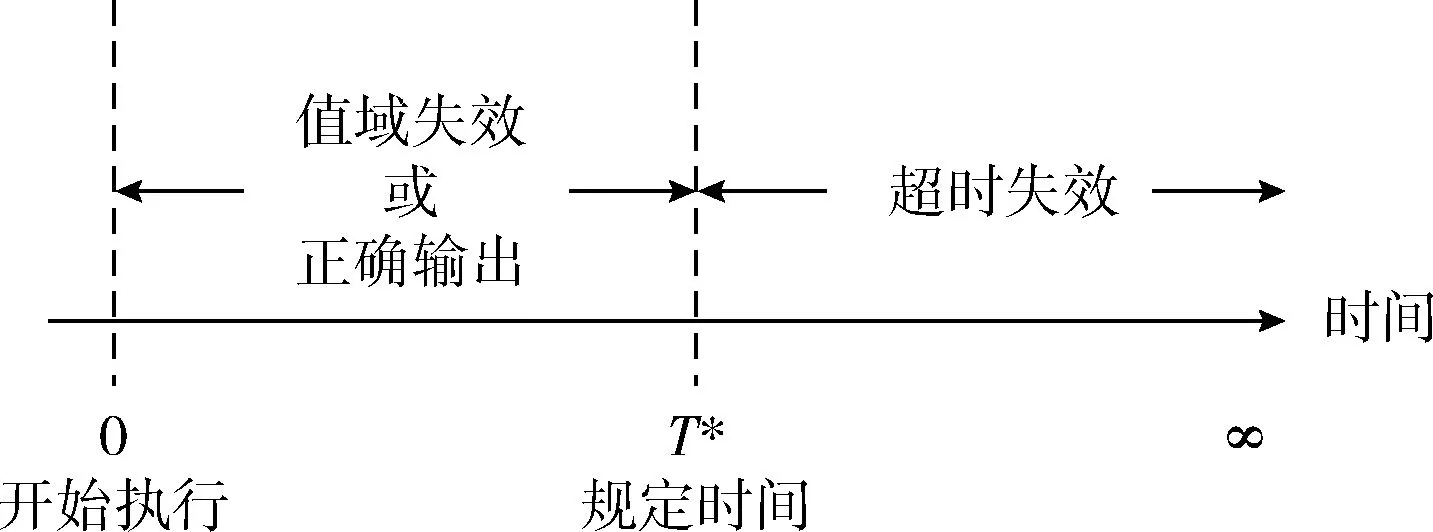
图2 构件的3种输出结果
3 故障传播与可靠性模型
在本节中,我们首先对构件执行过程和构件之间的网络交互过程分别进行分析和可靠性参数定义,之后利用马尔可夫链建立软件可靠性模型,并给出详细建模步骤和求解方法。
3.1 构件执行过程分析
与本地软件构件相同,网络化构件中一样会存在设计缺陷和编码错误,当它们被执行时便引发了构件内部错误,此时构件可能立即停止执行,也可能继续执行。在执行过程中,该错误有可能被屏蔽,只有当错误到达构件接口时才导致该构件失效。类似地,一个构件的失效也并非一定导致整个系统的失效,错误可能在其它构件中被屏蔽,只有错误传播到系统接口时才会引发系统失效。在构件的执行过程中,我们考虑以下5种故障传播情况:
第1种情况:在一个构件执行过程中,由于内部故障产生了错误,进而导致构件的执行时间超过规定时间的上限,即发生了超时失效,此时我们认为该构件无法完成其设计所规定的功能、无法给出执行结果。因此,该失效导致系统无法继续执行,直接导致系统失效。
第2种情况:构件在执行过程中,由于内部故障产生了错误,但构件在规定的时间内给出了结果,只是输出结果的内容不正确,此时发生了值域失效。尽管该构件失效,但系统依然继续执行,该错误输出被传播给后续构件。
第3种情况:当前续的构件产生错误输出(值域不正确)时,后面的构件不得不以错误的输入开始执行。在构件的执行过程中,错误可能被构件中的逻辑运算、比较运算等操作屏蔽,使得构件最终产生正确的输出结果。
第4种情况:构件接收错误的输入(值域不正确)开始执行,错误导致该构件在执行过程中导致死锁、死循环或崩溃等,导致该构件无法在规定的时间内输出结果,从而产生超时失效,并导致系统无法继续运行引发系统失效。
第5种情况:构件接收错误的输入(值域不正确)开始执行,但在执行过程中,错误既没有被屏蔽,也没有导致该构件执行超时,最终构件在规定的时间内输出了结果,但结果的内容依然不正确。
根据这几种情况,我们从正确输入和(值域)错误输入两个角度定义构件的可靠性参数,如图3所示。
正确输入:对于一个网络化构件Ci,在执行过程中由于多种原因可能在内部产生一个错误。该错误可能会引发死锁、死循环甚至程序崩溃,进而导致构件无法按时交付输出,产生超时失效,这种情况的概率记为tep(Ci);该错误也可能并不影响构件的运行时间,只影响构件的输出内容,这种情况的概率定义为cep(Ci)。此外,构件Ci也可能不输出任何错误,该情况的概率记为cop(Ci)。正确的输出包含两种情况,在内部发生错误但被屏蔽或者根本没有发生错误,但我们更关心输出情况,无需了解内部的细节。根据上面的定义,显然有:cop(Ci)+tep(Ci)+cep(Ci)=1。
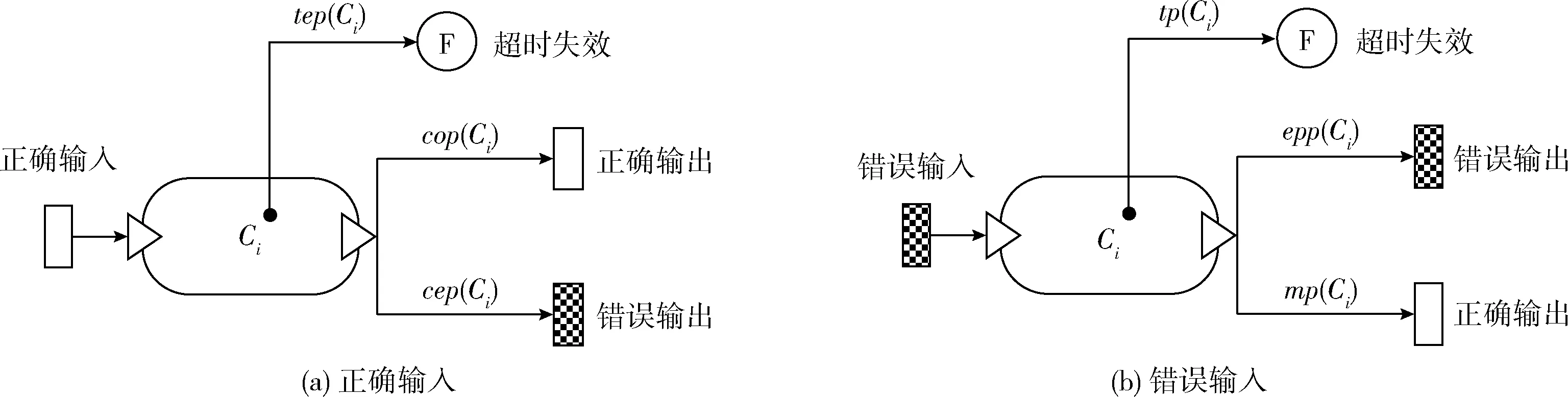
图3 构件的可靠性参数
(值域)错误输入:对于一个网络化构件Ci,接收值域错误的输入并在执行过程中将该错误屏蔽的概率记为mp(Ci);该错误也有可能引发该构件的超时失效,即发生失效转换,这种情况的概率定义为tp(Ci);此外,该错误可能没有被屏蔽也没有发生类型转换,而是从构件的输出接口传播出去,这种情况的概率记为epp(Ci)。显然有:mp(Ci)+tp(Ci)+epp(Ci)=1。
3.2 网络交互过程分析
与传统本地化软件不同,网络化软件中构件之间通过Internet连接进行数据传输,由于网络的不稳定性,在可靠性建模过程中我们必须考虑构件之间网络交互对整体的影响。
基于现有Internet协议架构,构件之间的数据传输可使用TCP协议或UDP协议。TCP协议本身能够保证数据可靠地、按顺序交付目标主机,当数据在传输过程中发生错误时,TCP协议自身会进行数据重传。而UDP协议是一种不可靠性的传输协议,通常系统设计者会增加一些相关机制来保证数据的正确传输。因此,综合TCP协议自身的机制和使用UDP协议的设计习惯,我们可以认为网络构件之间的数据传输中不会导致数据错误,但可能因为在规定的时间内未收到正确的数据而产生超时失效,从而导致整个软件系统的立即失效。
在网络化软件系统中,不仅构件是系统中的基本元素,构件之间的基于Internet的交互过程也是系统中的重要组成部分。在本文中,我们将构件之间的交互过程视为系统中特殊的构件,并进行可靠性参数定义,如图4所示。对于网络化构件Ci与Cj之间的交互过程Iij,在一次交互数据传输的过程中有两种情况:一种是数据在规定的时间内从构件Ci出发被Iij正确传输到达构件Cj,这种情况的概率记为cop(Iij);另一种情况是Iij没有在规定的时间内将构件Ci所输出的数据保持一致的交付给构件Cj,即在数据传输的过程中发生了超时失效,这种情况的概率定义为tep(Iij)。显然可知:cop(Iij)+tep(Iij)=1。

图4 构件间网络交互过程的可靠性参数
3.3 可靠性模型
一个软件系统的可靠性不仅依赖于每个构件的可靠性,还受这些构件的使用情况影响。构件使用情况通常用使用剖面(usage profile)来表示[5,6]。
假设系统中有n个构件,分别记为C1,C2…Cn,当构件Ci运行完毕后系统运行构件Cj的概率定义为Pij,所有这样的概率之集合{Pij}称为构件使用剖面。Pij可以根据系统的功能和设计进行预估,也可以在系统运行的过程中进行统计,具体计算方法为
其中,frqij是当构件Ci执行完毕后系统运行构件Cj的统计频率,如果构件Ci执行完毕后系统从未立刻运行过构件Cj,则有frqij=0,从而Pij=0;n为系统内网络化构件的数量。对于任意的构件Ci,有∑jPij=1。
我们利用马尔可夫链建立系统可靠性模型,假设系统从构件C1开始运行,在构件Cn运行结束后系统运行完毕,具体的建模步骤如下:
对于每个构件Ci,添加两个状态CC(i)和CE(i),分别表示构件接收正确输入和错误输入的执行过程;
对于每个网络交互过程Iij;添加两个状态IC(i,j)和IE(i,j),分别表示构件Ci产生正确输出和错误输出时数据从Ci传输到Cj的过程;
设置一个状态TE,表示因构件发生超时失效而引发的系统失效;
设置两个状态STARTC和STARTE,分别表示系统接收正确输入开始运行和接收错误输入开始运行;
设置两个状态ENDC和ENDE,分别表示系统结束运行时输出正确结果和系统结束运行时输出错误结果;
状态TE,ENDC和ENDE为吸收态,自转移概率为1;
从状态IC(i,j)到CC(j)的转移概率为cop(Iij),从状态IC(i,j)到TE的转移概率为tep(Iij);
从状态IE(i,j)到CE(j)的转移概率为cop(Iij),从状态IE(i,j)到TE的转移概率为tep(Iij);
从状态CC(i)到IC(i,j)的转移概率为Pijcop(Ci),从状态CC(i)到IE(i,j)的转移概率为Pijcep(Ci);从状态CE(i)到IE(i,j)的转移概率为Pijepp(Ci),从状态CE(i)到IC(i,j)的转移概率为Pijmp(Ci);
从状态CC(i)到TE的转移概率为tep(Ci),从状态CE(i)到TE的转移概率为tp(Ci);
从状态STARTC到CC(1)的转移概率为1,从状态STARTE到CE(1)的转移概率也为1;
从状态CC(n)到ENDC的转移概率为cop(Cn),从状态CC(n)到ENDE的转移概率为cep(Cn);
从状态CE(n)到ENDE的转移概率为epp(Cn),从状态CE(n)到ENDC的转移概率为mp(Cn);
从状态CC(n)到TE的转移概率为tep(Cn),从状态CE(n)到TE的转移概率为tp(Cn);
在这个马尔可夫模型中,系统从状态STARTC或STARTE开始运行,进入3个吸收态TE,ENDC,ENDE之一即运行结束。STARTC表示系统接收正确输入开始运行,STARTE表示系统接收错误输入开始运行,一旦进入状态TE表示某个构件或网络交互过程发生超时失效直接导致系统失效,进入状态ENDE表示有数据错误最终传播到系统接口,进入状态ENDC表示系统最终给出了正确的输出结果。
通常情况下,系统的可靠性定义为系统接收正确输入并给出正确输出结果的概率[13,14]。对应于我们的马尔可夫模型,系统可靠性等价于从状态STARTC出发到达状态ENDC的概率。
将马尔可夫模型对应的转移矩阵写成如下形式
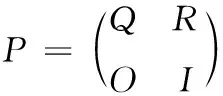
其中,子阵I为的3×3单位矩阵;子阵Q为方阵,且不包含与3个吸收态ENDC,ENDE和TE相关的转移概率;子阵R表示从其它状态到3个吸收态的一步转移概率,且R的3列从左到右分别表示ENDC,ENDE和TE。
设V=v(x,y)=(I-Q)-1R,从状态ENDC出发到STARTC的概率为v(1,1),因此系统的可靠性为R=v(1,1)
4 实验验证
本节通过一个案例来验证本文所提方法的正确性,并与现有方法进行对比。
如图5所示,系统中有5个网络化构件,表1和表2分别列出了构件接收正确输入和错误输入时的可靠性参数值,表3列出了各构件之间网络交互过程的可靠性参数。
根据软件系统的结构,建立对应的可靠性模型,将各构件的可靠性参数值、各网络交互过程的可靠性参数值以及使用剖面概率值带入模型之中,计算得到系统的可靠性为0.980 086。
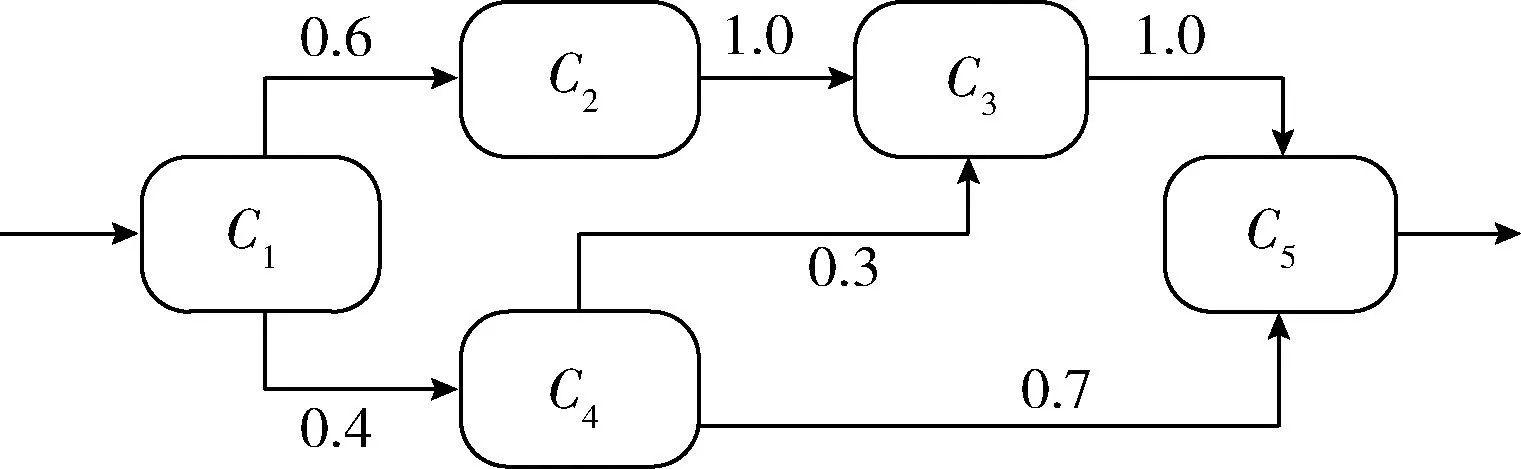
图5 实例系统的架构及构件的使用剖面
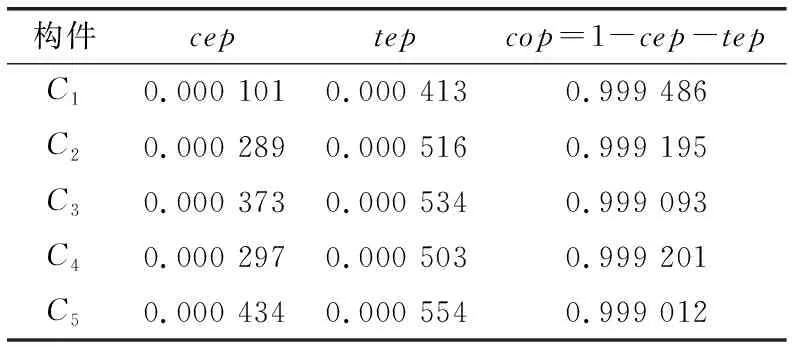
构件ceptepcop=1-cep-tepC10.000 1010.000 4130.999 486C20.000 2890.000 5160.999 195C30.000 3730.000 5340.999 093C40.000 2970.000 5030.999 201C50.000 4340.000 5540.999 012
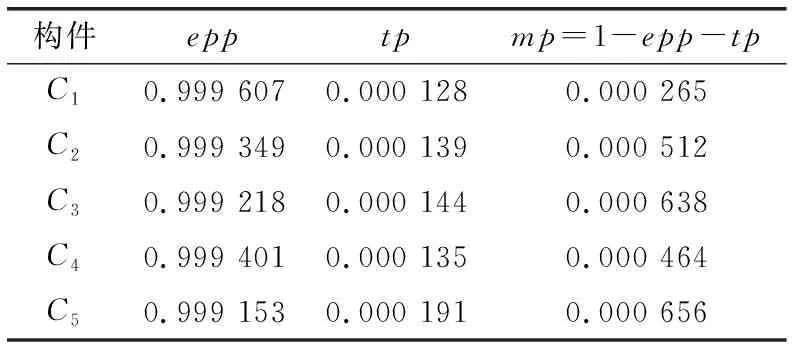
表2 构件接收错误输入时可靠性参数值
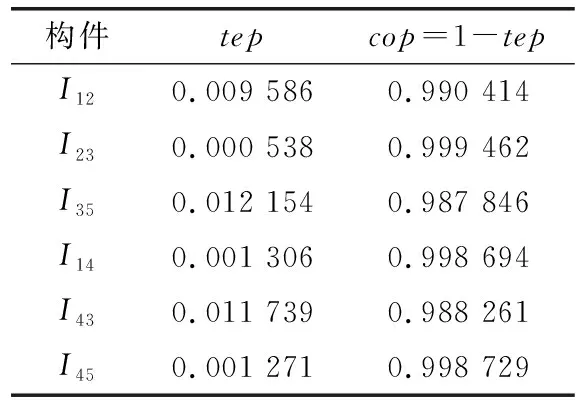
表3 网络交互过程的可靠性参数值
在实际系统中验证我们的模型是非常困难的,因为在软件系统中失效是小概率事件,可能需要花费相当长的时间才能观察到一次失效。为此,本文与现有的构件软件可靠性分析研究[7,8,14-16]一致,采用仿真实验来进行模型验证。对于目标系统中的每一个构件,实现一个名义(dummy)构件,即接口与原构件定义完全一致,但其内部只依据该构件可靠性参数定义的概率随机产生正确输出、错误输出及超时失效。对于构件间的各个交互过程,我们将其视为特殊构件,同样实现一个名义构件来模拟它们的工作过程。将各个名义构件按照目标系统架构和使用剖面进行组合连接,形成一个目标系统的仿真测试平台。在测试平台中,调用系统N次,观察系统输出,记录产生正确输出的次数NC,最终系统的可靠性为R=NC/N。
在本文的仿真实验中,共调用系统1 000 000次,即N=1 000 000,获得正确输出的次数为980 943,即Nc=980 943,因此系统的可靠性为0.980 943。本文模型计算得到系统的可靠性与仿真实验得到结果只相差0.000 857,误差率为0.874‰,可以认为本文模型足够接近仿真实验的结果。
Brosch等[16]提出的可靠性模型同样考虑了网络对软件系统的影响,应用该模型计算得到的系统可靠性为0.969 328,与仿真实验结果相差0.011 615,误差率为11.841‰,具体的对比结果见表4。此外,本文模型与Brosch模型的对比见表5。
Brosch模型将网络化软件划分为软件层和网络层,将系统整体可靠性视为它们二者可靠性的乘积;使用该方法的必须先得到网络层的可靠性,显然不适用于广域网或基于Internet的网络软件。本文将构件之间的各个网络交互过程视为相互独立的特殊构件,通过与使用剖面相结合建立离散时间马尔可夫模型,不仅符合广域网或Internet路由的特性,也可用于局域网内交互过程的抽象,适用范围更广。此外,Brosch模型中的可靠性参数没有给出明确定义,本文模型所用到的可靠性参数均来源于工程实践、给出了明确的定义,具有更强的可操作性和现实意义。

表4 仿真结果与模型计算的比较

表5 本文模型与Brosch模型的对比
5 结束语
本文针对网络化软件系统提出一种可靠性建模方法,不仅考查了各构件及构件间网络交互过程对系统的影响,也考虑了系统内的故障传播。首先,根据网络化构件的特点,提出了数据错误和超时失效两种符合工程实践的失效模式;经过对构件执行过程和网络交互过程的详细分析,从正确输入和值域错误输入两种情况定义构件可靠性参数、将构件执行过程及故障传播形式化,同时将网络交互过程视为系统内的特殊构件定义可靠性参数、将网络的影响形式化,最后利用马尔可夫链建立网络化软件可靠性模型。实验结果显示,本文模型的结果足够接近于仿真实验结果;与现有模型相比,该模型适用范围广,且具有更强的可操作性和实践意义。
参考文献:
[1]MA Yutao,HE Keqing,LI Bing,et al.Empirical study on the characteristics of complex networks in networked software[J].Journal of Software,2011,22(3):381-407(in Chinese).[马于涛,何克清,李兵,等.网络化软件的复杂网络特性实证[J].软件学报,2011,22(3):381-407.]
[2]Larus J.The cloud will change everything[C]//Proc of the 16th Int Conf on Architectural Support for Programming Languages and Operating Systems.New York:ACM,2011:1-2.
[3]Sward R,Boleng J.Service-oriented architecture (SOA) concepts and implementations[C]//Proc of the ACM Conf on High Integrity Language Technology.Boston:ACM,2012:11-12.
[4]Zhang J,Lei H.Research status and prospect of Internetware reliability[C]//Proc of the 4th Int Conf on Computer Science and Network Technology.Harbin:IEEE,2015:401-411.
[5]Cheung R.A user-oriented software reliability model[J].IEEE Trans on Software Engineering,1980,6(2):118-125.
[6]Wang W,Pan D,Chen M.Architecture-based software reliability modeling[J].Journal of Systems and Software,2006,79(1):132-146.
[7]Isa M,Jawawi D.A reliability estimation model using integrated tasks and resources[J].Journal of Theoretical and Applied Information Technology,2015,74(2):171-182.
[8]Brosch F,Koziolek H,Buhnova B,et al.Architecture-based reliability prediction with the palladio component model[J].IEEE Trans on Software Engineering,2012,38(6):1319-1339.
[9]Zheng Z,Ma H,Lyu M,et al.QoS-aware web service re-commendation by collaborative filtering[J].IEEE Trans on Services Computing,2011,4(2):140-152.
[10]Distefano S,Filieri A,Ghezzi C,et al.A compositional method for reliability analysis of workflows affected by multiple failure modes[C]//Proc of the 14th Int ACM SIGSOFT Symp on Component Based Software Engineering.Boulder:ACM,2011:149-158.
[11]Cortellessa V,Grassi V.A modeling approach to analyze the impact of error propagation on reliability of component-based systems[C]//Proc of the 10th Int Symp on Component-Based Software Engineering.Medford:Springer Verlag,2007:140-156.
[12]Avizienis A,Laprie J,Randell B,et al.Basic concepts and ta-xonomy of dependable and secure computing[J].IEEE Trans on Dependable and Secure Computing,2004,1(1):11-33.
[13]Filieri A,Ghezzi C,Grassi V,et al.Reliability analysis of component-based systems with multiple failure modes[C]//Proc of the 13th Int Symp on Component-Based Software Engineering.Prague:Springer Verlag,2011:1-20.
[14]Pham T,Defago X.Reliability prediction for component-based systems: Incorporating error propagation analysis and different execution models[C]//Proc of the 12th Int Conf on Quality Software.Xi’an:IEEE,2012:106-115.
[15]Pham T,Defago X.Reliability prediction for component-based software systems with architectural-level fault tolerance mechanisms[C]//Proc of the 8th Int Conf on Availability,Reliability and Security.Regensburg:IEEE,2013:11-20.
[16]Brosch F,Buhnova B,Koziolek H,et al.Reliability prediction for fault-tolerant software architectures[C]//Proc of the Joint ACM SIGSOFT Conf on Quality of Software Architectures & Int Symp on Architecting Critical Systems.Boulder:ACM,2011:75-84.

