约束处理技术及应用*
雍龙泉,拓守恒,史加荣
1.陕西理工大学 数学与计算机科学学院,陕西 汉中 723001
2.西安建筑科技大学 理学院,西安 710055
1 引言
约束优化问题(constrained optimization problem,COP)是工程应用领域经常出现的一类数学规划问题。目前求解约束优化问题的算法可分为两类:梯度型算法和启发式算法。梯度型算法要求所有函数可导,常见的梯度型算法有序列二次规划法、拉格朗日法、简约梯度法、投影梯度法等。梯度型算法需要设置较好的初值点并需要函数的梯度信息,因此对于不可微以及没有显式数学表达式的问题无能为力,且求得的多为局部最优解。启发式算法是一种模拟自然进化过程的全局优化方法,它借用了达尔文“物竞天择、适者生存”的生物进化观点,通过选择、交叉、变异等机制来提高个体的适应性,进而达到最优。常见的启发式算法有遗传算法、模拟退火算法、禁忌搜索算法等。与梯度型算法相比,启发式算法无需梯度信息,是一种基于群体的搜索技术(梯度型算法从一个点开始搜索,而启发式算法从一个群体即多个点开始搜索),且对所优化问题的特征不敏感,具有鲁棒性强,搜索效率高,不易陷入局部最优等特点,已成功应用于工程优化问题[1-7]。
求解约束优化问题的两个难点在于:约束的处理和算法的选取。本文给出约束优化问题一种约束处理技术,将不等式约束转化为等式约束,进而通过构造静态罚函数将原问题转化为无约束优化,采用全局和声搜索算法求解。
2 约束处理
考虑如下约束优化问题:

这里,x∈Rn为决策变量;f(x)为目标函数;hi(x)=0为等式约束条件,gj(x)≤0为不等式约束条件,且hi(x)、gj(x)均为Rn上的n元函数,i=1,2,…,m,j=1,2,…,l;xL和xU分别表示决策变量的下界和上界。
目前较为常见的是将约束优化问题转换为无约束优化问题,采用启发式算法进行求解。而启发式算法是一种无约束的搜索技术,缺乏明确的约束处理机制,这促使研究者开发不同的方法来处理约束条件。
约束处理常给算法带来一些额外的参数,这些参数选取不当的话会导致溢出或者不收敛。于是,设计具有较好性能的约束处理方法显得尤为重要。较为流行的约束处理技术是将等式约束条件hi(x)=0转换为不等式约束|hi(x)|-δ≤0来处理,利用约束违反程度函数构造罚函数达到最优。这里等式约束条件转换为不等式约束条件使得可行域的拓扑结构发生了变化,而且这种变化与δ的取值有关。为了减少转换给算法性能带来的影响,可以考虑动态调节δ。但是,如何有效地设置参数δ仍是一个值得研究的问题[8-9]。
鉴于上述原因,本文利用绝对值函数的性质给出一种约束处理方法:将不等式约束转化为等式约束,且无需增加任何参数。考虑绝对值函数ϕ(t)=|t|,当t≥ 0,|t|=t;当t≤ 0,|t|=-t。于是,不等式约束gj(x)≤ 0 等价于gj(x)+|gj(x)|=0,j=1,2,…,l。从而问题(1)就等价于:
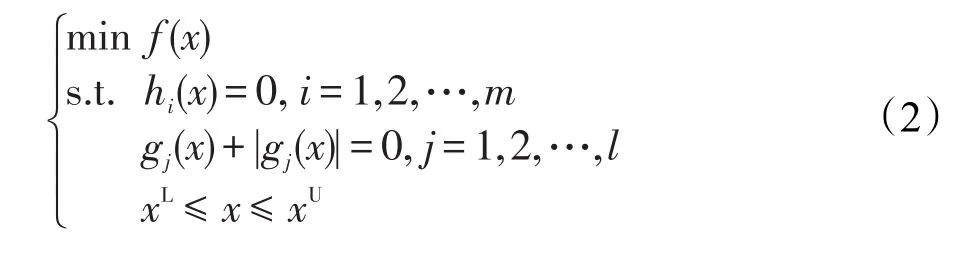
构造适应值函数:
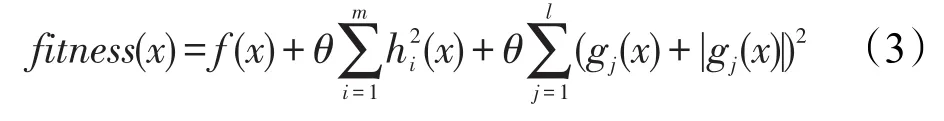
这里,θ是罚因子,如果θ随着迭代变动,则称式(3)为动态罚函数;若θ是一个常数(例如,取θ=105),则称式(3)为静态罚函数。式(3)是一个不可微的优化问题,下面采用启发式算法优化minfitness(x)。
3 优化算法
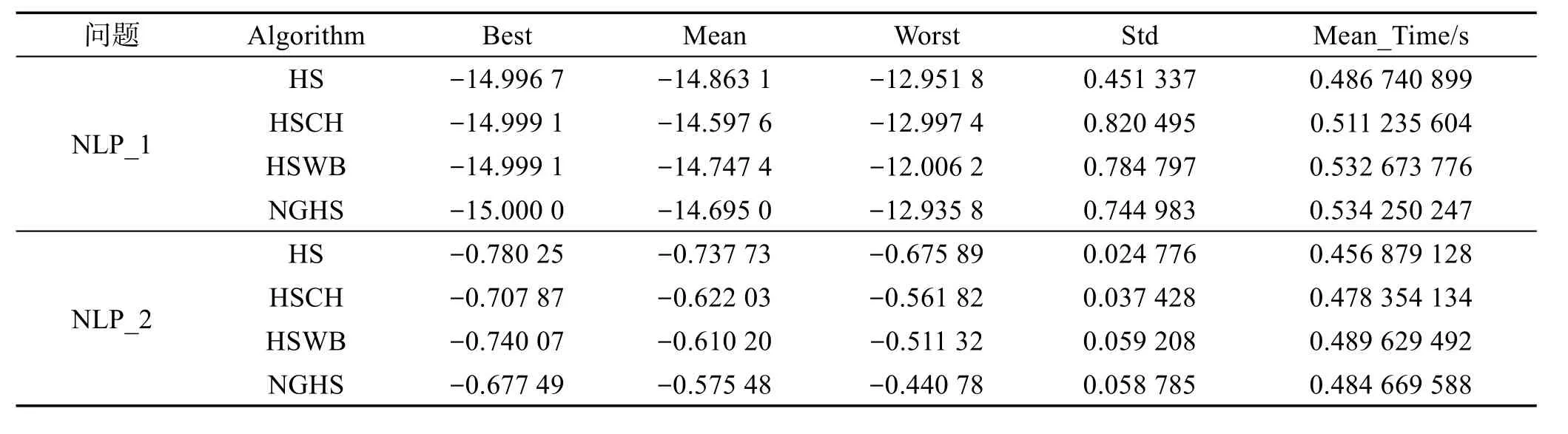
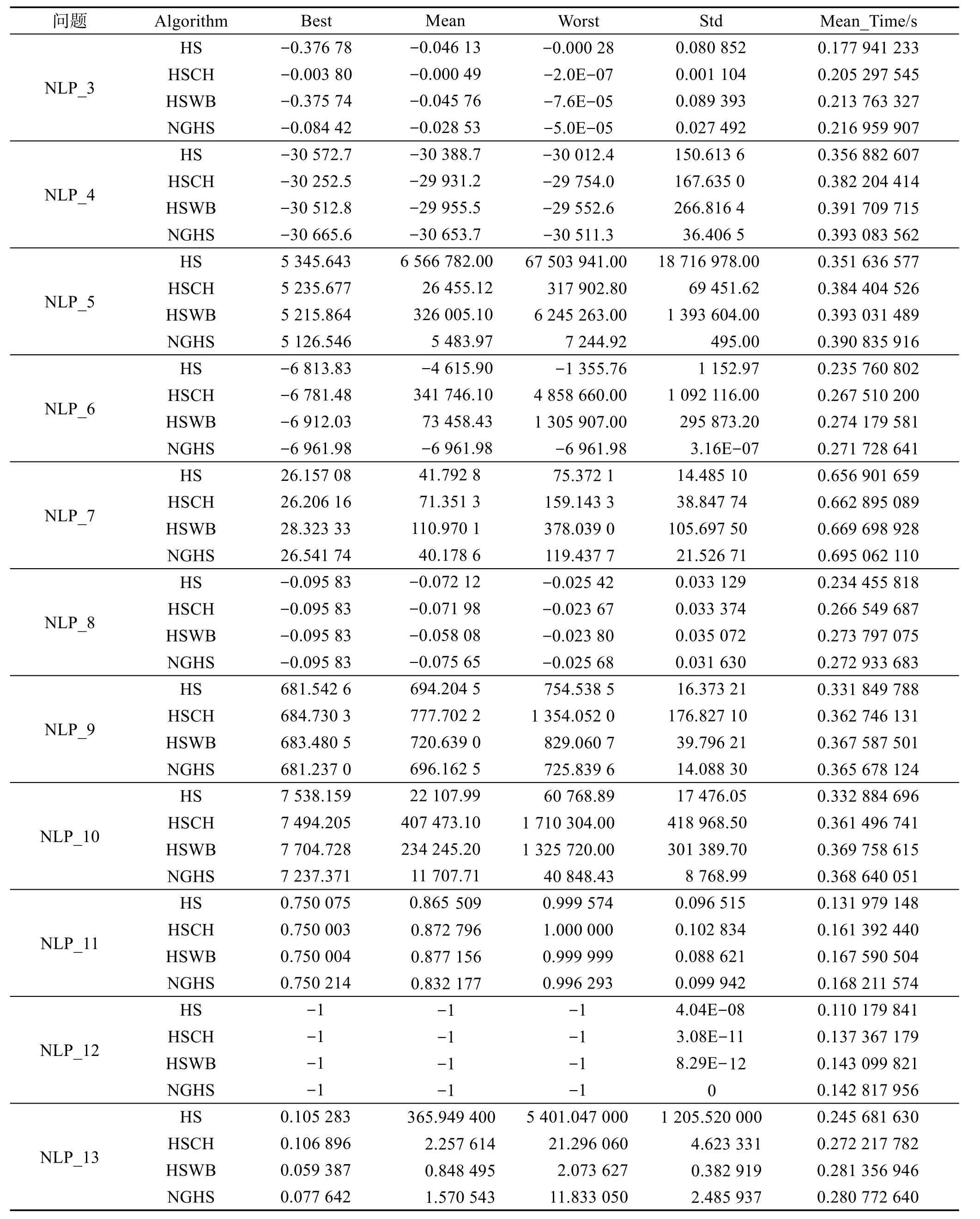
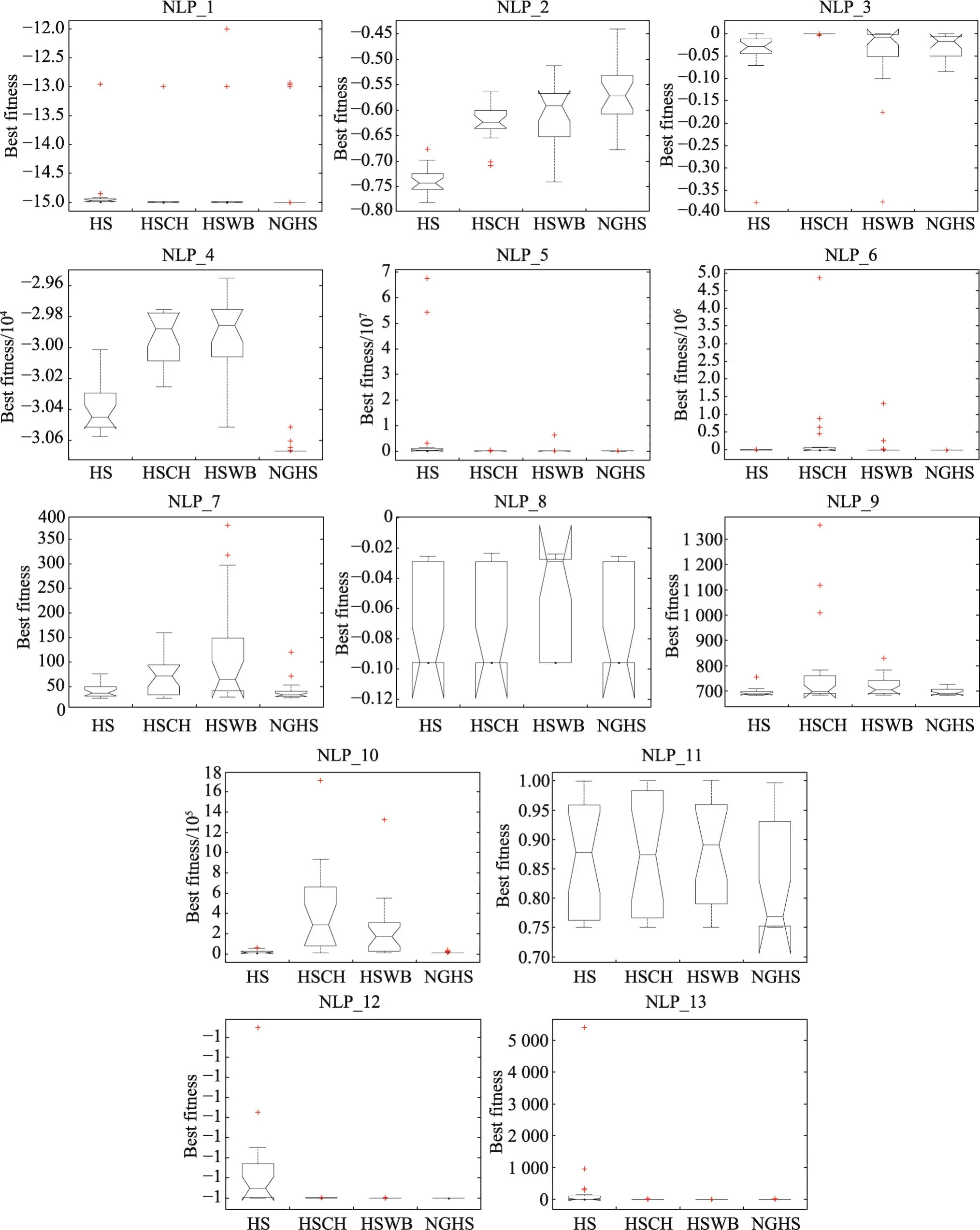
和声搜索(harmony search,HS)算法是Geem等人通过类比音乐和最优化问题的相似性而提出的一种现代启发式智能进化算法[10]。类似于遗传算法对生物进化的模仿,模拟退火算法对物理退火机制的模仿,以及粒子群优化算法对鸟群鱼群的模仿等,和声搜索模拟了音乐演奏的原理。和声搜索算法模拟了音乐创作中乐师们凭借自己的记忆,通过反复调整乐队中各乐器的音调,最终达到一个美妙的和声状态的过程。HS算法将乐器声调的和声类比于优化问题的解向量,评价即是对应的目标函数值。算法引入两个主要参数,即记忆库取值概率(harmony memory considering rate,HMCR)和微调概率(pitch adjusting rate,PAR)。算法首先产生 HMS(harmony memory size)个初始解(和声)放入和声记忆库(harmony memory,HM)内。然后,在和声记忆库内随机搜索新解,具体做法是:随机产生0~1的随机数rand,如果rand 经典和声搜索算法的基本步骤如下所示。 算法1HS算法 1.设置初始参数:决策变量个数N;各决策变量的搜索空间[XL,XU];和声记忆库的大小HMS;和声记忆的保留概率HMCR;音调调节概率PAR与调整步长bw;最大迭代次数Tmax。 2.在搜索空间内随机初始化和声记忆库HM,并计算每个和声向量的适应值。 3.利用和声库HM生成一个新的和声Xnew。 5.如果迭代次数达到Tmax,则结束并输出和声记忆库中最好和声向量,否则转至步骤3继续。 与其他智能算法一样,和声搜索算法也存在早熟现象。对和声搜索算法的改进主要集中在调节算法中的某些参数[12-15]。文献[13]采用位置更新和小概率变异策略,给出了一种全局和声搜索算法(novel global harmony search,NGHS),改进后的算法如下所示,其中Xbest和Xworst分别表示当前和声记忆库中最好和声与最差和声。 算法2NGHS算法 1.设置初始参数:决策变量个数N;各决策变量的搜索空间[XL,XU];和声记忆库的大小HMS;最大迭代次数Tmax;变异概率pm。 2.在搜索空间内随机初始化和声记忆库HM,并计算每个和声向量的适应值。 3.利用和声库HM生成一个新的和声Xnew。 NGHS与HS算法的区别见文献[16]。已有文献大多研究的是NGHS算法求解无约束优化,下面结合本文约束处理方法,采用NGHS算法求解约束优化问题。 为了测试约束处理及算法的有效性,选取13个带有约束的非线性规划标准测试问题(NLP_1~NLP_13)进行测试。这些测试问题是用进化算法很难取得全局最优解的一些具有代表性的函数,具体表达式见文献[17]。算法程序用MatlabR2009a编写,算法参数为HMS=15,HMCR=0.85,PAR=0.35,bw=(XU-XL)/1 000,算法终止的最大进化代数Tmax=20 000,在NGHS算法中选取pm=0.005,罚参数θ=105。为了便于观察NGHS算法的搜索性能,同时给出经典和声搜索算法(HS)、混沌和声搜索算法(harmony search algorithm with chaos,HSCH)[18]、最坏最好和声搜索算法(harmony search algorithm with worst and best strategy,HSWB)[19]的求解结果。为消除随机数对算法的影响,HS、HSCH、HSWB、NGHS算法各运行20次。表1给出了各算法运行20次后的最优适应值(Best)、平均适应值(Mean)、最差适应值(Worst)、标准差(Std)及运行时间(Mean_Time,取20次的平均值)。图1给出了每一个测试问题运行20次后的最优目标值的分布盒图。 由表1可看出:对于NLP_1、NLP_3、NLP_4、NLP_5、NLP_6、NLP_9、NLP_10,NGHS 优于 HS;对于NLP_2、NLP_7,HS优于NGHS;对于NLP_8和NLP_12,所有算法结果相当。对于NLP_11,HSCH结果稍优于其余算法;对于NLP_13,HSWB结果优于其余算法。这些结果表明,本文约束处理方法针对大部分测试函数是有效的,这也符合“No free lunch”原理[20]。下面给出一个具体的应用算例。 伸缩绳设计是典型的带有约束的工程优化问题,其数学描述如下: 取罚参数θ=108,求解伸缩绳设计问题的计算结果如表2所示(运行20次)。 NGHS算法最终求得的最优解为: Table 1 Statistical results for 20 runs表1 运行20次的统计结果 续表1 Fig.1 Boxplot of optimal solutions for 20 runs图1 运行20次后的最优目标值分布盒图 Table 2 Statistical results for 20 runs表2 运行20次的统计结果 由表2可知,本文算法求出的结果优于文献[21]中的结果,且计算结果稳定性好。 本文给出了一种约束处理方法,为各类工程优化问题约束处理提供了新的途径。下一步可以考虑采用本文约束处理方法,结合其他启发式算法求解可靠性优化[13]、结构优化[22-24]等工程问题。 : [1]Lin Dan,Li Minqiang,Kou Jisong.A GA-based method for solving constrained optimization problems[J].Journal of Software,2001,12(4):628-632. [2]Zhou Yuren,Li Yuanxiang,Wang Yong,et al.APareto strength evolutionary algorithm for constrained optimization[J].Journal of Software,2003,14(7):1243-1249. [3]Huang Haiyan,Gu Xingsheng,Liu Mandan.Research on cultural algorithm for solving nonlinear constrained optimization[J].ActaAutomatica Sinica,2007,33(10):1115-1120. [4]Huang Tianyun.Research advances on pattern searches in constrained optimization[J].Chinese Journal of Computers,2008,31(7):1200-1215. [5]Liu Ruochen,Jiao Licheng,Lei Qifeng,et al.New differential evolution constrained optimization algorithm[J].Journal of Xidian University:Natural Science,2011,38(1):47-53. [6]Saha C,Das S,Pal K,et al.A fuzzy rule-based penalty function approach for constrained evolutionary optimization[J].IEEE Transactions on Cybernetics,2014,46(12):2953-2965. [7]Mun S,Cho Y H.Modified harmony search optimization for constrained design problems[J].Expert Systems with Applications,2012,39(1):419-423. [8]Guo Guanqi,Wang Yong.Constraint-handling techniques based on evolutionary algorithms[J].Journal of Hunan Institute of Science and Technology:Natural Sciences,2006,19(4):15-18. [9]Wang Yong,Cai Zixing,Zhou Yuren,et al.Constrained optimization evolutionary algorithms[J].Journal of Software,2009,20(1):11-29. [10]Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:harmony search[J].Simulation,2001,76(2):60-68. [11]Yong Longquan.Advances in harmony search algorithm[J].Computer Systems&Applications,2011,20(7):244-248. [12]Mahdavi M,Fesanghary M,Damangir E.An improved harmony search algorithm for solving optimization problems[J].Applied Mathematics&Computation,2007,188(2):1567-1579. [13]Zou Dexuan,Gao Liqun,Wu Jianhua,et al.A novel global harmony search algorithm for reliability problems[J].Computers&Industrial Engineering,2010,58(2):307-316. [14]Siddique N,Adeli H.Harmony search algorithm and its variants[J].International Journal of Pattern Recognition andArtificial Intelligence,2015,29(8):1-22. [15]Wang Gaige,Gandomi A H,Zhao Xiangjun,et al.Hybridizing harmony search algorithm with cuckoo search for global numerical optimization[J].Soft Computing,2016,20(1):273-285. [16]Zou Dexuan.Heuristic algorithms and their applications in engineering optimization[D].Shenyang:Northeastern University,2011. [17]Runarsson T P,Yao Xin.Stochastic ranking for constrained evolutionary optimization[J].IEEE Transactions on Evolutionary Computation,2000,4(3):284-294. [18]Yong Longquan,Liu Sanyang,Tuo Shouheng,et al.Improved harmony search algorithm with chaos for absolute value equation[J].Telecommunication Computing Electronics and Control,2013,11(4):835-844. [19]Yong Longquan,Liu Sanyang,Tuo Shouheng,et al.Improved harmony search algorithm for absolute value equation[J].Journal of Natural Science of Heilongjiang University,2013,30(3):321-327. [20]Wolpert D H,Macready W G.No free lunch theorems for optimization[J].IEEE Transactions on Evolutionary Computation,1997,1(1):67-82. [21]Wang Ling,Qian Bin.Hybrid differential evolution and scheduling algorithm[M].Beijing:Tsinghua University press,2012. [22]Zou D,Liu H,Gao L,et al.A novel modified differential evolution algorithm for constrained optimization problems[J].Computers&Mathematics with Applications,2011,61(6):1608-1623. [23]Gandomi A H,Yang Xinshe.Benchmark problems in structural optimization[M]//Computational Optimization,Methods andAlgorithms.Berlin,Heidelberg:Springer,2011:259-281. [24]Gandomi A H,Yang Xinshe,Alavi A H.Cuckoo search algorithm:a metaheuristic approach to solve structural optimization problems[J].Engineering with Computers,2013,29(1):17-35. 附中文参考文献: [1]林丹,李敏强,寇纪凇.基于遗传算法求解约束优化问题的一种算法[J].软件学报,2001,12(4):628-632. [2]周育人,李元香,王勇,等.Pareto强度值演化算法求解约束优化问题[J].软件学报,2003,14(7):1243-1249. [3]黄海燕,顾幸生,刘漫丹.求解约束优化问题的文化算法研究[J].自动化学报,2007,33(10):1115-1120. [4]黄天云.约束优化模式搜索法研究进展[J].计算机学报,2008,31(7):1200-1215. [5]刘若辰,焦李成,雷七峰,等.一种新的差分进化约束优化算法[J].西安电子科技大学学报:自然科学版,2011,38(1):47-53. [8]郭观七,王勇.基于进化算法的约束处理技术[J].湖南理工学院学报,2006,19(4):15-18. [9]王勇,蔡自兴,周育人,等.约束优化进化算法[J].软件学报,2009,20(1):11-29. [11]雍龙泉.和声搜索算法研究进展[J].计算机系统应用,2011,20(7):244-248. [16]邹德旋.启发式算法及其在工程优化中的应用[D].沈阳:东北大学,2011. [19]雍龙泉,刘三阳,拓守恒,等.改进的和声搜索算法求绝对值方程[J].黑龙江大学自然科学学报,2013,30(3):321-327. [21]王凌,钱斌.混合差分进化与调度算法[M].北京:清华大学出版社,2012.3.1 经典的和声搜索算法

3.2 改进的和声搜索算法


4 约束优化数值实验结果
5 应用于工程优化问题
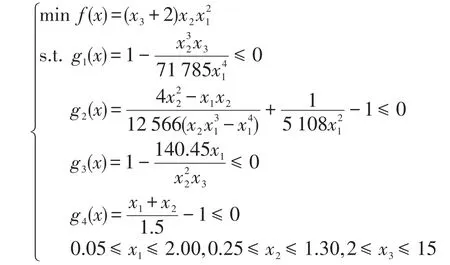



6 结束语

