基于程序特征的线程划分方法的研究*

马巧梅

宝鸡文理学院 计算机学院，陕西 宝鸡 721016

1 引言

按照摩尔定律[1-2]，半导体的发展已经从单核时代转变为多核时代，如何加速串行程序，从而充分合理地利用丰富的核资源成为一个研究目标。线程级推测（thread-level speculation，TLS）[3-4]能够自动将串行程序以激进的方式划分为多个线程，并允许线程间存在模糊控制依赖和数据依赖，多个线程在一个CMP（chip multiprocessor）上同时执行，从而挖掘程序的线程级并行性。各种新的线程级推测方案应运而生，典型的方案包含Stanford大学研发的Hydra[5]、Wisconsin大学研发的Multiscalar[6]、UIUC研发的线程级推测系统POSH[7]、国防科技大学开发的SMA（speculative multi-threading architecture）系统[8]、卡耐基梅隆大学的STAMPede[9]、Intel Barcelona研究院提出的Mitosis[10-11]、日本NEC公司的推测多线程系统Pinot[12]以及 Prophet[13-15]等。

线程划分方法对程序加速比提升至关重要。传统的线程划分多采用启发式规则进行。文献[16]在综合考虑线程划分的各种开销情况下使用一系列平衡最小割来划分程序，且在每次分割之后调整程序控制流图边的权重。文献[17]在给定计算架构情况下定量比较不同的划分算法，提出了一个新的动态划分算法Mex-slicing，虽然该算法整体性能超过其他动态划分算法，但在可预测性和代价方面难以达到平衡。然而，上述这些根据人工经验知识得来的启发式规则具有很大的局限性，且在指导线程划分中往往对所用待划分程序使用一套启发式规则，导致单纯地依靠启发式规则进行线程划分，很难得到最优线程划分结果，而只能得到经验上较优的线程划分结果。

为解决传统启发式规则在TLS中存在的不足，机器学习方法被成功引入到TLS中。文献[18]提出一个可移动编译器利用机器学习方法匹配程序的并行性到多核处理器的方法，并开发了两个预测器，一个数据敏感的和一个数据不敏感的来为并行程序选择最好的匹配。文献[19]开发了一个为数据并行应用在出现额外负载情况下预测最优线程数据的方法，并且开发了一个综合模型来减小额外负载的影响，提升平均加速比。文献[20]提出一个基于学习的方法以代价敏感的方式分配并行的负载到计算平台，该方法在决定负载分配之前用静态程序特征来聚类程序。上述机器学习在TLS中的应用主要集中在匹配、预测、负载分配等方面，而很少用于线程划分。

本文提出利用机器学习方法从TLS样本集中学习线程划分知识，并根据新程序的特征预测其划分方案，与传统基于启发式规则的线程划分进行了对比，探讨了本文方法在线程划分方面的优势。

2 执行模型和启发点

2.1 TLS执行模型

TLS实现将串行程序并行化，并在多核平台上并行执行，从而提高加速比性能。图1给出了TLS执行模型[21-22]，在该模型中线程激发点（spawning point，sp）和准控制无关点（control quasi-independent point，cqip）指令把串行程序映射成多线程程序。依据串行语义，在每一时刻只有一个线程允许提交数据到内存，这个线程被称作确定线程，而其他线程称作推测线程（speculative thread）。各个推测线程由两部分组成，即预计算片段（precomputation-slice，p-slice）和串行程序代码。p-slice是一小段代码，该代码是由编译器依据切片技术生成的，来预测推测线程中使用的live-ins（在定值之前还要被引用的变量集）。图1显示了SpMT执行的4种情况。在图1（a）中，推测多线程程序因为忽略sp-cqip，所以等同串行执行程序。在图1（b）中显示的是推测执行成功的情况：当确定线程T1执行到sp时，如果存在闲置的核资源，新推测线程T2被激发；否则，T2不被激发。当T1执行到cqip，将验证T2在p-slice中使用的live-ins。如果验证正确，则T1提交执行结果，并释放核资源。然后，确定执行的权限从T1传递给T1直接后继线程。图1（c）给出T2验证失败，推测执行失败，从而撤销T2，预计算片段不被执行的情况。图1（d）给出了出现读后写（read after write，RAW）依赖违规时，在当前状态下重新启动该线程的情况。

Fig.1 TLS execution model图1 TLS执行模型

2.2 启发点

图2显示了Olden基准程序集[23]中health（）过程同一子过程13个划分方案和过程加速比对应图。横坐标代表同一子过程的13种划分方案，纵坐标代表对应的加速比。划分方案用一个五维向量表示，该向量的组成将在第4章给出。图2给出的启发就是：过程的划分方案影响着过程划分后获得的加速比。如何根据程序特征预测其划分方案成为本文的一个研究目的。

Fig.2 13 partition schemes and speedups of procedures in health()图2 health（）中13个过程划分方案与过程加速比

3 划分方法框架

将一个串行的程序划分成为一个能够并行执行的多线程程序时，首先要提取程序特征，根据其特征获取较优的划分方案，然后根据划分方案进行线程划分。

图3给出了基于程序特征的线程划分框架图。其中，虚线框显示了KNN（K-nearest neighbor）算法从训练样本中学习线程划分知识，从而构建预测模型的过程。预测模型构建完成，通过待划分程序的特征作为模型的输入，预测出该程序的划分方案，并在Prophet系统[14-15]中指导其划分，生成多线程程序。然后在模拟器上完成评测，输出程序结果和加速比值。

Fig.3 Scheme of thread partitioning based on program characteristics图3 基于程序特征的线程划分框架图

该框架由5个主要部分构成，分别是：

（1）程序特征的表达；

（2）划分方案的表达；

（3）预测模型的构建；

（4）线程划分过程；

（5）实验评测。

下面将在划分方案中分别描述5个组成部分。

4 划分方案

4.1 程序特征的表达

基于程序特征的线程划分方法需要由Prophet系统的profiler统计程序运行时的信息，从而获取其特征信息。如果指令是分支指令，则根据跳转是否为循环回跳分别进行处理，若是常规跳转，将本次跳转情况更新。若是回边跳转，则由当前跳转跨越的动态指令数M与历史记录中的平均动态指令数LD-1以及总迭代次数D计算循环平均动态指令数LD；其次，如果该指令是过程返回指令，则由当前函数本次调用的动态指令数S与历史记录中的平均动态指令数NC-1，以及总调用次数C计算平均动态指令数NC；最后，profiler将结果注释在该函数的profile信息探针函数对应的信息域。

图4显示了profiler提取的特征初始存储结构。其中，c是动态指令数，l是循环分支概率，b是分支概率，d1是分支指令个数，d2是跳转指令个数，d3是加法/减法指令个数，d4是乘法/除法指令个数，n是程序基本块个数。矩阵M中每一个元素是一个特征向量，该向量包括动态指令数、循环分支概率、分支概率、分支指令个数、跳转指令个数、加法/减法指令个数、乘法/除法指令个数和程序基本块个数。

Fig.4 Expression of program characteristics图4 程序特征表示

本文采用静态和动态特征来代表输入样本程序，为了方便计算欧氏距离，选用x1~x8这8个变量来分别代表样本程序的特征，具体使用的特征变量以及它们的描述在表1中给出。

Table 1 Used characteristics and their descriptions表1 使用的特征和特征描述

4.2 划分方案的表达

划分方案的提取过程采用现有Prophet线程划分[24]中非循环划分和循环划分算法提取。划分算法（非循环划分、循环划分）的执行流程可以用图5中流程简图进行描述。从图5中可以看出，线程粒度的上限（upper limit of thread granularity，ULoTG）、线程粒度的下限（lower limit of thread granularity，LLoTG）、依赖数（data dependence count，DDC）、激发距离的上限（upper limit of spawning distance，ULoSD）、激发距离的下限（lower limit of spawning distance，LLoSD）直接影响着线程划分的过程，其中决策1和决策2是指不同的划分决策（比如激发新线程、循环展开、重新划分等）。如果线程划分过程中对新线程的划分可以归结为一个决策问题，那么这5个阈值是决定该问题答案的直接因素。可以得出一个结论：5个阈值的变化直接影响着划分的决策，从而影响着划分的结果。因此基于此本文选定这5个阈值作为优化的参数。

Fig.5 Flow chart of extracting partition schemes图5 提取划分方案的流程图

划分方案用H==表达。其中，LLoTG、ULoTG、DDC、LLoSD、ULoSD是线程划分过程中影响划分效果的5个主要参数。

4.3 预测模型的构建

预测划分方案的流程一般是首先获取线程级推测的样本集，然后当一个新的程序将要划分时，首先提取程序中各个过程的特征，然后运用KNN方法从样本集预测将要划分程序的划分方案。

样本集可以形式化表示为T={Xorig-i,Hpar-i}(i∈1,2,…,N)，在样本集中，每个训练样本都是由程序过程的特征向量Xorig和它所对应的近似最佳划分方案Hpar组成。每个特征向量Xorig=[x1,x2,…,xn]对应于N维空间中的一个点，每个近似最优的划分结构Hpar也是由一组参数组成，即Hpar=[h1,h2,h3,h4,h5]，其中h1表示线程粒度的下限，h2表示线程粒度的上限，h3表示数据依赖数，h4表示激发距离的下限，h5表示激发距离的上限。

当两个过程具有相同的特征，那么这两个过程就要有相同的划分方案，这是预测划分方案的前提条件。基于KNN的划分方案的预测，首先需要构建预测模型，所有的训练样本都存储在训练样本中，构成了一个KNN预测模型。基于KNN的分类方法只是简单地把所有的训练样本存储起来，样本的分类延迟到一个新的样本需要分类的时候。当一个新的程序需要划分时，首先提取程序的特征，然后找到距离它最近的K个样本，这里的距离公式使用的是欧氏距离，如式（1）所示。

式中，n表示特征向量的维数；xrj和xir分别代表xj和xi的第r个属性值。

当找到了K个最近邻样本，为了保证预测模型的正确性，输入程序的过程类标签由K个最近邻的类标签与它们的权重相乘并且相加起来得到。距离待划分过程越近的过程，给它所赋予的权重就越大，而且要随着特征向量间的距离增大，权重必须迅速衰减，但总权重必须为1。为了给K个最近邻的类标签分配权值，引入了式（2），它是指数级函数ex的麦克劳林级数。

式（2）中的x设定为1，然后再把公式两边除以e，就会获得式（3）：

基于式（3），可以推出分配的权重公式如下所示：

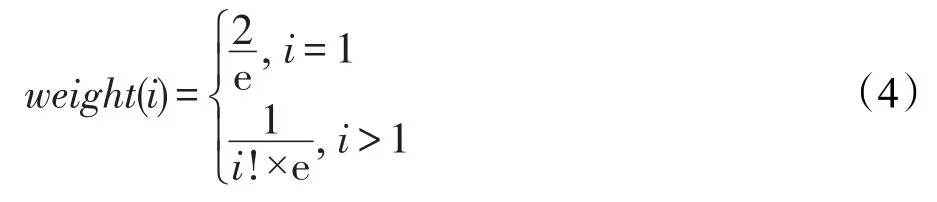
式（4）中的i表示待划分的过程与K个最近邻样本距离远近的顺序标号。距离越近分配的权重越大，因为使用的是Olden测试集，样本集数量并不是很多，所以把K个最近邻样本中的K值设定为10，即只考虑距离待划分过程的最近10个过程，加权求取待划分过程的方案。

由于目标函数Hpar是线程的划分方案，其类标签对应的是5个阈值。对于一个待划分的过程xq，其类标签是K个最近邻过程的类标签与它们各自的权重值之积并且相加，如式（5）所示：

式（5）中ĥj(xq)表示待划分过程的划分方案的第j个阈值；hj(xi)表示在训练样本中距离待划分过程的由近及远顺序的第i个过程的第j个阈值；weight(i)则是第i个过程的权重公式。

算法1基于KNN的划分方案的预测算法

输入：训练样本（X代表特征向量，H代表划分框架），xq新程序特征向量。

4.4 线程划分过程

对于一个待划分程序，已经获取其划分方案，接下来就是运用划分方案进行线程划分。线程划分是在程序的CFG（control flow graph）上进行的。首先需要对程序的循环区域进行划分，循环区域划分情况比较复杂，因为循环可以分为内层循环和外层循环，需要对它们分别进行线程划分。当完成对循环区域线程划分后，接下来就是将程序CFG中的循环区域归结成超级块，则原来的程序CFG变成了SCFG（super control flow graph）。然后在SCFG选取推测路径，根据代价评估模型对非循环区域进行线程划分。最后还需要为每个已划分好的线程构造预计算片段，最终完成对程序的线程划分。线程划分的加速过程如图6所示。

Fig.6 Effect of thread level speculation图6 线程级推测加速效果

4.5 代价评估模型

在建立代价模型时，需要假设存在无限个处理器核数，这样就不用考虑因处理器核数不足而产生线程撤销问题。在Prophet编译系统中，每条指令只占一个时钟周期，因此程序片段的执行时间可以用片段中包含的指令条数表示。在一个线程执行过程中，激发一个新的线程，激发路径上有3条相关指令，如图6所示。当这两个线程并行推测执行时，即父线程在一个处理器核上执行，子线程在另外一个处理器核上执行时，子线程首先需要执行预计算片段，预计算长度表示为pslice，父线程到子线程的激发距离为sp_dis，激发路径上包含的相关指令条数为dep_cnt，那么pslice可以用dep_cnt+C来表示，其中C表示创建预计算片段的开销。从图6可以得出子线程的提取执行时间，如式（6）所示：

式（6）只能体现出局部的加速效果，如果想得到全局的加速效果，即得到每条指令加速效果，则需要对提前的时间除以推测线程的指令条数。对于非循环区域划分评价的定义如式（7）所示：

式中，w为权重因子；thread_size为推测线程的指令条数；evalue为评估值。

针对非循环区域划分，首先提取程序的各个过程的特征，运用机器学习的方法从已构建好的TLS样本集中预测程序的各个过程较优的划分方案，而预测的划分方案由LLoTG、ULoTG、DDC、LLoSD、ULoSD组成。划分方案就是对候选线程的一组约束条件，对程序进行线程划分过程中，候选线程需要满足线程粒度、数据依赖数和激发距离这一组约束条件，并在满足约束条件的情况下，每次划分都是选择evalue值最大的点作为线程划分的边界。

4.6 循环划分

在开始对循环区域进行划分之前，首先需要归结循环区域为一个超级块，如图7所示。图7（a）中各个节点代表基本块，节点5→6→8→7→…→5→…是一个循环结构，可以归结为一个超级节点（即图（b）中灰色节点5′）。在循环归结后，本文开展循环的划分。为了充分挖掘循环区域的并行，对循环部分实行多处划分。本文对循环的划分分为两类，即循环嵌套迭代划分和循环内部划分。对于循环嵌套迭代，本文使用顺序激发方式对其进行划分，即第i次循环迭代激发第i+1循环迭代(i∈N)。如果循环包含的指令条数较多，使用非循环划分方法进行划分。

算法2循环区域划分算法

输入：循环入口节点。

输出：已划分的循环区域。

Fig.7 Progress of thread partitioning图7 线程划分过程

图8是一个循环划分示意图，用于解释循环区域划分算法。如果循环体大于线程粒度上限h2，对循环体执行非循环的划分；如果是嵌套循环，首先找出最可能路径，计算最优依赖opt_ddc，表达内层循环的指令数为size_of_loop以及激发距离spawn_dis；如果opt_ddc小于依赖数阈值h3，且size_of_loop取值在[h1,h2]之内，spawn_dis在[h4,h5]之内时，创建一个新线程。图8中包含了内层循环和外层循环，循环嵌套迭代显示在虚线框里，而外层循环部分包含了较多的指令条数。为了挖掘程序的潜在并行性，本文在循环多处进行划分，如果循环体过小，循环需要展开，然后按照非循环划分方法对展开的循环进行划分。最后识别回边，归结循环区域为内部循环，并对循环中连续迭代间数据依赖数进行检查，如果在下一次循环迭代处开始一个线程是有利的，则在下一次循环迭代处创建一个新的线程。

Fig.8 Diagram of loop partitioning图8 循环划分示意图

图8中的虚线框部分经过循环归结，归结成一个节点，得到一个以节点1为循环的开始节点和以6→1为回边的外层循环区域。如果拿掉回边6→1，就得到一个非循环区域，这种情况使用非循环线程划分方法进行划分。

4.7 非循环划分

算法3非循环区域的划分算法

在该代码中，curr_thread代表当前候选线程子图，是当前线程开始基本块（start_block）与上一个候选线程结束点之间的基本块集合。由于数据依赖过大或者线程体太小，curr_thread中子图不能单独作为一个线程；如果start_block和上一线程end_block重合，则curr_thread为空。start_block的最近后向支配节点用pdom_block表示，start_block和pdom_block之间的推测路径子图用path表示。线程划分过程中参考线程子图中粒度和激发距离。线程子图的粒度根据最大阈值h2和最小阈值h1，分为在粒度适中、粒度偏大、粒度偏小3种情况下如何划分非循环区域。在图9中，假设线程划分的关键路径是0—1—3—4—5—6。

（1）如果当前线程（0—1）粒度在区间 [h1,h2]之内，且激发距离在区间[h4,h5]之内，并且它和后继线程的数据依赖度不大于依赖数上限h3，则创建一个新的线程，如图9（a）所示。

（2）如果当前线程粒度偏大，即粒度在区间[h2,+∞)，则需要二次划分start_block和pdom_block间的区域。对于基本块0、1和2构成的子图，如果基本块0的粒度在[h1,h2]之内，并且与基本块1到future_thread之间区域数据依赖数小于h3，则可以在基本块1开始处创建一个新线程，如图9（b）所示。

（3）如果当前线程粒度偏小，即粒度在区间(0,h1]，那么加入curr_thread子图中的有path及pdom_block，同时分析划分pdom_block的后向支配节点到end_block之间的域。此时，如果线程粒度和数据依赖度都符合要求，那么就在基本块5的开始处创建新线程，如图9（c）所示。

5 实验评测

5.1 基准程序

本文主要使用Olden基准程序[24]作为测试用例，Olden测试集是Princeton大学提供的开源的C语言程序测试包。Olden测试集不是以数值计算为主的应用程序，其中包含了链表、树、图等各种比较复杂的控制流结构和数据结构，并行编译器很难把这种非规则的程序自动并行化，而且Olden测试集是开源的代码，获取比较容易，因此选择Olden作为测试程序。Olden基准测试程序如表2描述。

Table 2 Descriptions of Olden benchmarks表2 Olden基准程序描述

5.2 实验结果

Fig.9 Diagram of nonloop partition图9 非循环划分示意图

基于程序特征的线程划分方法，首先需要提取程序各个过程的特征，然后在已构建好的样本集中学习线程的划分方案，最后运用划分方案对程序进行线程划分。本文使用Olden测试集中程序的每个过程作为样本，通过对程序中每个过程的特征组建，得到每个过程的特征向量，然后运用专家经验显示划分的方法，获取程序中每个过程的最佳划分方案，这样样本就以“特征向量+划分方案”形式表示，将所有的样本组合到一起就构成了样本集。

本文采用KNN算法获取待划分程序中每个过程的划分方案。因为测试集和训练集使用相同的样本集，所以使用“留一法”对机器学习进行有效性验证。所谓的“留一法”就是当测试Olden中的某个样本时，这个样本不能从样本集中直接获取，只能通过机器学习从其他样本中预估得到。下面将以Olden中mst基准测试程序为例，展示预测mst程序中的每个过程的划分方案（依次表示线程间依赖数、线程粒度下限、线程粒度上限、激发距离上限、激发距离下限），如表3所示。首先剔除样本集中mst程序的每个过程的样本，避免加载自身的最优划分方案，然后提取mst程序中的每个过程的特征，从样本集中学习得到每个过程的预测划分方案。

Table 3 Partition schemes of samples and predictive partition schemes表3 样本中的划分方案与预测的划分方案

接下来将用预测的划分方案进行线程划分，为了说明方便，以mst基准测试程序的HashDelete过程为例，进行线程划分结果的展示。从预测划分方案可知，划分的线程间最大依赖数为3，线程粒度下限为9，线程粒度上限为45，激发距离下限为4，激发距离上限为20，其展示如图10所示。

Fig.10 Partition diagram of HashDelete in mst图10 mst的HashDelete过程的划分示意图

5.3 性能比较与分析

在基于程序特征的线程划分过程中，首先是获取程序特征，然后从样本集中用机器学习的方法获取划分方案，即一组阈值，程序中的每个过程有一组不同的阈值，然后用这组阈值进行线程划分，最后把划分后的线程放在Prophet模拟器上执行，获取每个程序的加速比。表4给出了基于启发式规则的划分方法、基于专家经验的划分方法和基于程序特征的划分方法的加速比结果，其中Prophet模拟器的核数设置为4。

为了展示基于程序特征的线程划分的有效性，本文选择与原始基于启发式规则的线程划分方法进行比较。因为基于专家经验的划分是一种显式的划分方法，它可以根据程序的控制依赖和数据依赖关系选择合适的线程边界，并且可以多次调整sp、cqip点的位置，一般情况下获取的加速比都要好于隐式划分，所以表4中的基于专家经验获取的加速效果比基于启发式和基于程序特征的加速效果好。但基于专家经验的线程划分方法需要人工选择线程边界，如果全部使用这种方法划分所有的串行非规则程序，基本上不可能实现，而Olden基准程序集包含的程序并不多，通过手工标注线程边界是可行的，使用这种方法只是用来获取线程较优划分方案，构造TLS样本集。因此进行实验结果分析时，只比较基于原始的启发式规则和基于程序特征的线程划分方法的性能。接下来将对实验结果进行分析，只选取Olden基准程序集中的几个程序进行分析。

Table 4 Comparison results of speedups表4 加速比对比结果

程序bh主要的数据结构是异构八叉树，存在着非常复杂的数据依赖关系，它的并行性既存在于循环结构，也存在于非循环结构。对于启发式规则，使用相同的划分方案划分bh程序所有的过程，而对于基于程序特征的划分方法，可以为程序中的每个过程预测出与自身特征相匹配的划分方案，然后进行线程划分，但因为存在较多的依赖关系，所以最终只获得了19.54%的性能提升。

程序em3d的主要数据结构是单向链表，其中循环结构占据绝大部分，因此程序em3d的并行性主要来自于循环结构。虽然基于程序特征的线程划分方法可以获取适合自身特征的划分方案，但对循环区域的特征提取不够充分，最终与启发式划分方法相比，仅仅获取了13.17%的性能提升。

程序health的主要数据结构是双向链表，其中包含了循环结构和非循环结构。循环结构是并行性的主要来源，与启发式规则相比，程序health可以获取适合其特征的划分方案。对循环区域进行划分，虽然循环占据程序的大部分，但分析其循环区域，发现循环体较大，数据依赖简单，因此程序health获取了18.27%的加速效果。

程序perimeter的主要数据结构是四叉树，程序中都是非循环结构，没有循环结构。程序的并行性主要来自于函数以及函数体分解成多线程。因为很难预测函数的返回值，所以这两种划分方法加速比效果都不好。和启发式规则相比，基于程序特征的划分方法为程序的每个过程选择符合自身特征的划分方案，并且划分方案不受循环影响，对于非循环域采用的评估模型，为当前程序找到较好的线程划分边界，因此最终程序执行性能提升了18.23%。

程序treeadd的主要数据结构是二叉树，程序结构简单，其中只包含4个过程，而且程序中并不包含任何循环结构，只有非循环结构，因此并行性都来自于非循环区域。通过基于程序特征的划分方法可以为每个过程选取合适的划分方案，但treeadd中存在较多递归函数调用和数据依赖，最终程序获得了21.19%的性能提升。

程序bisort的主要数据结构是二叉树，本文通过对源码的分析可知，程序中只包含3个循环体，并且执行的只有2个循环体，而且循环体粒度都比较小。那么程序的并行性主要来自于非循环区域，虽然程序存在一定数量的数据依赖，但通过基于程序的特征划分方法可以从程序中挖掘潜在的并行性，选择程序中各个过程合适的划分方案，对于非循环域采用评估模型，找到了较好的线程划分边界，最终基于程序特征的划分方法获取了27.47%的性能提升。

图11展示了基于启发式与基于程序特征的划分方法获取的加速比对比图。从图11中可以观察出，本文基于程序特征的线程划分方法在Olden测试集上的加速比与基于启发式规则划分方法的加速比在不同程度上都有一定的提高，但不同的程序，加速比性能提升幅度有比较明显的差异。总体来说，原始的基于启发式规则的平均加速比为1.725，而本文基于程序特征的平均加速比为2.040，平均加速比提升了18.24%，这说明基于程序特征的线程划分方法对程序划分有较好的效果。图12显示了部分SPEC2000和Olden基准程序在不同核个数上执行的加速比。

Fig.11 Comparison of speedups for Olden benchmarks图11 Olden测试集加速比对比图

Fig.12 Comparison of speedups for Olden and SPEC2000 benchmarks over different PEs图12 Olden和SPEC2000测试程序在不同核数上的加速比对比图

6 总结和展望

6.1 总结

本文在Prophet系统基础上，提出了一种基于程序特征的线程划分方法，将机器学习方法运用到线程划分中。根据程序特征从样本集中预测线程的划分方案，并利用预测的划分方案进行线程划分，最后在Prophet模拟器上执行划分后的程序，验证其执行性能。本文的研究内容和相关结论如下。

（1）构建TLS样本集

本文提出了构建TLS样本集的方法。TLS样本集是由特征和划分方案组成。特征是在程序的每个过程的控制流图的推测路径上提取的。对于TLS样本中划分方案获取方法，采用了一种基于专家经验显式划分的方法，对程序进行显式划分，统计出程序中每个过程的较优划分方案。

（2）预测划分方案

本文使用了机器学习中的KNN分类算法从已构建的TLS样本集中获取待划分程序的每个过程的较优划分方案。

（3）基于程序特征的线程划分

本文提出了一种在获取程序的每个过程的划分方案的基础上，利用划分方案对程序进行划分的方法，并分别进行了程序的非循环区域划分和循环区域划分。针对程序的非循环区域，建立一个评估模型，并根据评估模型对非循环区域进行迭代划分。针对循环区域，则分别进行循环嵌套迭代和循环内部划分。对于嵌套循环，采用顺序激发、嵌套迭代方式进行线程划分；对于循环内部，则采用基于非循环区域划分的方法进行线程划分。

（4）使用Olden基准程序进行测试

使用Olden基准程序在Prophet系统上验证基于程序特征的线程划分的效果，并与原有的划分结果进行比较。测试结果表明，根据程序特征获取划分方案，并用划分方案进行线程划分的程序执行加速比与原始的加速比平均提升了18.24%。

6.2 展望

随着TLS的快速发展和人们对并行计算的关注增加，基于TLS的算法逐渐成为研究的热点。在算法层次实现线程级推测，从而实现更高抽象层次来开发并行性，克服了编程方面的一些困难。

在平台方面，TLS逐渐从单机多核发展成分布式平台，如Spark平台上的解压算法的线程级推测并行。

:

[1]Schaller R R.Moore’s law:past,present,and future[J].IEEE Spectrum,1997,34(6):52-59.

[2]Thompson S E,Parthasarathy S.Moore’s law:the future of Si microelectronics[J].Materials Today,2006,9(6):20-25.

[3]Shoji Y,Nunome A,Hirata H,et al.A large-scale speculation for the thread-level parallelization[C]//Proceedings of the 3rd International Conference on Applied Computing and Information Technology/the 2nd International Conference on Computational Science and Intelligence,Okayama,Jul 12-16,2015.Washington:IEEE Computer Society,2015:162-168.

[4]Estebanez A,Llanos D R,González-Escribano A.A survey on thread-level speculation techniques[J].ACM Computing Surveys,2016,49(2):1-39.

[5]Hammond L,Hubbert B A,Siu M,et al.The Stanford hydra CMP[J].IEEE Micro,2000,20(2):71-84.

[6]Sohi G S,Breach S E,Vijaykumar T N.Multiscalar processors[C]//Proceedings of the 22nd Annual International Symposium on Computer Architecture,Santa Margherita Ligure,Jun 22-24,1995.Washington:IEEE Computer Society,1995:414-425.

[7]Liu Wei,Tuck J,Ceze L,et al.POSH:a TLS compiler that exploits program structure[C]//Proceedings of the 2006 ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming,New York,Mar 29-31,2006.New York:ACM,2006:158-167.

[8]Deng Kun.Research and implementation of multithread compiler optimization technology[D].Changsha:National University of Defense Technology,2001.

[9]Steffan J G,Colohan C B,Zhai A,et al.The STAMPede approach to thread-level speculation[J].ACM Transactions on Computer Systems,2005,23(3):253-300.

[10]Quiñones C G,Madriles C,Sánchez F J,et al.Mitosis compiler:an infrastructure for speculative threading based on pre-computation slices[C]//Proceedings of the 2005 ACM SIGPLAN Conference on Programming Language Design and Implementation,Chicago,Jun 12-15,2005.New York:ACM,2005:269-279.

[11]Madriles C,Quiñones C G,Sánchez F J,et al.Mitosis:a speculative multithreaded processor based on precomputation slices[J].IEEE Transactions on Parallel and Distributed Systems,2008,19(7):914-925.

[12]Ohsawa T,Takagi M,Kawahara S,et al.Pinot:speculative multi-threading processor architecture exploiting parallelism over a wide range of granularities[C]//Proceedings of the 38th Annual IEEE/ACM International Symposium on Microarchitecture,Barcelona,Nov 12-16,2005.Washington:IEEE Computer Society,2005:81-92.

[13]Chen Zheng,Zhao Yinliang,Pan Xiaoyu,et al.An overview of Prophet[C]//LNCS 5574:Proceedings of the 9th International Conference on Algorithms and Architectures for Parallel Processing,Taibei,China,Jun 8-11,2009.Berlin,Heidelberg:Springer,2009:396-407.

[14]Song Shaolong,Zhao Yinliang,Feng Boqin,et al.Prophet+:an extended multicore simulator for speculative multithreading[J].Journal of Xi’;an Jiaotong University,2010,44(10):13-17.

[15]Dong Zhaoyu,Zhao Yinliang,Wei Yuanke,et al.Prophet:a speculative multi-threading execution model with architectural support based on CMP[C]//Proceedings of the International Conference on Scalable Computing and Communications/the 8th International Conference on Embedded Computing,Dalian,Sep 25-27,2009.Washington:IEEE Computer Society,2009:103-108.

[16]Johnson T A,Eigenmann R,Vijaykumar T N.Min-cut program decomposition for thread-level speculation[C]//Proceedings of the 2004 ACM SIGPLAN Conference on Programming Language Design and Implementation,Washington,Jun 9-11,2004.New York:ACM,2004:59-70.

[17]Codrescu L,Wills D S.On dynamic speculative thread partitioning and the MEM-slicing algorithm[C]//Proceedings of the 1999 International Conference on Parallel Architectures and Compilation Techniques,Newport Beach,Oct 12-16,1999.Washington:IEEE Computer Society,1999:40-46.

[18]Wang Zheng,O'Boyle M F P.Mapping parallelism to multicores:a machine learning based approach[C]//Proceedings of the 14th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming,Raleigh,Feb 14-18,2009.New York:ACM,2009:75-84.

[19]Grewe D,Wang Zheng,O'Boyle M F P.A workload-aware mapping approach for data-parallel programs[C]//Proceedings of the 6th International Conference on High Performance Embedded Architectures and Compilers,Heraklion,Jan 24-26,2011.New York:ACM,2011:117-126.

[20]Long Shun,Fursin G,Franke B.A cost-aware parallel workload allocation approach based on machine learning techniques[C]//LNCS 4672:Proceedings of the 2007 International Conference on Network and Parallel Computing,Dalian,Sep 18-21,2007.Berlin,Heidelberg:Springer,2007:506-515.

[21]Li Yuxiang,Zhao Yinliang,Wu Qiangsheng.A graph-based thread partition approach in speculative multithreading[C]//Proceedings of the 18th IEEE International Conference on High Performance Computing and Communications,the 14th IEEE International Conference on Smart City,the 2nd IEEE International Conference on Data Science and Systems,Sydney,Dec 12-14,2016.Piscataway:IEEE,2017:406-413.

[22]Li Yuxiang,Zhao Yinliang,Shi Jiaqiang.A hybrid samples generation approach in speculative multithreading[C]//Proceedings of the 18th IEEE International Conference on High Performance Computing and Communications,the 14th IEEE International Conference on Smart City,the 2nd IEEE International Conference on Data Science and Systems,Sydney,Dec 12-14,2016.Piscataway:IEEE,2017:35-41.

[23]Carlisle M C,Rogers A,Reppy J H,et al.Early experiences with Olden[C]//LNCS 768:Proceedings of the 6th International Workshop on Languages and Compilers for Parallel Computing,Portland,Aug 12-14,1993.Berlin,Heidelberg:Springer,1993:1-20.

[24]Carlisle M C.Olden:parallelizing programs with dynamic data structures on distributed-memory machines[D].Princeton:Princeton University,2010.

附中文参考文献：

[8]邓鹍.前瞻多线程编译优化技术的研究与实现[D].长沙:国防科学技术大学,2001.

[14]宋少龙,赵银亮,冯博琴,等.支持推测多线程的扩展多核模拟器Prophet+[J].西安交通大学学报,2010,44(10):13-17.