一种宽带高斯白噪声的设计与实现

石远东，卢雪怡，李 霄

(1.中国船舶重工集团公司第七二三研究所,江苏 扬州 225101；2.江苏科技大学，江苏 镇江 212003)

0 引 言

干扰目前主要分为遮盖性干扰和欺骗性干扰。遮盖性干扰就是利用高干信比的噪声信号遮盖住目标回波，从而使雷达无法正常检测目标。雷达接收机处理的信号是含有加性噪声的，噪声的随机性越强，检测结果的不确定性越高。在相同功率条件下，当噪声信号服从高斯分布时，其不确定性最高，为最佳遮盖干扰波形[1]。

高斯白噪声可以通过模拟或数字的方法产生,目前的研究主要是基于数字合成方法开展的。数字合成的一般方法是先产生均匀分布的白噪声,然后通过转换将均匀分布变为高斯分布从而得到高斯白噪声。文献[2]首先采用Tausworthe算法生成均匀分布的白噪声,然后通过查表法实现均匀分布白噪声到高斯白噪声的转化。文献[3]则先采用lagged-Fibonacci算法生成均匀分布的随机序列,然后通过公式法产生高斯白噪声。而文献[4]利用M序列发生器产生均匀分布随机数,通过15段折线逼近法实现了高斯白噪声序列。

本文主要介绍了一种基于高性能现场可编程门阵列(FPGA)和高速数模变换器(DAC)的宽带高斯白噪声的快速产生方案。首先通过M序列发生器产生伪随机序列，利用并行取样的方法降低随机数的相关性，再将数据送入系数可重新配置的多相滤波器，最后将多相滤波器输出数据进行并串转换后送高速DAC。设计方案首先使用 Matlab进行仿真验证,然后采用VerilogHDL进行软件编程和Modelsim仿真验证,最终在印制板上进行了测试，验证了方案的可行性。

1 基本理论

1.1 噪声最佳干扰波形

衡量随机变量不确定性的量是熵，对于连续型随机变量：

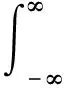
(1)

式中：p(x)为随机变量的概率分布密度函数。

当a取一确定值时，熵值越大，则说明随机信号的不确定性越强；同时熵值还与随机信号的方差(平均功率)有关，方差越大，熵值也越大。因此噪声的最佳干扰波形就是在噪声功率限定的条件下，具有最大熵值的概率分布的噪声信号。

根据Lagrange常数变易法，已知函数方程：

(2)

以及对应的n个函数方程的约束条件：

(3)

式中：φ1，φ2，…，φn为约束条件中给定的函数，则式(2)的最值可以由式(3)的n个方程和下式决定：

(4)

式中：λ1，λ2，…，λn为拉格朗日常数。

代入最大熵函数求解，取a=e，则已知：

(5)

从而有：

(6)

p(x)=eλ1-1+λ2x2

(7)

利用限制条件，可以得到：

(8)

(9)

因此，在噪声功率限定的条件下，当噪声服从高斯分布时，其熵值最大，是噪声最佳干扰波形。

1.2 M序列发生器

伪随机序列是具有某种随机特性的确定的序列，它既具有随机统计特性，又可以重复产生，因此获得了广泛的应用。M序列就是一种常用的伪随机序列,它是最长线性反馈移位寄存器的简称。M序列自Shannon信息论诞生后得到了广泛研究，目前理论比较成熟，已得到广泛应用。线性反馈移位寄存器是产生M序列的主要功能模块，如果线性反馈移位寄存器选择的级数是n，则M序列的重复周期为2n-1。将M序列产生的数据看成无符号整数，则数据的取值范围为1～2n-1，并且在一个重复周期内，每一个无符号整数出现且只出现一次。因此利用M序列产生的数据是服从均匀分布的随机数。

产生M序列的反馈移位寄存器的递归方程是：

an=cn-1an-1⨁cn-2an-2⨁...⨁c1a1⨁c0a0

(10)

式中给出了移位输入an与移位前各级状态a0,a1,…,an-1的关系。反馈系数c0,c1,…,cn-1确定了移位寄存器的反馈连接和序列的结构，取值为0或1。取值为0表示对应的移位寄存器无馈线运算，取值为1表示对应的移位寄存器参与反馈运算。反馈系数的取值可通过查找本原多项式来得到。n的取值决定了M序列的重复周期，为了使M序列的重复周期足够长以满足噪声的设计要求，选取n=31，则序列周期可达2.147×109，FPGA系统时钟为250 MHz，噪声重复周期可达到8.59 s。

1.3 降低相关性处理

高斯白噪声信号是一个随机过程，假设其双边功率谱密度为常数N0,由于信号的自相关函数是功率谱密度的傅里叶反变换，将N0进行傅里叶反变换，得到高斯白噪声的自相关函数为：

R(τ)=N0×δ(τ)，-∞<τ<+∞

(11)

由式(11)可见，高斯白噪声的自相关函数是一个δ(τ)的函数，在任意2点不同时刻的采样值的自相关值是零，这2个采样值是完全独立的。线性反馈移位寄存器每一节拍只将最高位an-1移出，并将反馈值an送给最低位a0。所以相邻的采样值仍然具有一定的相关性，不是完全独立的。为了减小相邻信号的相关性，需要做去相关处理。文献[4]介绍了通过间隔r个时钟周期(r=2i)进行采样状态值的方法来降低随机序列的相关性。

本文采用的是多路M序列并行产生随机数的方法。当需要产生10 bit位的随机数据时，使用10路M序列发生器并行处理，将10路M序列的最高位同时提取出来组成一个10 bit数据。这样的10 bit数据只选取了每个M序列的一个状态值，因此相邻的数据是完全独立的，没有相关性。这10路M序列发生器需配置不同的反馈系数，初值可以一样。图1分别显示了单个M序列发生器产生10 bit随机数和10路M序列发生器并行处理产生10 bit随机数的功率谱。由图1可知，采用M序列发生器并行处理产生的随机数的功率谱基本水平。将功率谱进行傅里叶反变换，得到的信号近似一个δ(τ)的函数，表明M序列发生器并行处理产生的随机数任意2个不同时刻的采样信号是相互独立的，证明该方法降低随机序列的相关性是有效的。

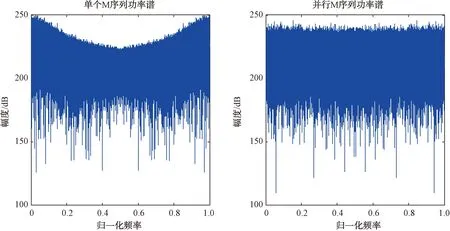
图1 M序列功率谱

1.4 多相滤波处理

多路M序列并行产生随机数的功率谱是基本水平的，要生成带宽可调的数字噪声序列需对产生的随机数进行数字滤波,本文采用的是有限冲激响应(FIR)数字滤波器。根据中心极限定理(CLT)，大量独立同分布的随机变量之和必定是一个正态随机变量。因此均匀随机分布的随机数经过FIR数字滤波器后转换成近似正态分布的随机数，而且随着滤波器阶数的增加,输出噪声的分布特性更接近高斯分布。FIR数字滤波器既实现了噪声带宽可调的功能，又完成了均匀噪声向高斯白噪声的转换。

由于本文设计的噪声数据率是2 Gsps，如此高速的数据无法用普通的FIR滤波器进行滤波，因此采用多相滤波器进行滤波。多相滤波的基本原理如下：设数字滤波器的冲击响应为h(n)，则其z变换H(z)定义为：

(12)

令n=mD+k(m=0,1，2，…，M-1；k=0,1，2，…，D-1；N=MD)，则式(12)可重新组织如下[5]：

(13)

(14)

式(14)为数字滤波器H(z)的多相滤波结构。在本文中N的值为32，D的值为8。图2为随机数经过FIR滤波器的输出频谱。

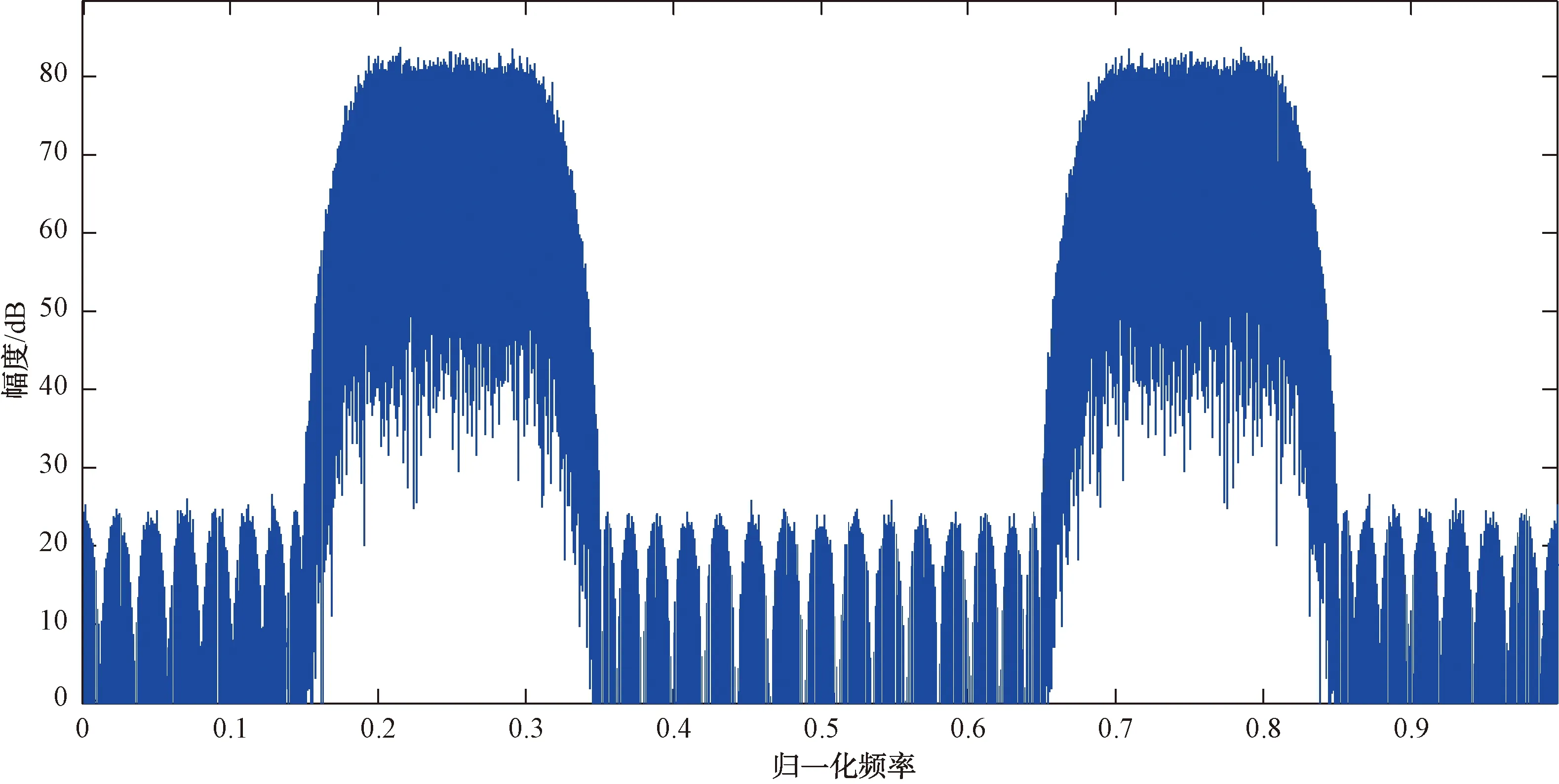
图2 随机数滤波后频谱

图3显示了随机数滤波前后的直方图，滤波前的随机数近似均匀分布，经过滤波器后随机数近似正态分布，即输出的信号是高斯白噪声。

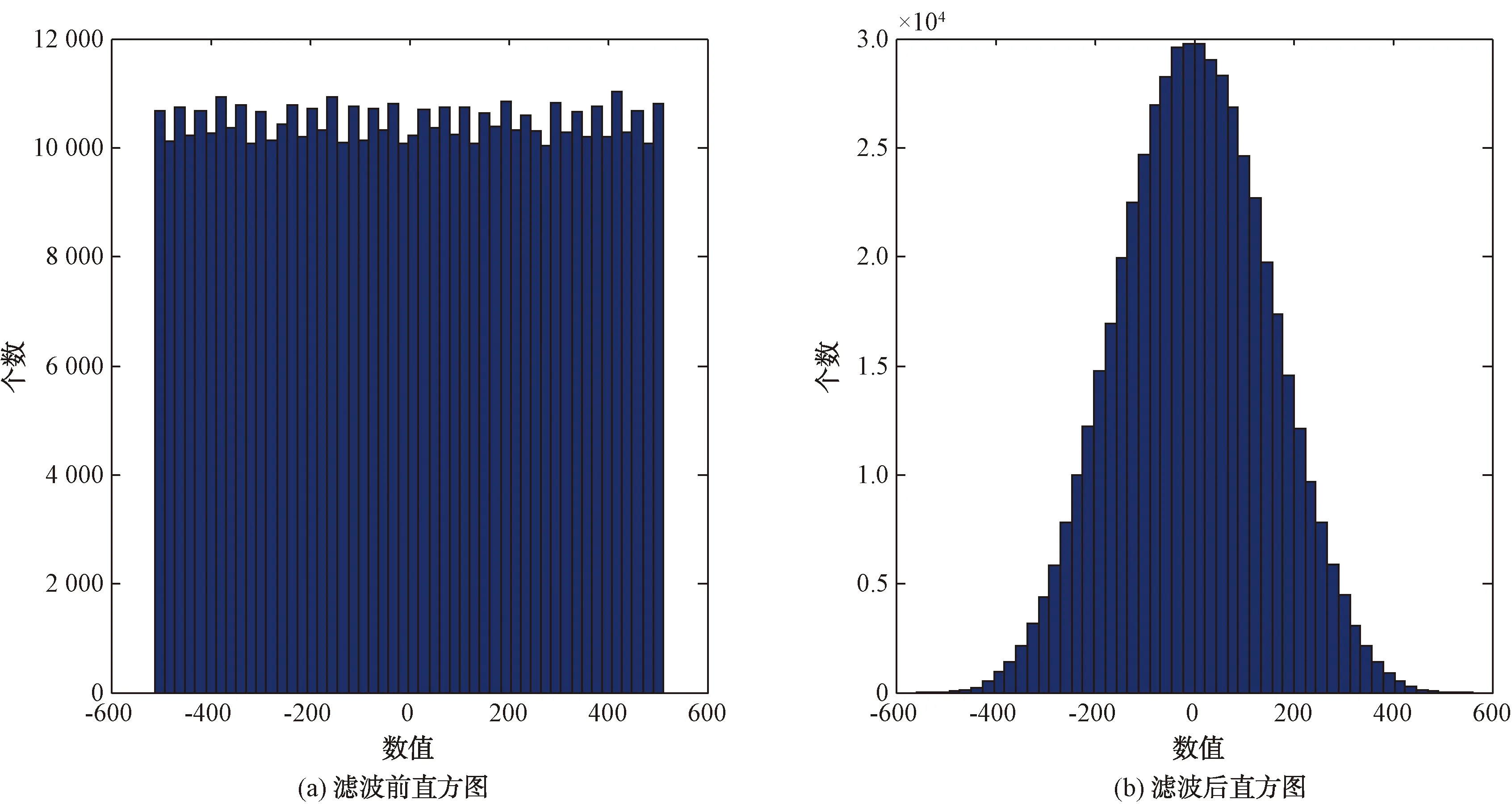
图3 随机数滤波前后直方图

2 软件设计

本设计选用的FPGA是Altera公司StratixIII系列的EP3SL340H1152I3。该芯片是一款高性能FPGA，具有丰富的逻辑资源，共有576个高速数字处理器(DSP)模块，拥有8个锁相环(PLL)，并且内嵌了18 Mbits的随机存取器(RAM)资源。高速DAC是E2V公司的EV10DS130AVZPY，最高数据转换速率可达3 Gsps，本设计中采用的转换率为2 Gsps。软件开发工具使用QuartusII和Modelsim进行设计和仿真验证。图4是FPGA设计原理框图。

图4 FPGA设计原理框图

首先进行M序列发生器和去相关模块的设计。利用Modelsim进行仿真验证，将仿真数据导入Matlab进行频谱和直方图分析，分析结果与图1及图3完全一致。然后进行FIR滤波器设计，将滤波器系数定义为输入变量，通过改变滤波器系数实现输出噪声中心频率和带宽的配置。图5中的M_Code[79..0]是经过滤波器后的8路10 bits并行噪声数据，将数据进行并串转换后送给高速DAC。

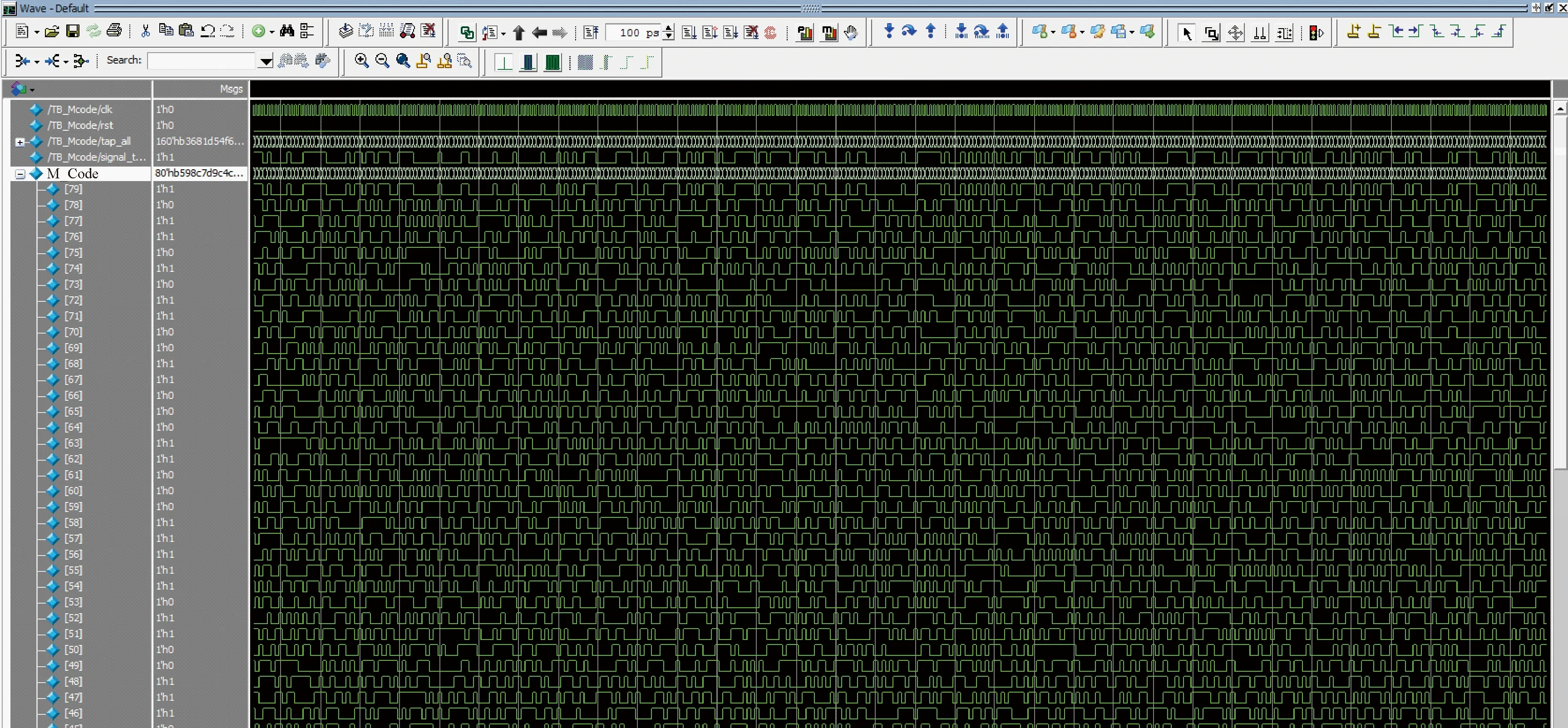
图5 滤波输出仿真图

3 实际测试

为了验证设计的正确性，将设计好的软件下载到硬件电路中进行测试。试验中系统时钟250 MHz，DAC时钟2 GHz，FIR滤波器设定中心频率500 MHz，带宽400 MHz。利用SignalTap采集FIR滤波器后的数据，并导入Matlab进行频谱和直方图分析。分析结果同图2、图3完全一致。将DAC输出信号分别接入示波器和频谱仪，观察信号的时域、频域波形。图6、图7分别是示波器和频谱仪的显示波形，从图7可以看出，信号3 dB带宽为407 MHz，带内平坦度为±1 dB。实测结果与理论分析一致，验证了该方案的准确性。

图6 输出时域波形

图7 输出频域波形

4 结束语

本文提出了一种宽带高斯白噪声的产生方法，利用M序列发生器产生伪随机序列，利用并行取样的方法降低随机数的相关性，再通过FIR数字滤波器实现噪声带宽及中心频率的配置，并完成了均匀噪声向高斯白噪声的转换。该设计方法在FPGA和高速DAC的平台上进行了测试，产生了比较理想的宽带高斯白噪声，证明了设计方法的可行性和正确性。本设计可以应用在有源干扰机的工程实践中，具有很好的实用价值。

[1] 赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社，2003.

[2] 黄本雄,侯洁,胡海.高斯白噪声发生器在FPGA中的实现[J].微计算机信息,2007,23(7-2):165-167.

[3] 蒋乐,冯文全.高性能可编程高斯白噪声的设计与实现[J].电子技术应用,2006(8):113-114.

[4] 管宇,徐雷,徐建中.用FPGA产生高斯白噪声序列的一种快速方法[J].电子元器件应用,2008,10(11):55-58.

[5] 杨小牛，楼才义，徐建良.软件无线电技术与应用[M].北京:北京理工大学出版社,2010.