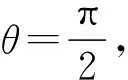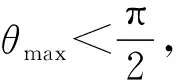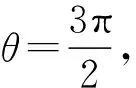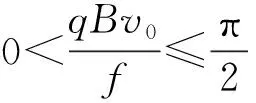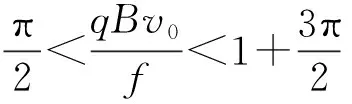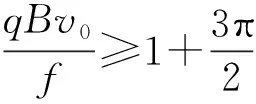带电粒子沿“渐开线”的运动
袁 平 李忠相 栾 丽
(重庆市第一中学校,重庆 400030)
带电粒子在匀强磁场中的运动,多次在高考和竞赛问题中出现.在备考过程中,已经总结出一系列经典情形:若粒子初速度与磁场方向平行,粒子做匀速直线运动;若粒子初速度与磁场方向垂直,粒子做匀速圆周运动;若粒子初速度与磁场方向有一定夹角,粒子做等距螺旋运动;若粒子初速度与磁场方向有一定夹角,且受到另一个沿磁场方向的恒力,粒子做不等距螺旋运动;若粒子初速度与磁场方向垂直,且受到另一个垂直于磁场方向的恒力,粒子沿滚轮线运动……
若粒子初速度与磁场方向垂直,且受到一个大小恒定但方向始终与速度方向相反的阻力,粒子又怎样运动呢?
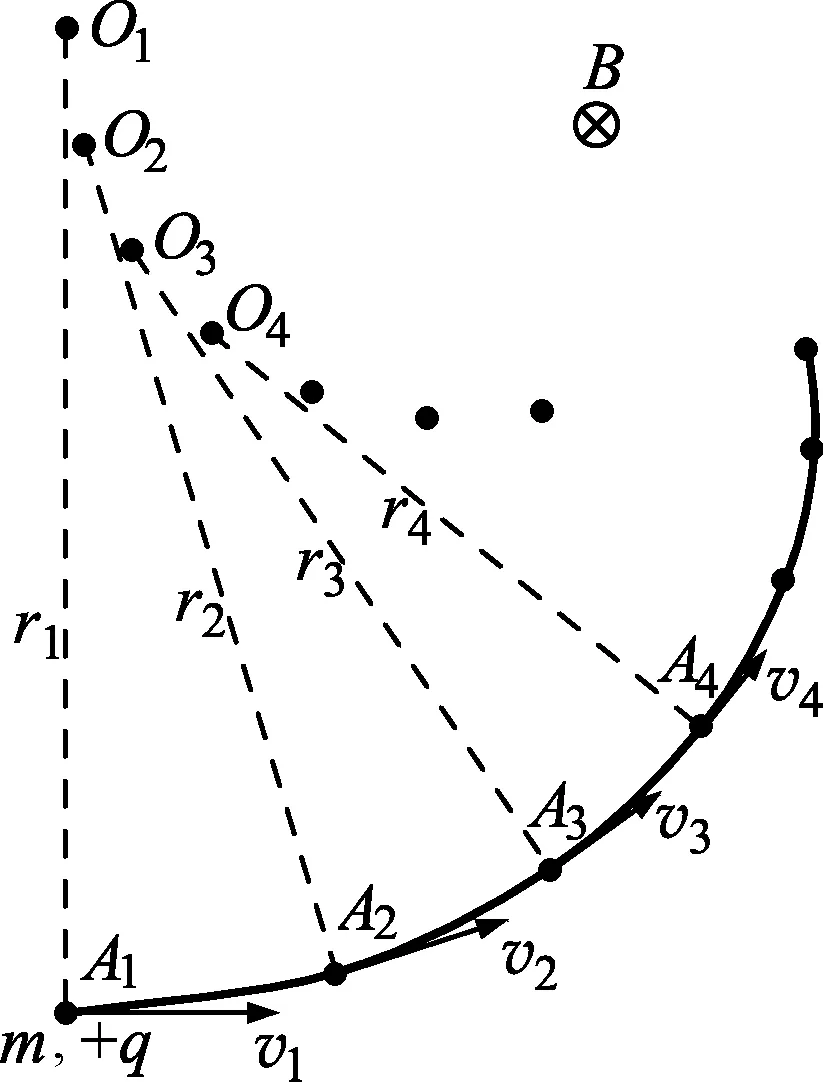
图1 轨迹分析图
例题.如图1所示,在垂直于纸平面向里的磁感应强度为B的匀强磁场中,有一质量为m、电荷量为+q的带电粒子以初速度v1从A1点出发,若运动过程中在纸平面内受到一个大小恒定为f、方向始终与速度方向相反的阻力.不计重力,粒子的运动规律如何?
易知,带电粒子的速度大小不受洛伦兹力影响,只在恒定大小的阻力f作用下均匀减小,其加速度大小记为a,显然
(1)
同时,带电粒子在洛伦兹力作用下,速度方向不断变化,当粒子速度为v时,其轨迹曲率半径为
(2)
可见,曲率半径受速度大小影响,亦均匀减小.至此,我们可以大致确定轨迹的形状.
为了定量研究粒子的轨迹,不妨取一系列极小连续相等的时间间隔Δt,经过第一个Δt后,粒子到达A2处,速度大小记为v2,轨迹曲率半径由r1变为r2,则速度和曲率半径的减小量分别为
Δv=v1-v2=aΔt.
(3)
(4)
相应地,轨迹的曲率圆心从O1点换至O2点,O1A1和O2A2之间的夹角为
(5)
如果把O1和O2之间用一小段圆弧连起来,则该段圆弧对应的圆心角也为Δθ,该段圆弧的弧长和曲率半径分别为
Δs=Δr.
(6)
(7)
由以上各式联立,可得
(8)
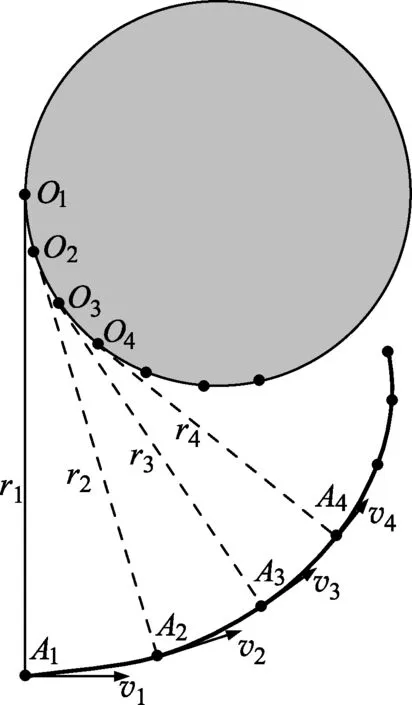
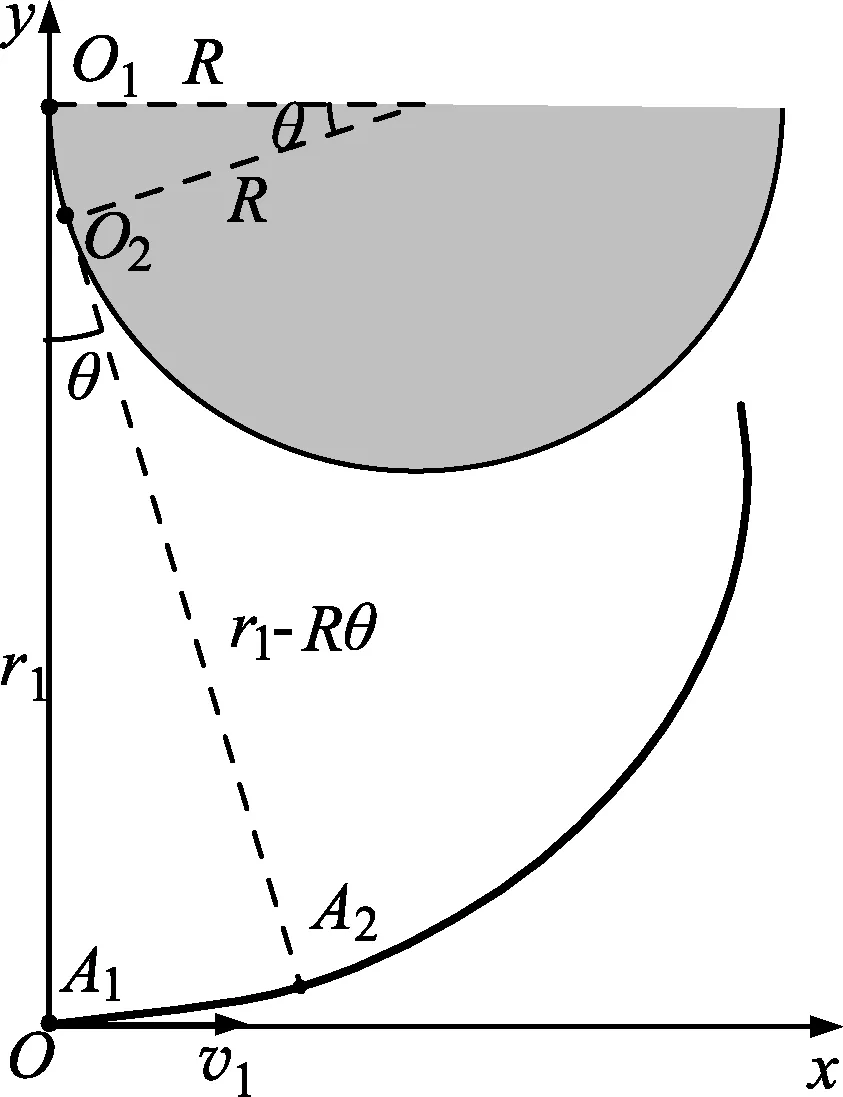
图2 渐开线
这表明,O1、O2之间的小段圆弧的曲率半径是一个与粒子速度无关的定值.那么,接下来相同时间间隔确定的O3、O4……之间连起来的小段圆弧具有相同的曲率半径,即O1、O2、O3……等所有轨迹瞬时中心构成一半径为R的圆弧.同时由(6)式可知,轨迹曲率半径r的减少等于轨迹瞬时中心O在圆弧上的移过路程.
上述轨迹,实际上就是著名的“渐开线”.如图2,一段长为r1的不可伸长的绳子,一端系在半径为R的固定圆柱的边缘O1点,另一端系一小球,小球以垂直于绳的初速度运动,绳将不断地绕在圆柱上,则该小球碰到圆柱前的轨迹与上述带电粒子的轨迹完全一样.
值得注意的是,虽然上述两种情况的轨迹完全一样,但运动时间可能不同.由于受细线约束,小球的速度大小无论以什么样的规律变化,其运动都在这条轨迹上.只有当小球速度大小也以加速度a均匀减小,才和带电粒子的运动规律完全一样.当轨迹和圆柱相交时,小球可能被圆柱弹回再将绳展开.而此时带电粒子轨迹的曲率半径已经为0,即粒子速度已减小到0,在默认阻力也随之消失的情况下,粒子即静止于此,运动过程结束.
同样地,如果带电粒子受到的不是阻力,而是大小恒定,方向始终与速度方向相同的动力,轨迹便是不断展开的“渐开线”.
这个带电粒子沿“渐开线”运动的问题从高考到竞赛决赛都可以涉及,为了更好地发挥它的教学价值,笔者尝试编制了以下习题,抛砖引玉.
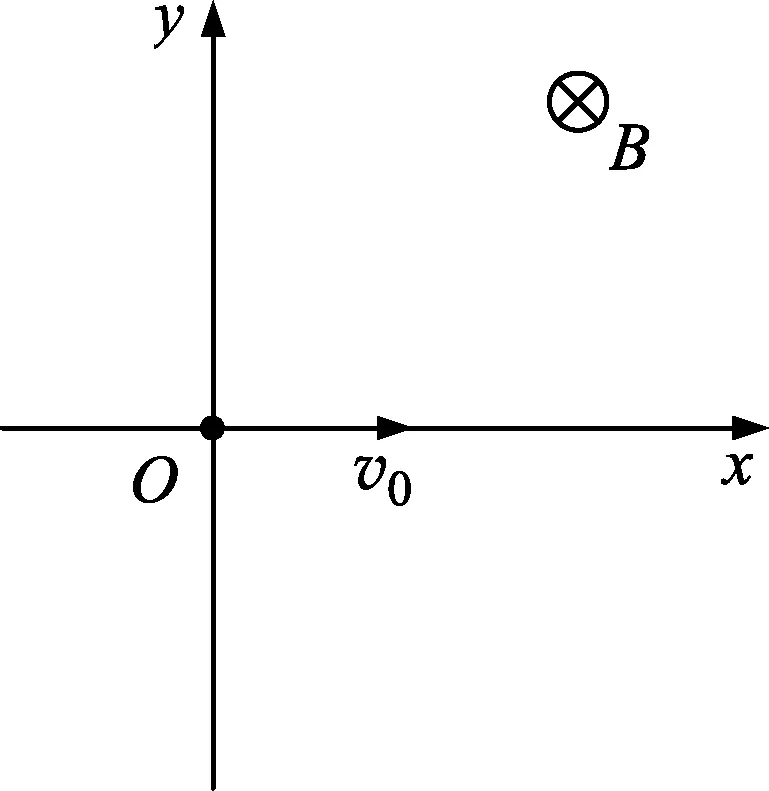
图3 习题图
习题.如图3所示,在O-xy平面内有垂直于平面向里的匀强磁场,磁感应强度为B.一质量为m、带电荷量为+q的粒子从O点沿x轴正方向以初速度v0开始运动,运动过程中受到一个大小恒定为f、方向始终与速度方向相反的阻力,不计重力.
(1) (高考难度)该粒子的运动轨迹可能是图4中的
(2) (竞赛预赛难度)从粒子经过O点开始计时,求t时刻粒子的速度大小及方向;
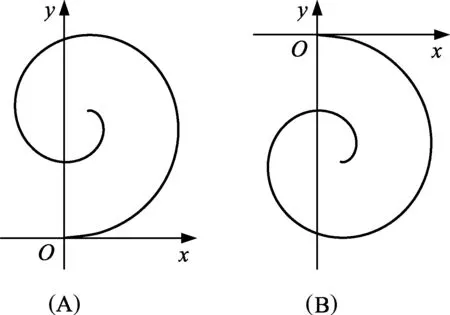
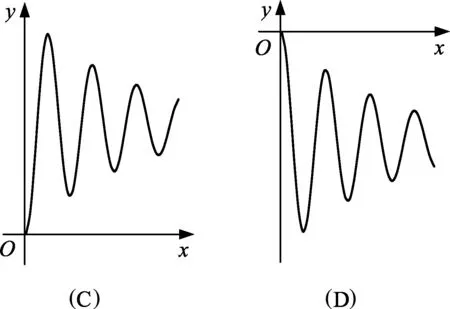
图4
(3) (竞赛复赛难度)求粒子运动的轨迹方程以及粒子最终的位置坐标;
(4) (竞赛决赛难度)求粒子运动过程中x坐标分量的取值范围.
解析: (1) 由于粒子速度不断减小,并结合洛伦兹力方向,不难判断(A)选项正确.
(2)由公式(1)可知,粒子运动的总时间为
(9)
当t (10) 由公式(2)可知,粒子速度方向随时间均匀增大,即t时刻,速度与x轴正方向夹角为 (11) 当t≥t0时,粒子的速度为0. (3) 由前文所述,粒子的运动轨迹为图2所示“渐开线”,其中初始绳长r1和圆柱半径R分别为 (12) 将缠绕的角度θ作为参数(如图5所示),可写出轨迹的参数方程,即 x=R(1-cosθ)+(r1-Rθ)sinθ, (13) y=r1-Rsinθ-(r1-Rθ)cosθ, (14) 其中r1和R由式(12)给出.t0时刻停止运动,由式(9)、(11)~(14)可得最终坐标为 (15) (16) (17) (18) (19) 综上,粒子运动过程中x坐标分量的范围为: 当然,这个问题如果不和“渐开线”类比,直接写微分方程亦可求解,但解题过程,尤其是一些分类讨论的临界情形不太直观. 参考文献: 1 张璋,张引红. 匀强磁场中不同受力下带电粒子的运动轨迹[J].物理教学,2017,38(6):65-67. 2 程稼夫.中学奥林匹克竞赛物理教程电磁学篇[M].合肥:中国科学技术大学出版社,2014:386-388.