基于小波变换的眼科光学相干层析图像降噪对比研究

罗曼婷，钟舜聪，张秋坤，林杰文，沈耀春，姚立纲

1.莆田学院 机电工程学院，福建 莆田 351100；2.福州大学 a.机械工程及自动化学院；b.物理与信息工程学院，福建 福州 350108；3.上海大学 机电工程及自动化学院，上海 200444

引言

光学相干层析（Optical Coherence Tomography，OCT）是二十世纪90年代以来迅速发展起来的一种扫描成像技术[1]。OCT素有“光学中的超声波”的美称，其成像机理类似于超声波，采用光波干涉原理代替声波来产生图像。光在被测样品内部散射，通过测量和处理反射回来的干涉光强，可形成高分辨率的深度图像，表达了样品的内在微观结构。该方法具有活检性，无需物理接触的优势。横向扫描可以快速地获取非侵入二维及三维图像，分辨率高。近年来，OCT继在生物组织检测，如眼科[2]、牙齿[3]、肠胃[4]方面取得较大优势后，在工业检测上面也发挥了它独特的作用，如应用在药物的外包[5]、纤维复合材料[6]、电子印刷、薄片检查[7]及艺术品保护[8]等一些特殊用途上。

当前，对光学相干层析系统的研究主要集中在两个方面：① 在硬件设备方面的提升，如采用宽带低相干的光源，改进系统结构，提高探测器的信噪比，采用更高精度的扫描设备降低扫描噪声等；② 成像信号进行软件处理，采用数字信号处理方法对所得图像进行增强和降噪。由于散斑噪声等不可避免的系统噪声并不能单纯通过系统硬件的提升来完全改善，同时系统硬件的提高将会较大程度上影响系统的成本，所以对OCT图像处理方法的研究技术也是当前研究的另一大热点。

1 OCT系统噪声分析

光学相干层析系统在成像时，通过将探测器检测到的图像光强电信号转换成对应像素点的灰度值，重构样品的图像信息。OCT系统在采集和传输图像的过程中，各种干扰，光源、检测电路、扫描电路等都会带来噪声，采集到的电流信号将会产生扰动，主要表现为图像中出现斑点、纹状噪声等情况，使图像分辨率下降，清晰度变差[9]。这些噪声主要包括：散斑噪声、条纹状的扫描噪声、光源噪声以及电路噪声等。

（1）散斑，也称斑纹，激光在粗糙表面反射或激光通过不均匀媒质容易产生散斑。光照射到散射颗粒后以散射颗粒为中心形成球面波散射出去，不同的颗粒散射的单次散射光可以相干叠加，产生强度随机分布的散斑图样——颗粒状[10]。

OCT的散斑噪声可以视为乘性噪声[11]，表示为：

其中：s(t)、I1(t)各表示无噪声干扰下的光学相干层析信号和含有散斑噪声的OCT信号；nsp(t)表示乘性的散斑噪声。

OCT成像时散斑现象是不可避免的，散斑和信号是共存在所获取的OCT图像中，使得图像的清晰度降低，影响研究人员对图像有用信息的提取。

（2）扫描噪声。光学相干层析系统的核心是一个迈克尔逊干涉仪，通过参考臂扫描过程中和样品臂不同深度的信息相匹配，形成每个截面的图像信息。由于多谱勒效应，信号被调制到中心频率f0处，多谱勒频移为fD=2v/λ。在OCT中，参考臂大多采用机械式扫描，若扫描速度不均匀，就会引起多谱勒频移改变，信号频带中心频率偏移，图像信号受到干扰，图像出现噪声。图像的列中突然变亮或变暗，在行上表现出条纹状亮线或暗线[12]。扫描噪声的产生与OCT的系统结构相关，通过对系统进行精密调整，保证参考光程的线性变化，就可以最大限度减少甚至消除噪声。

（3）光源噪声及电路噪声等。由于光源器件的旁瓣效应，以及电路在进行信号探测时，也会出现自激振荡，此外，光电检测器本身存在的非线性以及电阻的热噪音等都会使电路的输出信号发生改变，进而降低图像的清晰度。

综上，综合散斑噪声，扫描噪声，以及其他加性噪声na(t)的影响，实际系统采集到的OCT信号是有效信息以及各种噪声的叠加。

2 基于小波变换的OCT图像降噪

光学相干层析图像降噪处理中经常使用的方法有：高斯滤波、 中值滤波、卷积算法、自适应滤波、Wiener滤波等算法[13]。但这些算法在处理时，大多未考虑图像形状特征，在降噪的同时也模糊甚至破坏了图像的特征[14]。

与传统的降噪方法相比，小波变换在时间域和频域同时具有良好的局部化性质，而且时窗和频窗的宽度可以调节，对高频成分采用逐渐精细的时域或空域取样步长，从而可以聚焦到对象的任意细节。通过小波变换可以更容易地分离出噪声或其他不需要的信息[15]，故小波分析因其多分辨率分析的特点广泛适用于非平稳信号的处理。

国内已有学者尝试使用不同小波变换方法对所采集到的OCT图像进行消噪处理，包括：使用一维小波变换对时域信号进行解调[16]，采用软阈值方法进行多分辨率的分解重构[10]；采用双数复小波方法提取小波系数后，结合混合概率模型处理信号[17]；采用改进的双变量收缩小波进行去噪[18]；以及笔者此前采用三层平稳小波变换对OCT图像进行分解并重构[19]。这些方法均使得所得的光学相干层析图像质量得到提高，研究人员所关心的图像特性有了更好的描述。

本次研究采用连续小波变换、离散小波变换以及平稳小波变换在不同阈值的情况下对光学相干层析的处理效果进行了综合对比，得出了较优的图像处理方法。

首先，连续小波变换的结果可以表示为a和b的函数。

其中参数a和b都是连续变化的参数，a为尺度参数（在某种意义上就是频率的概念），b是时间参数或平移参数。Wf(a,b)指的是对信号f (t)进行小波变换后当频率为a，时间为b时的变换值。可以看出，一维信号f (t)经过小波变换后将变成二维信号。

离散小波变换在处理时，对尺度参数按幂级数进行离散化处理。为了减小小波变换系数的冗余度，将小波基函数限定在一些离散的点上取值，即令a=a0m，对b均匀离散，考虑到不同尺度下频率不同，因此不同尺度下参数b的离散间隔不同。

在平稳小波变换中，常用的软阈值函数，是为了解决硬阈值函数“一刀切”导致的影响。由于平稳小波硬阈值函数是当小波系数的绝对值小于给定阈值时，令其为0，大于阈值时，则令其保持不变，即将模小于3 sigma（小波系数对应的方差为sigma）的小波系数全部切除，而大于3 sigma全部保留。这样的处理方式势必会在小波域产生突变，导致降噪后结果产生局部的抖动，光谱曲线在某些点（阈值点）将产生间断（图1a）。软阈值函数在此基础上进行了改进，当小波系数的绝对值小于给定的阈值时，令其为0，大于阈值时令其都减去阈值，即将模小于3 sigma的小波系数全部置零，而将模大于3 sigma的做特殊化处理，大于3 sigma的小波系数统一减去3 sigma，小于-3 sigma的小波系数统一加3 sigma。经过软阈值函数的作用，小波系数在小波域就比较光滑，因此用软阈值降噪得到的图象看起来很平滑（图1b）。虽然小波软阈值法克服了间断缺陷，但却给重构信号引入了附加振荡，易产生恒定偏差的缺陷。由于小波软阈值法保留了部分低于阈值的高频信号，故利用软阈值可去除散斑和边峰效应[10]。

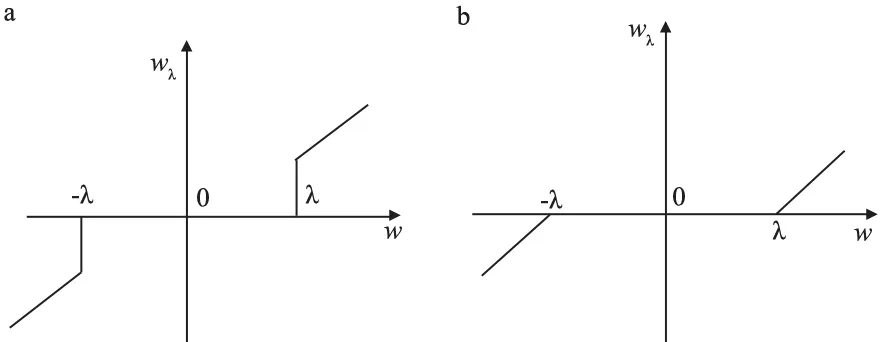
图1 硬（a）、软（b）阈值降噪函数图像

考虑利用平稳小波变换的方法，结合软硬阈值滤波方法进行改进，以得到对图像更好的去噪效果。文献已有的改进函数有两种，自行改进的函数有4种（阈值以t表示）：

（1）一种半软阈值函数，它是对软阈值函数和硬阈值函数的改进。引入参数t0=2t，在小波系数的绝对值大于等于阈值t时，保持不变；当小波系数绝对值小于t0时，取0。小波系数在此之间时，令其系数

（2）与之相似的有另外一种小波折中阈值方法，是采用参数a对原阈值函数表达式进行改进，来克服软、硬阈值法的不足。该函数表达式如下，取参数a=0.1，在小波系数的绝对值小于给定阈值时，令其为0；大于等于给定阈值时，令其为sgn(x)f (｜x｜-at)，0≤a≤1。在引入参数a后，就使得量化结果处于软、硬阈值量化之间，让重构后信号更接近原信号。

（3）继续对软阈值函数进行改进得到小波改进软阈值函数，选取参数k，令k=1，系数阈值的绝对值大等于t时，处理后的小波系数为；系数阈值的绝对值小于t时，令系数等于

（4）平稳小波新阈值函数，选取参数当小波系数的绝对值≥t时，改进后的小波系数等于；否则 令小波系数等于0。

（5）平稳小波改进阈值函数一是对半软阈值和折中阈值函数的综合改进。取a=0.1，t0=0.4t，当阈值的绝对值≥t时，改进为sgn(x)f (｜x｜-at)，0≤a≤1；当阈值绝对值大于等于t0且小于t时，改进为；其余情况下，令其为0。

（6）平稳小波改进阈值函数二是新阈值函数和改进软阈值函数的综合改进。取，当系数的阈值绝对值大于等于给定阈值t时，系数改为当阈值的绝对值小于给定阈值t时，系数改进为

3 实验验证和讨论

运用自行搭建的光学相干层析系统，检测小鼠的眼球信号，得到层析图像。受试小鼠为两个月龄的健康眼球，所用的OCT系统是自由空间的频域光学相干层析系统，系统的示意图，见图2。

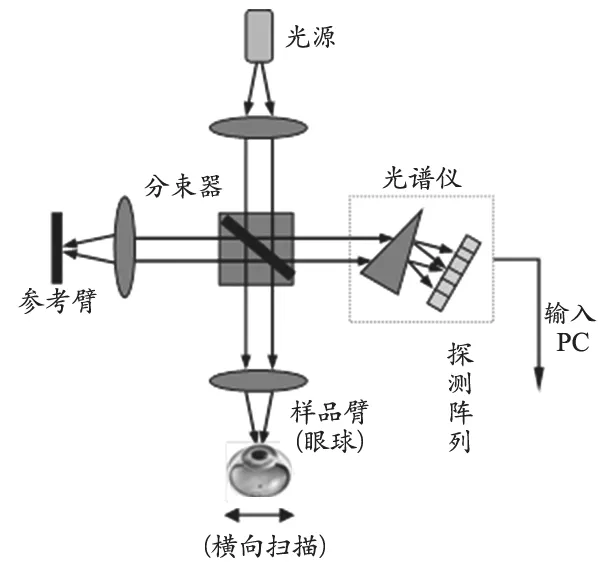
图2 自行搭建的自由空间频域OCT系统

光源采用瑞士Exalos公司的SLD超辐射发光二极管宽带光源，其中心波长为850 nm，半峰值带宽范围为105 nm，输出功率为5 mW，对应空气中的相干长度为4 μm。探测器模块采用CCD相机模块，其采集到的原始图像，见图3a，对图像分别进行连续小波变换，离散小波变换，以及采用不同的阈值来进行平稳小波变换。

在原始图像的基础上，对信号添加高斯白噪声，图像上的噪点增大，眼球信号被掩盖，方便后续更清晰地了解各算法的处理效果（图3b）；对图像进行连续小波变换和离散小波变换处理后的图像，见图3c和图3d。小波窗函数相当于一个滤波器，可分离信号的高频和低频信号，在小波分析中经常用到近似和细节，近似表示信号的高尺度，即低频信息；细节表示信号的低尺度，即高频信息。对含有噪声的信号，噪声分量的主要能量集中在小波解的细节分量中。离散小波变换减少了连续小波变换的冗余度，时域和变换域都是离散有限长的，方便计算机处理。但从图3c中可以看到，连续小波变换后，图像边缘变得模糊，信号的细节信息在处理中存在部分丢失。图3d是离散小波变换的处理后的结果，噪声信息没有明显减弱，效果并不理想。

为了更好地提高图像重构质量，进一步分析了小波降噪的分解过程。原始信号f(t)经过小波变换，图像信号按不同的频带分解，得到各尺度系数（图4）。根据文章提出的不同的阈值处理函数，得到经过阈值降噪处理后小波系数的估计值，最后运用小波逆变换进行信号重构，得到降噪后的信号。其中，小波基和分解层数的选择，阈值的选取规则，和阈值函数的设计，直接影响降噪的质量。

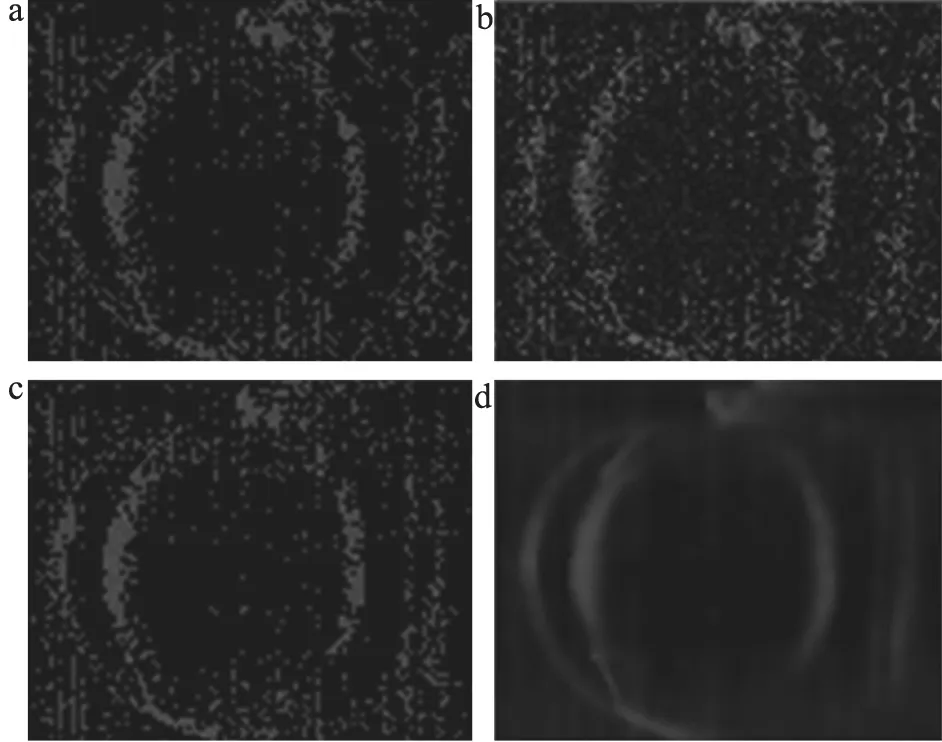
图3 原始图像及简单图像处理后效果

图4 信号的小波分解过程

本研究对小波阈值进行改进，采用多个平稳小波改进阈值函数对图像进行降噪处理，得到的效果，见图5。首先分别采用平稳小波硬阈值软阈值、半软阈值以及折中阈值方法对图像进行处理。从图5b中可得，相比与5a中硬阈值函数的处理结果，软阈值函数可以在去除图像噪点的同时，较好地识别图像的边界。从图5c半软阈值函数和图5d折中阈值函数中，可识别出小鼠眼球的角膜、晶状体、虹膜，以及视网膜结构。而原图中，并不能观察到小鼠眼睛的虹膜结构，故图像的重构质量得到较大程度的提高。从图也可知采用平稳小波变换对图像进行降噪重构的效果大大优于连续小波变换和离散小波变换。

对平稳小波的阈值进行进一步的改进，综合小波软阈值与硬阈值函数，对平稳小波变换的阈值进行优化，提出4种新的阈值函数，图像处理结果，见图6。由图可得，4种方法均提高了图像质量，可以分辨小鼠眼球的所有结构。从直观上来观察，图像上的结构信息特征相对噪声信息变得更加显著。

为了避免人眼在视觉上的偏差造成误判，在图像处理完成后，计算图像像素点灰度值的以下4个指标，以此来科学地评价处理前后的图像质量。

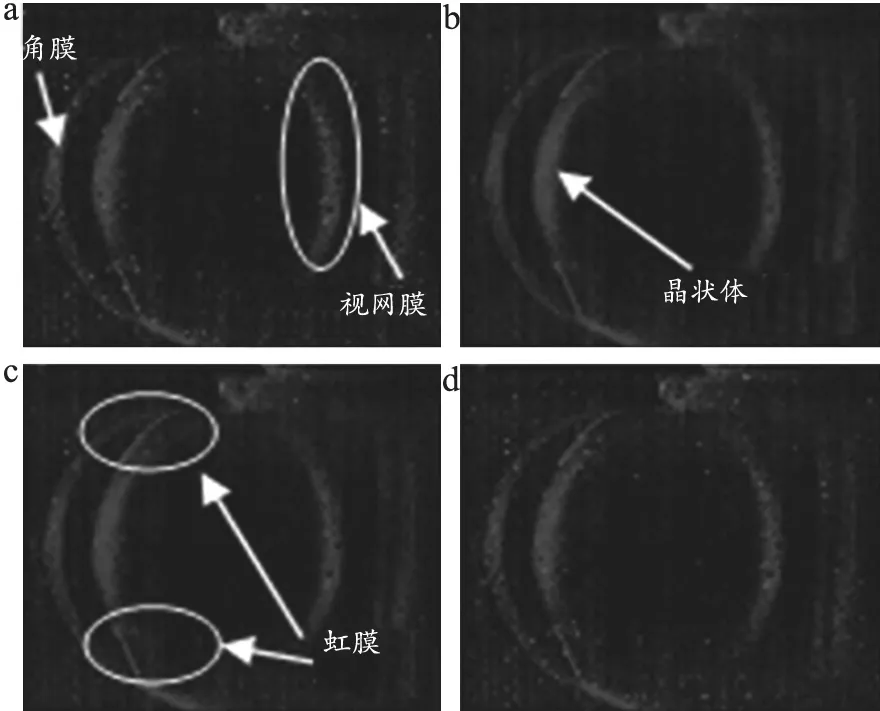
图5 四种平稳小波简单阈值函数重构图像

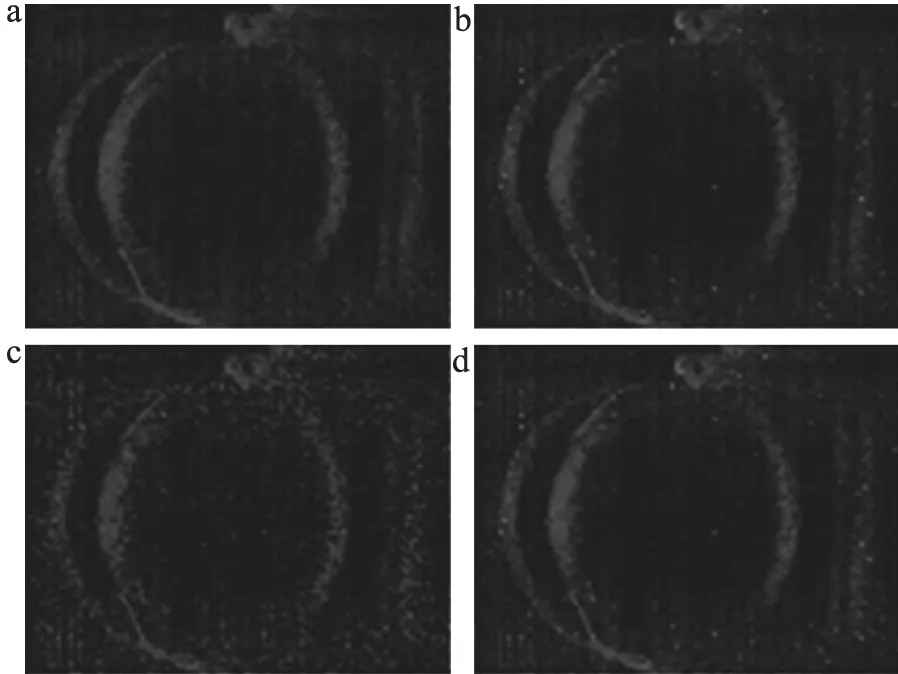
图6 四种平稳小波改进阈值函数重构图像

均方误差（MSE）：可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。

均方根误差（RMSE）：表示数据离散程度，越小说明离散程度越低。

峰值信噪比（PSNR）：反应原图像与处理图像的失真程度，PSNR值越大，就代表失真越少。

信噪比（SNR）：表征信号中有用信号与噪声的比例，其数值越高，噪音越小[15]。

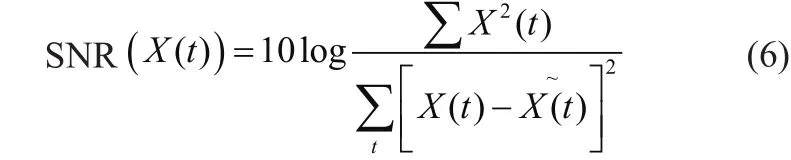
在Matlab中分析得到图像的评价结果，见表1～2。表1列举了不同阈值下4种现有平稳小波变换方法的噪声评价参数对比情况，表2列举了改进阈值的4种平稳小波方法的噪声评价参数对比情况。

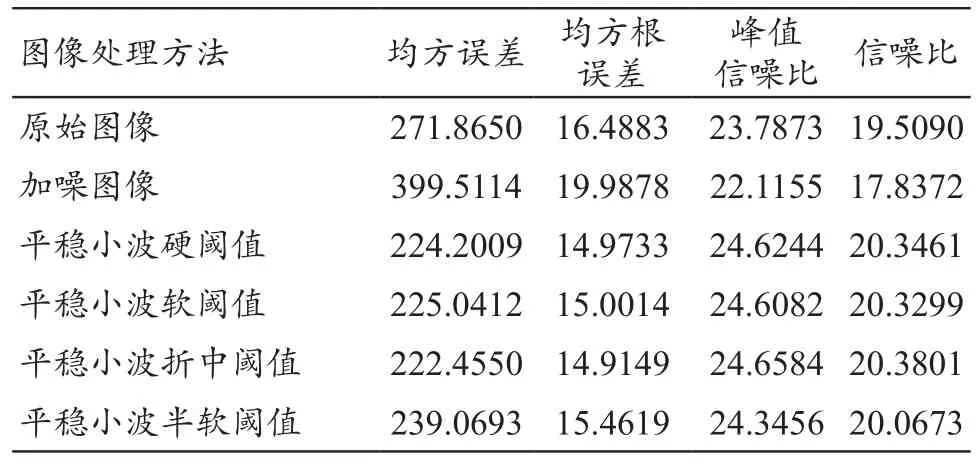
表1 不同阈值平稳小波方法的4种噪声评价参数对比

表2 改进阈值的4种平稳小波方法的噪声评价参数对比

在进行小波分解时，小波基函数的选取应兼顾紧支集、对称性、正则性、消失矩等特性。研究采用了dbN小波族，具有很好的对称性，可以减少重构时的相移。研究中，对图像进行了3层小波分解，阈值确定采用的是用“minimaxi”极大极小原理选择信号的自适应阈值。

从结果中可以得知，采用“平稳小波改进阈值函数一”进行重构的效果最好（是对半软阈值和折中阈值函数的综合改进），均方误差MSE值从加噪后的399.5114下降到了141.9361，仅为它的35.5%，并且比初始图像的271.8650也有了成倍的降低；均方根误差RMSE从加噪后的19.9878下降到了11.9137，为它的59.6%；峰值信噪比PSNR和信噪比SNR分别由加噪后的22.1155和17.8372上升到了26.6099和22.3316，升高了20.3%和25.2%，图像质量得到显著提高。

4 结论

本研究综合对比了多种小波变换方法（包括连续小波变换，离散小波变换和平稳小波变换）在小鼠眼球层析图像处理中的降噪效果。通过均方误差、均方根误差、峰值信噪比以及信噪比4个参数来定量评价不同处理方法的成像效果。研究结果表明：采用改进阈值后的平稳小波方法，图像达到的评价效果最好，该方法不仅改善了成像质量，同时也保留了图像中需要的细节信号，使得眼科光学相干层析图像的降噪性能得到提升。

[1] Huang D,Swanson EA,Lin CP,et al.Optical coherence tomography[J].Science,1991,254(5035):1178-1181.

[2] 史国华,丁志华,戴云,等.光纤型光学相干层析技术系统的眼科成像[J].中国激光,2008,35(9):1429-1431.

[3] 孟卓,姚晓天,梁燕,等.全光纤光学相干层析牙齿检测系统的解调[J].传感技术学报,2008,21(11):1858-1861.

[4] 张阳德,唐贵林,刘东非.适用于胃肠道肿瘤的内镜下新型光学成像诊断技术[J].中国内镜杂志,2001,7(3):1-4.

[5] Li C,Zeitler JA,Dong Y,et al.Non-destructive evaluation of polymer coating structures on pharmaceutical pellets using full-field optical coherence tomography.[J]. J Pharm Sci,2013,103(1):161-166.

[6] 严永福.基于DSP的光学相干层析系统研究及应用[D].福州:福州大学,2013.

[7] 秦玉伟.光学薄膜缺陷的光学相干层析检测方法研究[J].激光与光电子学进展,2015,52(7):108-111.

[8] 许鹏,何红,丁志华.光学相干层析应用于玉石亚表面结构的研究[J].中国激光,2011,38(5):210-214.

[9] 张浩楠,薛俭雷,殷玉莹,等.光学相干层析成像的图像失真及处理技术研究[J].齐齐哈尔医学院学报,2014(12):1802-1803.

[10] 刘新文,王惠南,钱志余.小波变换对OCT图像的降噪处理[J].光子学报,2006,35(6):935-939.

[11] 张仙玲,高万荣,卞海溢,等.基于经验模式分解法的光学相干层析成像降噪研究[J].光电子·激光,2012(3):602-608.

[12] 王莹利.光学相干层析术的信号与图像处理方法的研究[D].天津:南开大学,2010.

[13] Zhong S,Shen H,Shen Y.Real-time monitoring of structural vibration using spectral-domain optical coherence tomography[J]. Opt Laser Eng,2011,49(1):127-131.

[14] Zhang K,Huang Y,Kang JU.Full-range Fourier domain optical coherence tomography imaging probe with a magnetic-driven resonant fiber cantilever[J].Opt Eng,2011,50(11):119002.

[15] 吴育东,钟舜聪,沈耀春.基于SWT和ANN的无创连续血压测量方法研究[J].中国医疗设备,2017,32(5):22-27.

[16] 张雨东,戴云,史国华,等.一维小波变换在时域光学相干层析成像中的应用[J].中国激光,2008,35(7):1013-1016.

[17] 舒鹏,孙延奎,田小林.采用双树复小波和混合概率模型的光学相干层析图像去噪[J].应用科学学报,2011,29(5):467-472.

[18] 邓菊香,梁艳梅.光学相干层析图像的小波去噪方法研究[J].光学学报,2009,29(8):2138-2141.

[19] 罗曼婷,游腾飞,张秋坤,等.基于平稳小波变换的时域光学相干层析系统[J].应用光学,2015,36(4):543-549.