基于椭圆形度量谱特征的图像匹配算法
鲍文霞 余国芬 朱 明 梁 栋
(1安徽大学计算智能与信号处理教育部重点实验室,合肥 230039 )(2中国人民解放军陆军军官学院偏振光成像探测技术安徽省重点实验室,合肥 230031)
图像匹配是计算机视觉中的一个关键问题,在图像分类与检索、运动分析、立体视觉和三维重建等领域有着重要的应用.近年来,谱图理论作为一种高效的数学描述工具被广泛应用于图像匹配问题中[1-4].Leordeanu等[5]根据欧式度量构造特征点集的亲近矩阵,并对亲近矩阵进行谱分解,通过计算主特征向量之间的相似性来获得匹配关系;在此基础上,Yuan等[6]提出了权重投票策略,从而提高了谱特征匹配速度;Tang等[7]根据特征点之间的欧式距离关系,构造谱上下文结构描述符,然后定义近似距离序,将匹配问题转化为优化问题,该算法对特征点位置抖动具有一定的鲁棒性;朱明等[8]基于特征点邻域的灰度信息构造线图,并定义其邻接矩阵,通过对邻接矩阵进行谱分解获得谱特征,利用匈牙利算法求解匹配关系,提高了特征点集大小不同时的匹配精度;Yan等[9]根据特征点邻域点构造有向图的无符号Laplace矩阵,并对矩阵进行谱分解以获得谱特征,将谱特征、谱隙向量和非抽样Contourlet变换相结合,得到单调强度不变描述子,由于图及其邻接矩阵是基于邻域强度值的相对关系建立的,因此得到的单调强度不变描述子对亮度变化具有鲁棒性.
上述基于谱特征的图像匹配算法在构造谱特征及度量谱特征相似性时采用的都是欧式度量,但欧式度量将输入的样本空间看成是各向同性的,这种假设在实际应用中并不成立,不能公平反映数据样本维度分量之间的潜在关系.因此,研究者们在图像匹配问题中采用考虑样本维度分量间相关性的马氏度量代替欧式度量.例如,Bo等[10]为了克服传统图变换匹配算法中存在的问题,提出了一种基于马氏度量的加权图变换匹配算法,对特征点构造K近邻接图,利用马氏度量的中位数以及特征点与K近邻点之间的夹角距离来计算权重矩阵,从而获得匹配点对;Famouri等[11]在匹配点对上进行马氏度量学习,得到几何特性的分布,剔除其中的错误匹配,从而提高匹配精度.
采用马氏度量的匹配算法虽然提高了匹配精度,但马氏度量线性变换的局限性导致其不能描述样本潜在的非线性关系,限制其实际应用范围.为了拓宽基于谱特征的图像匹配算法的应用范围,引入对样本数据具有更好区分性的椭圆形几何,它具有能够反映样本空间结构信息或语义信息的分式线性变换;根据数据统计特性定义了椭圆形度量;利用椭圆形距离度量特征点之间的局部关系,获取特征点的椭圆形度量谱特征;根据谱特征之间的相似性构造匹配矩阵,利用贪心算法求解匹配结果.
1 椭圆形度量
1.1 椭圆形几何
给出一个半正定对称矩阵G∈R(n+1)×(n+1),由该矩阵诱导出的特征向量x,y∈Rn的双线性形式[12]为
(1)
式中,(xT,1)表示特征x的齐次坐标;G为半正定矩阵.令En={x∈Rn:σxx>0},定义ρ为
(2)
式中,k为与G相关的常数.
在En上,ρ满足度量公理,即同时满足如下4个条件:① 非负性,即ρ(x,y)≥0;② 同一性,即ρ(x,y)=0⟺x=y;③ 对称性,即ρ(x,y)⟺ρ(y,x);④ 三角不等式,即ρ(x,z)≤ρ(x,y)+ρ(y,z).因此,ρ为En上的度量.将(En,ρ)称为椭圆形几何,1/k为椭圆几何空间的曲率.
1.2 椭圆形度量矩阵
给定一个半正定对称矩阵G便可确定一个椭圆形度量ρG,此时称G为椭圆形度量矩阵.
对于给定数据集X,其均值向量及协方差矩阵的广义逆分别记为u和C.为了反映样本空间结构信息,根据数据集的统计特征,定义椭圆形度量矩阵G为
(3)
式中,常数b的取值应使G为半正定矩阵.
数据集中任意2个样本点x和y的椭圆形距离度量公式为
(4)
式中
(5)
式中,∀x∈X,有σxx>0.
已知x和y之间的马氏距离为
(6)
由式(4)可得
(7)
根据Euler公式可得
(8)
式中
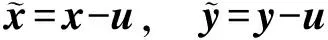
由此可得
(9)

在椭圆形度量中,1/b为椭圆形几何空间的曲率.而马氏度量几何是平坦的,其曲率为0.因此,当b→∞时,椭圆形几何的曲率趋于0,即马氏度量为椭圆形度量的极限形式.
2 椭圆形度量谱特征
假设I和J为2幅待匹配的图像.图像I中有s个特征点,记为点集P={u1,u2,…,us};图像J中有s′个特征点,记为点集Q={v1,v2,…,vs′}.图像中任意一个特征点的特征属性可以用该点与其邻近特征点之间的相互关系来描述.下面以特征点集P中的特征点ui为例,给出椭圆形度量谱特征的构造过程.
首先计算点集的平均最小椭圆形距离du为
(10)
式中,椭圆形度量矩阵GP由对应点集P计算得到.
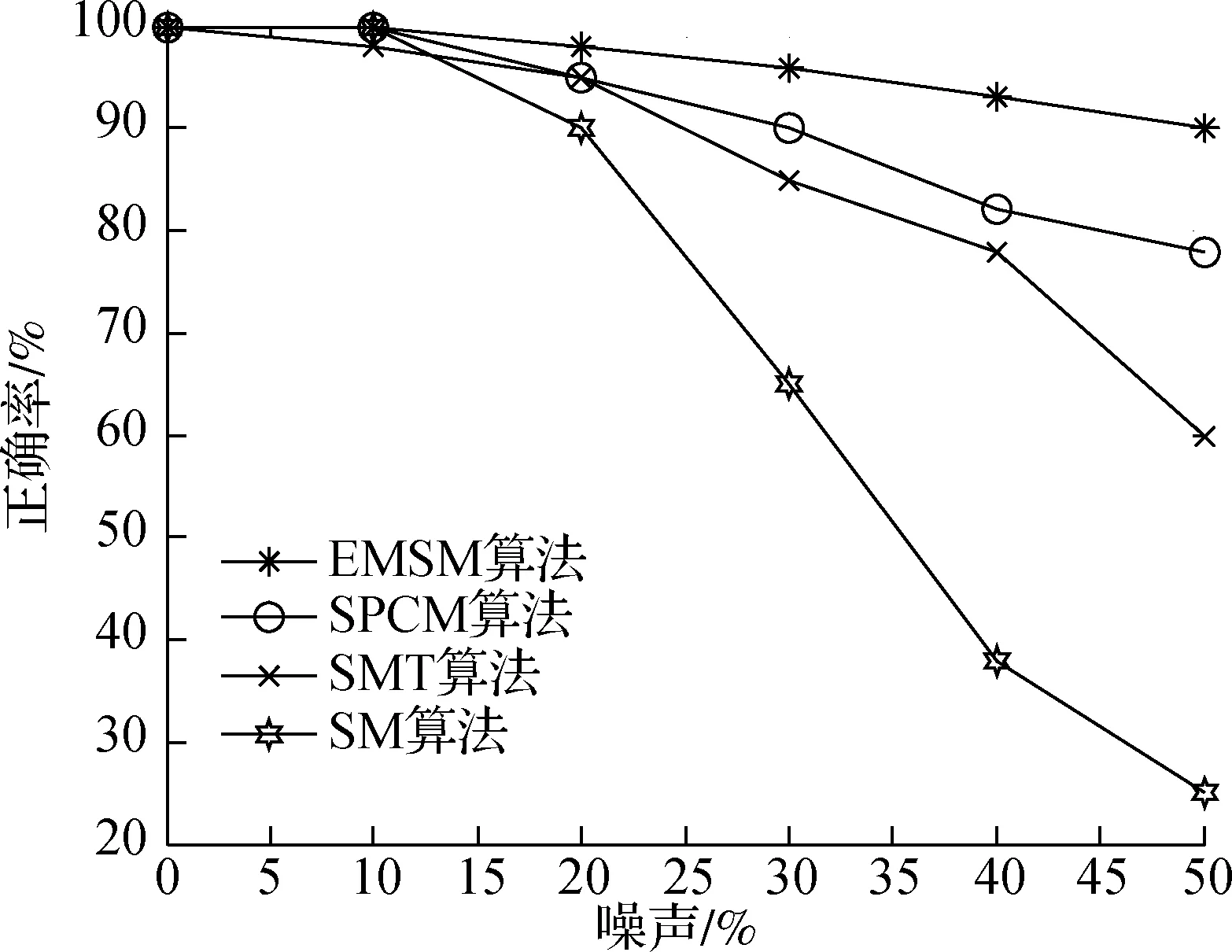
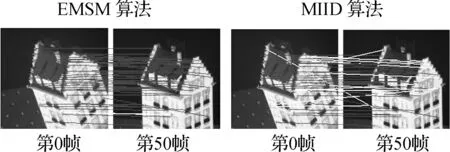
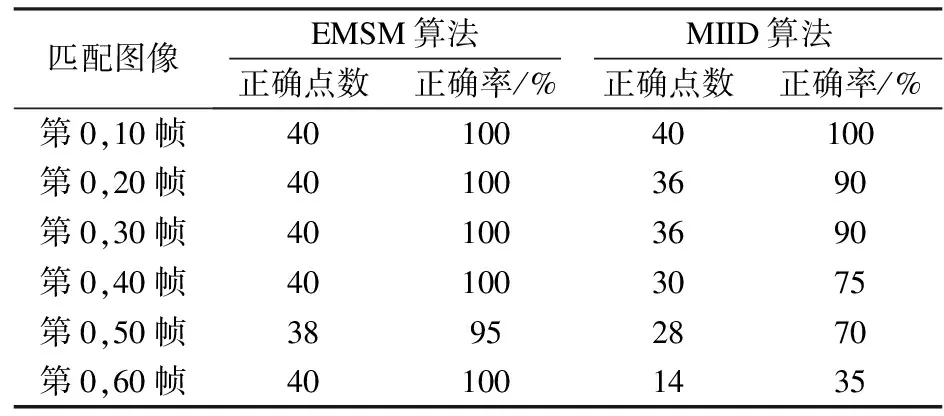
定义半径集Ru={rα|rα=αdu,α=1,2,…,5}.对于任意rα∈Ru,在点集P上选择与特征点ui的椭圆形距离小于rα的特征点,构成ui的一个子特征点集Ωiα,即Ωiα={ul:ul∈P且ρGP(ui,ul) 其次,对子特征点集Ωiα构造无向加权图,并根据椭圆形度量计算其关联矩阵为 (11) 式中,β为常数因子,用于控制特征点之间的相互作用. 然后,对关联矩阵Hiα进行谱分解可得 (12) 为了避免不等长向量之间的比较,基于特征值向量和谱隙向量的统计量来获得定长的谱特征描述.计算Aiα的最大值Fm(Aiα)、平均值Fa(Aiα)和方差Fv(Aiα),计算公式为 (13) 特征点ui的椭圆形度量谱特征可用一个特征向量来表示,即 设特征点集P中特征点ui和特征点集Q中特征点vj的椭圆形度量谱特征向量分别为Ai和Bj,则匹配矩阵M的非对角元素Mij,ij定义为Ai,Bj之间的相似性,可由椭圆形度量计算得到,即 (14) 匹配矩阵M的非对角元素Mij,i′j′定义为特征点之间的几何距离,即 (15) 式中,pii′,qjj′分别表示点集P,Q中任意2个特征点之间的椭圆形距离,即pii′=ρGP(ui,ui′),qjj′=ρGQ(vj,vj′),其中,ρGP,ρGQ为特征点之间的椭圆形距离,GP,GQ为点集P,Q的椭圆形度量矩阵;ρG″为pii′,qjj′之间的椭圆形距离,其中G″为特征点集P和Q构成的数据集的椭圆形度量矩阵. 根据构造的匹配矩阵M,采用通用的匹配数学模型[13-14],可将特征匹配问题描述为 (16) 式中,w为二进制分配矩阵W的列向量形式.当图像I中特征点ui和图像J中特征点vj匹配时,Wij为单位矩阵,否则Wij为零矩阵. 求解匹配问题转换为求分配向量w*使式(16)中的目标函数最大化.采用贪心算法[5]求解该匹配数学模型,得到匹配结果. 基于椭圆形度量谱特征的图像匹配算法流程如下: ① 在待匹配图像的特征点集中分别计算椭圆形度量矩阵; ② 为每个特征点构造椭圆形度量谱特征; ③ 利用椭圆形度量谱特征之间的相似性以及特征点之间的几何距离计算匹配矩阵; ④ 根据通用的匹配数学模型,采用贪心算法求解匹配关系. 为了验证基于椭圆形度量谱特征的图像匹配算法(EMSM算法)的性能,分别对模拟数据和真实图像进行了实验. 首先,生成模拟数据点集P和Q.点集P由二维平面内服从高斯分布N(0,1)的随机点集构成,共计40个点.点集Q由点集P中的点经过旋转和平移变换并叠加一定的高斯噪声得到,其中旋转和平移变换的参数为一定范围内的随机值,旋转角度θ∈[-π,π],在x轴和y轴上的平移量t∈[-1,1],高斯噪声的均值为0,方差为点集中最近距离平均值的倍数.然后,分别采用EMSM算法、SPCM算法[7]、SMT算法[2]以及SM算法[5]在模拟数据上进行100次独立实验,将匹配正确率的平均值作为实验结果(见图1).由图可知,噪声改变时,EMSM算法仍然能够保持较高的匹配精度,SM算法则受噪声影响最严重.EMSM算法对噪声具有较高的鲁棒性,究其原因在于引入了对数据具有更好区分性的椭圆形度量来构造谱特征. 图1 4种算法正确率随噪声变化曲线图 为验证椭圆形度量谱特征的性能,采用CMU/VASC图像数据库中的序列图像进行实验.以hotel图像序列中第0,10,20,30,40,50,60帧为例,在每帧图像上提取40个特征点,分别用EMSM算法和MIID算法[9]对特征点构造谱特征,然后采用相同的匹配数学模型以及贪心算法将其余帧分别与第0帧进行匹配,实验结果见图2和表1.从实验数据分析可得,EMSM算法较MIID算法具有更高的匹配精度,第60帧时仍然能够达到100%的正确匹配率;仅第0和50帧的匹配精度没有达到100%,这是因为其中2个特征点的位置基本重叠. (a) 第0,10帧图像匹配 (b) 第0,30帧图像匹配 (c) 第0,50帧图像匹配 (d) 第0,60帧图像匹配图2 4种算法在hotel图像上的匹配实验结果 表1 hotel图像匹配实验数据 其次,为了验证基于椭圆形度量谱特征的图像匹配算法的应用范围,利用graffiti6图像集中视角变化较大的2幅图像进行匹配算法对比实验.在每幅图像中提取40个特征点,分别利用EMSM算法、SPCM算法[7]、SMT算法[2]以及SM算法[5]进行匹配,实验结果见图3和表2.从实验数据分析可得,EMSM算法在视角变化较大情况下正确匹配率仍然保持100%.因此,EMSM算法对视角变化具有不变性. (a) EMSM算法 (b) SPCM算法 (c) SMT算法 (d) SM算法图3 4种算法在graffiti6图像上的匹配实验结果 表2 graffiti6图像匹配实验数据 然后,采用具有较大形变的2幅Boat图像进行匹配实验.在每幅图像中提取40个特征点,分别用EMSM算法、SPCM算法[7]、SMT算法[2]以及SM算法[5]进行匹配,结果见图4和表3.从实验数据分析可得,EMSM算法匹配精度为100%,SPCM算法匹配精度次之,SMT算法的匹配精度仅为50%,SM算法的匹配精度最低.由此可知,EMSM算法对形变具有不变性. (a) EMSM算法 (b) SPCM算法 (c) SMT算法 (d) SM算法图4 4种算法在Boat图像上的匹配实验结果 表3 Boat图像匹配实验数据 定义的椭圆形度量具有能够反应特征空间结构信息或语音信息的分式线性变换,对特征具有良好的区分性,能够较为准确地对特征点之间的潜在关系进行建模.所构造的椭圆形度量谱特征根据特征点之间的相对椭圆形距离选择子特征点集,而平移和旋转变换不会改变特征点之间的相对距离,故椭圆形度量谱特征具有平移不变性、旋转不变性以及尺度不变性.因此,基于椭圆形度量谱特征的图像匹配算法在序列图像以及视角变换、形变较大图像匹配中基本上都能达到100%的匹配准确率,高于其他对比算法. 1) 针对欧式度量不能反映数据维度分量之间的潜在关系以及马氏度量不能描述样本潜在非线性关系的缺点,定义了一种椭圆形度量.该度量能够反映样本空间结构信息或语义信息. 2) 在特征描述阶段,根据特征点之间的相对椭圆形距离选择特征点子集,结合谱理论构造描述特征点属性的椭圆形度量谱特征. 3) 在特征点匹配阶段,利用椭圆形度量计算谱特征之间的相似性,从而得到匹配关系. 4) 模拟数据和图像数据实验结果表明,基于椭圆形度量谱特征的图像匹配算法提高了匹配精度,并对噪声具有较高的鲁棒性,适用于图像视角变换较大和形变较大的匹配问题. 参考文献(References) [1] Carcassoni M, Hancock E R. Spectral correspondence for point pattern matching[J].PatternRecognition, 2003,36(1): 193-204. DOI:10.1016/s0031-3203(02)00054-7. [2] Feng W, Liu Z Q, Wan L, et al. A spectral-multiplicity-tolerant approach to robust graph matching[J].PatternRecognition, 2013,46(10): 2819-2829. DOI:10.1016/j.patcog.2013.03.003. [3] Yang X, Qiao H, Liu Z Y. Feature correspondence based on directed structural model matching[J].ImageandVisionComputing, 2015,33: 57-67. DOI:10.1016/j.imavis.2014.11.001. [4] Peng X, Yu Z, Yi Z, et al. Constructing the L2-graph for robust subspace learning and subspace clustering[J].IEEETransCybern, 2017,47(4): 1053-1066. DOI:10.1109/TCYB.2016.2536752. [5] Leordeanu M, Hebert M. A spectral technique for correspondence problems using pairwise constraints [C]//TenthIEEEInternationalConferenceonComputerVision. Beijing, China, 2005: 1482-1489. DOI:10.1109/iccv.2005.20. [6] Yuan Y, Pang Y, Wang K, et al. Efficient image matching using weighted voting[J].PatternRecognitionLetters, 2012,33(4): 471-475. DOI:10.1016/j.patrec.2011.02.008. [7] Tang J, Shao L, Zhen X. Robust point pattern matching based on spectral context[J].PatternRecognition, 2014,47(3): 1469-1484. DOI:10.1016/j.patcog.2013.09.017. [8] 朱明,梁栋,范益政,等.基于谱特征的图像匹配算法 [J].华南理工大学学报(自然科学版),2015,43(9): 60-66. DOI:10.3969/j.issn.1000-565X.2015.09.010. Zhu Ming, Liang Dong, Fan Yizheng, et al. Image matching algorithm based on spectral feature [J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2015,43(9): 60-66. DOI:10.3969/j.issn.1000-565X.2015.09.010. (in Chinese) [9] Yan P, Liang D, Tang J, et al. Local feature descriptor invariant to monotonic illumination changes[J].JournalofElectronicImaging, 2016,25(1): 013023. DOI:10.1117/1.jei.25.1.013023. [10] Bo D, Zhang G L, Cui X L. An algorithm of image matching based on Mahalanobis distance and weighted KNN graph [C]//2015InternationalConferenceonInformationScienceandControlEngineering. Shanghai, China, 2015: 116-121. [11] Famouri M, Azimifar Z. A statistical approach to rank the matched image points [C]//2016 24thIranianConferenceonElectricalEngineering. Shiraz, Iran, 2016: 1214-1218. DOI:10.1109/iraniancee.2016.7585706. [12] Klein F. Ueber die sogenannte Nicht-Euklidische geometrie[J].MathematischeAnnalen, 1970,6(2): 112-145. DOI:10.1007/BF01443189. [13] Zhou F, Torre F D L. Deformable Graph Matching [C]//2013IEEEConferenceonComputerVisionandPatternRecognition. Portland, USA, 2013: 2922-2929. DOI:10.1109/cvpr.2013.376. [14] Cho M, Sun J, Duchenne O, et al. Finding matches in a Haystack: A max-pooling strategy for graph matching in the presence of outliers [C]//ComputerVisionandPatternRecognition. Columbus, OH, USA, 2014: 2091-2098.DOI:10.1109/cvpr.2014.268.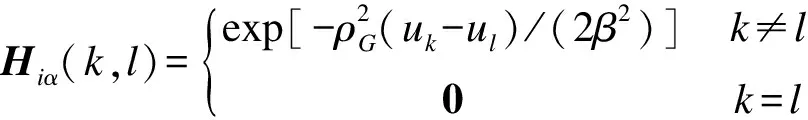
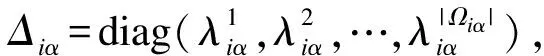

3 特征匹配
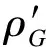
4 算法流程
5 实验结果与分析
5.1 模拟数据实验结果
5.2 真实图像匹配结果









6 结论

