基于RSSI的无源信号定位算法研究
胡 洋,田 忠,伍习光,王 平
(电子科技大学电子科学技术研究院,四川 成都 611731)
0 引言
无源信号定位是指利用单个或多个分布式的有源或无源探测工具(如频谱仪),通过接收目标反射或者发射的信号,分析数据中的信号和相关参数,并应用有效的数据处理方法估计目标在空间中的位置[1]。对于观测环境而言,它首先从接收到的待测目标信号中获取可利用的定位信息或参数,如到达时间差、方位角、俯仰角、接收信号强度、距离等。这些信息在空间中都对应着一个曲面。观测点获取的、属于同一待测目标的定位参数,它所对应的曲面称为定位面。通过对这些曲面的几何图形分析,可以得到面面相交的直线或曲线;利用直线或曲线与面或线相交,就能得到某一确定的空间区域或点,并可以确定待测目标信号的具体坐标[2]。
无源信号定位主要可以分为两种方式。一种是基于距离(Range-based)的定位算法,其在定位时需要对已知参考节点间的距离或者角度进行测量;另一种是与距离无关(Range-free)的定位算法[3-4]。Range-based的定位方法有接收信号强度指示(received signal strength indication,RSSI)测量法、基于到达时间 (time of arrival,TOA)测量法、基于到达时间差(time difference of arrival,TDOA)测量法等。目前,在基于距离的定位算法中,基于RSSI的定位算法较为简便、快捷。
本文首先介绍了RSSI的定位原理,分析了实际应用过程中定位误差产生的原因。在此基础上,利用最大似然估计(maximum likelihood estimate,MLE)优化算法,通过距离与节点信号接收强度(功率)之间的估计关系以及对节点信号最大值和最小值的排序和循环处理,减小信号反射和多径效应等因素对定位过程造成的干扰,从而减小定位误差,达到定位要求。
1 定位原理
1.1 测距原理
由电磁波传播理论可知,电磁波信号在传播过程中会产生能量损耗。这种损耗与电磁波的传播路径有关。RSSI定位测距模型正是基于这种相关性,计算出待定位信号节点到参考信号接收点之间的距离。在实际测试环境中,由于多径效应、反射以及绕射、不规则传播等因素,使得模型比较复杂,定位误差也较大[5]。因此,在多数情况下,采用对数路径损耗模型表示接收功率与距离的关系[6]:
(1)
式中:Pr(d)为参考信号接收节点在d处的接收信号强度;d0为参考距离,取值一般为1 m;Pr(d0)为参考信号接收节点在d0处的接收信号强度;n为路径衰减因子,代表传播能量的损耗随距离变化的指数,环境不同取值不同,其范围一般为2~4;Xσ为零均值、标准差为σ的正态随机变量,表示空间噪声对能量传播的影响,σ的取值范围为4~10[7]。
1.2 定位基本原理
参考信号接收节点的接收信号强度正相关于目标节点与接收节点之间的距离。也就是说,信号强度越强,表明待定位目标节点离参考信号接收节点距离越小;反之,表示待定位目标节点离参考信号接收节点距离越远。理论上,只需3个参考接收节点,就可对1个未知目标信号节点进行定位。但由于空间中存在信号衰减、障碍物的反射和吸收、空间噪声等干扰因素,为了保证较高的定位精度,一般使用4个或者更多的参考信号接收节点。定位原理如图1所示。
图1中,待定位目标节点(图中T所示)处于4个参考信号接收节点(图中R所示)的接收区域内,4个参考信号接收节点R同时接收到待定位目标节点T发射出的信号。其接收信号强度反映了待定位目标节点与各参考信号接收节点的距离。根据接收到的信号强度值或功率值,再利用路径损耗公式,就可以获得接收节点和目标节点间的距离,从而判断待定位目标节点的具体坐标信息。

图1 定位原理图Fig.1 Positioning principle diagram
2 传统基于RSSI的三边测量法
三边测量法[8-9]步骤如下。假设某一待定位目标信号节点O和三个位置已知的参考信号接收节点A、B、C。首先,通过这3个参考信号信号接收节点接收目标节点信号强度,在这里一般指信号功率。然后,由路径损耗模型间接得到待定位目标节点O与3个参考信号接收节点A、B、C之间的距离,设它们分别是d1、d2、d3。最后,分别以参考信号接收节点A、B、C为圆心,d1、d2、d3为半径作圆。3个圆的相交处就是需要确定的目标节点O。
假设待定位目标信号节点O的坐标为(x,y),参考信号接收节点A、B、C的坐标分别是(x1,y1)、(x2,y2)、(x3,y3),可得待测目标信号锚节点的坐标计算公式为:
(2)
化简式(2),即可求得目标信号节点O(x,y)的坐标表达式:

(3)
传统三边测量法在理想情况下,三圆相交于一点,可得到待定位目标节点的坐标。但在—般情况下,由于空间中某些因素和探测仪器的误差影响,待定位目标节点O与3个参考信号接收节点A、B、C之间的距离会出现误差,有可能会出现3个圆有3个交点或者无交点的情况,导致无法实现目标源定位。因此,需要其他方法来减小传统测量方法存在的定位误差。
3 基于RSSI的MLE定位优化算法
在无线传感器网络定位方法中,以RSSI为基础的定位算法较为方便、快捷。而在实际传播空间中,如建立无源信号的RSSI累计概率分布函数模型,就可以使用RSSI分布函数模型解决无源信号的位置估算问题,从而得到无源信号节点的确切坐标信息。其算法的流程如下。
(1)在(O,L)内随机产生一个数a,同时初始化数b。已知参考信号接收节点接收到的待测目标信号强度RSSI为P=(P1,P2,P3,P4)。
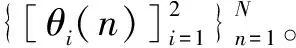
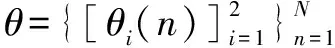
(5)当距离为r时,接收信号强度为P的条件概率:
(4)
(6)由式(4)可知,N(N=100)个随机样本点条件下,接收信号强度为P的联合概率分布为:

(5)
(7)对式(5)取对数,得:

(6)


③循环次数加1,若循环次数大于Tmax,即结束循环,返回最新的均值μ作为未知节点的位置坐标估计值;否则,利用高斯正态分布函数继续产生N(N=100)个随机样本点,然后重新开始计算其MLE值。
4 仿真试验结果及分析
在仿真场景中,部署了4个参考信号接收节点,分别位于定位范围为8 m×8 m的区域中;在该区域的4个顶点处,随机生成该区域的一个坐标未知的目标信号节点。各节点间通信正常,路径损耗因素η=4。所有仿真试验环境中都加入均值为0、标准差σ=4、满足高斯分布的随机噪声。
4.1 三边测量法
分别以4个参考信号接收节点为圆心、待定位目标节点与参考信号接收节点的距离为半径,得到如图2所示的三边测量法仿真图。

图2 三边测量法仿真图Fig.2 Trilateration simulation
图2中,4个圆相交的区域即为待定位目标节点的位置分布。随机生成的待定位目标信号节点(白色小圆形所示)的实际坐标值为(4.608 7,4.866 9),而运用传统三边测量法测得的待定位目标信号节点的位置坐标值(三角形所示)为(7.362 0,4.458 6)。可以得到三边法定位的位置坐标与实际位置坐标的定位误差为2.310 0。
为准确统计该算法的定位误差结果分布并分析该算法的稳定性,仿真统计了100次实际坐标值与估计坐标值的定位误差,得到三边测量法累计概率分布如图3所示。

图3 三边测量法累计概率分布图Fig.3 Cumulative probability distribution of trilateration
4.2 MLE定位优化算法
在相同条件、相同仿真环境下进行试验。本次仿真试验中,随机样本点数量N=100;最大随机样本点数量Nmax=10;随机数a∈[0,8];初始数b=10;循环次数Tmax=1 000。MLE定位优化算法所采用的参数如下。MLE定位优化算法仿真图如图4所示。

图4 MLE定位优化算法仿真图Fig.4 Simulation of MLE positioning optimization algorithm
图4中,4个已知坐标参考信号接收节点(白色正方形)在定位区域的4个顶点上,随机生成图中所示三角形(白色)位置的待定位目标信号节点,其坐标为(5.504 7,7.055 2)。然后,输入参数及参考信号接收节点信息至MLE定位优化算法,计算出的待定位未知信号节点(黑色三角形)的位置坐标为(5.930 1,6.2141)。由此可知,优化算法得到的未知信号节点的位置坐标结果与实际位置坐标结果的误差距离为0.901 8,误差远小于三边测量算法。由此证明,该算法有效提高了定位精度。
MLE定位优化算法的定位误差累积概率(cumulative distribution function,CDF)曲线如图5所示。由图5可以看出,定位误差主要在1~4 m范围内,且误差分布比传统三边法分布更均匀。所以MLE定位优化算法在稳定度上比三边测量算法更好。MLE定位优化算法平均定位误差小于2.5,比三边测量算法性能更优。通过比较三边测量算法和MLE定位优化算法的CDF曲线可知,MLE定位优化算法的曲线更加平滑,而且MLE定位优化算法的定位精度更高,所以定位结果更加符合实际值。因此,与传统定位方法相比,MLE定位优化算法更适用于定位;在实际测量中,定位结果更符合要求,而且具有良好的稳定性。
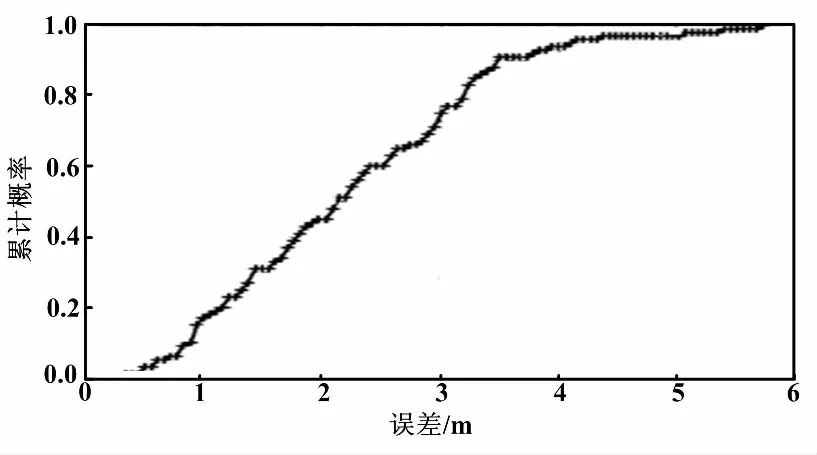
图5 定位误差累积概率曲线Fig.5 CDF curve of positioning errors
5 结束语
本文在研究了路径损耗模型和传统RSSI三边定位算法的基础上,提出了MLE定位优化算法。该算法通过建立无源信号在实际空间环境中发射时,接收信号功率RSSI的累计概率分布函数模型,以进行未知信号源的坐标信息估计。本文通过仿真测试,总结了大量的结果数据,得到了对应的定位误差累积概率曲线。由此更清晰地表明,MLE定位优化算法减小了定位误差。通过仿真,比较了本文算法和传统定位算法在稳定性和定位精度上的优劣。由对比结果可知,MLE定位优化算法不仅稳定性更好,而且有效地提高了定位精度,在无源信号定位中有着广阔的应用前景。
参考文献:
[1] 吴林晟.遗传算法及其在无源测向定位中的应用[D].上海:交通大学,2006.
[2] 高为.无源定位技术研究[D].上海:上海交通大学,2006.
[3] 陈锡剑,程良伦.基于 RSSI 的功率匹配定位算法的研究与实现[J].传感技术学报,2013,26(5):710-714.
[4] 刘政.无线传感器网络节点自适应加权定位算法[J].自动化仪表,2015,36(6):1-4.
[5] 王山,冯锋,王洪伟.基于RSSI的三维空间定位算法研究[J].电脑知识与技术,2016,12(9):221-224.
[6] 钟丽鸿,胡成全,金京姬.基于RSSI极大似然估计定位算法的分析与实现[J].吉林大学学报(理学版),2014,52(3):556-560.
[7] 瞿玉玲.基于RSSI的无源信号定位算法研究[D].南京:南京邮电大学,2015.
[8] 高晗.基于车地频谱地图的GSM-R干扰源与克隆基站定位技术[D].成都:西南交通大学,2014.
[9] 曹群瑶.GSM无线网络干扰源定位的研究[D].杭州:浙江工业大学,2013.
[10]朱骅.基于无线信号的定位算法研究与实现[D].北京:北京邮电大学,2014.

