Particle Size Influence on the effective Permeability of Composite Materials∗
Tai Xiang(向泰),Ru-Neng Zhong(钟汝能),Bin Yao(姚斌),Shao-Jing Qin(覃绍京),and Qin-Hong Zheng(郑勤红),†
1Key Laboratory of Photoelectric Information Technology,Yunnan Province&Solar Energy Research Institute,Yunnan Normal University,Kunming 650500,China
2Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China
1 Introduction
It is highly advantageous to obtain theoretical predictions for the electromagnetic parameters of materials,to establish the general dependence and relation between various microstructure and macroscopic quantities of composite materials.A theoretical estimation provides much more information than a numerical simulation data or an experimental data,and it guides material design.This work is concerned with the theoretical model of the technology and application of composite materials,especially for the effective permeability of particle dispersed system in Fig.1.
The effective electromagnetic parameters of composite materials can be obtained through assumptions and simplifications,such as Clausius-Mossotti equation,[1]Lorentz-Lorentz equation[2]and Maxwell-Garnett formula.[3−5]Many such kind of self-consistent effective medium theories have been developed.[6−10]Markel summarized two tutorials which are devoted to the Maxwell-Garnett approximation and related theories.[11−12]The effective permeability of composites has been theoretically estimated.[13−17]The effective permeability of Ce2Fe17N3−δparticles/epoxy resin composites with various volume concentrations were measured in the frequency range of(0.1–15)GHz.[18]Materials were analyzed in a finite element software(COMSOL Multiphysicsc),[19]and other numerical methods.[20]The variation approach is another kind of method to calculate the effective magnetic permeability of composite material,[21−24]and it has been implemented numerically.[25]Series expansion and several derivations have been done for materials with special structures.[26−31]Numerical method in these schemes has also been developed.[32−33]
In the meantime,the study of macroscopic electromagnetic properties of the soft magnetic composite has made much progress.[34−39]Peng et al.studied the effective electromagnetic parameters in random mixture media of magnetic iron fiber.[40]Choi et al.designed the microstructure with the prescribed magnetic permeability and proposed a design method to control the magnetic flux flow by layered microstructures.[41]Thabet et al.studied the effective permeability of new nanocomposites magnetic materials based on theoretical approaches at terahertz frequencies to exhibit weak electric and magnetic responses.[42]Barski et al. first considered the possibility of theoretical predictions of effective properties for smart materials.[43]
According to the de fi nition of the magnetic permeability,one estimation of the effective magnetic permeability is calculated from the average of the fields /
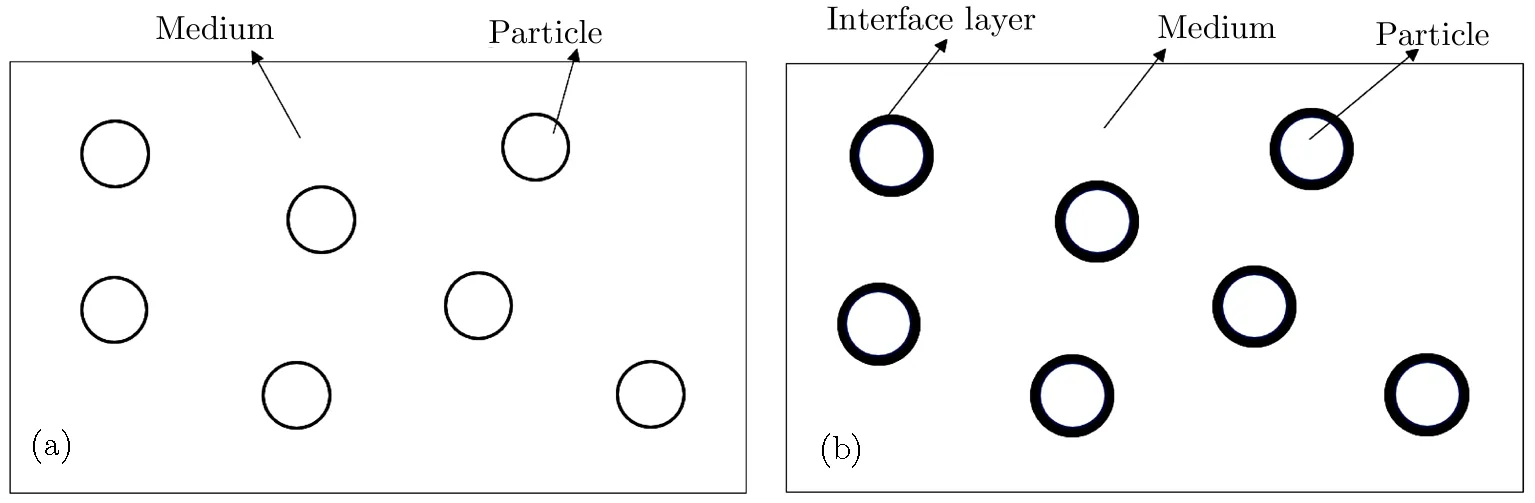
Fig.1 Model for composite material with mixed particles.(a)There is not an interface layer on the surface of a particle.(b)There is an interface layer on the surface of a particle.
Particles can be so tiny on nanometer scale,and the size of the interface to the size of the particle is big.We will study particles in nanoscale.The distance between particles is larger than the particle size.The interaction between particles is negligible.The particle radius is much smaller than the electromagnetic wavelength.With these approximations,we study in the following sections how the particle size affects the effective permeability through classical models for superconductor and normal particles,we discuss the difference between the energy method and direct field average method.
2 Mawell-Garnett Method
We derive the magnetic intensity and induction of every domain of the composite material from Maxwell equation,then calculate the effective magnetic permeability of the composite material.
Let the composite material be in a uniform static magnetic field.The static magnetic intensity is H0eZ,the volume of the composite material is V,the total volume of all particles isV1,the medium volume which excludes particles is V3.Letfbe the volume ratio of the particles.The radius of a particle is R,the number of the particles in the composite material isN.Thus,V1=f V=4Nπ R3/3 and V3=(1−f)V.The magnetic intensity in the particles and medium are H1and H3,and the magnetic induction of the particles and medium are B1and B3,respectively.The magnetic permeability of the particles and medium is µcand µm.The effective magnetic permeability of the composite material is µeff−MG.
Equation(1)is the Laplace equation of magnetic scalar potential of the static magnetic field,and its general solution is Eq.(2).an,bn,cn,dn(n=1,2,3,...)are coefficients of the general solution,which must satisfy the boundaryvalue relation and boundary condition.
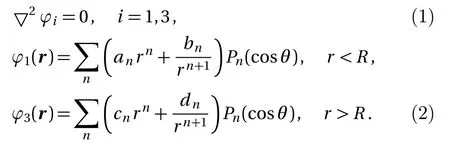
According to the asymptotic boundary condition and the boundary-value relation as Eq.(3),the coefficients of the functions in all domains can be exactly determined for this system.
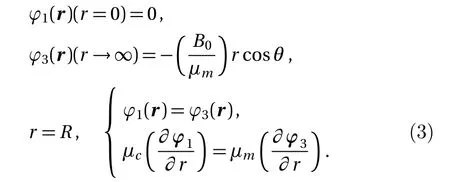
The unique solution with all nonzero coefficients can be calculated.
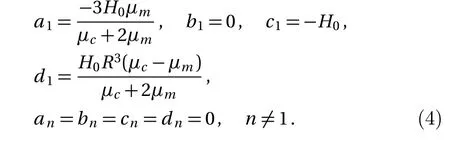
Local magnetic intensity is
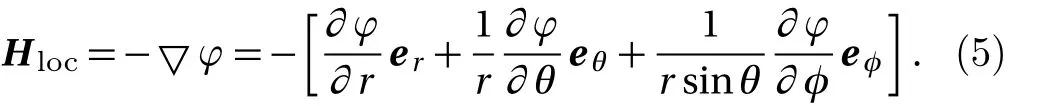
Then,we can get the magnetic intensity in the particle and medium,respectively.
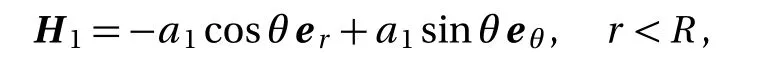
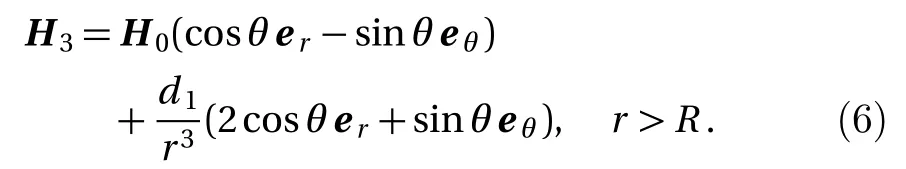
The effective magnetic permeability obtained from the volume average of the fields is

with
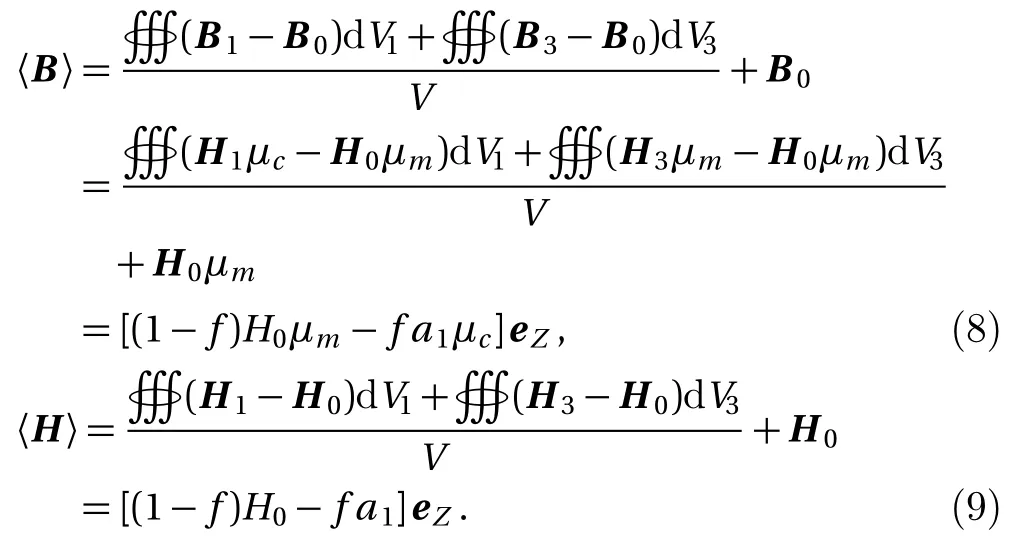
Thus,
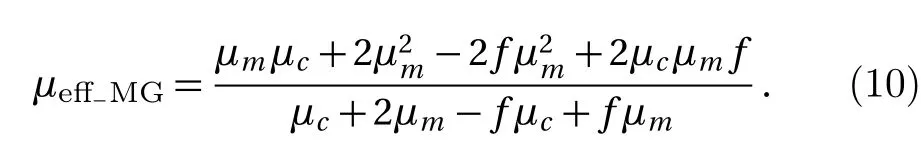
It is the Maxwell-Garnett equation.
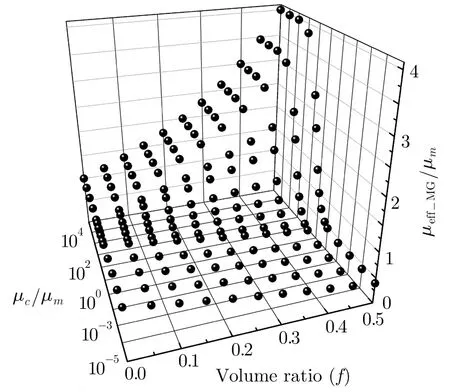
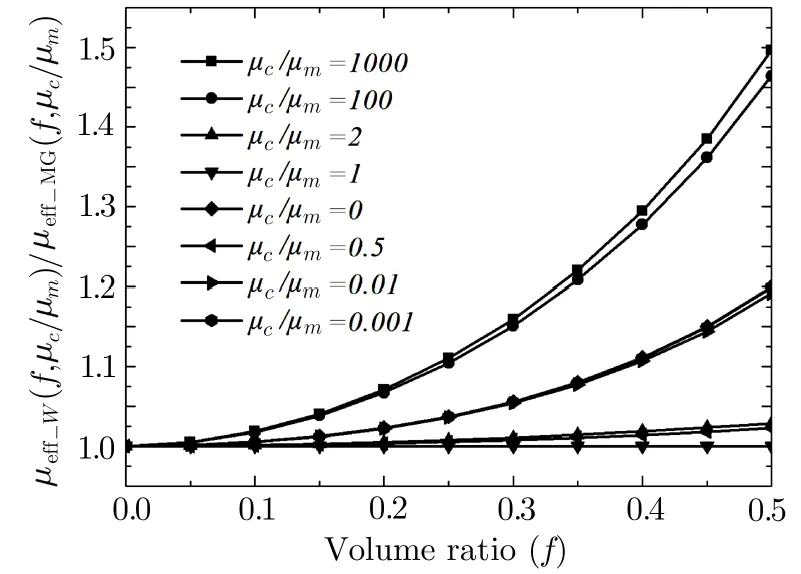
Fig.2 The effect of particle filling in Eq.(11).It is a three-dimensional scattering point map with µe ff−MG/µm vs.fand µc/µm.
The effect of the particle filling can be discussed through µeff−MG/µmplotted in Fig.2,which indicates the tendency with µeff−MG/µmvs.fand µc/µm.
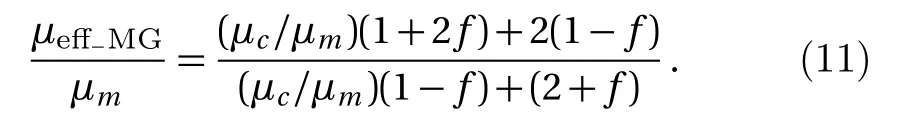
In Fig.2,the effective permeability of the composite can be increased or decreased through the change of the magnetic particle permeability and particle volume ratio.When µcis bigger than µm,the effective permeability of the composite material increases with the increase of particle volume ratio. Ifµc/µm→ ∞,andf→ 0.5,µeff−MG/µm→ 4.When µcis smaller than µm,the effective permeability of the composite material decreases with the increase of particle volume ratio.Ifµc/µm→ 0,and f→ 0.5,µeff−MG/µm→0.4.Therefore,for the reasonable filling range f<0.5,no matter how we change the properties of the particle,we always have a permeability for the composite in a finite range,0.4µm≤ µeff−MG≤4µm.
3 Energy Method
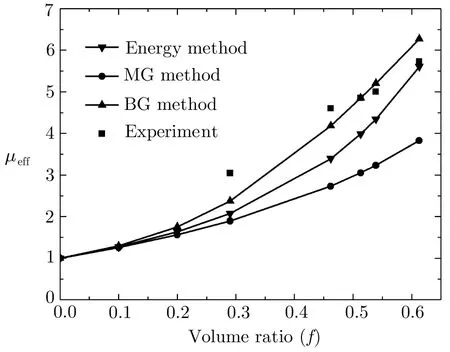
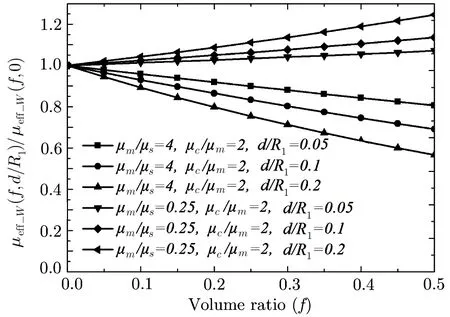
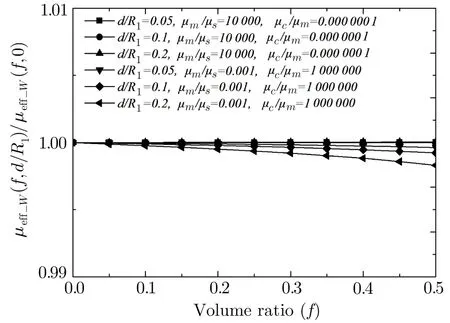
Magnetic field is a form of energy,so the process of magnetization can be analyzed through energy.The energy of the magnetic field is related to the integral of the magnetic intensity,magnetic induction and space volume of magnetic field.Let with By Eqs.(4),(6),(9),and(13),we can obtain So,the effective permeability of the composite material is Forboth Maxwell-Garnett method and energy method,the effective permeability of the composite material depends on µc,µm,andf.It does not depend on particle size R.We will reveal in next section the size dependence of the effective permeability,after we consider the thickness of the interface layer between the particle and the medium. Obviously,(1/R6)fµmin Eq.(15)is the energy,which comes from the magnetic dipole of the particle in numerator of the energy method equation.When we integrate the energy density,the integration contains the contribution of the magnetic dipole.The field contribution of the magnetic dipole is zero in the denominator in Eq.(12)of energy method,where the magnetic intensity field is averaged.When the magnetic intensity and induction are integrated in the Maxwell-Garnett formula,the average fields generated by the dipole are also zero because of the symmetry.So comes the difference between Eqs.(10)and(16),with the dipole energy effect missed in the Maxwell-Garnett formula. The effect of the magnetic particle dipole can be demonstrated by the ratio of effective permeability by energy method and the Maxwell-Garnett method,and it is plotted in Fig.3: Fig.3 The effect of the magnetic dipole of the particle in Eq.(17). µe ff−W(f,µc/µm)/µe ff−MG(f,µc/µm)vs.volume ratio fis plotted for parameters µc/µm =1000,100,2,1,0.5,0.01,0.001,0. µeff−MG(f,µc/µm)is much different from µe ff−W(f,µc/µm)when µc/µmis far from unity. When µc≪ µmand f→0.5,the effect of the magnetic dipole of the particle is the biggest, Fig.4 The filling dependence of the effective quasistatic permeability for Ce2Fe17N3−δ composite. The squares are experimental data;[18]the line and inverted triangle is the calculate data based on Eq.(16);The line and dot is the calculate data based on Eq.(10);The line and triangle is the calculate data base on Bruggeman equation. In Fig.3,we see for both µc> µmand µc< µmthe effective permeability of composite material obtained by energy method is bigger than the one by Maxwell-Garnett method. increases withf.When µc≫ µmandf→0.5,the effect of the magnetic dipole of the particle is the biggest, When µc≫ µmorµc≪ µm,the effect of the magnetic dipole of the particle should not be ignored.For these situation,the energy method is more feasible to calculate the effective permeability of the composite material.It can also be seen in Fig.3 that the difference of the two methods is not significant whenµc≈µmorfis small.For this kind of situation,Maxwell-Garnett method is really simple and feasible. Figure4is the comparison of Maxwell-Garnett method,Bruggeman method,energy method,and experiment result.It can be found that the energy method’s result is in agreement with the experiment.[18] For the composite material filled by superconductor particles,no matter how to change the volume ratio of particles,we will have µeff≤µmfor the Maxwell Garnett method and the energy method,because of the Meissner effect,[44]µc=0.Thus,superconductor particles cannot be used to increase the permeability of the composite material,but they can help to decrease the permeability of the composite material. We have discussed the Maxwell-Garnett and the energy method for calculating the effective permeability of ideal two phase composite material ideally as above.But actually,in the composite material there will have an interface layer between particle and medium of one nanometer thickness.The interface layer is neither particle nor medium.When the size of the particle is big,the effect of interface layer in electromagnetic properties of composite material can be ignored.But the effect of interface layer on electromagnetic properties of composite material cannot be ignored when the size of the particle is small,especially when the size of the particle is nano-sized.When the particles are of nano-size,it is valuable to observe the effect of the physical properties of the interface layer to the effective electromagnetic properties of the composite material.[45] As the model of the composite material in Fig.1(b),letR1be the radius of the particle with the interface layer enclosed,anddbe the thickness of the interface layer.Then the core sphere has a radiusR=R1−d with the interface layer excluded.The volume of the interface of the particles isV2.The permeability of the interface layer isµs.The magnetic intensity of the interface isH2,and the magnetic induction of the interface isB2.The definition of other parameters are the same as Sec.2. We will calculate the magnetic scalar potential in the semi-analytical multi-pole method.Following the multipole technique,[46−47]we set all the poles at the center of the particle for the magnetic scalar potentialφ(r).The static magnetic field in the core,in the interface layer and in the media satisfy the Laplace equation as Eq.(18).The general solution is Eq.(19),1,2,3,...)are the coefficients of the general solution,which must satisfy the boundary-value relation and boundary condition. According to the asymptotic boundary condition and the boundary-value relation atr=Randr=R1,coefficients in Eq.(19)in all domains can be exactly determined for this system.And the unique solution with all nonzero coefficients can be calculated: Then,we get the magnetic intensity of the core,interface and media,respectively. It can be seen from Eq.(22)that the magnetic dipole moment M and magnetization intensitym of the magnetic dipole. The effective permeability can be obtained in the same way from the energy method in Sec.3, If the particle is made of superconductor material,because of the Meissner effect,we takeµc=0in above equations and obtain the effective permeability for the composite material. The effective permeability of composite materialµeff−Win Eq.(25)depends on the permeability of the particlesµc,µs,µm,the volume fractionf,the particle sizeR,and also the thickness of the interface layerd.While in Secs.2 and 3,the interface layer were not considered,and the estimations there missed the particle size dependence. By taking the limitR→0,the complex equation(25)recovers the result given in Eq.(16).The interesting point here is in the limitR→R1,in the behavior for thin layers.InR→R1limit,we can also recover Eq.(16)for bare magnetic balls in the medium.For µeff−Wequation,ifd is small but nonzero,the approximated magnetic scalar potential coefficients in Eq.(21)for the interface layer is: Therefore,for smalld,the uniform component of the local magnetic field in interface layer is µm/(µc+2µm)is the property of the medium and the particle.The interface layer gives proportional factorsµc/µs+2and µc/µs−1,which enhances the local magnetic field.For smallµs,this factor can be big. The thicknessd interacts with particle property through the volume average for the layer fi rst.The effective permeability up to the leading orders of the relative thickness of the interface layer can be easily derived from the following equation, Fig.5 The e ff ect of the interface layer of magnetic balls given by equation(28). µe ff−W(f,d/R1)/µe ff−W(f,0)vs. volume ratiofis plotted for parametersd/R1=0.05,0.1,0.2,µs/µm=0.25,4.We choose µc/µm=2for all curves.Whend/R1is big,µe ff−W(f,d/R1)increases much from µe ff−W(f,0)ifµs>µc,and decreases much ifµs<µc. We display the e ff ect of the interface layer in Fig.5,which plots Eq.(28). In Fig.5,it can be seen thatµeff−W(f,d/R1)increases or decreases along with the increase of filling factor,and this can be controlled by the sign of µs− µc.The change of µeff−W(f,d/R1)is big for small particles.For nano-sized particles,letR1be about 5 nm anddof the order 1 nm,thed/R1=0.2curves in e Fig.5 show much improvement ofµeff−Westimation after we consider carefully the interface layer. We plot Fig.6 for special cases with µc≫ µmorµc≪ µmthrough Eq.(28). It can be seen thatµeff−W(f,d/R1)/µeff−W(f,0)curves all tend to 1 when µc≫µmorµc≪µm.For these cases,the influence of the interface layer to the effective permeability can be ignored. In this study we show the essential features of the mechanism of the interface layer.A fine tuning ofdandµscan be guided by the effective permeability expression in Eq.(25),then one can produce material with a targeted permeability.In this study,the energy method is proposed for calculating the effective static permeability of composites.The effect of interface layer has been fully demonstrated and discussed with the help of magnetic particles and superconductor particles.The predicted effective permeability of composite material based on the energy method agrees with experimental.These results encourage applications of energy average method and interface layer model in design,fabricating,and analysis of particle dispersed composite materials. Fig.6 The influence of the interface layer when µc≫µmor µc≪µm.Allµeff−W(f,d/R1)/µeff−W(f,0)curves tend to 1.Thus,the influence of the interface layer to the effective permeability can be ignored. [1]J.H.Hannay,Eur.I.Phls.4(1983)141. [2]H.A.Lorentz,Annalen Der Physik 245(2010)641. [3]J.C.M.Garnett,Trans.Roy.Soc.53(1904)385. [4]J.C.M.Garnett,Phil.Trans.R.Soc.London 205(1906)237. [5]A.Sihvola,IEEE Electromagn.Waves Series 47(1999)63. [6]Giordano Stefano,J.Electrostat.58(2003)59. [7]D.A.G.Bruggeman,Annalen der Physik 5(1935)636. [8]L.Tsang and J.A.Kong,Theory of Microwave Remote Sensing,John Wiley&Sons,New York 6(1985)pp.575–602. [9]R.E.Meredith and C.W.Tobias,J.Appl.Phys.32(1961)132. [10]T.Liu,P.H.Zhou,L.J.Deng,and W.Tang,J.Appl.Phys.106(2009)3401. [11]V.A.Markel,J.Opt.Soc.America A 33(2016)1244. [12]V.A.Markel,J.Opt.Soc.America A 33(2016)2237. [13]C.Brosseau,J.Appl.Phys.91(2002)3197. [14]V.B.Bregar,Phys.Rev.B 50(2005)174418. [15]V.Boucher,L.P.Carignan,T.Kodera,et al.,Phys.Rev.B 80(2009)308. [16]J.Jin,S.Liu,Z.Lin,and S.T.Chui,Phys.Rev.B:Condensed Matter 80(2009)115101. [17]A.V.Goncharenko,Phys.Rev.E 68(2003)041108. [18]W.L.Zuo,L.Qiao,X.Chi,et al.,J.Alloy.Compd.509(2011)6359. [19]A.Bordianu,L.Petrescu,and V.Ionita,J.Phys.:Conference Series 585(2015)012003. [20]B.Drnovsek,V.B.Bregar,and M.Pavlin,J.Appl.Phys.103(2008)335. [21]Z.Hashin and S.Shtrikman,J.Appl.Phys.33(1962)3125. [22]Z.Qu,S.Liu,Q.Wang,et al.,Comput.Mater.Sci.88(2014)145. [23]L.Wu and S.Pan,Compos.Sci.Technol.72(2012)1443. [24]H.Waki,H.Igarashi,and T.Honma,IEEE Trans.Magn.41(2005)1520. [25]J.J.Wang,Y.Song,X.Q.Ma,et al.,J.Appl.Phys.117(2015)4184. [26]J.Lam,J.Appl.Phys.60(1986)4230. [27]T.M.Simon,F.Reitich,M.R.Jolly,et al.,J.Intel.Mat.Syst.Str.10(1998)872. [28]J.E.Martin,E.Venturini,J.Odinek,and R.A.Anderson,Phys.Rev.E 61(2000)2818. [29]H.M.Yin and L.Z.Sun,Acta Mater.54(2006)2317. [30]H.Zhang and X.Wang,Smart Mater.Struc.23(2014)045009. [31]Y.L.Jiang,Int.J.Engineering Sci.38(2000)1993. [32]K.S.Yee,IEEE Trans.Antennas Propag.14(1966)302. [33]B.Patel and T.I.Zohdi,Mater.Des.94(2016)546. [34]Y.Pittini-Yamada,E.A.Périgo,Y.Hazan,et al.,Acta Mater.59(2011)4291. [35]X.Huang,Y.M.Xie,B.Jia,et al.,Struc.Multidiscip.Opt.46(2012)385. [36]Y.Ito and H.Igarashi,IEEE Trans.Magn.49(2013)1953. [37]J.H.Paterson,R.Devine,and A.D.R.Phelps,J.Magn.Magn.Mater.196–197(1999)394. [38]M.Anhalt and B.Weidenfeller,J.Appl.Phys.105(2009)023907. [39]Ge Fuding and Zhu Jing,Aerosp.Mater.Technol.5(1996)42(in Chinese). [40]Peng Weicai and Chen Kanghua,Rare Metal Mat.Eng.34(2005)1407(in Chinese). [41]J.S.Choi and J.Yoo,Int.J.Numer.Meth.Eng.82(2010)1. [42]A.Thabet,M.A.Abdel-Moamen,and S.Abdelhady,PSC.IEEE(2016)52. [43]M.Barski and A.Muc,Mech.Compos.Mater.47(2011)387. [44]W.Meissner and R.Ochsenfeld,Die Naturwissenschaften.21(1933)787. [45]T.Xiang,Q.Zheng,and S.Qin,IEEE Trans.Dielectr.Electr.Insul.24(2017)1197. [46]Q.Zheng,F.Xie,Y.Yang,and W.Lin,J.Electromagn.Wave.13(1999)1153. [47]J.N.Sheng,Q.S.Ma,B.Yuan,et al.,Theory and Application of Semi-analytical Method in Electromagnetic Fields and Waves,Chinese Academic Press,Beijing(2006)pp.45–49.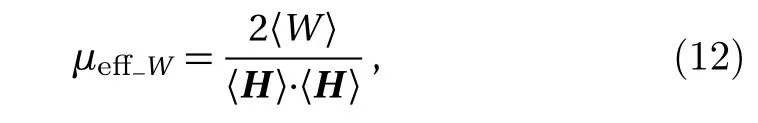
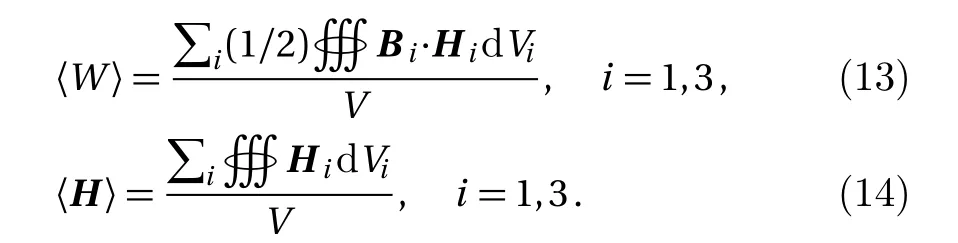
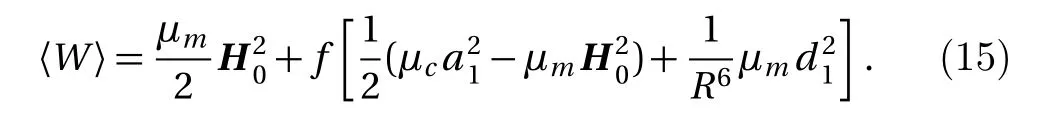
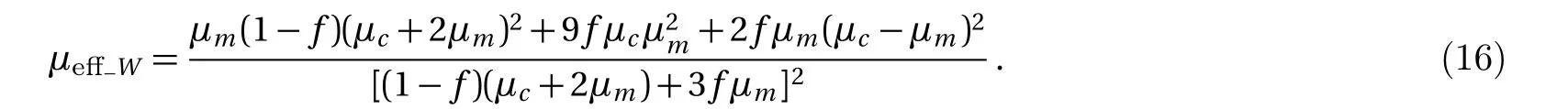
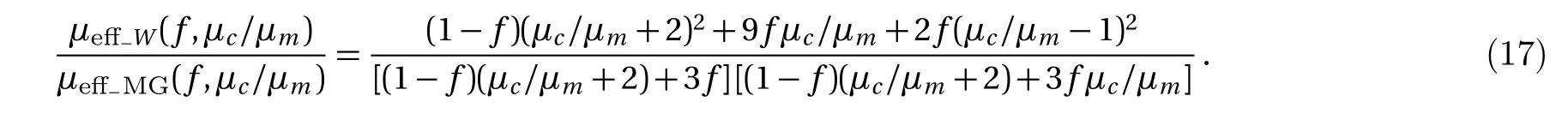
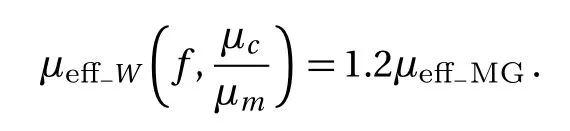
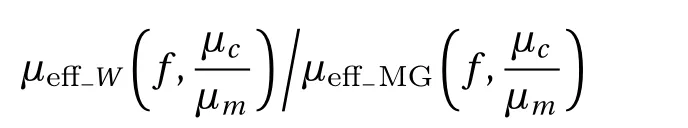
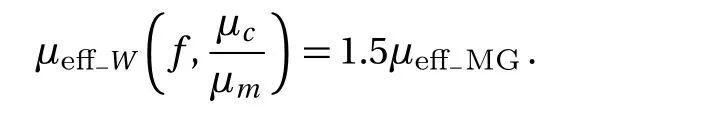
4 Interaface Layer for Particle
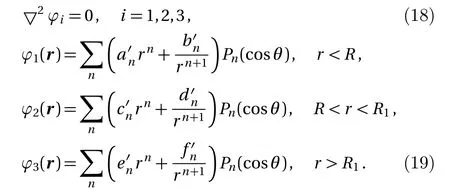
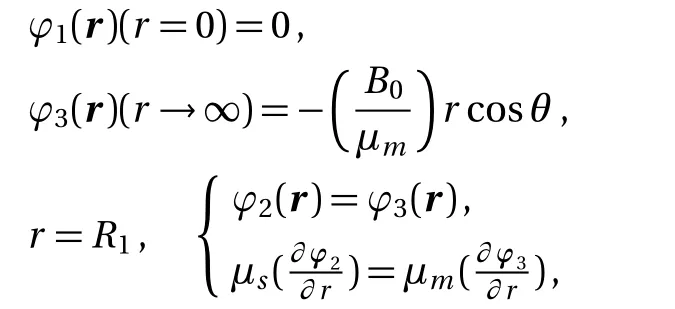
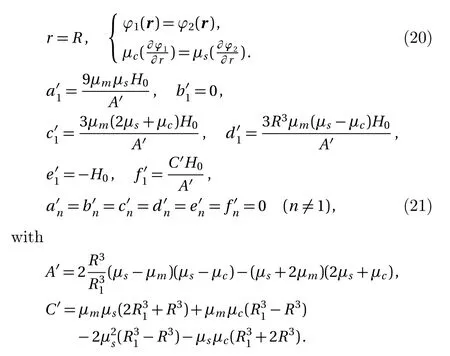
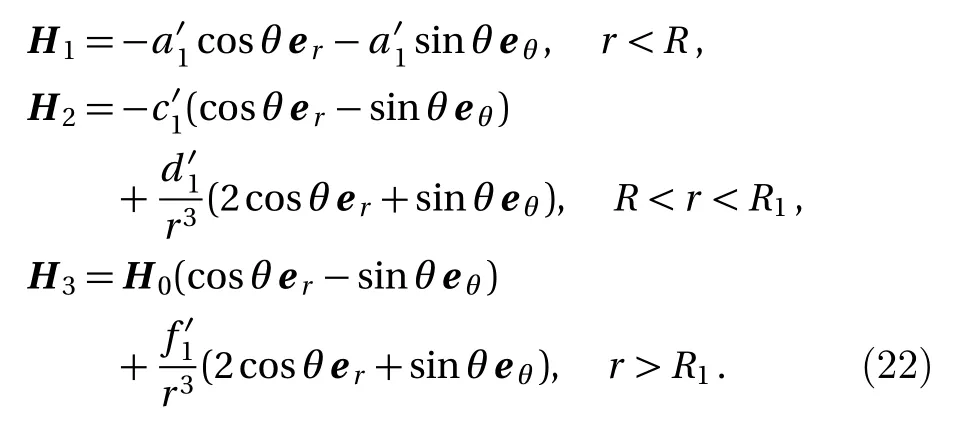
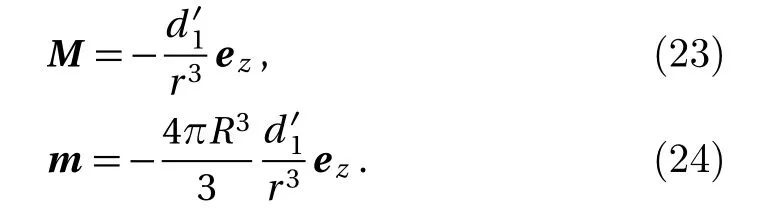
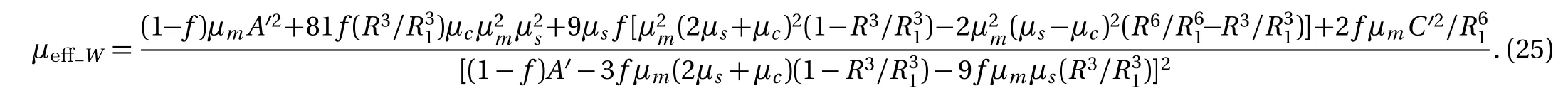
5 Discussion and Conclusion
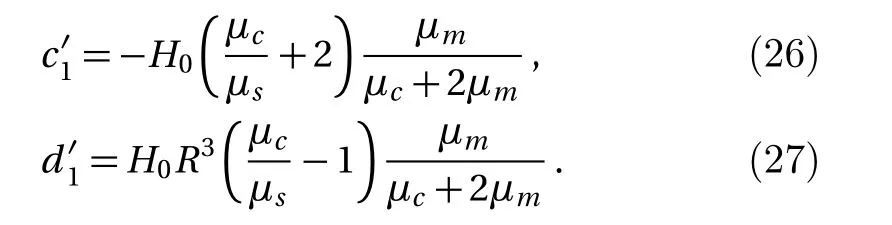
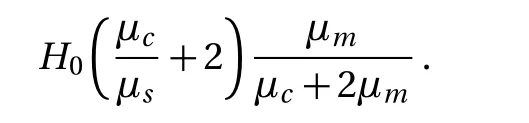
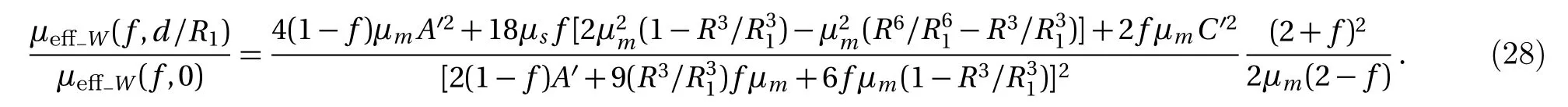
 Communications in Theoretical Physics2018年5期
Communications in Theoretical Physics2018年5期
- Communications in Theoretical Physics的其它文章
- Searches for Dark Matter via Mono-W Production in Inert Doublet Model at the LHC∗
- Electrical Properties of an m×n Hammock Network∗
- On the Generalized Heisenberg Supermagnetic Model∗
- New Double-Periodic Soliton Solutions for the(2+1)-Dimensional Breaking Soliton Equation∗
- Study on the Reduced Traffic Congestion Method Based on Dynamic Guidance Information∗
- Modeling Chemically Reactive Flow of Sutterby Nano fluid by a Rotating Disk in Presence of Heat Generation/Absorption
