高架轨道交通对敏感场地微振动影响控制研究

■ 陈晓坚

0 引言

随着我国城镇化率不断提高，城市人口骤增，带来了巨大的交通出行压力。轨道交通因其自身运量大、快捷、安全、舒适、低能耗等优点被视为解决城市出行问题的最佳方式之一。截至2018年1月1日，我国内地已有35个城市开通城市轨道交通，总里程超过5 000 km。高架线路具有节约土地资源、建设成本低、维修养护方便、适应多种地形地质条件等优点，在城市轨道交通中得到广泛应用。武汉轨道交通1号线是全高架的快速轨道交通线路，上海明珠线高架桥梁约占线路总长86．0%，广州地铁4号线高架桥梁占线路总长69．3%，西安地铁13号线、成都地铁2号线线路也大量采用了高架桥梁。

轨道交通引起的环境振动问题日益凸显，列车激励所引起的结构振动通过周围土体向外传播，进一步诱发建筑物的二次振动，特别是对高层建筑、古旧建筑物、精密仪器生产车间的影响较大。

国内外对高架轨道交通车辆引发的环境振动问题开展了大量研究。Xia等[1-2]对高架轨道交通引起线路附近的地基和建筑物振动进行了现场试验，得到了环境振动与车速、列车轴重与测点距离等参数的关系，并研究了地面各方向的振动衰减规律。张志俊[3]提出了列车-轨道-桥梁垂向耦合振动分析模型、三维桩基-地基耦合振动分析模型以及高速铁路桥梁段车致地面振动问题的频域分析模型。Kouroussis等[4]对布鲁塞尔某铁路所引起的环境振动进行了现场测试并数值仿真分析，研究结果表明，车致地面振动与土体结构、列车类型和速度、测量方向及轨道质量密切相关。李克飞等[5]对北京地铁5号线高架桥减振措施实际效果进行了现场测试。李小珍等[6-7]对成灌线高架桥车致环境振动和高架车站车致振动进行了现场实测。刘维宁等[8]针对地铁列车振动环境影响的预测问题，提出了一种新型深孔激振实测传递函数预测方法。

1 工程概况

某城市轨道交通受到地理环境、车站选位、最小曲线半径等因素制约，紧邻某微电子厂房。该轨道交通线路距某微电子厂房的最近距离约65 m，距某城市道路（双向6车道）约90 m。该路段均采用高架线路，线路自车站引出后由（28+5×30+2×35）m简支梁和（3×41+40）m连续梁跨越至城市道路另外一侧。

考虑微电子厂房未来发展的需要，确保轨道交通运营不影响厂房正常生产，提出轨道交通在运行过程中引起厂房邻近敏感场地振动不超过VC-C标准（平均方式为峰值保持）的控制目标，即允许振动量为1～80 Hz内速度不超过12．5 μm/s。

首先在拟建轨道交通场地开展振动传递特性现场试验，测试重卡经过城市道路时所引起的地面振动，对既有场地振动现状进行评估并研究振动衰减规律。基于列车-轨道-桥梁耦合振动分析理论建立振源分析模型；利用有限元法建立墩-桩-土传播路径模型；预测减振垫浮置板道床、钢弹簧浮置板整体道床2种轨道结构形式下地面环境振动速度，探讨是否满足环境振动要求。该路段紧邻车站，加速、减速、匀速工况众多，研究仅分析靠近厂房一侧单线行车、车速70 km/h的情况，并将其视为最不利的情况。

2 场地土体振动传递特性试验

2.1 试验方案

交通系统引起振动传播和衰减主要在土体中完成，了解工程现场土体振动传递特性是进行振动控制的前提。尽管已取得了较为完善的场地钻探资料，但由于场地土差异性较大，仅凭少数钻孔仍无法全局把握场地土的整体动力学参数。为研究振动在拟建轨道交通场地中的传播规律，开展地面振动传递试验。

场地土体振动传递特性现场测试断面垂直于拟建轨道交通线路。测试断面地表有杂草以及低矮树木，工厂围墙内部为沥青路面或草坪。该测试断面共布置7个测点，编号1#—7#，分别距城市道路边缘0、10、20、30、40、50及65 m，其中1#测点位于海翔大道辅道外侧边缘（见图1）。每个测点布置3个891-Ⅱ型拾振器，分别为X、Y、Z方向。891-Ⅱ型拾振器主要用于测量地面、结构物的脉动或工程振动。对于振动速度，通频带为1～80 Hz，分辨率为2×10-8m/s。

试验利用道路重型卡车激励，车速60～80 km/h，采集多组重型卡车经过时各测点振动速度样本，选取20组典型有效数据进行统计分析。为减小周围其他振源的影响，试验选在夜间进行。

2.2 测试结果

X、Y、Z 3个方向本底振动测试结果见图2。可以看出，本底振动主要集中在0～40 Hz，均小于VC-C标准。

重型卡车经过时，3个典型工况振动测试结果见图3。

图1 测点布置

图2 本底振动数据

图3 汽车激励所引起场地振动

由图3可知：

（1）当重型卡车经过测试断面时，1#—7#测点处垂向振动速度均远超过VC-C标准，7#测点处垂向振动速度20～30 μm/s；

（2）对于水平振动，当重型卡车驶过4#测试断面时，7#测点（65 m）处振动速度低于10 μm/s，满足VC-C标准；

（3）2#、3#、4#测点10～40 m处振动速度反而大于1#测点，说明水平振动速度在一定距离范围内有放大趋势。

基于1#—7#测点振动测试结果，可掌握该敏感场地目前振动污染状况，并可验证数值仿真分析模型中土体振动传递衰减规律。

3 理论分析

高架轨道交通引起环境振动的理论分析思路见图4，理论分析模型包括振源模型和传播路径模型。对于振源模型，基于列车-轨道-桥梁耦合振动分析理论[9-10]，求解出时域轮轨力进行傅里叶变换得到频域轮轨力。将频域轮轨力施加在轨道-桥梁有限元模型中进行谐响应分析，得到频域支座反力；对于传播路径模型，建立墩-桩-土模型，在墩顶施加振源模型中所求出的支座反力。

数值仿真模型建立3跨30 m简支梁，箱梁跨中截面见图5。该混凝土梁为双线混凝土单箱单室箱梁，梁宽10．20 m，线间距4．20 m，跨中截面梁高2．00 m、顶板厚0．25 m、腹板厚0．35 m、底板厚0．27 m。主梁采用C50混凝土。桥墩为多边形截面实心墩，标准截面为2．4 m×2．2 m，采用C40混凝土，墩高10 m。采用4根直径1．2 m钻孔灌注桩基础，桩长35 m。

3.1 预测模型

3.1.1 振源模型

图4 理论分析思路

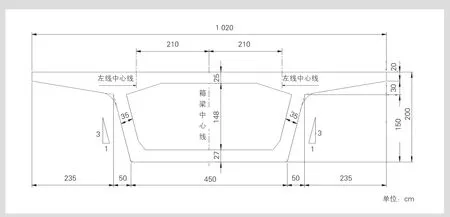
图5 箱梁跨中截面

为准确求解时域轮轨力，建立列车-轨道-桥梁振动模型。车辆采用地铁B型车，6节编组，每节车厢有4个轮对、1个车体，简化为刚体；一系、二系悬挂简化为弹簧阻尼元件；轨道不平顺采用美国五级谱，车速70 km/h。将时域轮轨力进行傅里叶变换，得到各轮对频域轮轨力，频率1～90 Hz。

为求解最大支座反力，建立轨道结构-桥梁动力分析模型（见图6）。钢轨采用60 kg/m标准轨，简化为梁单元；轨道板、底座板、桥梁等均简化为板单元；扣件、钢弹簧简化为弹簧阻尼单元。划分网格大小约为0．5 m，扣件间距取0．6 m，扣件刚度取60 kN/mm。支座通过施加自由度约束实现，简支梁一端两支座简化为1个约束单元。桥梁轮轨力加载最不利位置见图7，将2#墩支座反力视为最大值，相邻两节车紧邻的两轮对对称施加在2#墩两侧桥梁上。通过谐响应分析，求解得到2#墩墩顶两支座反力，分析频率1～90 Hz。

3.1.2 墩-桩-土传播路径模型

建立墩-桩-土传播路径模型（见图8），土体大小为平行于线路方向100 m，垂直于线路方向100 m，深40 m，桩长35 m。承台顶部与土体表面平齐，桩土共节点处理。有限元模型采用实体单元建模，划分网格大小0．5～1．0 m。为保守起见，将所求2#墩墩顶两支座反力施加在墩-桩-土模型1#—4#墩墩顶。通过谐响应分析，求解2#、3#桥墩中间距线路65 m处地面振动响应。

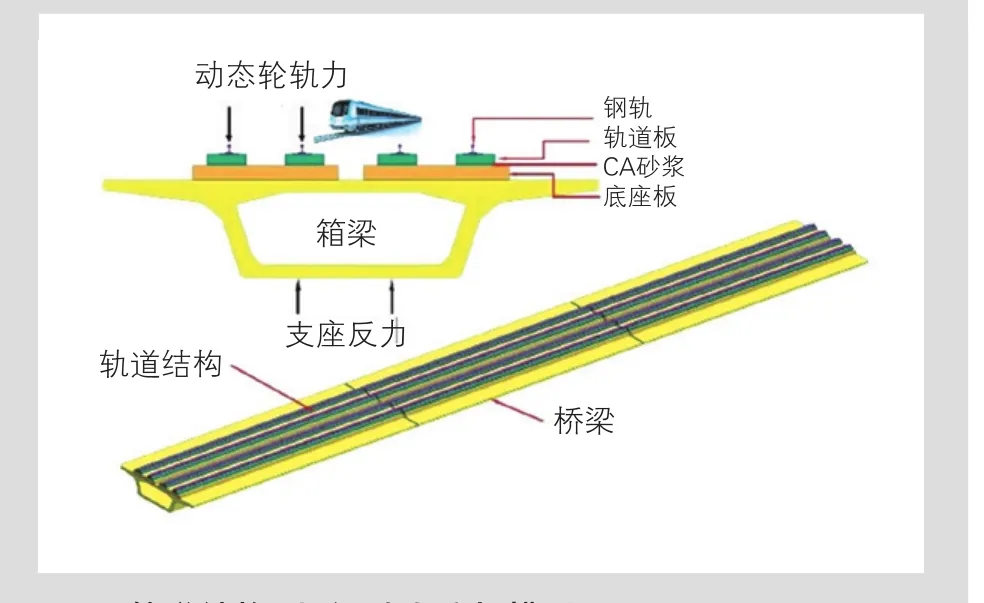
图6 轨道结构-桥梁动力分析模型

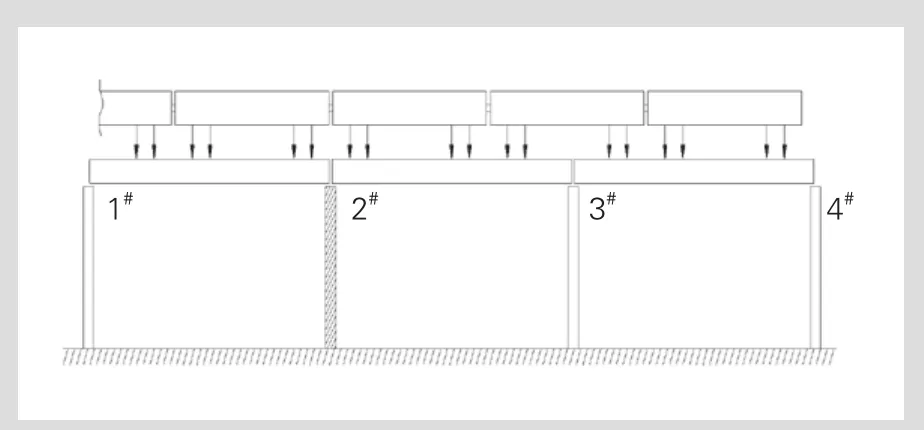
图7 桥梁轮轨力加载最不利位置

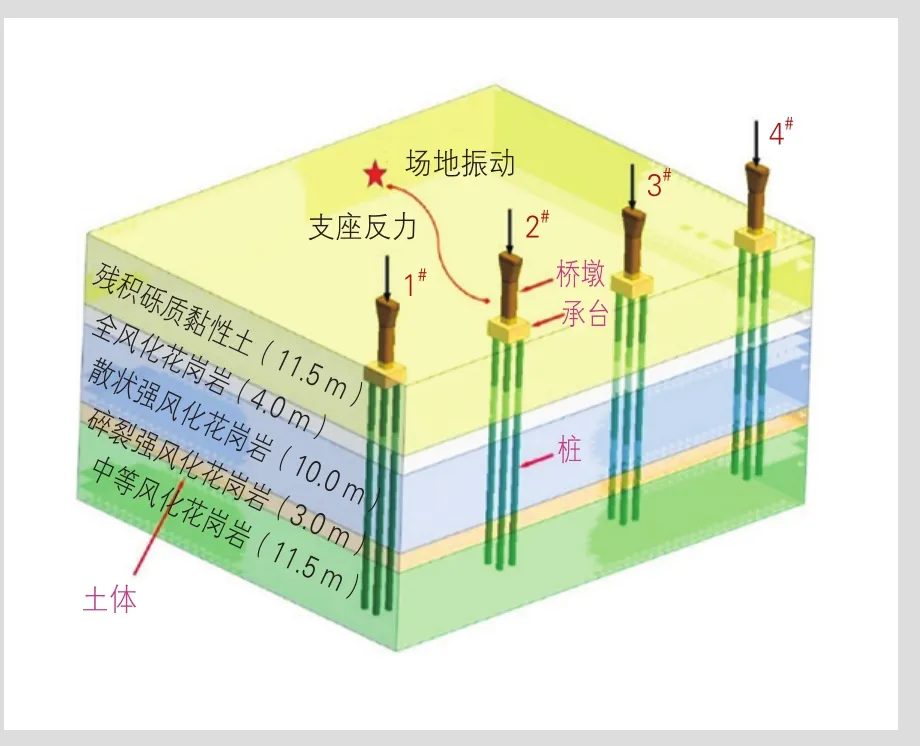
图8 墩-桩-土传播路径模型

3.2 场地土体振动衰减规律验证

验证思路：在已建传播路径模型中施加一虚拟简谐力模拟汽车荷载，调整简谐力大小，使力作用点附近振动与1#测点处实测汽车激励作用下振动相似，然后对比传播路径模型中振动传递至65 m振动速度衰减量与实测汽车激励下振动速度衰减量平均值是否一致。

选取汽车激励引起场地振动多个工况测试结果平均值作为已知振动（1#测点），并得到振动经场地土体传递至65 m时振动衰减量。由于实测汽车激励下场地土体水平方向振动较小，仅对垂直Z方向振动衰减规律进行验证。

振动计算值与实测值对比见图9，计算衰减量与实测衰减量对比见图10。可以看出，在振源附近垂直方向振动速度相似的前提下，振动衰减至65 m处振动衰减量实测值与计算值基本吻合，传播路径模型能够较准确地模拟场地土体振动衰减规律。

4 不同道床的地面振动响应

轨道既是引起列车振动的主要振源之一，也是承担和传递振动的第一子结构。因此轨道的结构形式、材料组成及其相应的动力特性极大地影响着轨道交通环境振动的特性。轨道结构形式的动力特性随着轨道单元的质量、刚度和阻尼的不同而改变。改变轨道的动力特性意味着直接改变了振源的频率组成及振动强度。对轨道结构动力特性的合理优化，可设计出不同的减振轨道产品；相反，不合理的设计会恶化轮轨相互作用关系。

4.1 减振垫浮置板道床

减振垫浮置板道床即在轨道板与底座板之间加入橡胶减振垫，每块道床板对应1块基底，每块基底两端在线路中线处各设置1个限位凸台。每块轨道板长5．875 m，相邻两轨道板间距0．15 m。单位面积橡胶减振垫刚度为6．0 kN/mm，厚度为30 mm。在轨道-桥梁有限元模型中，每延米橡胶减振垫简化为2个弹簧，连接钢筋混凝土基底和轨道板，垂向刚度为7．2 kN/mm。

图9 振动计算值与实测值对比

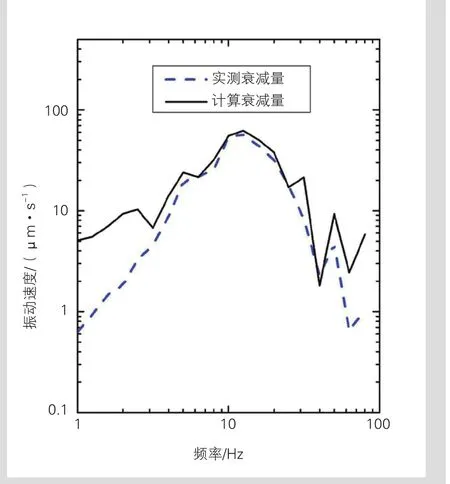
图10 计算衰减量与实测衰减量对比

减振垫浮置板道床结构在单线行车、车速70 km/h的工况下，距线路65 m处地面振动速度见图11。

由图11可知：

（1）列车轮轨荷载激励下，地面垂向振动速度比水平方向振动速度大；

（2）地面振动频率主要集中在5～30 Hz，峰值在10 Hz附近；

（3）距线路65 m处，两水平方向振动速度均低于VC-C标准，而垂向振动速度20～30 μm/s，高于VC-C标准。

4.2 钢弹簧浮置板整体道床

钢弹簧浮置板道床即在轨道板和桥梁间插入一钢弹簧隔振器。轨道板长29．960 m，厚约0．475 m，宽2．800 m。钢弹簧隔振器间距1．8 m，垂向刚度5．43 k N/m m，横向刚度4．10 k N/m m，阻尼比为5%～10%。

钢弹簧浮置板整体道床结构在单线行车、车速70 km/h的工况下，距线路65 m处地面振动速度见图12。

由图12可知：

（1）相对于减振垫浮置板道床，钢弹簧浮置板整体道床能够有效降低车致地面振动；

（2）对于钢弹簧浮置板整体道床轨道结构，距线路65 m处，3个方向振动速度均低于VC-C标准。

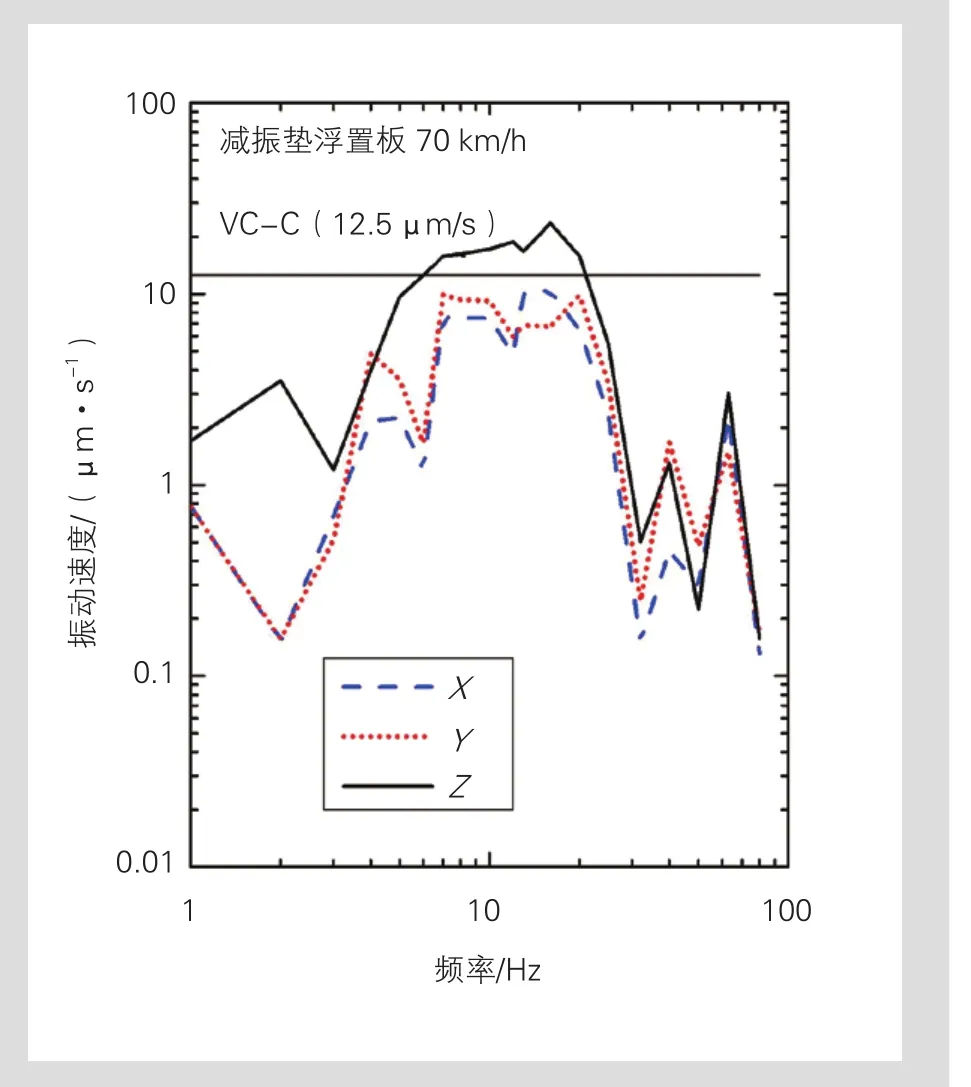
图11 减振垫浮置板道床地面振动响应

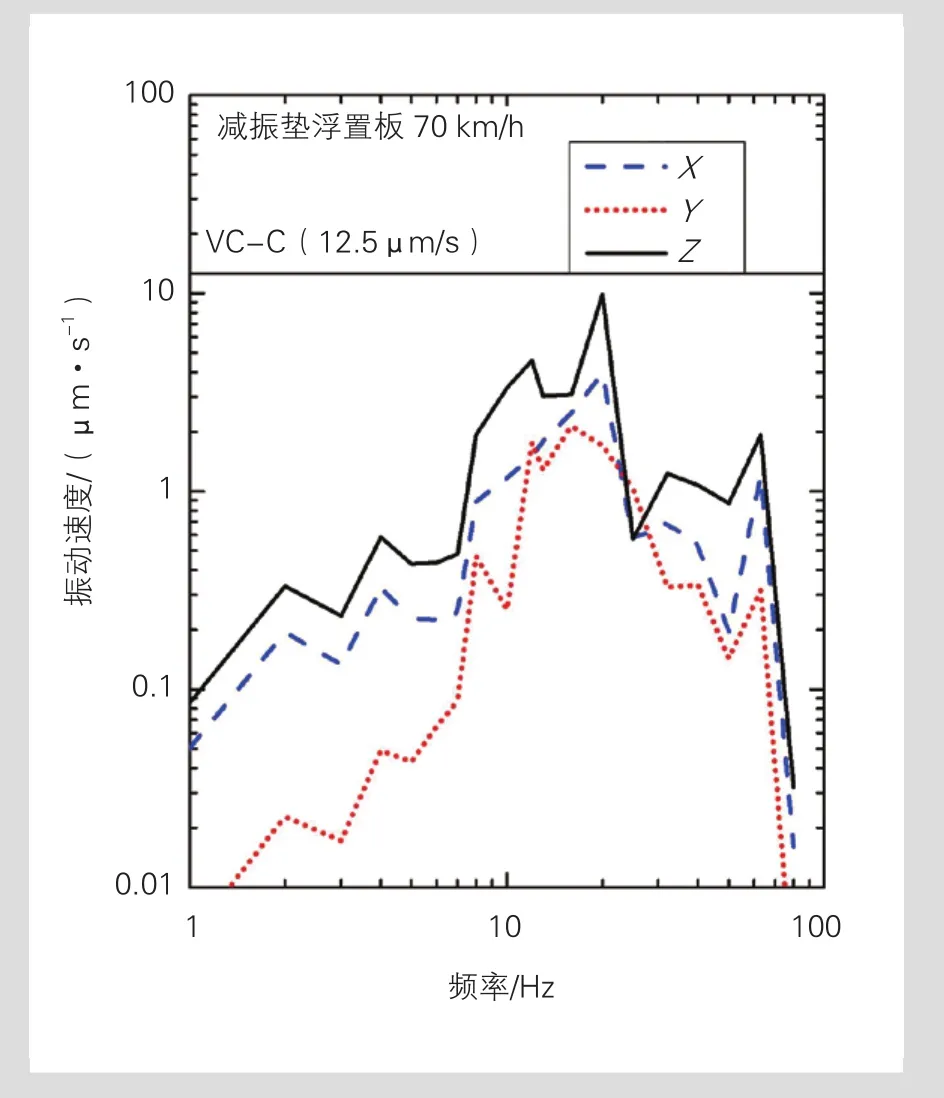
图12 钢弹簧浮置板整体道床地面振动响应

5 结论

高架轨道交通所引起的地面振动与场地条件、车辆、桥梁轨道结构等因素息息相关，研究思路、成果可为类似工程提供参考。主要结论有：

（1）当重型卡车经过时，距城市道路边缘65 m处垂向地面振动速度20～30 μm/s，水平振动速度低于10 μm/s；

（2）通过振源模型以及墩-桩-土传播路径模型，可预测高架轨道交通引起的地面环境振动；

（3）在单线行车、车速70 km/h的情况下，当采用减振垫浮置板道床结构时，距线路65 m处垂向地面振动速度20～30 μm/s，且频率主要集中在5～30 Hz；

（4）在单线行车、车速70 km/h的情况下，当采用钢弹簧浮置板整体道床结构时，距线路65 m处X、Y、Z方向地面振动速度均低于VC-C标准（12．5 μm/s）。

[1] XIA H，ZHANG N，CAO Y M． Experimental study of train-induced vibrations of environments and buildings[J]． Journal of Sound & Vibration，2005，280(3)：1 017-1 029．

[2] XIA H，CHEN J G，XIA C Y，et al． An experimental study of train-induced structural and environmental vibrations of a rail transit elevated bridge with ladder tracks[J]． Proceedings of the Institution of Mechanical Engineers：Part F：Journal of Rail & Rapid Transit，2010，224(3)：115-124．

[3] 张志俊．高速铁路桥梁段车致地面振动的半解析分析与试验研究[D]．成都：西南交通大学，2016．

[4] KOUROUSSIS G，CONTI C，VERLINDEN O．Experimental study of ground vibrations induced by Brussels IC/IR trains in their neighbourhood[J]．Mechanics & Industry，2013，14(2)：99-105．

[5] 李克飞，刘维宁，孙晓静，等．北京地铁5号线高架线减振措施现场测试与分析[J]．中国铁道科学，2009，30(4)：25-29．

[6] 李小珍，刘全民，张迅，等．高架轨道交通附近自由地表振动试验研究[J]．振动与冲击，2014，33(16)：56-61．

[7] 李小珍，刘全民，张迅，等．铁路高架车站车致振动实测与理论分析[J]．西南交通大学学报，2014，49(4)：612-618．

[8] 刘维宁，陈嘉梁，吴宗臻，等．地铁列车振动环境影响的深孔激振实测传递函数预测方法[J]．土木工程学报，2017(9)：82-89．

[9] 翟婉明，夏禾．列车-轨道-桥梁动力相互作用理论与工程应用[M]．北京：科学出版社，2011．

[10] 李小珍，刘德军．车辆-桥梁耦合动力学理论与工程应用[M]．北京：科学出版社，2017．