新中考对策：“立足基础 关注过程 能力为重 全面培养”——2017年福建省中考启示

（南平市松溪县第二中学 福建松溪 353500）

中考不只考学生，从教师角度来看，也考老师，考老师的备考，更考老师的平常教学。因此我们首先要对命题的思想、依据、性质、价值有个大致了解。[1]

研究2017年福建省中考数学试题，初步把握以上特点，结合自己近十几年的教学经验，个人认为至少从以下几方面进行教学是非常必要的。[2]

一、立足基础

全卷以基础知识为立足点，充分考查学生对“四基”即基础知识、基本技能、基本思想、基本数学活动经验扎实情况。三大题型都体现这一特点：

例1 （1）3的相反数是（ ）.

（A）-3 （B）（C）（D）3

（2）用科学记数法表示136 000，其结果是（ ）.

（A） 0.136×106（B）1.36×105

（C） 136×103（D） 1.36×106

[评析]（1）题考查的是相反数概念，答案是A.（2）题考查的是科学记数法，答案是B.这三道题考查的都是基础知识，几乎每一题中都只有一个知识点.学生只要明白这个知识点，便可解答.

1. 对策：教学时，讲透四大领域中“数与代数”“图形与几何”“统计与概率”“综合与实践”中的所有知识点，要让学生过关记忆，理解记忆，运用记忆。[3]

例2：（1）关于图形对称性的命题正确的是（ ）.

（A）圆既是轴对称图形，又是中心对称图形

（B）正三角形既是轴对称图形，又是中心对称性图形

（C）线段是轴对称图形，但不是中心对称图形

（D）菱形是中心对称图形，但不是轴对称图形

（2）不等式组的解集是（ ）

（A）32x-≤≺ （B）32x-≤≺ （C）2x≥ （D）3x-≺

[评析] （1）题考查的是对称性，答案是A.

（2）题是不等式组的解集，答案是A.

这两道题是将三个或三个以上的知识点融合在一道题里，难易程度与上面题相比又有差别，随着融合的知识点增多而难度加大。

2．对策：教学时，除上面的对策之外，还应加强对知识点之间联系，形成相似知识间的小系统，由点到面，再面到点辨证联系，逐步形成大系统。

二、关注过程

关注过程，关注学生在数学学习过程中对数与式的运算、整式的变形、列方程、解方程、列不等、解不等式、画函数图象、尺规作图等.通过学生亲身经历数学活动过程所获得的具有个性特征的经验：

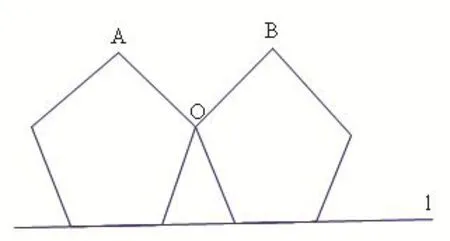
例4 ：（1）两个完全相同的正五边形都有一边在直线l上，且有一个公共顶点O，其摆放方式如图所示，则∠AOB等于_______度.

（2）先化简，再求值：

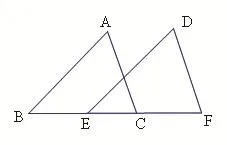
（3）如图，△ABC中，∠BAC=90o，AD⊥BC，垂足为D，

求作∠ABC的平分线，分别交AD，AC于P，Q两点，

并证明AP=AQ.（要求尺规作图，保留作图痕迹，不写作法）

[评析]：（1）利用正五边形的定义，及内角和与邻补角关系，观察、分析得出结果为108O

（2）利分式基本运算技能，展示运算过程，不难得出结果

（3）经历用尺规画角平分线的过程，加演译推理与逻辑推理，利用等腰三角形的判定得到结果

对策一：扎扎实实经历数与式的运算、变形过程是整个数学的基础，明确各学段数与式学习重点，让学生进行有计划有步骤训练.同时几何各学段学习重点也应了然于心，经历识图，作图，用图的过程，渐进式地培养学生的逻辑推理，演译推理，为学生的后续学习打好基础。[4]

“黑城”始建于西夏时期，是现今已知唯一一座用党项族语音命名的城市。蒙古语为哈日浩特，是西夏黑水城和元代亦集乃路城遗址。当年在马可·波罗游记中的亦集乃路是一座繁荣的城市。

例5 ：若直线y=kx+k+1经过点（m，n+3）和（m+1，2n-1），且0＜k＜2，则n的值可以是（ ）

（A） 3 （B） 4 （C） 5 （D） 6

[评析]：由已知可得

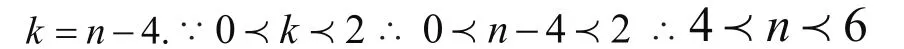
故选C. 解含参数的二元一次方程组，抓住数学本质进行加减消元不受参数影响，通过函数与方程、变量间的关系，求得n的解.

对策二：抓住数学本质，化难为易，这是在一天天的学习中积累的活动经验的应用.，更多的活动经验是间接的，是在学生一天天的学习中积累后得到的顿悟。[5]

两式相减得

三、能力为重

这是的“能力”是广意的，有计算能力、推理能力、观察能力、空间想象能力、抽象能力、问题解决能力、学习能力，它是数学学习的核心，它通过发现问题、分析问题、解决问题得以表现.

例6：（1）（2017年福建省中考第24题）如图矩形ABCD中，AB=6，AD=8，P，E分别是线段AC、BC上的点，且四边形PEFD为矩形.

（Ⅱ）若求CP的长.

（2）（2017年福建省中考25题）已知直线y=2x+m与抛物线y=x2+ax+b有一个公共点M（1，0），且a＜b.

（Ⅰ）求抛物线的顶点Q的坐标（用含a的代数式表示）；

（Ⅱ）说明直线与抛物线有两个交点；

（Ⅲ）直线与抛物线的另一个交点记为N.

（ⅰ）若求线段MN长度的值取范围；

（ⅱ）求△QMN面积的最小值.

[评析]：

（1）以矩形为背景，考查分类讨论思想；通过已知值求目标值，考查相似三角形性质与判定，逻辑推理能力，数学计算能力.这都是学生素养的综合体现，也是未来学习能力强弱的判断依据.

（2）本题题目很短，但内含极丰富.（Ⅰ）考查顶点式，考查学生恒等变形能力，还是要抓住数学本质处理参数能力.（Ⅱ）考查函数与方程的关系，及直线与交点个数反映到△的关系上.

对策三：重视初中所有知识点的学习与理解，重视学习过程，让学生在初中三年的学习过程中的每一堂课的渗透才能积累，发展各种能力.也才会融会贯通，灵活应用，以不变应万变.

四、全面培养

从以上分析可以看出，中考试卷考查可谓面面俱到，素材、载体灵活变化，为不变应万变，我们应全面培养，又由于中考是一场选拔性考试，三年的学习效果，通过两个小时来体现，俗话说养兵千日用兵一时.因此平常要渐渐培养好的学习惯：如心静，专注习惯；自觉订正、反思习惯；写字工整漂亮的习惯；坚持阅读习惯；坚持锻炼身体习惯；甚至于自信乐观习惯等等，教师应在以上方面给予引导、全面培养.

[1] 2011版《初中数学课程标准》.

[2] 张奠宙,于波.〈数学教育的“中国道路”〉.

[3] 邱宗如.说2017年福建省统一中考数学试卷评析.2017福建中学数学第8期.

[4] 贾凤梅,薛红霞.2016年中考总体评价.中国数学教育2017 1-2.

[5]徐帆,黄莉,张胜元.2017年福建省中考数学卷与课程标准的一致性研究.2017福建中学数学第7期.