结合DOEC极小化策略的SAT求解极小碰集方法

王荣全 欧阳丹彤 王艺源 刘思光 张立明

(吉林大学计算机科学与技术学院 长春 130012) (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012) (wangrongquanjlu@163.com)

人工智能专家Console等人[1]指出基于模型诊断(model based diagnosis, MBD)的研究对整个人工智能领域的研究有着重要的作用.学者Struss[2]称基于模型诊断是人工智能领域极富有挑战性和具有检验性的课题.基于模型诊断的核心步骤是根据系统的描述和观测，得到极小冲突集合簇[3]，然后以其为输入并利用碰集(hitting set, HS)的求解方法计算得到系统所对应的极小诊断解即极小碰集(minimal hitting set, MHS)，因此求解MHS问题是模型诊断中比较核心的问题之一[4].此外很多的实际和理论问题都可以转化为MHS问题[5-6]，如极小集合覆盖和极小顶点覆盖等极小覆盖问题均是极小碰集的特殊形式、师生选课问题、蕴涵推理问题以及智能规划的核心问题.

碰集(hitting set, HS)问题最早是由加州大学伯克利分校的计算机专家Karp在1972年提出，随后MBD专家Reiter[7]首次提出了一种求解极小碰集的方法HS-Tree，但该方法基于枚举树并遍历整棵枚举树导致效率较低，且会因剪枝丢失解.因此，Greiner等人[8]提出HS-DAG方法，优化并改进了HS-Tree方法的剪枝策略，虽然解决因剪枝而丢失解，但因新的剪枝规则的应用导致计算复杂度大幅度增加.随着对极小碰集问题的深入探索研究，许多新的求解方法陆续被提出.2001年，Wotawa[9]通过改进HS-Tree方法提出了HST-Tree方法，虽然效率提升，但其通用性降低，并未彻底解决丢解的问题，空间复杂度较高；2003年，姜云飞等人[10]提出布尔代数方法，从解的完备性和方法的高效性来看，该方法是目前较好的求解方法之一，因为其不需要建立较复杂的树结构，只需递归计算字符串操作，比之前所有的方法在空间复杂度和时间复杂度都有降低，在提高求解效率的同时简化了数据结构；2004年，欧阳丹彤等人[11]改进了HS-DAG方法，通过剪枝无解空间达到提高效率，但因数据结构复杂使方法实现繁琐；2006年，赵相福等人[12]提出了HSSE-Tree方法，其利用与元素相关联的冲突集个数来计算碰集并在标准的SE-tree上对节点种类进行标识，从而提高搜索效率；2010年，陈晓梅等人[13]提出了BNB-HSSE方法，采用分支定界法与集合枚举法相结合的方法来降低求解规模；2011年，张立明等人[14]提出了基于动态极大度的DMDSE-Tree方法，其通过结点度概念较早地生成极小碰集，减少了生成结点的数量；2012年，Pill等人[15]对布尔代数方法改进了部分规则，有效提升了该方法对特定问题的求解效率；2015年，王艺源等人[16]提出了利用CSP求解器求解极小碰集的CSP-MHS方法，其思想是通过将求解极小碰集问题转为约束满足问题，然后调用CSP求解器进行求解，并根据约束可满足问题的特点去求解具有某些特征的极小碰集.

以上是求解MHS的完备方法，随着近似求解策略的不断产生和完善，众多的非完备极小碰集求解方法也陆续被提出[17-18].其中大多采用的是随机搜索策略，其特点是牺牲了解的完备性从而能针对规模较大的问题可以在较短时间进行求解.此外，随着并行和分布式的发展，很多学者也开始投入到用并行或分布式的方法去求解极小碰集问题[19-20].

本文在对SAT问题的深入理解与分析的基础上并与极小冲突集合簇求解极小碰集过程的本质相结合，提出利用目前较为成熟的SAT求解器进行碰集求解，把极小冲突集合簇转换表示成SAT求解器的可求解的CNF形式.在每次求解出一个碰集之后利用首次提出的DOEC极小化策略进行极小化，在每次极小化的过程中，先把碰集通过元素覆盖集合度的势找出其中所有的冗余元素，并对其进行删除，从而高效地实现碰集极小化.最后把已经极小化产生的极小碰集以取反的隔离子句的形式添加到CNF中并继续调用SAT求解器进行求解，直到SAT求解器返回不满足，即问题求解.由于每个求出的碰集都被极小化过，并以取反的隔离子句的形式添加到求解器的CNF中，所以在下次求解的过程中不会求解极小化后的极小碰集的求解空间，从而实现了对部分求解空间的屏蔽.但该方法不会屏蔽极小解，从而保证求出所有的解，保证了解的完备性.这种方法的主要优点是：1)因采用宽度优先求解方式，与上述提到的方法相比能较快地得到解；2)减少了对大量非极小化碰集的无用求解，大幅提高方法效率；3)根据SAT求解器的是否满足即可判断求解是否结束；4)仅使用树结构来描述分析问题，实现过程中仅使用数据结构简单的数组描述，所以实现容易.

1 预备知识

在本节，首先介绍下基于模型诊断的基本概念及其相关的基础知识.

1.1 基于模型诊断的相关概念

定义1[7]. 一个系统可定义为一个三元组(SD,COMPS,OBS)，其中：

1)SD为系统描述，是一阶谓词公式集合，SD描述了待诊断系统的相关背景知识;

2)COMPS是系统组成部件的集合，是一个有限常量集；

3)OBS为观测集，是一阶谓词公式的有限集.

定义2[7]. 冲突集CS是一个部件集{c1,c2,…,cn}⊆COMPS当且仅当SD∪OBS∪{AB(c1),AB(c2),…,AB(cn)}是不一致的.其中AB为一元谓词，表示“abnormal”.AB(c)为真，当且仅当c异常，且c∈COMPS.

称冲突集是极小冲突集(MCS)，当且仅当该冲突集的任意真子集都不是冲突集.

定理1[7].Δ是(SD,COMPS,OBS)的一个极小诊断，当且仅当Δ是(SD,COMPS，OBS)的极小冲突集的极小碰集.

1.2 SAT问题的相关定义

可满足问题的一些基本定义如下：

定义3[21]. 文字.对于变量集合X={x1,x2,…,xn}，文字lj是变量xi或者它的否定-xi.

定义4[21]. 子句.子句Cj是文字lj的析取，Ci=l1∨l2∨…∨lm.

定义5[21]. 合取范式(conjunctive normal form, CNF). CNFC是子句的合取，C=C1∧C2∧…∧Ck.

定义6[21]. SAT问题的定义如下：对于n个布尔变量X={x1,x2,…,xn}，找到一组变量的赋值，满足在各个子句中都存在一个文字取真，并且这组赋值使得所有的子句都能取真.若找到这样的赋值，则称该SAT问题是可满足的(SAT)；如果没有任何一组变量赋值使得SAT可满足，则称该SAT问题是不可满足的(UNSAT).

2 集合极小化方法

集合极小化方法在模型诊断中有着举足轻重的作用并且是必备的求解步骤.在模型诊断中的诊断解的求解过程中，其占据大部分求解时间.目前对该问题的求解策略还主要停留在求解效率和时间较为复杂的SSDM极小化策略，因此提出新的极小化策略会在很大程度上提高诊断求解时间和效率.本节提出DOEC极小化策略来进行极小化处理，该策略的优点是其求解复杂性和效率不会随着要求解的问题的碰集个数增加而导致极小性判定时间急剧增加，而是只与待求解的初始极小冲突集合簇的大小相关.

2.1 相关定义

首先给出一些与极小化策略相关的定义.

定义7[10]. 设F是一个集合簇,F={S1,S2,…,Si,…,Sn},称H为F的一个碰集(HS)，如果H满足2个条件：

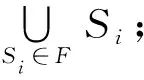
2) 对于任意一个Si∈F，都有HS∩S≠∅.

称F的一个碰集H为极小碰集(MHS)，当且仅当H的任意真子集都不是F的碰集.

定义8. 若num∈Si，则称元素num覆盖集合Si.元素num覆盖集合Si记为Cover(num,Si)={num|num∈Si,num∈H}.含有元素num的碰集H和冲突集合Si取交集后共有的元素个数称为元素num覆盖集合Si的度，简称元素覆盖集合度，记为DOEC(Cover(num,Si))={num|num∈(Si∩H)}.

定义9. 对于碰集H中的元素num，如果其覆盖的所有的Si，均有DOEC(Cover(num,Si))≥2，则称此num是该H的冗余元素.

根据以上定义，我们易得以下推论：

推论1. 如果碰集中不存在冗余元素，则该碰集是极小碰集.

证明. 假设极小碰集中存在冗余元素，则根据冗余元素定义，可知元素覆盖的所有Si，均有DOEC(Cover(num,Si))≥2，即此元素所覆盖的集合也被极小碰集中其他元素覆盖，即当前极小碰集删除此元素后仍为碰集，与极小碰集定义矛盾.

证毕.

针对上面的定义和推论，我们通过实例对提到的元素集合覆盖度、冗余元素、碰集和极小碰集的概念进行进一步说明和阐述.

例1. 冲突集合簇CS={{2,4,5},{1,2,3},{1,3,5},{2,4,6},{2,4},{2,3,5},{1,6}}，要求求其所有极小碰集.首先要极小化，将CS中为某些冲突集合的超集的集合删除，即删除{2,4,5}和{2,4,6},因为它们是集合{2,4}的超集，这样得到一个新的极小化的冲突集合簇CS={{1,6},{2,4},{1,2,3},{1,3,5},{2,3,5}}.通过去除超集，这样可以减少方法处理的节点数目和冲突集的数量，从而进一步提高求解效率.该集合簇的所有的碰集为HS={{1,2},{1,3,4},{1,4,5},{2,3,6},{2,5,6},{2,3,4,5,6},{2,4,5,6},{3,4,6},{3,4,5,6}}.其中{2,3,4,5,6},{2,4,5,6},{3,4,5,6}为非极小碰集，其余的为极小碰集.

例如以是碰集但是是非极小碰集的{2,4,5,6}来说明解析，首先对该非极小碰集进行元素集合覆盖度初始化并计算，计算的覆盖度如下：{1,6}：1，{2,4}：2，{1,2,3}：1，{1,3,5}：1，{2,3,5}：2，然后对{2,4,5,6}的每个元素进行覆盖度访问.

对元素2来说，它覆盖的集合有{2,4},{1,2,3},{2,3,5}其中{1,2,3}的覆盖度为1小于2，所以元素2不是冗余元素，不能将其删除；接着是4，它覆盖的集合只有{2,4}且覆盖度为2，所以根据冗余元素定义，其是冗余元素，可以将其删除；接着是5，它覆盖的集合有{1,3,5}：1，{2,3,5}：2，其中{1,3,5}的覆盖度为1小于2，所以元素2不是冗余元素，不能将其删除；最后是元素6，它覆盖的集合有{1,6}且覆盖度为1，所以不能将其删除.所以将{2,4,5,6}中唯一的冗余元素4删除之后，该碰集为极小碰集.

2.2节对结合元素覆盖集合度的DOEC碰集极小化策略进行详细介绍，然后在第4节对这2种极小化策略实验结果进行比较.

2.2 结合DOEC的碰集极小化策略

本节将给出DOEC的极小化策略，该方法的主要思想是：检查待检测碰集中的每个元素的集合覆盖情况，如果它覆盖的所有原始冲突集合已经都被该碰集中的其他元素覆盖过了，即它所覆盖集合的覆盖度均大于1，则该元素是冗余元素，可以将其删除.不断的继续检查碰集中的每个元素覆盖集合的覆盖度情况，直到被检测的碰集的所有元素都被检测完毕，剩下元素构成新的碰集一定是极小碰集.

算法1. DOEC.

输入:HS={e1,e2,…,ei,…,en};

MHSs={MHS1,MHS2,…,MHSm};

输出:极小化后的碰集HS.

①Covers∅;

② for eachei∈MHSjdo

③Covers(MHSj)0;

④ end for

⑤ for eachei∈HSdo

⑥ if (ei∈MHSj) then

⑦Covers(MHSj)+ +;

⑧ end if

⑨ end for

该方法使用数组保存每个原始的极小冲突集合(MHSj)被当前HS中元素覆盖的情况(行①～④)；对被检测的HS中每个元素的集合覆盖度进行统计，以便后续判断该HS中该元素是否为冗余元素(行⑤～⑨)；然后对被检测的HS中每个元素所覆盖集合度的情况进行统计，根据不同的集合覆盖度情况加以相应的处理(行⑩～).其中行～是对集合覆盖度小于2的元素即非冗余元素进行跳过处理，行～是查找冗余元素并对其从当前待检测碰集中执行删除操作，行～是把对应的冗余元素的相应覆盖的集合的覆盖度进行更新操作，行是输出碰集经过极小化方法后得到的极小碰集.

该方法和以前SSDM的极小化策略相比，其优点是碰集极小化判定时间不会随着极小碰集个数的增加，极小化时间随之急剧增加，而是只与输入的极小冲突集合簇的大小有关，大大提高了极小化求解效率.实验数据结果对比见4.1节.

3 利用SAT求解极小碰集的方法

3.1 将求解碰集问题转换成SAT问题

本节将介绍如何将极小冲突集合簇转换成CNF的形式.

要想把碰集问题转换成SAT问题，首先是如何把要解决的集合形式化表示成SAT问题求解器能够读取和处理的CNF形式，实质上，只要把所有的冲突集合簇表示成CNF形式，然后把每个冲突集合中的元素用SAT中的文字来表示，每个冲突集合用一个子句来表示，举例说明如下:

例2. 以极小冲突集合簇MCS={{1,6},{2,4},{1,2,3},{1,3,5},{2,3,5}}为例，介绍一下如何对极小冲突集合簇进行形式化表示，得到相对应的CNF文件描述.

冲突集合簇(MCS)形式化CNF描述如下：

① p cnf 6 5

② 1 6 0

③ 2 4 0

④ 1 2 3 0

⑤ 1 3 5 0

⑥ 2 3 5 0

上述CNF描述例子语法解释如下：

行①中的“p cnf”是关键字，“6”代表集合变量元素的个数，“5”代表对应的极小冲突集合的个数.行②～⑥中每行是一个极小冲突集合，其中除0以外的数字代表极小冲突集合中存在的元素且均为正，每行的结尾数字0代表极小冲突集合结束符.

碰集的定义要求碰集覆盖所有的极小冲突集合簇，此点和SAT问题中的所有的析取范式都必须为真然后构成一个合取范式为真是相同的.可见碰集问题和SAT问题的实质是集合覆盖问题，只是有些概念的定义范围略有不同，所以可以将一个碰集的求解问题转化为SAT问题进行求解.

3.2 方法核心描述

首先简单介绍一下隔离子句[21]，其定义是将可满足性求解器所得到的解中所有变量的逻辑赋值取反，作为新的子句加入到SAT子句库中.

例3. 如用可满足性求解器得到一个解为

v1,-v2,v3,-v4.

上式表示，当变量v1,v3的逻辑取值为true(1),而变量v2,v4的逻辑取值为false(0)时，输入的合取范式能够被满足.此时，我们将这些变量的逻辑值取反作为它们各自对应文字的逻辑符号，就构成了SAT求解器所需要的隔离子句：

-v1,v2,-v3,v4.

本文SAT-MHS方法法采用的是循环迭代求解方法，该方法主要思想是在调用SAT求解极小碰集的过程中，把之前每次求解的碰集极小化后取反添加到CNF中.屏蔽对该解和非极小解及部分无用搜索空间求解，达到缩减求解空间，提高求解效率.每次求解判断是否为可满足，当不可满足则终止求解.

3.3 SAT-MHS方法实现

算法2. SAT-MHS.

输入：CONFLICT={CF1,CF2,…,CFj,…,CFM};

输出：MHSs.

①Trans_CNF(CONFLICT，CNFs);

② 初始化MarkUNSATISFIABLE；

③MarkIS_SATISFIABLE(CNFs);

④ if(Mark= =UNSATISFIABLE) then

⑤ return;

⑥ else

⑦ while (Mark==SATISFIABLE) do

⑧New_HS=Picosat_Sat(CNFs);

⑨ClauseIS_MHS(New_HS);

⑩MHSs←MHSs∪Clause;

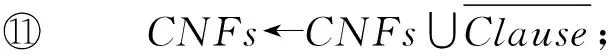
算法2首先把输入极小冲突集合簇转化为SAT求解器能够读取的CNF文件(行①)，初始化可满足性变量Mark(行②).然后首次调用SAT求解器对CNF文件进行可满足性求解并对其值为不可满足时则返回，结束算法(行③～⑤)；否则，把可满足的赋值进行极小化处理得到的极小碰集添加到极小碰集集合簇中，并对求解的极小碰集以取反的隔离子句的形式添加到原始的CNF中，屏蔽掉该极小碰集对应的求解空间(行⑧～).最后对是可满足的CNF不断循环迭代的求解，直到得到不可满足(行⑦～)，结束while循环并得到所有的极小碰集MHSs(行).

下面主要对SAT-MHS方法最关键的DOEC极小化策略举例说明其应用效果.

对于例1中的冲突集合簇对应的HS，假设该方法当前得到碰集{2,3,4,5,6}，如果不使用DOEC极小化策略对其进行处理，而是直接以隔离子句形式将其加入到SAT的CNF文件中，则只是剪枝屏蔽掉了{1,2,3,4,5,6}这一个解，其剪枝效果如图1(a)所示.但如果使用DOEC极小化策略对求解出碰集{2,3,4,5,6}进行极小化处理后得到极小碰集{3,4,6}，然后再把其以隔离子句的形式加入到SAT的CNF文件中，可以从图1(b)中看出其把结点{3,4,6}所应的超集剪枝掉，从而有效地避免了对非碰集和非极小碰集的求解，减少调用SAT求解的次数，使方法更加高效.

4 实验与结果

实验所用的所有实验用例均是随机生成，输入参数有元素个数n、集合簇中集合个数m以及元素在一个集合中出现的概率p.在同一个用例中，所有元素的p均相等，每个集合包含元素的平均个数约等于np.本文使用的实验用例共有4组，分别为30,25,20,15.每组都是包含概率为p的用例，p为从0.05～0.94的19个概率分布数据，每组集合个数都是200.本文所有实验数据均为使用相同参数下独立生成的10个用例所得结果，然后对其取平均值.本文的实验平台均为：系统硬件配置是Intel Core I5-4590 CPU@3.30 Hz x4，8 GB RAM,C语言.

4.1 SSDM和DOEC极小化策略实验结果分析比较

本节使用随机生成测试用例的25和30这2组较难的包含概率为p的用例，p取值从0.20～0.80的14个概率分布数据进行实验，实验数据均为使用相同参数下独立生成的10个用例以SAT-MHS方法为基础进行实验所得结果并对其实验结果取平均值，详细如表1所示.

从表1可以看出,对于元素个数N=25的测试用例，DOEC极小化策略是SSDM极小化策略求解速度的1～40.3倍;而对于N=30的测试用例，DOEC极小化策略是SSDM极小化策略求解速度的21～55.1倍之间，可见DOEC极小化策略对于较大规模测试用例的高效性.除此之外，DOEC极小化策略会随着碰集个数的增多和元素个数的增多，

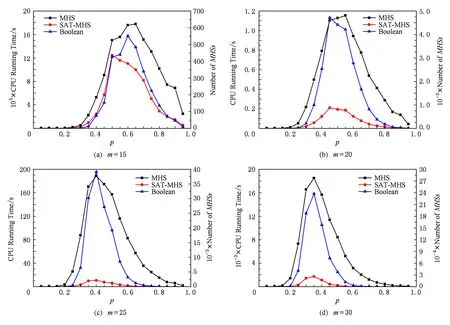
Fig. 2 The performance comparison of SAT-MHS and Boolean图2 SAT-MHS方法与Boolean方法实验结果比较

其求解的效率也会随之增加.所以，DOEC极小化策略会随着待求解问题规模的增大，其求解效率也会随之增加.

4.2 SAT-MHS方法与Boolean方法对比分析

本节使用SAT-MHS方法与目前求解效率较高的Boolean方法进行比较，并给出2种方法在随机生成测试用例的实验结果.

从图2中可以看出，对于元素个数m=15的测试用例，因其碰集个数和元素个数较少，所以其求解耗时较少，但SAT-MHS方法还是略比Boolean方法用时少.对于元素个数较多的用例m=20,25,30,SAT-MHS方法的优势就较为明显.随着所要求解的极小碰集的个数不断增加，SAT-MHS方法的优势越来越明显，求解时间的差距也越来越大，所以对于碰集个数较大的问题其拥有较大优势.尤其对于耗时较长的用例来说，SAT-MHS的求解效率为Boolean方法的30倍左右.不难发现，对比Boolean方法，SAT-MHS方法在耗时越长的测试用例中其优势越明显.

从图3可以看出，对于所需求解的极小碰集的个数较少的测试用例，当两者的求解时间在10-3s以下，SAT-MHS方法的求解时间大于Boolean方法,因为调用SAT求解器需要一些初始化时间;但随着求解规模的增大，当求解时间在10-3～10-2s之间时，可以看出两者的求解时间逐渐接近；当求解时间在10-2～100s之间，SAT-MHS方法的求解效率明显是Boolean方法的3～7倍之间；当求解时间在100～102s之间，其求解效率甚至高达10～20倍；当求解时间在102～104s之间，SAT-MHS方法的求解效率基本是Boolean方法的10倍以上.综合对比图2和图3可以看出，SAT-MHS方法与Boolean方法相比，在求解极小碰集的规模大及复杂性高的问题，其基本求解效率在10倍以上.

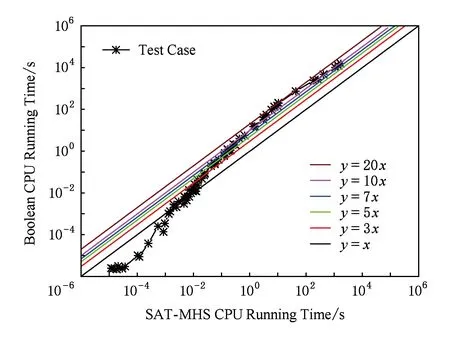
Fig. 3 The comparison results of efficiency between SAT-MHS and Boolean 图3 SAT-MHS方法与Boolean方法实验求解效率比较

此外，从图3可以看出，在求解小规模问题时，Boolean没有初始化过程，而SAT-MHS求解时需要初始化，因此其求解时间比Boolean多些.但当问题规模越大时，产生的碰集个数增多，需要花费大量的时间处理极小化问题，可见SAT-MHS更有优势.

5 总 结

极小碰集在现实生活中有重要的实际应用价值，目前主流完备的碰集极小化策略是SSDM，但其不足是其极小化效率会随着极小碰集的数量增加而使极小化的耗时也随之急剧增多.通过把碰集求解问题转化为SAT问题，然后在DOEC极小化策略的基础上提出了一种新的碰集求解方法SAT-MHS.该极小化策略极小化耗时和已求得的极小碰集规模脱离关系，只与最初的极小冲突集合簇的大小有关，不会随着求解的极小碰集数量的增加而迅速增加.

SAT-MHS方法把极小冲突集合簇转化为SAT求解器能处理的CNF文件，并调用较为成熟的SAT求解器进行循环迭代的碰集求解；每次可满足的文字变量赋值就是SAT求解器求解得到的一个碰集.然后对得到的非极小碰集用DOEC极小化策略进行极小化，并把处理得到的极小碰集以隔离子句的形式添加到CNF文件中，从而屏蔽待搜索求解空间，提高求解效率.与目前求解效率较高的Boolean方法相比，可以看到该方法的高效性，尤其对求解问题规模和碰集个数较多的问题实例，该方法的求解效率至少在10倍以上.未来的工作是使用启发式求解策略[22-24]求解更大规模的极小碰集问题.

[1]Console L, Dressler O. Model-based diagnosis in the real world: Lessons learned and challenges remaining[C]Proc of the 16th Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 1999: 1393-1400

[2]Struss P. Knowledge-based diagnosis: An important challenge and touchstone for AI[C]Proc of the 10th European Conf on Artificial Intelligence. New York: John Wiley & Sons, 1992: 863-873

[3]Hamscher W. Readings in model-based diagnosis[OL]. 1992 [2017-06-17]. http:www.citeulike.orggroup14148article8042710

[4]De Kleer J. Diagnosing multiple persistent and intermittent faults[C]Proc of the 21st Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2009: 733-738

[5]Wang Yiyuan, Yin Minghao, Ouyang Dantong, et al. A novel local search algorithm with configuration checking and scoring mechanism for the setk-covering problem[J]. Int Trans in Operational Research, 2017, 24(6): 1463-1485

[6]Wang Yiyuan,Ouyang Dantong, Zhang Liming, et al. A novel local search for unicost set covering problem using hyperedge configuration checking and weight diversity[J]. Science China Information Sciences, 2017, 60(6): 062103

[7]Reiter R. A theory of diagnosis from first principles[J]. Artificial Intelligence, 1987, 32(1): 57-95

[8]Greiner R, Smith B A, Wilkerson R W. A correction to the algorithm in Reiter’s theory of diagnosis[J]. Artificial Intelligence, 1989, 41(1): 79-88

[9]Wotawa F. A variant of Reiter’s hitting-set algorithm[J]. Information Processing Letters, 2001, 79(1): 45-51

[10]Jiang Yunfei, Lin Li. The computation of hitting sets with Boolean formulas[J]. Chinese Journal of Computers, 2003, 26(8): 919-924 (in Chinese)(姜云飞, 林笠. 用布尔代数方法计算最小碰集[J]. 计算机学报, 2003, 26(8): 919-924)

[11]Ouyang Dantong, Ouyang Jihong, Cheng Xiaochun, et al. A method of computing hitting set in model-based diagnosis[J]. Chinese Journal of Science Instrument, 2004, 25(4): 605-608 (in Chinese)(欧阳丹彤, 欧阳继红, 程晓春, 等. 基于模型诊断中计算碰集的方法[J]. 仪器仪表学报, 2004, 25(4): 605-608)

[12]Zhao Xiangfu, Ouyang Dantong. A method of combing SE-Tree to compute all minimal hitting sets[J]. Progress in Natural Science, 2006, 16(2): 169-174

[13]Chen Xiaomei, Meng Xiaofeng. Qiao Renxiao. Method of computing all minimal hitting set based on BNB-HSSE[J]. Chinese Journal of Science Instrument, 2010, 31(1): 61-67 (in Chinese)(陈晓梅, 孟晓风, 乔仁晓. 基于BNB-HSSE计算全体碰集的方法[J]. 仪器仪表学报, 2010, 31(1): 61-67)

[14]Zhang Liming, Ouyang Dantong, Zeng Hailin. Computing the minimal hitting set based on dynamic maximum degree[J]. Journal of Computer Reach and Development, 2011, 48(2): 209-215 (in Chinese)(张立明, 欧阳丹彤, 曾海林. 基于动态极大度的极小碰集求解方法[J]. 计算机研究与发展, 2011, 48(2): 209-215)

[15]Pill I, Quaritsch T. Optimizations for the Boolean approach to computing minimal hitting sets[C]Proc of the 20th European Conf on Artificial Intelligence. Amsterdam: IOS Press, 2012: 648-653

[16]Wang Yiyuan, Ouyang Dantong, Zhang Liming, et al. A method of computing minimal hitting sets using CSP[J]. Journal of Computer Research and Development, 2015, 52(3): 588-595 (in Chinese)(王艺源, 欧阳丹彤, 张立明, 等. 利用CSP求解极小碰集的方法[J]. 计算机研究与发展, 2015, 52(3): 588-595)

[17]Yang Kun, Bai Hongjun, Ouyang Qi, et al. Finding multiple target optimal intervention in disease-related molecular network[J]. Molecular Systems Biology, 2008, 4(1): 228

[18]Zhou Gan, Feng Wenquan, Jiang Bofeng, et al. Computing minimal hitting set based on immune genetic algorithm[J]. Int Journal of Modelling, Identification and Control, 2014, 21(1): 93-100

[19]Jannach D, Schmitz T, Shchekotykhin K. Parallelized hitting set computation for model-based diagnosis[C]Proc of the 24th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2015: 1503-1510

[20]Zhao Xiangfu, Ouyang Dantong. Deriving all minimal hitting sets based on join relation[J]. IEEE Trans on Systems, Man, and Cybernetics: Systems, 2015, 45(7): 1063-1076

[21]McMillan K L. Applying SAT methods in unbounded symbolic model checking[C]Proc of Conf on Computer Aided Verification. Berlin: Springer, 2002: 250-264

[22]Wang Yiyuan, Cai Shaowei, Yin Minghao. Local search for minimum weight dominating set with two-level configuration checking and frequency based scoring function[J]. Journal of Artificial Intelligence Research, 2017, 58(1): 267-295

[23]Wang Yiyuan, Cai Shaowei, Yin Minghao. Two efficient local search algorithms for maximum weight clique problem[C]Proc of the 13th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2016: 805-811

WangRongquan, born in 1992. Master candidate at Jilin University. His main research interests include model-based diagnosis, SAT problem and automated reasoning.

OuyangDantong, born in 1968. Professor and PhD supervisor of Jilin University. Senior member of CCF. Her main research interests include model-based diagnosis, model checking and automated reasoning (ouyangdantong@163.com).

WangYiyuan, born in 1988. PhD candidate at Jilin University. His main research interests include model-based diagnosis, SAT problem and automated reasoning (yiyuanwangjlu@126.com).

LiuSiguang, born in 1988. Master candidate at Jilin University.His main research interests include model-based diagnosis,SAT problem and automated reasoning (lsgmliss@163.com).

ZhangLiming, born in 1980. PhD, post-doctor in Jilin University. His main research interests include model-based diagnosis,SAT problem and automated reasoning.