多速率分布式预测控制及其在热连轧活套系统中的应用

张晓东 高绍姝 刘新平

随着多智能体系统的广泛应用,分布式预测控制成为研究的热点[1−4].采用分布式控制方式能够把整个系统的优化问题分散到各个子系统中去解决,适用于各子系统间动态独立的对象.基于预测控制原理,学者们提出了多种分布式控制控制策略.如子系统控制律同步获取、同步实施[5−6];顺序获取、同步实施[7−8]以及迭代方式获取、同步实施[9]等方式.热连轧活套系统是具有串联结构的多智能体控制系统.研究人员在热连轧活套系统控制器的设计方面主要采用分散式控制策略,针对单机架的多输入多输出活套系统设计控制器[10].如采用滑膜控制、鲁棒控制、模糊控制、预测控制等获得了较好的控制效果.由于活套高度与张力控制系统具有强耦合特性,增加了控制器设计的难度.其中文献[11]采用多通路控制策略[12−13],活套高度和张力系统交互更新控制律,对子系统之间的耦合影响具有较好的抑制效果,并建立了活套关联系统模型,在设计单机架控制器的时候,考虑了下游机架轧制速度的影响,提高了活套系统的控制性能.但是,如果采用同步更新控制策略,下游机架轧制速度更新的同时会对上游机架的张力系统产生影响.整个活套系统的稳定性及协调性有待进一步提高.本文针对具有串联结构的多智能体控制系统,提出一类多速率分布式预测控制策略,并将该算法应用到热连轧活套控制系统,提高系统的稳定性和协调性,通过仿真实验验证了该方法的有效性和可行性.

1 多速率分布式预测控制策略

通常情况下,基于预测控制原理的分布式控制采用同步更新控制律的方式.但是,对于相互耦合影响的多智能体系统,在控制律同步更新的同时也会对其他子系统产生扰动影响,这种扰动影响难以消除,尤其是对信息有向传输的串联结构的多智能体系统,会随着信息的逐级传输影响整个系统的稳定性,降低智能体之间的协调性能.基于此,本文提出多速率分布式预测控制策略,如图1所示.设有M个智能体,基于预测控制原理,实施多速率异步控制策略.即:在一个输出采样周期T内,顺序获得控制序列ui(k+j)后开始新的循环.其中i={1,···,M},j={0,···,Nu− 1}.针对第i个子系统,在一个周期T内,生成ui(k),ui(k+1),···,ui(k+Nu−1)共Nu个控制律,控制律更新周期为T/M.其中Nu=M为控制时域,L是最大预测时域.令其中l={Nu,···,L},即在Nu步后控制律不变化.控制信息和输出信息从第i个智能体向第i+1个智能体传递.

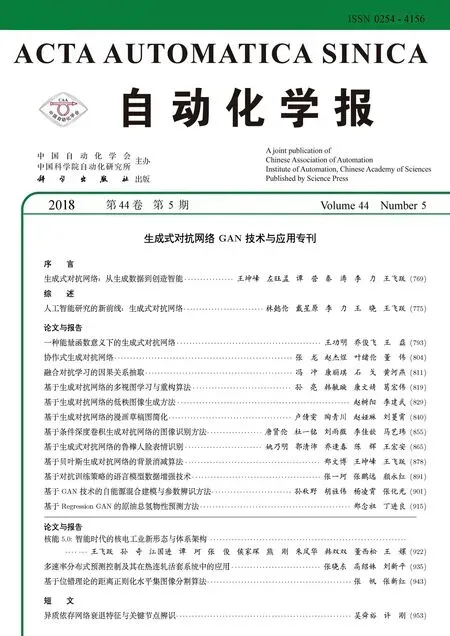
考虑如下离散时不变系统模型[14]

其中,xi,yi和ui分别是第i个系统的状态、输入和输出向量,Ai,Bi,Ci和Di是相应维数的矩阵.基于多速率控制策略,系统输出的采样周期设为T,控制输入信号的采样周期为T/M.

我们定义如下表示形式

基于提升技术,控制信号可以表示为

如果M=2,则控制信号表示为

根据式(1)和(2),多速率系统模型可以表示为

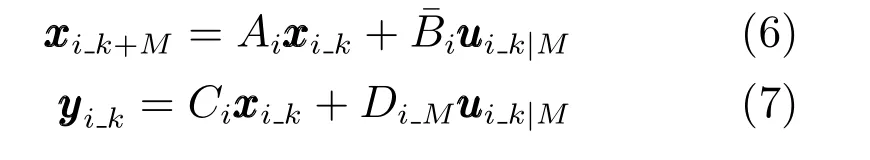
其中,基于提升技术上述方程可以改写为

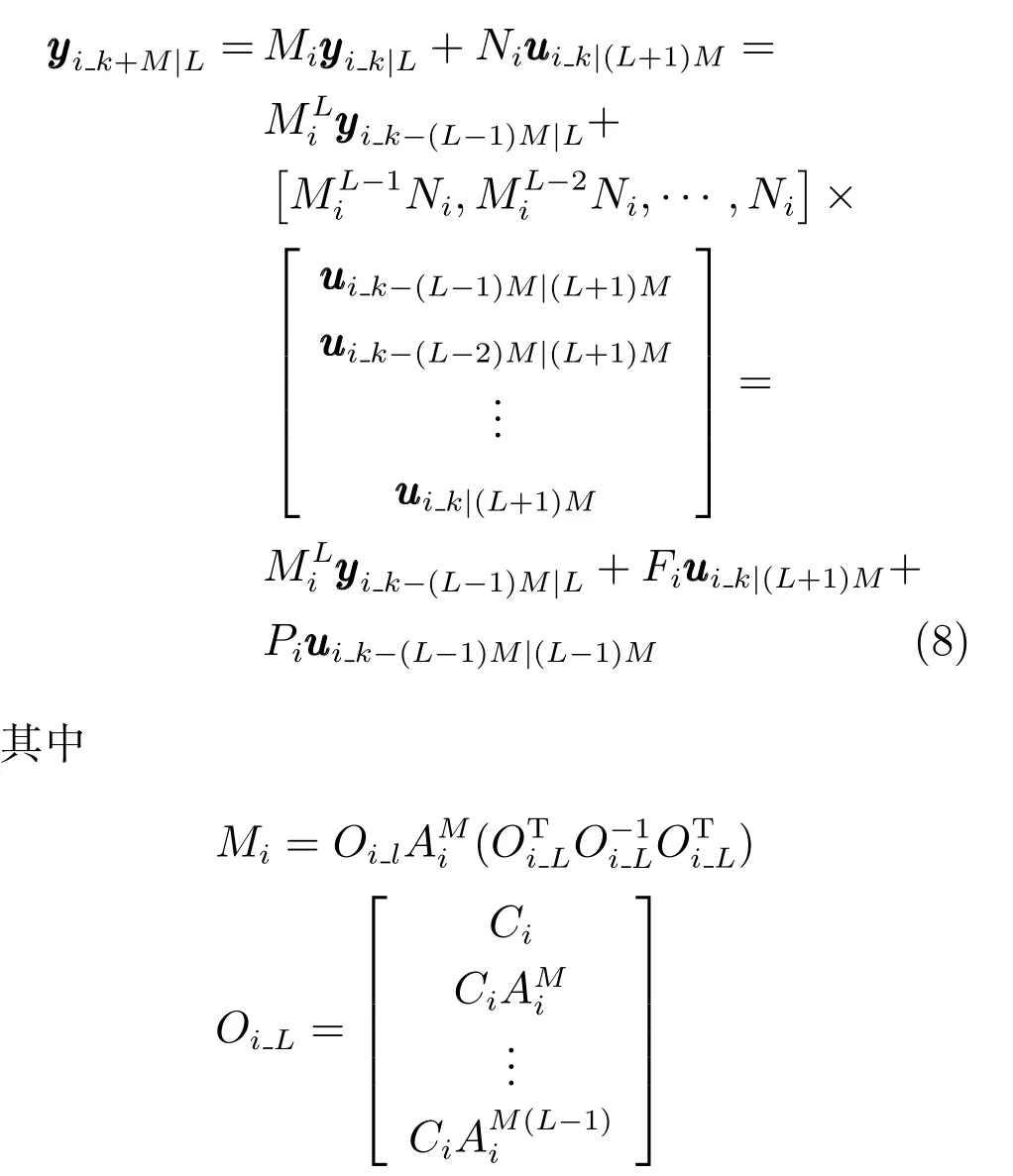
图1 分布式预测控制方框图Fig.1The diagram of distributed predictive control strategy

基于本文提出的多速率分布式控制策略,在k时刻每一个智能体的控制序列分为两部分.如图1所示,一部分为k−1时刻求解的控制律,可以视为已知量,另一部分为当前k时刻求解的控制律.

定义如下矩阵

其中,r为控制输入的维数.

控制律可以表示为

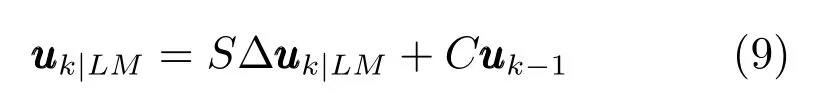
因此输入输出方程(8)可以写为

其中,通过优化如下目标函数求解

其中,ri为参考输出,λi>0为给定的常数.

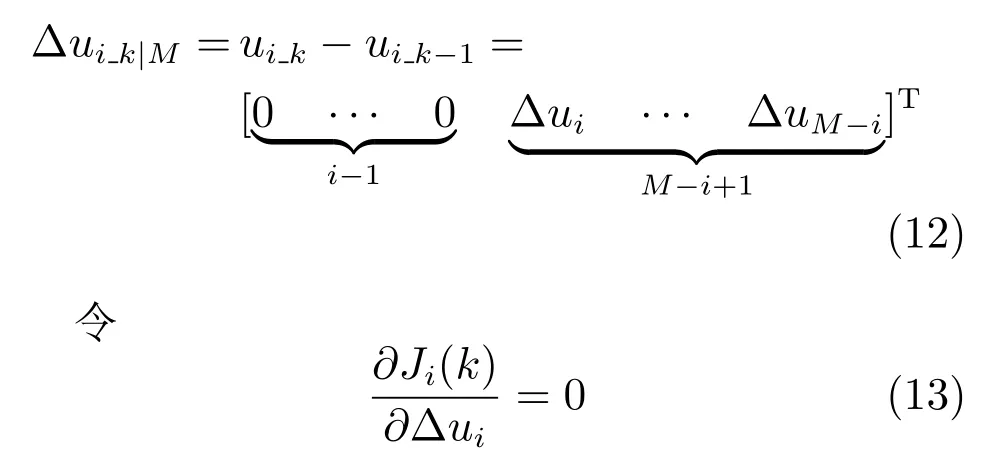
求得k时刻控制律

基于信息有向传输的串联结构的多智能体系统,由于采用多速率异步更新控制策略,能够获得相关联子系统的输入和输出信息对其产生的耦合影响,从而进行有效补偿,提高控制性能.

2 稳定性分析

定理1.在不考虑约束的情况下,如果第i个子系统的特征多项式

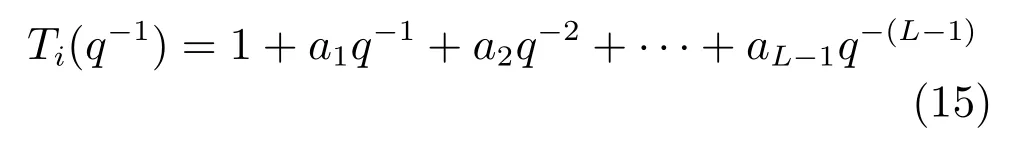
零点均在单位圆内,其中则基于优化性能指标(11)获得的控制律(12)能够使闭环系统(8)稳定.

证明.将式(12)代入到式(8)中,可得到如下方程.

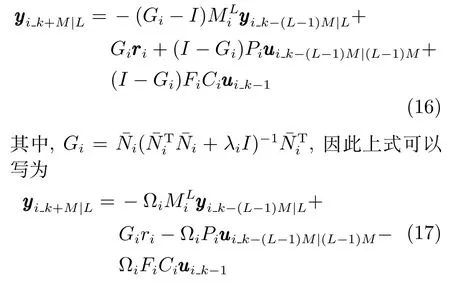
其中,Ωi=[Gi−I](1,:).引入后移算子q−1,上述方程等式右侧可写为

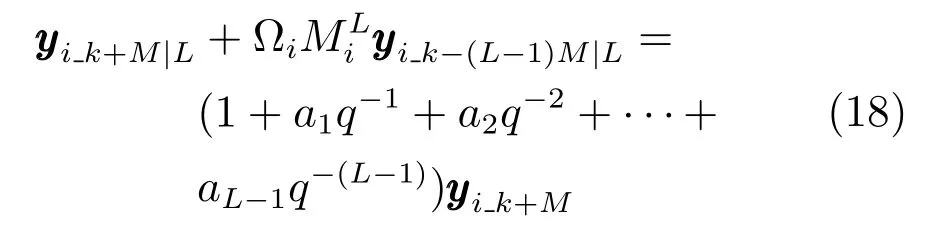
因此,如果特征多项式(15)的所有零点均在单位圆内,则闭环系统稳定.

3 热连轧活套系统模型

热连轧系统一般是由6∼7台机架组成的,活套安装在机架中间,活套系统示意图如图2所示.活套系统通过轧制速度Vi调整张力τi,通过电机电流ii调整活套角度θi,使得活套系统保持恒定的微张力,提高产品质量.从图2中能够看出第i机架活套张力同时受到第i和i+1机架轧制速度的影响.

图2 活套系统示意图Fig.2 Con figuration of looper systems

基于热连轧上、下游机架的关联特性,考虑下游轧机轧制速度对上游机架张力控制的影响,建立热连轧活套系统的关联模型[13].

活套高度系统模型

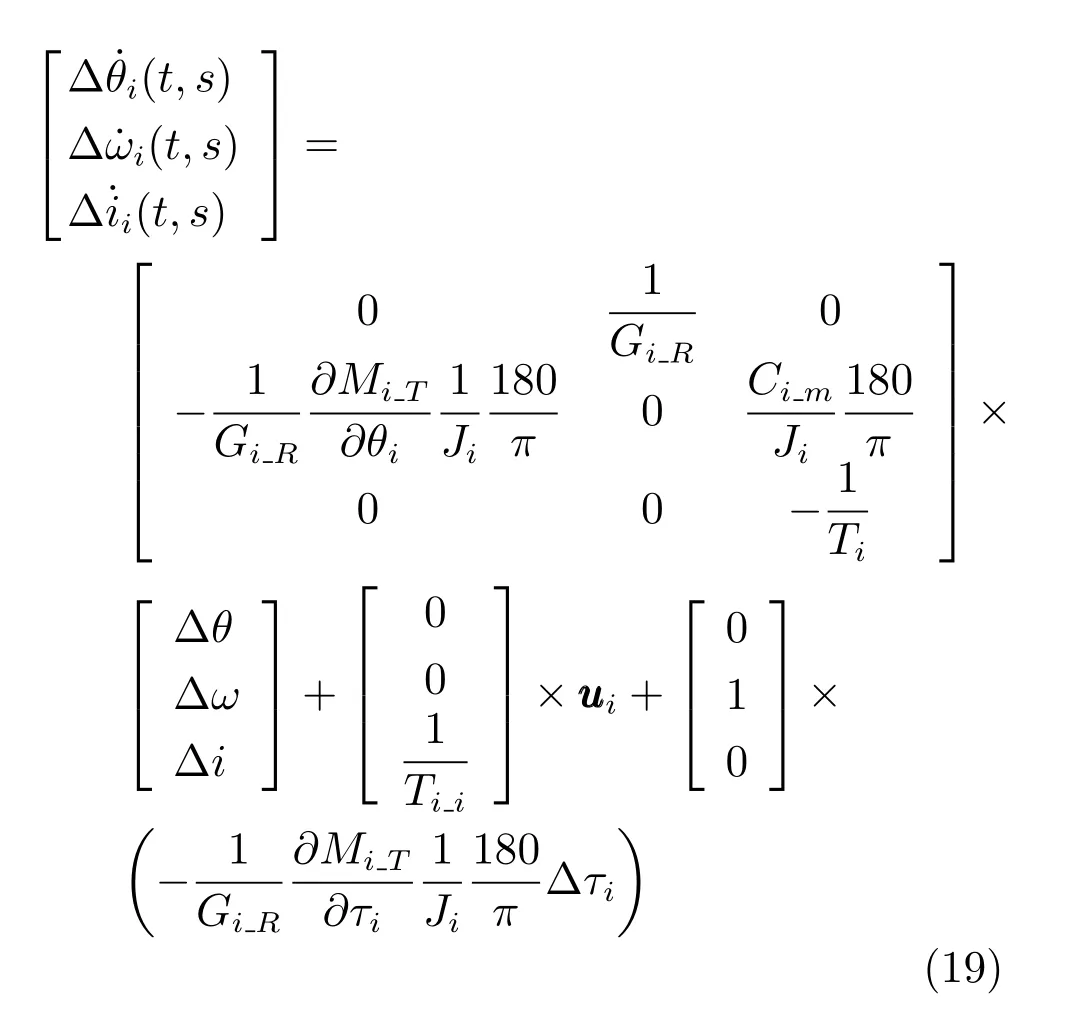
活套张力关联系统模型

其中,ωi为活套角速度,fi和βi分别为第i机架的后滑系数和第i+1机架的前滑系数.其他参数说明可以参考文献[13]的描述.基于异步更新控制策略,在求解第i+1台机架轧制速度后保持不变,顺序求解第i机架的轧制速度时,能够充分考虑第i+1机架的轧制速度变化对当前活套张力系统的影响,从而提高系统的稳定性和控制性能.

4 仿真实例

根据某热连轧厂轧机活套实际参数[15].

活套张力系统的控制输入采样时间为4ms,离散化后得到活套系统的参数为

其中,为活套高度系统参数以及初始条件,和为活套张力系统参数及初始条件.令L=2和λ=1,控制时域和预测时域相同.假设热连轧活套系统都具有相同的控制模型,选取第3,4,5,6活套张力控制系统基进行仿真实验.

1)在初始条件的作用下,基于串联结构的活套系统,下游机架轧制速度变化对上游机架张力系统的影响是逐步增强的.与多速率同步更新控制策略相比较(基于优化性能指标(11)求解控制律),仿真结果如图3(a)和(b)所示.采用异步更新控制方式能够预知关联子系统的扰动进行补偿,控制律变化幅度相对较小,从而提高活套张力系统的稳定性.而采用同步更新的控制方式,第i+1机架控制律会直接作用在第i机架 ∆ui(k)上,使得第i机架当前的控制律变为从而影响系统的稳定性和控制性能.

图3 控制器同步更新与异步更新比较Fig.3The comparison between simultaneous control and asynchronous control

2)对比同步更新控制器方式(单机架活套系统的控制律更新周期与输出周期都为T/M),基于式(1)、(2)和优化性能指标(11)(式(11)中令M=1),求解控制律.仿真结果如图仿真结果如图4(a)∼(c)所示.从仿真结果可以看出,多速率异步更新控制方式与快采样同步更新控制方式的具有相近的控制性能,但能够减小计算量,减轻计算负担.

当第5个机架轧制速度产生一个幅值为1的脉冲扰动时,其活套张力系统响应输出如图5(a)∼(c)所示.采用异步更新的多速率控制策略能够补偿外部扰动对相邻子系统的耦合影响,提高扰动抑制性能.

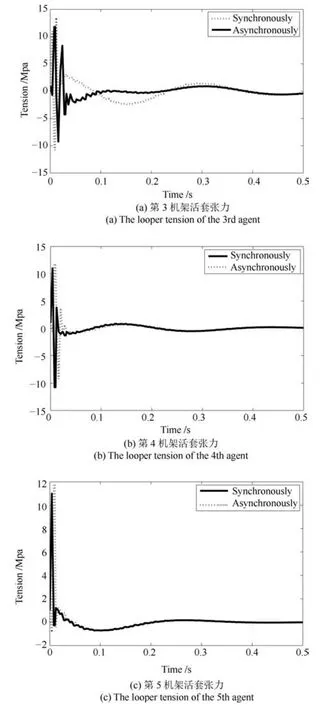
图4 快采样更新与异步更新比较Fig.4 The comparison between fast-sample control and asynchronous control

3)对比同步更新控制器方式(单机架活套系统的控制律更新周期与输出周期都为T),基于式 (1)、(2)和优化性能指标 (11)(式 (11)中令M=1),与多速率异步控制方式相比较,仿真结果如图6(a)∼(d)所示.从仿真结果可以看出采用多速率异步更新方式能够明显地改善系统的控制性能.

图5 扰动情况下快采样更新与异步更新比较Fig.5 The comparison between fast-sample control and asynchronous control with disturbance

5 结论

针对串联结构的多智能体系统,提出一类多速率分布式控制策略.利用信息的有向传递,顺序更新子系统的控制律,能够有效地补偿智能体之间的耦合影响,提高智能体之间的协调性和稳定性,减轻计算负担,并给出了系统稳定性的充分条件.通过热连轧活套张力系统的仿真实验表明,该控制策略具有较好的控制效果.

图6 慢采样更新与异步更新比较Fig.6 The comparison between slow-sample control and asynchronous control with disturbance

1 Conte C,Jones C N,Morari M,Zeilinger M N.Distributed synthesis and stability of cooperative distributed model predictive control for linear systems.Automatica,2016,69:117−125

2 Li H P,Yan W S.Receding horizon control based consensus scheme in general linear multi-agent systems.Automatica,2015,56:12−18

3 Yang Hui,Zhang Fang,Zhang Kun-Peng,Li Zhong-Qi,Fu Ya-Ting.Predictive control using a distributed model for electric multiple unit.Acta Automatica Sinica,2014,40(9):1912−1921(杨辉,张芳,张坤鹏,李中奇,付雅婷.基于分布式模型的动车组预测控制方法.自动化学报,2014,40(9):1912−1921)

4 Cheng Z M,Zhang H T,Fan M C,Chen G R.Distributed consensus of multi-agent systems with input constraints:a model predictive control approach.IEEE Transactions on Circuits and Systems I:Regular Papers,2015,62(3):825−834

5 Wang P,Ding B C.Distributed RHC for tracking and formation of nonholonomic multi-vehicle systems.IEEE Transactions on Automatic Control,2014,59(6):1439−1453

6 Hengster-Movric K,Lewis F L,Sebek M.Distributed static output-feedback control for state synchronization in networks of identical LTI systems.Automatica,2015,53:282−290

7 Richards A,How J P.Robust distributed model predictive control.International Journal of Control,2007,80(9):1517−1531

8 Richards A,How J.Decentralized model predictive control of cooperating UAVs.In:Proceeding of the 43rd IEEE Conference on Decision and Control.Nassau,Bahamas,USA:IEEE,2004,4:4286−4291

9 Kuwata Y,How J P.Cooperative distributed robust trajectory optimization using receding horizon MILP.IEEE Transactions on Control Systems Technology,2011,19(2):423−431

10 Choi I S,Rossiter J A,Fleming P J.Looper and tension control in hot rolling mills:a survey.Journal of Process Control,2007,17(6):509−521

11 Zhang Xiao-Dong,Yao Xiao-Lan,Wu Qing-He.Modeling and receding-horizon control for looper-interconnected systems.Control Theory&Applications,2011,28(12):1797−1802(张晓东,姚小兰,伍清河.活套关联系统建模及滚动时域控制.控制理论与应用,2011,28(12):1797−1802)

12 Ling K V,Ho W K,Wu B F,Lo A,Yan H.Multiplexed MPC for multizone thermal processing in semiconductor manufacturing.IEEE Transactions on Control Systems Technology,2010,18(6):1371−1380

13 Ling K V,Ho W K,Feng Y,Wu B F.Integral-square-error performance of multiplexed model predictive control.IEEE Transactions on Industrial Informatics,2011,7(2):196−203

14 Wang X R,Huang B,Chen T W.Multirate minimum variance control design and control performance assessment:a data-driven subspace approach.IEEE Transactions on Control Systems Technology,2007,15(1):65−74

15 Fu Jian.Application Study on Modern Robust Control Theory and Integrated Control in Hot Strip Rolling[Ph.D.dissertation],University of Science and Technology Beijing,China,2006.(傅剑.现代鲁棒控制理论应用研究与热连轧综合控制[博士学位论文],北京科技大学,中国,2006.)