“立”就给力

李源

画线段图可以使复杂问题简单化、抽象问题具体化，从而达到优化解题的目的。教师在教学中常常用画线段图的方法引导学生分析数量关系，找到解题的突破口。尤其是在解决有关倍数问题（和倍、差倍、和差等）时，用线段分别表示题中的一倍数和几倍数后，再找出这两数之间的和或者差，解题思路就非常清晰了。但遇到稍微复杂的情况，画普通的线段图作用往往不明显，甚至画了图后，学生依然无从下手。如何让线段图发挥更大的效能呢？我在教学中尝试画立式线段图，效果还不错。

例：有甲、乙两桶油，甲桶油的重量是乙桶油的5倍，如果每桶分别倒入48千克的油，那么甲桶油的重量是乙桶油的2倍，甲、乙两桶油原来各多少千克？

常规画图：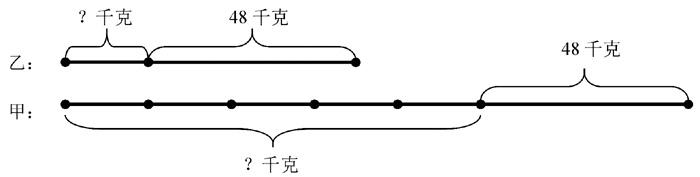

分析：面对上面的线段图，一般的孩子仍然无所适从，找不到突破口，发挥不了线段图的“扶梯”作用。如果改变线段图的形式，将线段图“立”起来呢？就像旧楼改造一样，将爬梯改成直升梯，线段图直观形象的效果就凸显出来了。

立式线段图：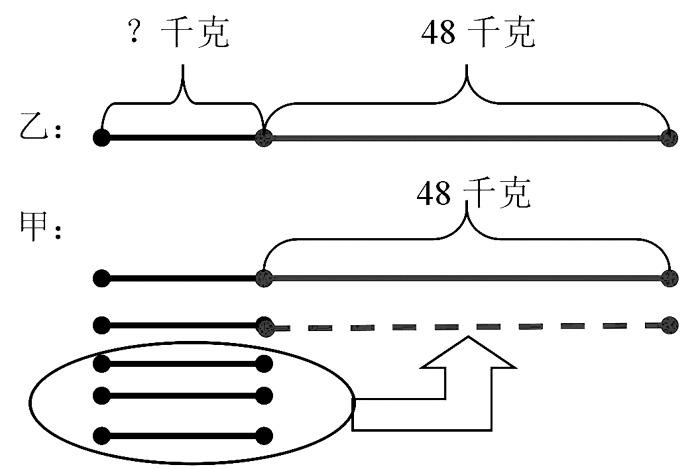

48÷（5-2）=16（千克）———原来乙的重量

16×5=80（千克）———原来甲的重量

除了在解决倍数问题中可以利用立式线段图，解决盈亏问题同样可以采用。

例：用一根绳子测量井的深度，如果绳子折成两折时，多4米；如果绳子折成四折时，差3米，问绳子有多长？井有多深？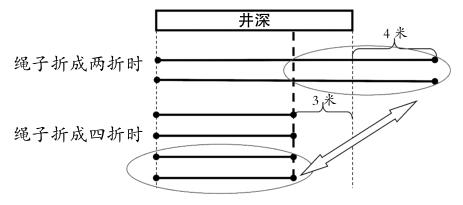

分析：从图中可以清楚地看出，将绳子折成兩折时，每折绳子对齐折成四折时的每段“斩断”，两个圆圈里的绳子长度对应相等。

（4+3）×2÷（4-2）=7（米）———绳子折成四折时一段的长度

7+3=10（米）———井深

7×4=28（米）———绳子的长度

由此可见，立式线段图能清晰地将题中蕴含的数量关系形象、直观地呈现出来，有利于启迪学生的思维，帮助学生轻松解题。

（作者单位：株洲市天元区白鹤小学）