平移不变小波变换在脉搏波去噪中的应用

王泰琨，张海英，张以涛，张 俊，耿兴光

(1.中国科学院微电子研究所 健康电子研发中心，北京 100029；2. 中科院物联网中心，江苏 无锡 214000；3.新一代通信射频芯片技术北京市重点实验室，北京 100029；4.中国科学院大学 微电子学院，北京 101400)

0 引言

“脉搏波”可以理解为“动脉血管搏动引起的皮肤表面可检测到的波动”，即心脏的搏动沿着动脉血管和血流向外周进行传播，从而引起的一种波动的信号，其频率或周期反映了人体多个方面的生理情况。研究表明，脉搏波的信号具有一些较为明显的特征，并且这些特征与心血管系统之间具有十分密切的联系[1]，一直以来，无论是国内还是国外医学界，中医理论还是西医理论，都十分重视脉搏波信号特征中所反映的人体的生理病理信息，并将其列为临床预防、诊断和治疗疾病的检查手段之一。脉搏波是一种异常微弱且不平稳的生理信号, 非常容易受到各方面因素的影响。影响的因素主要包括动脉血管的管壁弹性、管口直径大小、血管壁厚度和血液的粘稠度(包括密度和粘性)。医护工作人员根据这些内在联系，将得到的脉搏波信号进行“抽丝剥茧”，依靠这些信号来为患者诊断。除上述影响因素之外，脉搏波的信号也很容易受到工频噪声干扰的影响，这些噪声引起的干扰使脉搏波信号不能够准确地反映患者的生理病理状况，为医生的诊断带来一定程度的影响。综上，为使脉搏波信号可以反映受检人员的真实情况，在测量和记录表面肌电信号时应当尽量消除噪声干扰的影响[2]。

在信号分析处理领域中，傅里叶变换一直处于遥遥领先的地位，其在平稳信号分析中的表现十分出色，是处理平稳信号的有效手段。但是对于脉搏波这种非平稳信号而言，傅里叶分析显然并不能继续发挥其优良性能。随着科学技术的革新，近十来年人们在傅里叶分析的基础之上逐步研究出一种适用于非平稳信号的分析方法——小波分析法。到目前为止，小波分析理论在信号分析处理的领域已经得到了大范围的认可。小波分析理论常用的去噪方法主要包括传统的硬阈值小波去噪法和软阈值小波去噪法。其中，硬阈值小波去噪法能够很好地保留脉搏波信号中细节的特征性，但是由于脉搏波信号是一种非平稳信号，信号的重构会出现不连续性，因此利用这种传统方法处理会在信号的奇异点出现一种上下跳动的现象，也就是伪吉布斯现象[3]。平滑处理是数据分析中一类重要和常用方法。平滑处理的目的在于既保留资料中的主要有用信号，又消除或削弱随机误差[4]。而软阈值小波去噪法利用这种思想虽然能够克服硬阈值小波去噪法的缺点，抑制伪吉布斯现象，但是会使信号过度平滑，也不利于脉搏波信号提取后的再处理分析。

本文拟采取一种全新的小波去噪方法——平移不变的新阈值小波去噪法。该方法可以在有效抑制伪吉布斯现象的同时提高信噪比。平移不变的新阈值小波去噪法是对传统小波变换在脉搏波信号处理领域的探索改进和应用，本文将通过仿真实验、分析整理、归纳对比等方法来说明该算法的实用性和先进性。

1 小波阈值去噪的基本原理和方法

1.1 小波除噪的基本原理

小波分析和傅里叶分析虽然同根同源但是仍然存在着较大的差异：傅里叶分析是处理平稳信号的常用方法，小波分析则更适用于处理非平稳信号。小波分析通过对空间和频率做局部的变换来提取信号中的不稳定信息，该分析方法处理的核心是对信号进行平移和压缩，因此可以对信号进行更多尺度的分析。

小波分析方法去除信号噪声的流程具体如下：

(1)小波变换：选择一种适合的小波基及分解层次，并对含有白噪声的原始信号进行逐级分解，从而得到各级的小波系数数列。

(2)小波系数量化处理：预先设置一个阈值处理函数，并通过该处理函数将预估的噪声部分进行处理，得到一组新的小波系数数列。

(3)小波重构：对逐级分解得到的小波系数的数列进行小波逆变换，继而得到去噪后的脉搏波信号。

1.2 传统阈值处理函数

如何选取合适的阈值和如何量化处理阈值是阈值去噪的两大核心步骤。去噪处理后的波形应该尽可能地保留原始信号的细节特征。早在20世纪末，Donoho等人就以小波变换的思想为研究基础进一步优化了去噪方法，提出了小波变换硬阈值和软阈值的去噪方法[5-6]。硬、软函数分别如式(1)、式(2)所示：

(1)

(2)

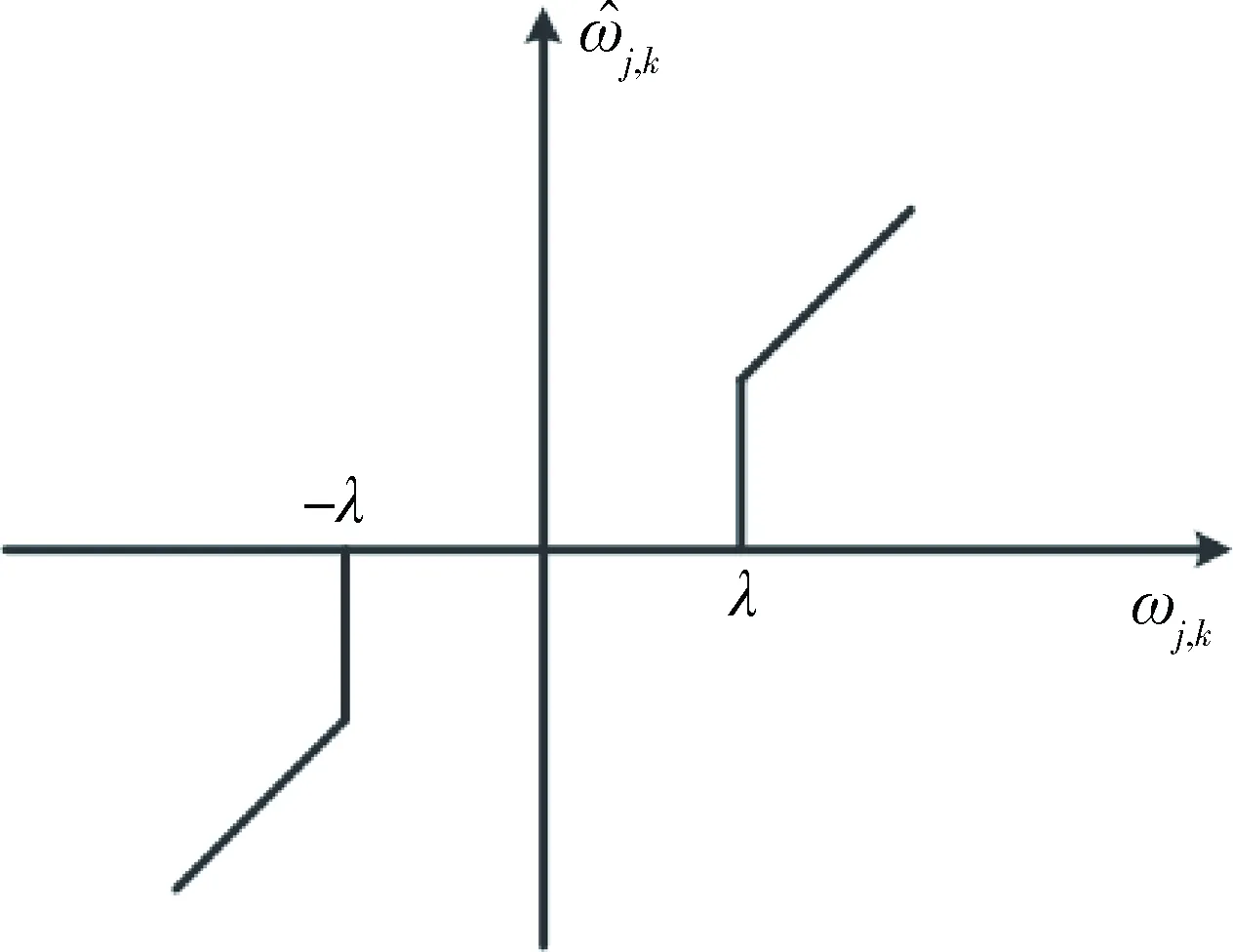
图1 硬阈值函数

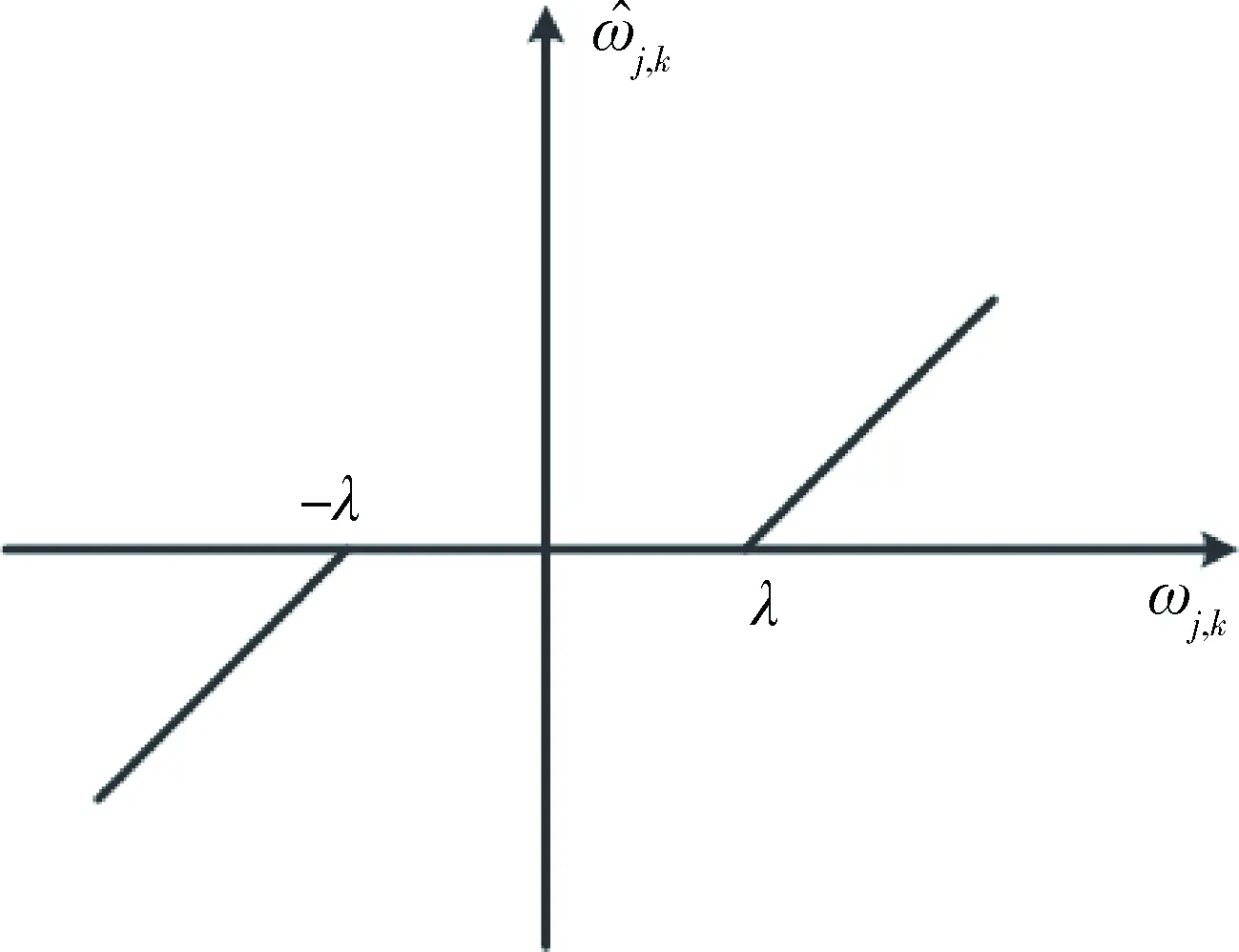
图2 软阈值函数

如图1所示，硬阈值去噪得到的信息更多保留了原始的信号数据，如更多原始信号数据的尖峰信息，但是同时也存在连续性差的缺点。连续性差会使硬阈值函数在某些点上出现间断，而且在去噪重构后也会使信号产生吉布斯振荡。这种震荡现象在原始的信号数据中并不存在，是在人为的去噪处理过程中引入的外部干扰。图2中软阈值去噪时虽然得到的信号相对连续平滑，但当|ωj,k|≥λ时，并不能体现出信号的实际数据，即估计值与实际值之间会存在一个恒定不变的差值[7]。

1.3 新阈值处理函数

为了克服上述两种阈值的缺陷，在保证去噪时小波系数在小波空间的连续性的同时尽可能地降低小波系数的偏差，本文提出了一种新的阈值函数，如式(3)所示:

(3)

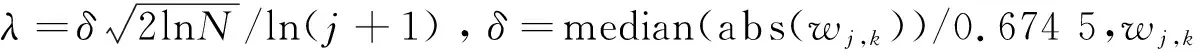
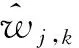
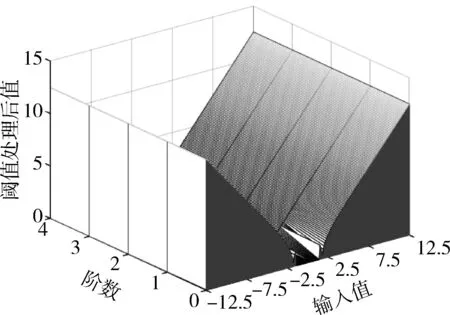
图3 新阈值函数

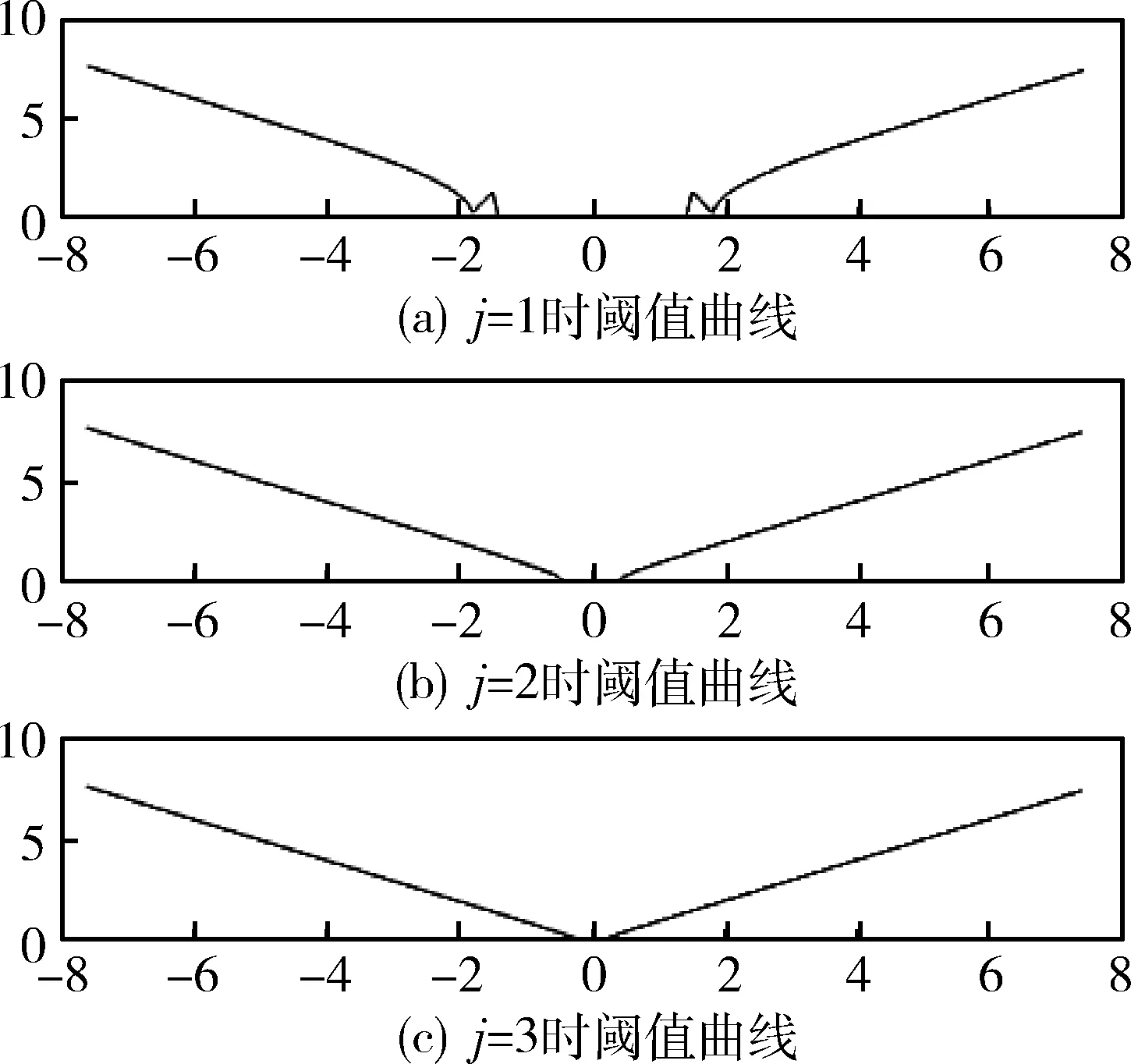
图4 新阈值函数(j=1,2,3)

2 平移不变小波变换

本文提出的平移不变小波去噪法是以阈值去噪法为基础进一步优化算法得来的，可以很好地抑制伪吉布斯现象。平移不变小波变换的基本原理是在一定范围内将噪声信号进行多次的循环平移，完成噪声处理后，再进行逆循环平移对结果平均。平移不变小波去噪的具体步骤如下[8]：

(1)对时域信号x平移h个单位：

Sh(x)=x(t+h)

(4)

(2)对第一次循环平移后得到的信号做离散小波变换处理，并对阈值进行去噪处理。所得的重构信号为：

M1(x)=S-h(T(Sh(x)))

(5)

(3)再对每次步骤(2)所得的结果进行平均处理。无限次(N)循环平移的平移不变小波去噪可以用下式来表达：

(6)

其中Fi(x)为第i个点进行平移不变小波变换去噪处理后的计算值。由上述公式可以看到，该值是对前面所有的去噪结果进行平均处理后得到的。循环平移的处理方法可以用于解决复杂信号(包含多个奇异点)的去噪。

3 实验与结果

3.1 降噪效果评价标准

基于平移不变量的新阈值去噪方法在脉搏波信号去噪中的表现良好，为了将这种优势描述得更加具体，本文将采用常用的信噪比(SNR)和均方根误差(RMSE)两个参数为基准进行评价。引入的信噪比和均方根误差的定义如下：

(7)

(8)

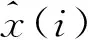
3.2 仿真实验及性能分析

基于脉搏波信号的变化特点，本文采用MIMIC II Waveform DB v2数据库，截取a44579m的一段较为纯净的长1 h的信号，去除基线后作为原信号，采样率为125 Hz，分别添加信噪比为1 dB、3 dB、5 dB、7 dB的高斯白噪声进行混合，作为几种去噪方法的源信号。实验的应用平台为MATLAB R2016b, 选用db6小波，分解层数为4层，对比硬阈值去噪、软阈值去噪、采用本文的新阈值去噪和采用新阈值同时采用平移时不变小波去噪4种方法的去噪效果，结果如图5所示。

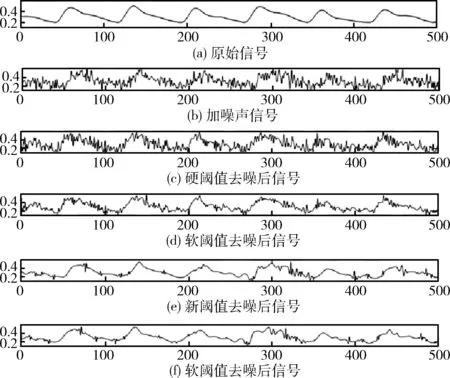
图5 4种方法去噪后的信号SNR对比

如图5所示，在加入SNR为5 dB的高斯白噪声情况下，新阈值方法去噪后信号明显要比硬阈值和软阈值方法清晰且与原信号的时序特征更加相近。

表1和表2是计算4种去噪方法的信噪比和均方根误差。

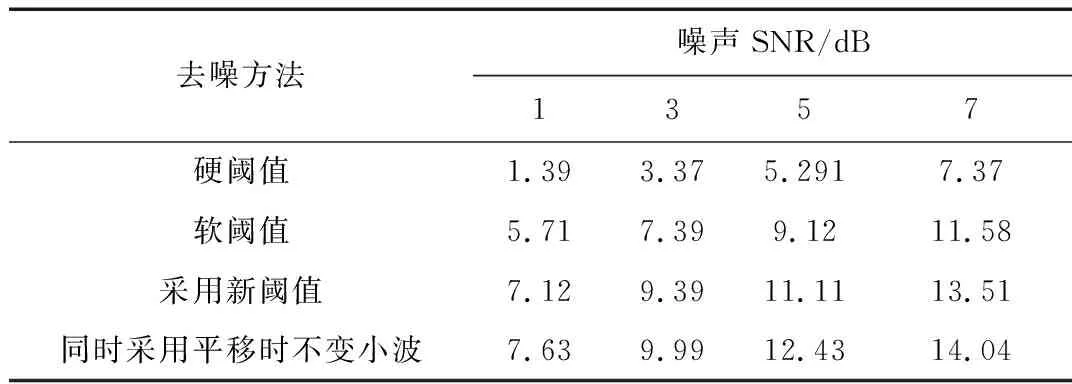
表1 4种方法去噪后的信号SNR对比

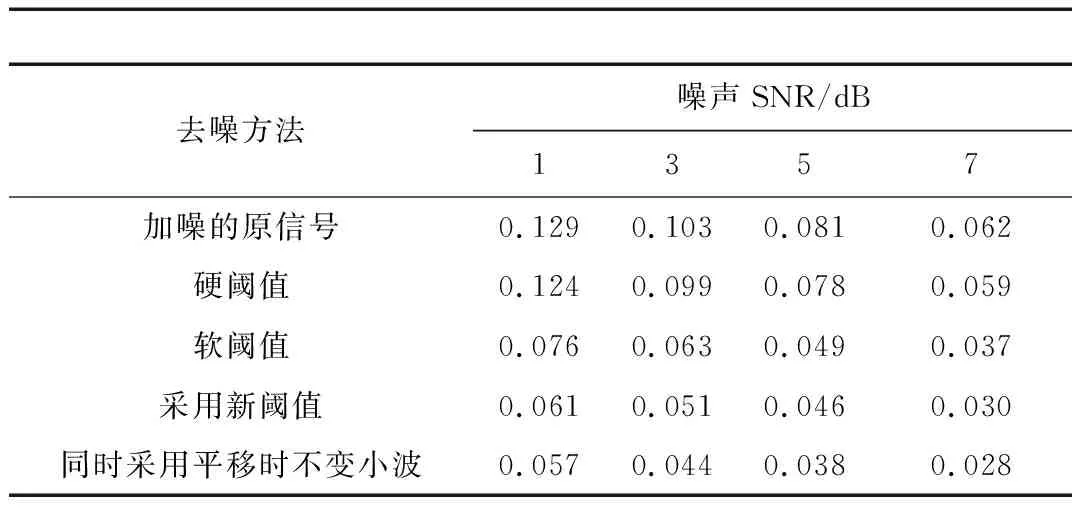
表2 4种方法去噪后的信号和原信号RMSE对比

表1表2印证了前文结论，证明脉搏波信号在高斯白噪声SNR为1～7的情况下，硬阈值、软阈值、本文所述新阈值、新阈值结合平移时不变小波的去噪效果是依次递增的，在噪声SNR=7 dB时，采用平移时不变小波的新阈值小波去噪效果理论上甚至可以达到14 dB。在信噪比很低的情况下，新阈值和结合平移时不变方法能更大程度地还原信号。

3.3 平移时不变小波的去除伪吉布斯现象效果

应用本文所述的新阈值结合平移时不变小波去噪方法，放大图5的某一片段结果，如图6所示。

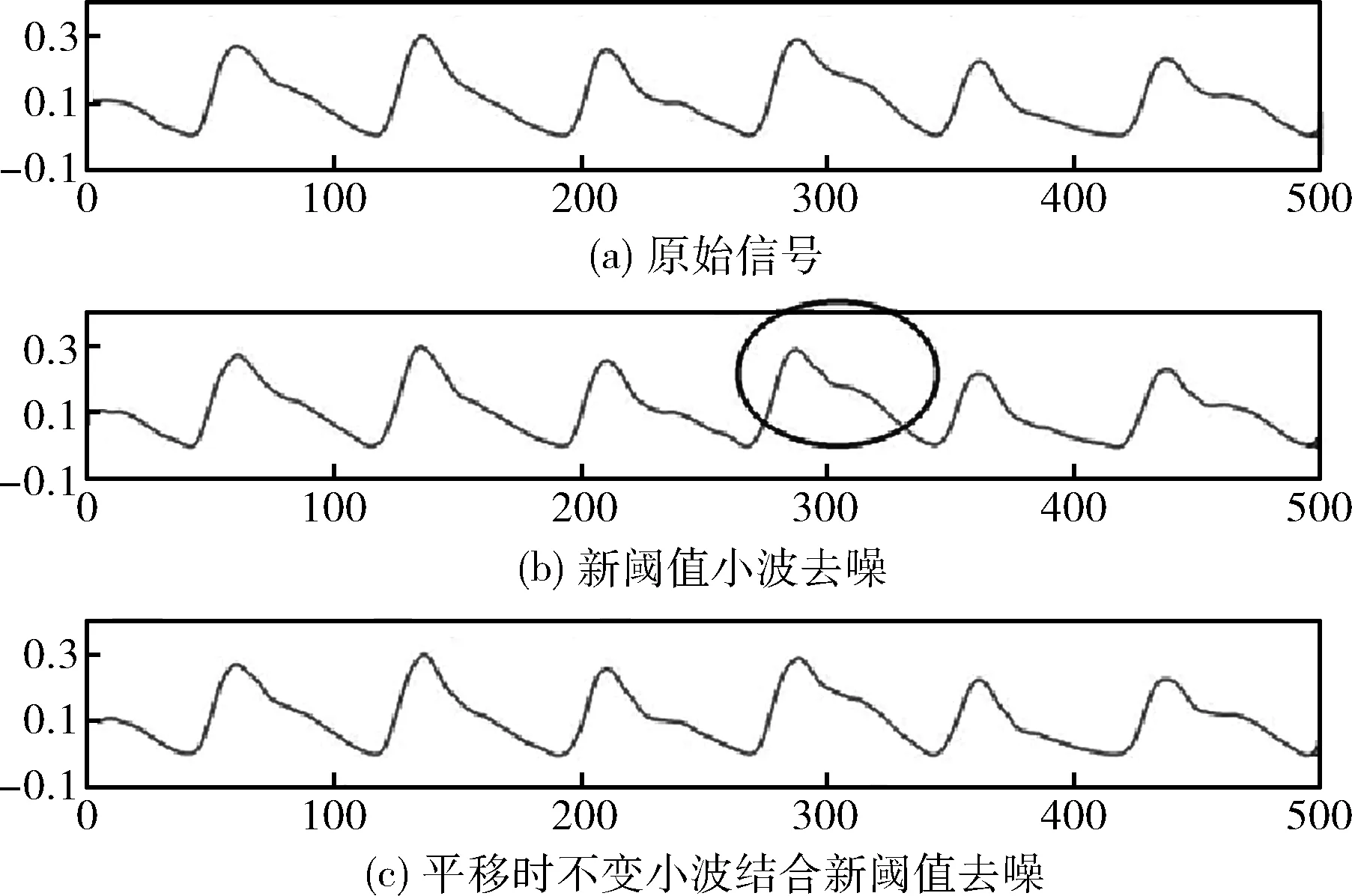
图6 平移时不变小波的去除伪吉布斯现象效果

如图6圈中的部分所示，平移时不变小波平移多次的小波去噪结果要比不平移的仅新阈值去噪结果平滑，解决了图5新阈值小波去噪信号中的在脉搏波二次谐波附近处理所造成的伪吉布斯现象。这对后续脉搏波的特征点识别、周期划分、特征识别有着重要意义。

4 结论

综上所述，较传统方法而言，本文提出的平移不变小波去噪法更适用于脉搏波信号的去噪处理。改进的新阈值平移不变小波变换方法能够较好地弥补传统小波阈值去噪方法中的不足之处。该方法摒弃了传统的阈值函数，使用了新的小波阈值函数，并在此基础上进一步结合了平移不变小波变换，不仅使去噪效果大大提高，而且能够有效抑制伪吉布斯现象。

此外，通过仿真实验，进一步验证了将平移不变小波变换应用于脉搏波信号数据的处理中可以得到较好的去噪效果，且证实了该方法可以提高信号的信噪比，并能够减小信号的均方根误差。

本文中提到的预处理方法能对后续脉搏波信号的特征提取及识别等工作提供支持，有较好的实用意义和参考价值。

[1] 罗志昌，张松，杨益民. 脉搏波的工程分析与临床应用[M]. 北京：科学出版社, 2006.

[2] 季忠,刘旭. 基于波形特征和小波的脉搏波特征点识别研究[J]. 仪器仪表学报,2016(2):379-386.

[3] MADEIRO J P V, CORTEZ P C, MARQUES J A L, et al. An innovative approach of QRS segmentation based on first-derivative, Hilbert and Wavelet Transforms[J]. Medical Engineering & Physics, 2012, 34(9): 1236-1246.

[4] 王思凯，纪静，王太松.利用GPS垂直向观测数据研究地面沉降[J].中国科技成果,2013(18): 1009-5659.

[5] DONOHO D L，JOHNSTONE I M. Ideal spatial adaptation via wavelet shrinkage [J]. Binometrika，1994，81 (3)：425-455.

[6] DONOHO D L. Denoising by soft-thresholding [J]. IEEE Transactions on Information Theory，1995，41 (3)：613-627.

[7] 姜德轩, 申涛, 王孝红. 基于小波分析的磨音信号处理[J].济南大学学报 (自然科学版), 2011, 25(3): 305-309.

[8] 朱艳芹, 杨先麟. 几种基于小波阈值去噪的改进方法[J]. 电子测试, 2008 (2): 18-22.

[9] 苑津莎, 张冬雪, 李中. 基于改进阈值法的小波去噪算法研究[J]. 华北电力大学学报, 2010, 37(5): 92-97.