期望效用函数在投资组合中的应用
(西安欧亚学院 陕西西安 710065)
一、EU理论及发展
期望效用函数理论(Expected Utility Theory)是20世纪50年代,冯·诺依曼和摩根斯坦(Von Neumann and Morgenstern)在公理化假设的基础上,运用逻辑和数学工具,建立了不确定条件下对理性人(rational actor)选择进行分析的框架。2 0 世纪中期诞生的期望效用理论(简称EU理论)将效用的分析从确定性条件或环境带入了不确定性条件或环境,成为了人们在不确定性条件或环境下的决策依据。[1]
如果某个随机变量X以概率Pi取值Xi,i=1,2,...,n,如果确定地得到Xi时的效用为u(Xi),那么,该随机变量给他的效用便是:
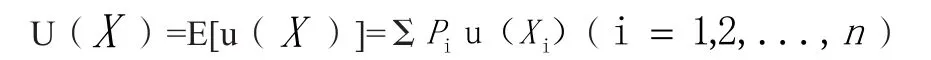
其中,E[u(X)]表示关于随机变量X的期望效用。因此U(X)称为期望效用函数,又叫做冯·诺依曼—摩根斯坦效用函数(VNM函数)。概率的效用函数表达式叫期望效用函数。
期望效用理论描述理性人在风险或不确定性环境下的消费( 投资)选择。若一个决策是在风险下做出的则意味着决策者能够列出该决策可能产生的所有后果及其相对应的可能性( 概率),风险意味着决策者对于决策结果的概率分布是已知的。
如果u(w)为一连续且二阶可导的 V N M 效用函数

为投资者在财富水平为w 时的绝对风险规避系数;

为投资者在财富水平为w 时的相对风险规避系数。
常见的效用函数有以下几种:
1.负指数效用函数u(w)=-exp(-rAw )
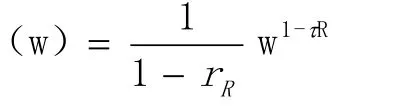
3.幂指数效用函数u(w)=-exp(-βwα),α<0,α β>0
4.对数效用函数u( w)=ln(w )

6.双曲线效用函数
二、EU理论在投资组合中的简单应用
利用期望效用理论解决投资决策问题,主要解决的是资产配置问题和收益最大化问题,通过决策优化得到预期收益。所以,作为现代资产定价理论的基石,依据EU理论建立的投资模型,在投资组合优化中具有重要的应用价值。
在经济学研究和金融投资领域,投资者追求的是自身的期望效用最大化。所以,做出最优资产组合,决策的关键是要设计一个投资比例,使其保证投资者的期望效用最大化。[2]
假如有一投资者,其投资风险行为符合对数效用函数,其拥有初始财富值为100000人民币。假定他选择两种投资产品,产品一投资x 元(产品一为风险型投资产品,比如股票),剩余资金投资产品二(为无风险的固定收益投资产品,比如国债),并获5% 的年化收益率。[3]
现考虑风险产品的单期损益情形:
情形一:
投资者的风险资产价值在一年后会增值5 0%,即变为 1.5x ;
情形二:
投资者的风险资产价值在一年后会损失30%,即变为 0 . 7x 。
在上述两种情形下投资者一年后的财富分别为
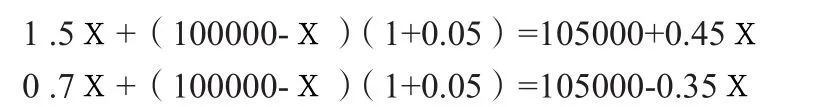
投资者诂计情形一发生的概率为0.6,情形二发生的概率为0.4
可以得出期望效用函数

要使该投资者风险资产投资份额 x 效用最大化,对上式一阶求导并令其等于0,则有
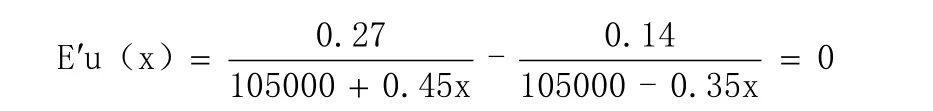
可得x≈86666.7
得到相应的期望效用E[u(x)]=11.56
这样投资者对风险型产品一,投份额为86666.7元,就可以得到效用最大化的收益。
该理论的应用前提是投资者对风险型产品的损益要有量化估计,要对产品损益情况发生的概率有所估计,这本身是一件难事。所以该理论的应用具有一定得局限性。
[1]宋立军杨永愉基于效用函数的投资组合[J].北京化工大学学报,2008,35(2):110-112.
[2]冯素芬效用函数在金融学中的应用[J].北京工业职业技术学院学报,2010,9(1):119-121.
[3]陈凯黄滋才基于期望效用与前景理论的行为决策精算定价模型[J].保险研究2017(J):56-67

